深厚软土区桩柱式桥墩临界荷载简化计算方法

刘晓明 ，李曦 ，刘齐建 ，刘涛 ，殷悦 ，曾磊

（1.湖南大学 土木工程学院，湖南 长沙，410082；2.中交公路规划设计院有限公司，北京，100088；3.广州市高速公路有限公司，广东 广州，510032）

桥梁桩基屈曲问题是桥梁设计中不可避免的关键问题之一，对于深厚软土地区尤其如此.20世纪20年代以来，学者们对桩基稳定性问题进行了大量的理论、试验和数值分析研究，得到了丰富的成果.赵明华等［1-3］基于能量法推导出桩柱式桥墩在不同边界条件下的计算长度公式，开展了室内模型箱试验验证其准确性，并提出了有限元分析桩基屈曲问题的方法.彭锡鼎［4］基于伽辽金法考虑了桩侧土抗力，推导出两端固支桩基的计算长度公式.邹新军等［5］对桩基屈曲问题引入新型无单元Galerkin 数值分析法，建立了无单元网格计算程序.雷勇等［6］依据能量法建立了穿越单层溶洞基桩总势能方程，并引入尖点突变理论，导出了分岔集方程，提出了穿越单层溶洞基桩屈曲临界荷载计算方法.但是，要将这些科研成果应用于工程，需要开发复杂的程序或软件，因此设计中往往倾向于简化方法.对于桩柱式桥墩，基于欧拉公式导出的简化计算公式［7］简单明了，是目前设计中最常用的计算方法［因其被写入《建筑桩基技术规范》（JGJ 94—2008）［8］，下文简称该方法为规范法］，但是分析表明，它在理论上存在缺陷，计算结果并不准确.

经过多年发展，基于特征值屈曲分析的有限元方法已经在结构稳定性分析中得到广泛的应用［9］，其结果也被证明与实际相符.本文拟在深厚软土区桩柱式桥墩临界荷载分析中引入特征值屈曲分析的有限元方法对桩柱式桥墩进行分析，在对比说明规范法的适用范围后，基于机器学习方法整理出简化计算公式供设计同行参考.

1 有限元法的特征值屈曲分析

1.1 计算原理

特征值屈曲分析的有限元方法是将桩身划分为若干单元，考虑每个单元所受的节点荷载、桩侧土抗力、自重、摩阻力，建立相应于该单元的桩土体系总势能方程，利用势能驻值原理，获得各单元的刚度矩阵［k］e，将单元刚度矩阵组成与桩顶荷载P有关的总刚度方程后得到：

式中：［K］为总刚度矩阵，由单元刚度矩阵［k］e组装而成；｛δ｝为结构在荷载作用下的位移；｛P｝为结构上的荷载.

式（1）中，总刚度矩阵［K］的逆矩阵等于其伴随矩阵除以系数的行列式，当总刚度系数行列式等于零时，即：

此时，位移｛δ｝将趋于无穷大，说明结构丧失了稳定性，将发生失稳破坏，故式（2）通常称为桩身屈曲稳定的有限元特征方程.求解该n阶方程可得到n个特征值，对应n阶的屈曲模态，在实际工程中，当结构的荷载达到特征值中的最小值时即发生破坏，故其中最小特征值即桩身的临界荷载Pcr.

1.2 现场试验简介

采用作者早年完成的位于洞庭湖深厚软土区的茅草街大桥超长嵌岩灌注桩屈曲试验对有限元模型进行标定.现场地质条件如表1 所示［10］，桩周土体水平抗力系数m≈5 500 kN·m-4，桩径1 m，计算宽度b1=1.8 m，混凝土等级C30，弹性模量E=31 GPa，计算可得桩土变形系数α=0.381 9 m-1.限于篇幅，试验过程不再赘述，可参阅相应文献.

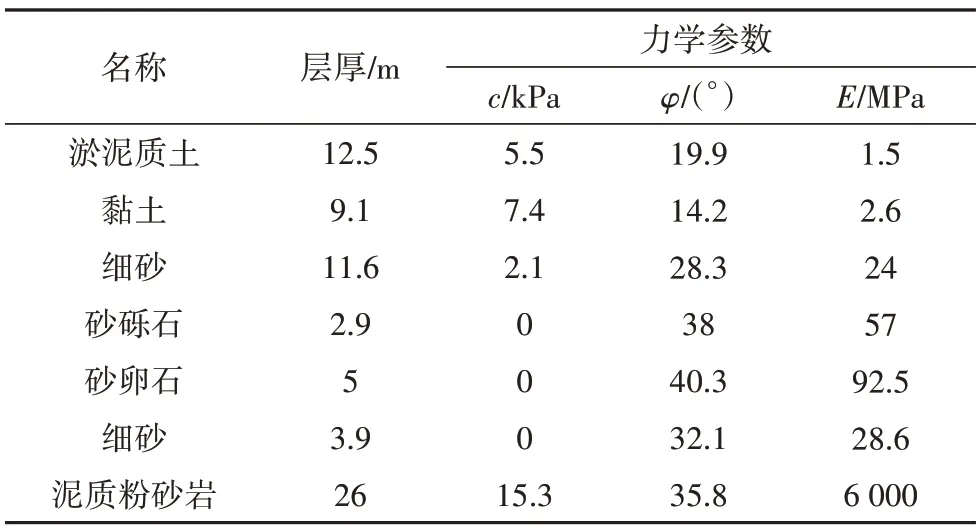
表1 桩周土层力学指标Tab.1 Soil mechanical indicators around the pile

试验加载至17 280 kN 并维持加载约5 min 时，桩身沉降突然增加，地下同时发出一声很闷的巨响，之后试桩偏位，地面出现裂缝，桩身沉降无法稳定，可判定桩身折断，其屈曲的临界荷载可取16 720 kN.

1.3 有限元计算

使用有限元软件ABAQUS 对该现场试验进行建模分析.模型采用三维可变形的C3D8R单元建立，桩基本构模型采用弹性模型，弹性模量E设为3.1 GPa；土层的本构模型采用摩尔库仑模型，具体参数取值如表1 所示.桩土之间设置接触面，法向行为设置为硬接触、切向行为设置为罚函数，摩擦系数设为0.5.土体四周及底面设置位移边界条件以约束土体位移，桩底边界条件为嵌固，桩端自由.同时为提高计算精度，将桩与桩周土体进行进一步的加密划分，模型建立如图1所示.

图1 桩-土模型示意图Fig.1 Pile-soil model schematic diagram

模型的材料属性、网格、接触属性、边界条件建立后模拟现场试验的各级加载，创建静力学功能下的geo分析步对地应力进行平衡，之后创建静力通用分析步，将荷载分级加于桩顶，得到各级荷载下桩身轴力，绘制深度-轴力曲线，并将现场试验实测数据以散点形式在图上对应位置标出，如图2 所示.图2曲线显示，现场试验实测数据点基本落于深度-轴力曲线上，说明了模型参数的正确性以及模型计算的可行性与准确性.

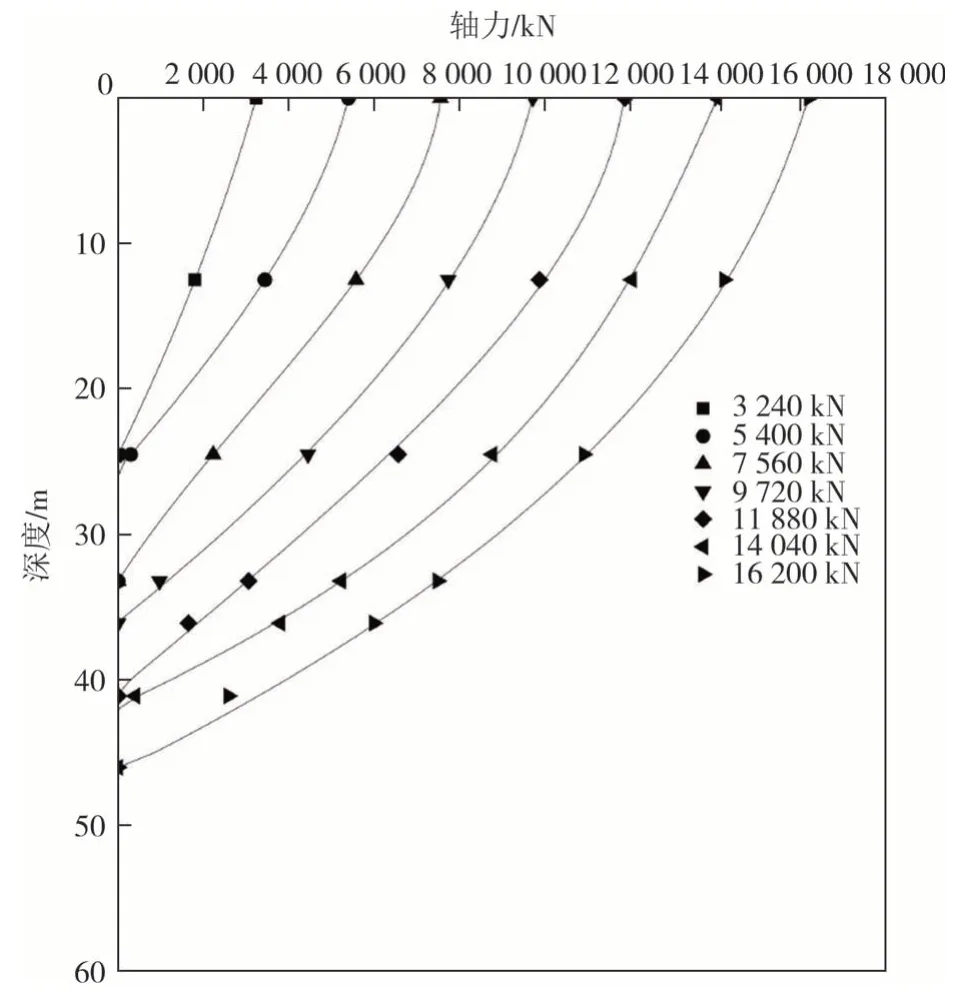
图2 深度-轴力曲线Fig.2 Depth-axial force curves

然后分析该地层条件下桩的临界荷载，创建线性摄动功能下的buckle 分析步计算桩的临界荷载，计算得其临界荷载Pcr=17 006 kN，桩发生屈曲破坏时，桩、土模态如图3所示.

图3 桩、土变形示意图Fig.3 Pile and soil deformation diagram

计算表明，采用有限元方法计算结果与现场试验实测值接近，说明有限元方法计算桩基屈曲临界荷载是可靠的.

1.4 按规范简化公式计算

常用的简化计算方法［7］（下文称：常用简化公式）过程如下：首先按式（3）确定计算长度lp的取值.

式中：l0为柱高，m；α为桩土变形系数，m-1.

然后将lp代入式（4），即可得到规范法下的临界荷载值.

式中：E为桩弹性模量，Pa；I为桩横截面极惯性矩，m4.

对于茅草街大桥试验基桩，根据式（3）可得lp=7.33 m，再根据式（4）可得临界荷载值Pcr=223 610 kN，这与实测值（Pcr=16 720 kN）相差很大，表明常用简化公式计算结果并不准确，这是因为该公式假定桩基在4/α深度处已经嵌固，故将计算长度定为柱高与嵌固深度之和再乘边界条件系数，桩嵌固深度以下的部分不受影响.事实上，不同种类土的力学性质差异很大，这一假定显然是不严谨的，因此本文将对该方法的适用范围进行研究，然后提出新的简化计算方法.

2 常用简化公式适用范围分析

2.1 数值实验方案

一般来说，深厚软土区的地层分布特点为：上层的软土层（包括淤泥、淤泥质土、流塑性黏土、软塑黏性土等），中层的硬土层（包括砂层、粉砂层、硬塑黏土层、卵石层等），下层的岩石层.图4 所示地层可代表典型深厚软土区的地层.本文基于该图所示地层研究典型软土区桥梁桩基临界荷载变化规律.

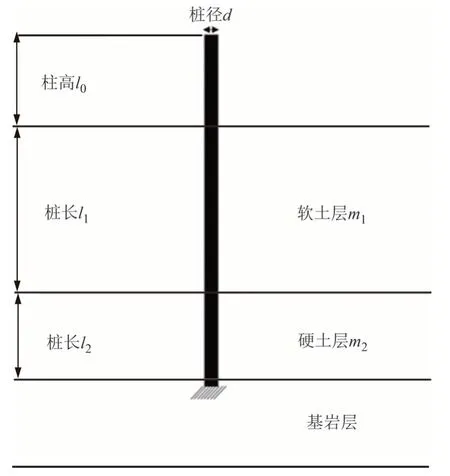
图4 模型参数示意图Fig.4 Model parameter schematic diagram

考虑对临界荷载有影响的土层水平抗力系数m值、桩径d、桩长l、柱高l0这4 种因素进行数值实验.其中，桩长l由软土层中桩长l1与硬土层中桩长l2两部分组成（l=l1+l2）；m由软土层中m1与硬土层中m2两部分组成.改变各参数的取值水平，分别采用常用简化公式法和基于特征值分析的有限元法计算各参数组合下桩柱式桥墩临界荷载值，模型参数示意图如图4 所示.模型中各参数取值范围如表2 所示，计算时将各个因素取不同水平组合进行计算.

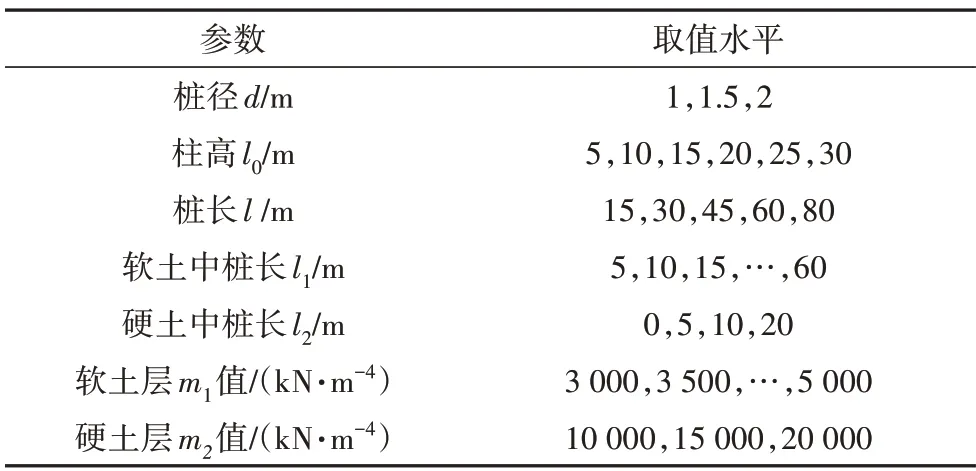
表2 参数取值Tab.2 Parameter values

由于有限元软件中没有直接定义土的水平抗力系数的参数，故需要将土层水平抗力系数m值与弹性模量E值进行换算，其方法为将有限元软件各弹性模量下桩的水平载荷试验产生的桩顶水平位移与规范法各m值下计算的桩顶水平位移进行对比，将计算结果非常接近的弹性模量E与m值对应起来，形成若干组数据，运用最小二乘法进行回归分析，以得到弹性模量E与m值的对应关系［11］，本文模型将桩周土层简化为单层土，这样能将土层参数与某一确定m值对应起来，本文中m值与弹性模量E的对应关系如表3所示.

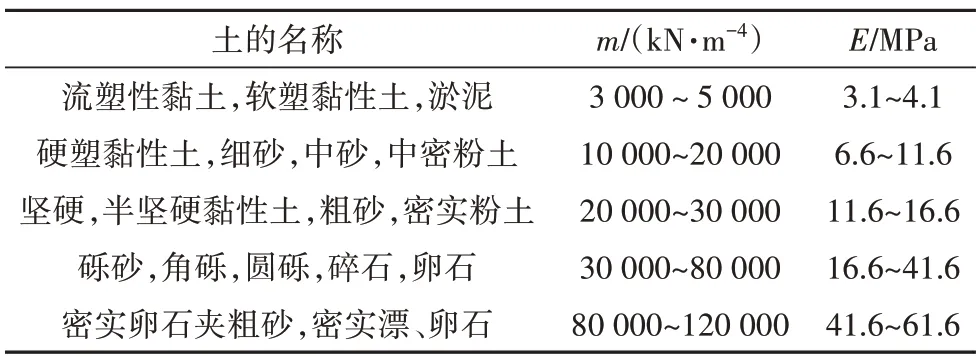
表3 m与E对应取值Tab.3 Corresponding values between m and E

2.2 计算结果分析

将相同参数组合下，两种不同方法计算所得临界荷载绘制成散点图（规范法Pcrs-有限元法Pcra），如图5所示（长细比=l1/d+l2/d）.

图5 规范法Pcrs-有限元法Pcra计算结果Fig.5 Results between code method Pcrs and FEM Pcra

计算结果显示，长细比为7.5～20时，两种方法的计算结果接近；长细比为20～45 时，两种方法的计算结果已经较为接近；长细比为60～45 时，两种方法的计算结果偏差很大.这说明随着桩长细比的增大，规范法计算结果与有限元计算的结果偏差越来越大，故需要对规范法的计算公式进行修正.

3 临界荷载简化计算公式

3.1 随机森林算法简介

近年来，人工智能发展迅速，机器学习逐渐应用到越来越多的专业领域，其中随机森林算法（Random Forest）对于数据的适应能力强，实现方法较为简便，被广泛地应用于数据处理当中.随机森林是一种可用于回归分析的非参数集成学习算法［12］，起源于对于决策树的研究［13-14］，通过随机选择训练样本与特征变量的方法生成多个CART 决策树［15］，之后通过投票计分的方式将这些决策树的训练结果结合起来，以获得最终的回归模型，训练好的模型将可以通过输入自变量参数，较为准确地预测出因变量参数.

评价随机森林模型的回归效果，可采用平均绝对值误差（MAE）、平均均方根误差（RMSE）和拟合优度（R2）这3个评价指标［13］，本文采取拟合优度（R2）指标进行评价.评估方法采用“留出法”，将用有限元方法计算出来的数据划分为两个数据集合，把其中一个集合作为训练集S，另一个作为测试集T，在训练集S上训练好模型之后，再在测试集T上评估其预测精度，若两个集合的预测精度均在0.99以上，则说明模型训练效果较好，模型预测精度较高.

3.2 随机森林模型预测结果

为得到深厚软土区桩柱式桥墩计算长度的简化公式，以第2 节中的数值模型的计算结果为基础，将结果换算为计算长度，与输入参数构成数据集.随机选取数据集66.7%的数据作为训练集S，33.3%的数据作为测试集T［16］，以长细比、柱高、桩土变形系数α值、土层水平抗力系数m值作为输入特征变量，采用随机森林回归算法对计算长度进行预测.将随机森林模型得到的预测值与有限元法的计算值绘制散点图，如图6所示.

图6 随机森林模型预测值与有限元计算值比较Fig.6 Comparison of predicted values from random forest model and FEM calculations

结果显示，训练集与测试集的计算结果均处于1∶1 线附近，测试集的拟合优度也达到了0.99 以上，深度学习的效果非常好，证明输入参数与输出参数之间具有很强的相关性，可使用公式的形式对其进行拟合.

3.3 基于随机森林模型的计算长度简化公式

对于随机森林模型，根据Gini 指数计算特征变量，可分析各个属性的重要性［15］，以各因素的重要性指数为基础可以确定拟合公式中参数的形式从而导出公式.计算本文随机森林模型中各特征的重要性，并绘制柱状图如图7所示.

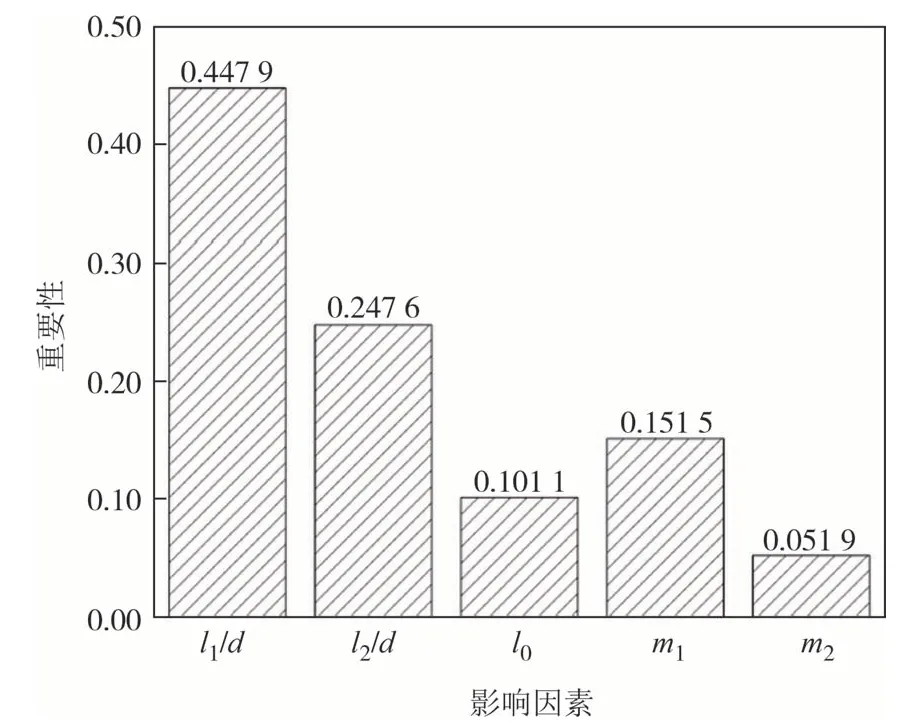
图7 各影响因素重要性Fig.7 Importance of each influencing factor

计算结果显示，在深厚软土区的桩柱式桥墩的稳定性问题中，桩的长细比对于计算长度的影响占主导地位，其中软土层中桩长细比l1/d占44.79%，硬土层中桩长细比l2/d占24.76%，合计69.55%.m值的影响次之，其中软土层m1占15.15%，硬土层m2占5.19%，合计20.34%.柱高l0对计算长度也有一定的影响，占10.11%；因此以式（3）为基本形式，纳入l/d参数可得到更准确的简化计算公式.本文采用不同形式的公式进行分析，得到桩柱式桥墩计算长度简化公式如（5）所示，将拟合结果绘制在图8 中，可见计算较好.

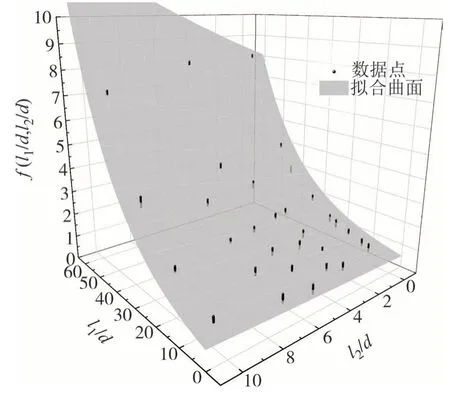
图8 拟合曲面Fig.8 Fitted surface

根据式（5）计算各参数水平下计算长度，然后采用式（4）计算桩柱式桥墩的临界荷载，再与有限元法计算值比较，绘制散点图（2 520 个数据点）如图9所示.

图9 修正公式预测值与有限元计算值比较Fig.9 Comparison of predicted values from modified formula and FEM calculations

计算结果表明，本文提出的简化计算方法效果良好，具有实用价值.

4 结论

本文分别采用基于特征值屈曲分析的有限元数值软件法、规范法，对桩柱式桥墩的屈曲临界荷载进行计算和比较，并使用随机森林法对有限元计算结果进行分析，得到结论如下：

1）采用有限元数值软件方法计算桩柱式桥墩的临界荷载，其计算结果与现场试验结果较为吻合，说明基于特征值屈曲分析的有限元法对桩柱式桥墩的临界荷载计算是适用的.

2）现有常用简化计算方法在桩的长细比较大、时计算结果误差较大，适用性差.

3）基于有限元计算以及随机森林回归分析，拟合得到了深厚软土区桩柱式桥墩的临界荷载计算简化方法，可供设计人员使用与参考.