四主缆大跨悬索桥抗震性能分析及减震措施优化

刘志文 ，魏祎博 ，王连华 ，丁少凌 ，谢功元 ，谢学鑫 ，陈政清

（1.湖南大学 桥梁工程安全与韧性全国重点实验室，湖南 长沙 410082；2.湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082；3.湖南大学 土木工程学院，湖南 长沙 410082；4.中交第二公路勘察设计研究院有限公司，湖北 武汉 430212；5.湖北交投宜昌高速公路建设管理有限公司，湖北 宜昌 443000）

地震是人类面临的最危险的自然灾害之一.大跨桥梁在地震作用下遭受严重破坏后会造成巨大的经济损失，因此各国对桥梁结构抗震性能要求逐渐提高［1］.悬索桥凭借其卓越的跨越能力及优美的外观，逐渐成为大跨桥梁的首选桥型之一，学者们对悬索桥抗震性能和控制措施已做大量研究［2］.

对于悬索桥抗震性能研究大多采用反应谱和时程分析法，McDaniel 等［3］对新建旧金山-奥克兰海湾大桥进行了地震时程响应分析，发现地震作用下桥塔中部产生较大弯矩和位移.邓育林等［4］分析了泰州长江公路大桥抗震性能，发现纵向地震作用下主塔的最大位移出现在离塔顶约 1/4 塔高处.王德华［5］在博斯普鲁斯大桥的抗震性能研究中发现地震作用下主桥梁端产生1.078 m 的纵向位移，有可能会对伸缩缝造成损伤.刘长喜［6］也在刘家峡大桥抗震性能分析中发现大跨径悬索桥对纵向地震激励的地震反应较大的现象.综合上述研究，不同形式、不同跨径的悬索桥地震响应不同.在建燕矶长江大桥由于塔高受当地航空限高影响，采取了不同垂度四主缆悬索桥方案设计［7］，从抗震性能和工程设计角度而言，四主缆大跨悬索桥与常规双主缆悬索桥理论上存在较明显的差别，显然需要进一步深入研究以满足这种桥型的抗震设计需求.

地震荷载作用下，悬索桥梁端纵向位移过大，可能造成伸缩缝破坏、梁与相邻引桥之间的撞击等问题［8］，需采取控制措施抑制梁的过大纵向位移，提升桥梁抗震性能.大跨悬索桥控制措施有增设中央扣［9］、塔梁弹性连接装置［10］及阻尼器［11］等方式，其中湖南大学陈政清院士发明的大吨位新型电涡流轴向阻尼器，具有稳定性好、耐久性好、维护要求低等优点［12］，已成功应用于杭瑞高速岳阳洞庭湖大桥减震控制中［13］.Zhang 等［14］通过对比分析电涡流阻尼器和传统黏滞阻尼器的阻尼性能，发现电涡流阻尼器表现出良好的减震性能，可实现对典型黏滞阻尼等效取代.杨孟刚等［15］对某主跨为350 m 的独塔自锚式悬索桥进行减震控制研究，发现采用磁流变阻尼器能够有效地减小悬索桥的纵向地震响应，并在之后平胜大桥的减震研究中，通过地震模拟振动台试验验证了电涡流阻尼器能达到较好的悬索桥纵向地震反应减振效果［16］.已有研究主要针对常规轴向电涡流阻尼器，张弘毅等［17］在此基础上提出了一种兼顾桥梁准静态振动和一般振动的电涡流-摩擦组合型阻尼器，但目前对该新型组合型阻尼器的减震性能以及地震作用下阻尼器内部电涡流阻尼力和摩擦力的减震特点研究较少.

综上所述，本文以在建燕矶长江大桥为工程背景，采用SAP2000 软件建立该桥有限元模型，基于非线性时程法对该桥开展抗震性能研究，对比分析电涡流-摩擦组合型阻尼器和黏滞阻尼器参数优化结果，并研究电涡流-摩擦组合型阻尼器在地震作用下的减震特点.

1 工程概况

燕矶长江大桥地处湖北省黄冈市和鄂州市交界处，是一座跨径布置为（550+1 860+450）m 的单跨双层四主缆钢桁梁悬索桥.主缆由平行钢丝索股组成，采用四缆不同矢跨比设计，内主缆垂跨比为1/13.058，横向间距35 m；外主缆垂跨比为1/12.130，横向间距41 m，单侧两主缆中心间距3 m，内外主缆均采用127 根直径5.6 mm 的高强度镀锌-铝钢丝组成，每根通长索股有217 股.内外吊索间距9.0 m 交错布置，其中内主缆吊索全部采用单丝直径5 mm、共151 丝的高强平行钢丝吊索，外主缆跨中11 根吊索采用直径90 mm 的不锈钢钢拉杆，其余均为单丝直径5 mm、共151丝的高强平行钢丝吊索.主桁架为华伦式桁架结构，桁高9.5 m，标准节间长9 m，2片主桁中心间距35 m，并分别在两侧梁端设有4 个横向抗风支座.主塔采用2根塔柱和2道横梁组成的钢筋混凝土门式框架结构，其中黄冈侧主塔高200.3 m，鄂州侧主塔高189.3 m，均采用群桩基础.采用正交异性钢桥面板，上层为双向6 车道，下层为双向4 车道，其中下桥面板中央开槽3 m 以提升主桥抗风性能（注：加劲梁下层桥面最终方案采用全封闭），燕矶长江大桥总体布置如图1所示.

2 结构动力特性分析

2.1 模型建立

采用大型有限元软件SAP2000 建立燕矶长江大桥有限元模型，有限元模型截面参数如表1 所示.主塔与桁架加劲梁采用空间梁单元模拟，主缆、吊索采用空间桁架单元模拟，并折减框架单元抗弯刚度，折减系数取0.01，同时释放单元两端弯矩以保证缆索单元仅受轴力并施加P-Δ力考虑垂度效应和恒载引起的几何刚度影响，其中缆索单元P-Δ力通过恒荷载工况计算得到.桥塔承台底部采用6×6 集中土弹簧模拟桩土相互作用，弹簧刚度根据土层m值计算；主缆锚固点固结，塔顶与主缆连接处耦合所有平动自由度，未考虑主缆在塔顶鞍座的纵向移动，塔梁连接处耦合横桥向自由度.增设组合型阻尼器后大桥有限元模型如图2所示.

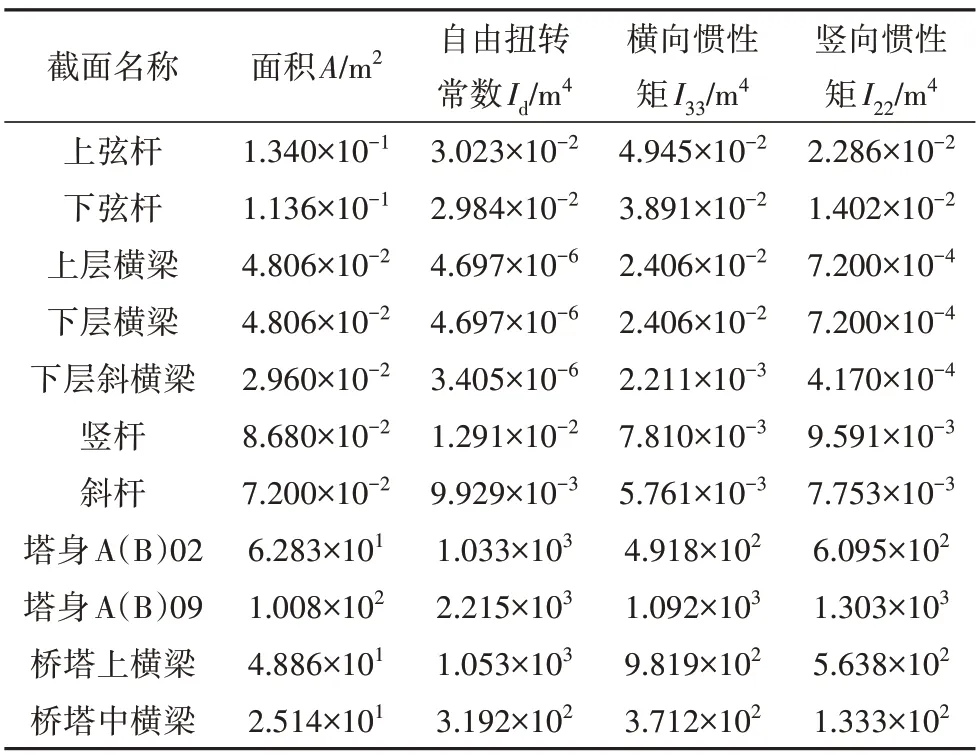
表1 有限元模型截面参数Tab.1 Section parameters of finite element model

图2 燕矶长江大桥有限元模型Fig.2 Finite element model of Yanji Yangtze River Bridge

2.2 分析结果

采用Ritz 向量法计算桥梁前600 阶固有频率和周期，图3 所示为燕矶长江大桥主桥结构前10 阶自振特性计算结果.加劲梁一阶正对称侧弯频率为0.046 6 Hz，对应周期为21.45 s；加劲梁一阶反对称竖弯频率为0.090 4 Hz，对应周期为11.06 s.

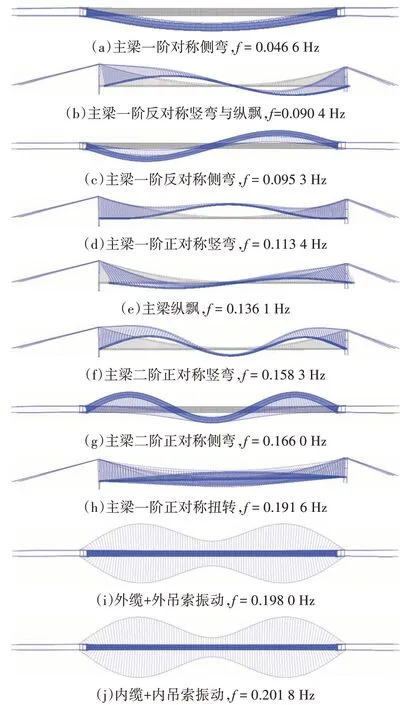
图3 燕矶长江大桥主桥成桥状态前10阶振型图Fig.3 The first ten order mode shapes of Yanji Yangtze River Bridge in service stage

3 主桥结构抗震性能分析

3.1 地震动输入

根据桥位区地震环境及《燕矶长江大桥工程场地地震安全性评估报告》给出的不同概率水平下的地震动参数，选取阻尼比为2%，50年超越概率2%水平向的三条人工地震波进行非线性时程分析，竖向加速度值取水平向的65%，图4给出了水平向设计地震动时程曲线，峰值地面加速度为154.2 cm/s2.考虑到燕矶长江大桥为长周期大跨径悬索桥，《燕矶长江大桥工程场地地震安全性评估报告》将设计加速度反应谱周期范围扩展至22 s，上述3条人工时程地震波的反应谱与安评报告中设计反应谱对比如图5 所示，除周期较大的区域反应谱曲线存在轻微差别，其余区域吻合较好.

图4 桥位处水平向地震加速度时程Fig.4 Horizontal seismic acceleration time history

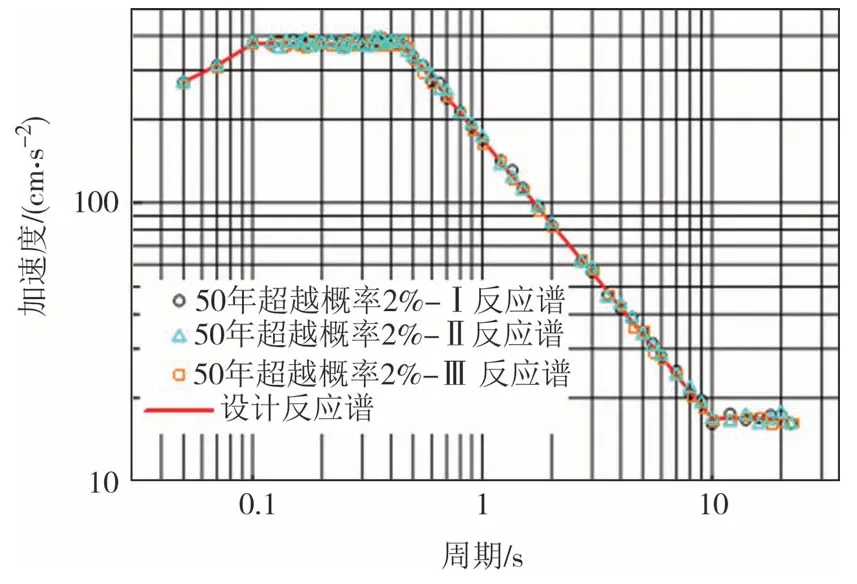
图5 时程曲线的反应谱与设计反应谱Fig.5 Time-history curve response spectrum and design response spectrum

3.2 非线性响应分析结果与验算

根据《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）确定燕矶长江大桥为A 类桥梁，设防目标为：1）E1 地震作用下，主塔、桩基保持弹性，基本无损伤，弯矩地震响应小于初始屈服弯矩；2）E2 地震作用下，主塔、桩基基本保持弹性，混凝土保护层不脱落，不需修复或经简单修复可正常使用，弯矩地震响应小于等效屈服弯矩.

3.2.1 地震响应结果

在50 年超越概率2%地震作用沿“纵向+竖向”和“横向+竖向”方向输入下，主桥关键节点最不利位移响应如表2所示，表中正位移方向与图2有限元模型坐标系正方向相同.图6 所示为“纵向+竖向”地震组合E2 地震作用下黄冈侧梁端纵向位移时程曲线，图7所示为“纵向+竖向”及“横向+竖向”地震组合E2地震作用下黄冈侧塔底弯矩时程曲线.

表2 E2地震作用下主桥关键节点位移Tab.2 Critical nodes displacement of YJB under E2 earthquakes cm

图6 黄冈侧梁端纵向位移时程曲线（“纵向+竖向”地震）Fig.6 The longitudinal displacement time history curves of the Huanggang side stiffening girder end（longitudinal and vertical seismic acceleration）

图7 黄冈侧桥塔内力响应时程曲线Fig.7 Time history curves of intern force of the Huanggang side tower

通过梁端纵向位移时程曲线可以直观表征出地震过程中梁端纵向运动特点，地震发生起始阶段，由于结构惯性存在，吸收地震能量大部分转化为结构加速度，梁端开始运动，随地震能量输入，梁端纵向位移在地震发生64.56 s 达到峰值，之后地震动能量输入减少直至结束，梁端纵向位移响应通过结构自身阻尼等耗能缓慢衰减.地震作用下，梁端存在较大的纵向位移，易引起伸缩缝破坏，需采取减震措施进行控制.

通过E2 地震作用下桥塔内力响应时程曲线可以看出，在“纵向+竖向”和“横向+竖向”地震输入时，塔底均存在较大的弯矩响应，需对桥塔截面进行内力验算.

3.2.2 桥塔截面验算

采用XTRACT 软件，按照纤维单元法对主桥主塔在永久作用和地震作用下的最不利轴力组合进行轴力-弯矩-曲率分析，可以得到各关键截面的初始抗弯屈服强度M'y、等效抗弯屈服强度My、极限抗弯屈服强度Mu，并以此进行结构抗震性能验算.

表3 和表4 分别为“纵向+竖向”地震组合和“横向+竖向”地震组合E2 地震作用下桥塔上横梁对应塔柱截面［AB（02）］、中横梁对应塔柱截面［AB（06）］、塔底截面［AB（11）］以及上横梁截面、中横梁截面抗弯能力验算结果.

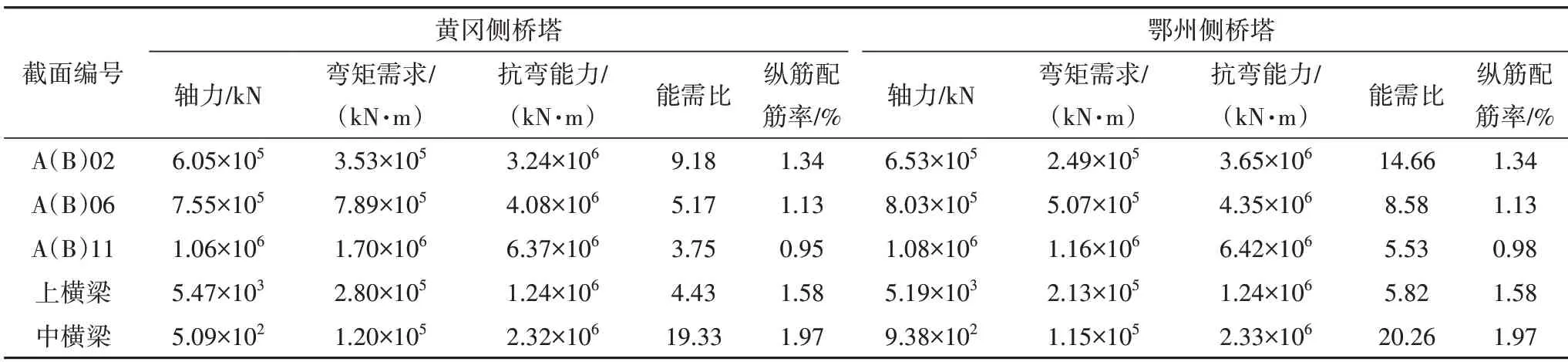
表3 E2地震作用下桥塔关键截面抗弯验算（“纵向+竖向”地震）Tab.3 Anti-bending calculation of critical sections of the tower under E2 earthquakes（longitudinal and vertical earthquakes）

表4 E2地震作用下桥塔关键截面抗弯验算（“横向+竖向”地震）Tab.4 Anti-bending calculation of critical sections of the tower under E2 earthquakes（transverse and vertical earthquakes）

由表3、表4 可知，在E2 地震不同方向输入组合的作用下，各关键截面的抗弯能力可满足预期的性能目标.其中“纵向+竖向”地震输入时，桥塔各截面能需比均较大，而“横向+竖向”地震输入时，桥塔横梁弯矩需求显著增加.燕矶长江大桥上横梁跨径46.1 m，中横梁跨径47.0 m，属于宽幅悬索桥，横梁设计需充分考虑横向地震作用［18］.为提升横梁抗震性能，设计在横梁中增设预应力钢束，提高截面配筋率以提升截面抗弯抗剪能力，同时可起到延迟构件开裂的作用.

3.2.3 地震作用下主缆受力分析

燕矶长江大桥“纵向+竖向”地震和“横向+竖向”地震作用下内主缆及外主缆应力增量幅值如图8 所示.地震作用下内外主缆应力增量幅值相近，而在“纵向+竖向”地震作用下，受塔顶鞍座纵向摩擦力影响，边跨主缆应力增量在塔顶处发生突变.

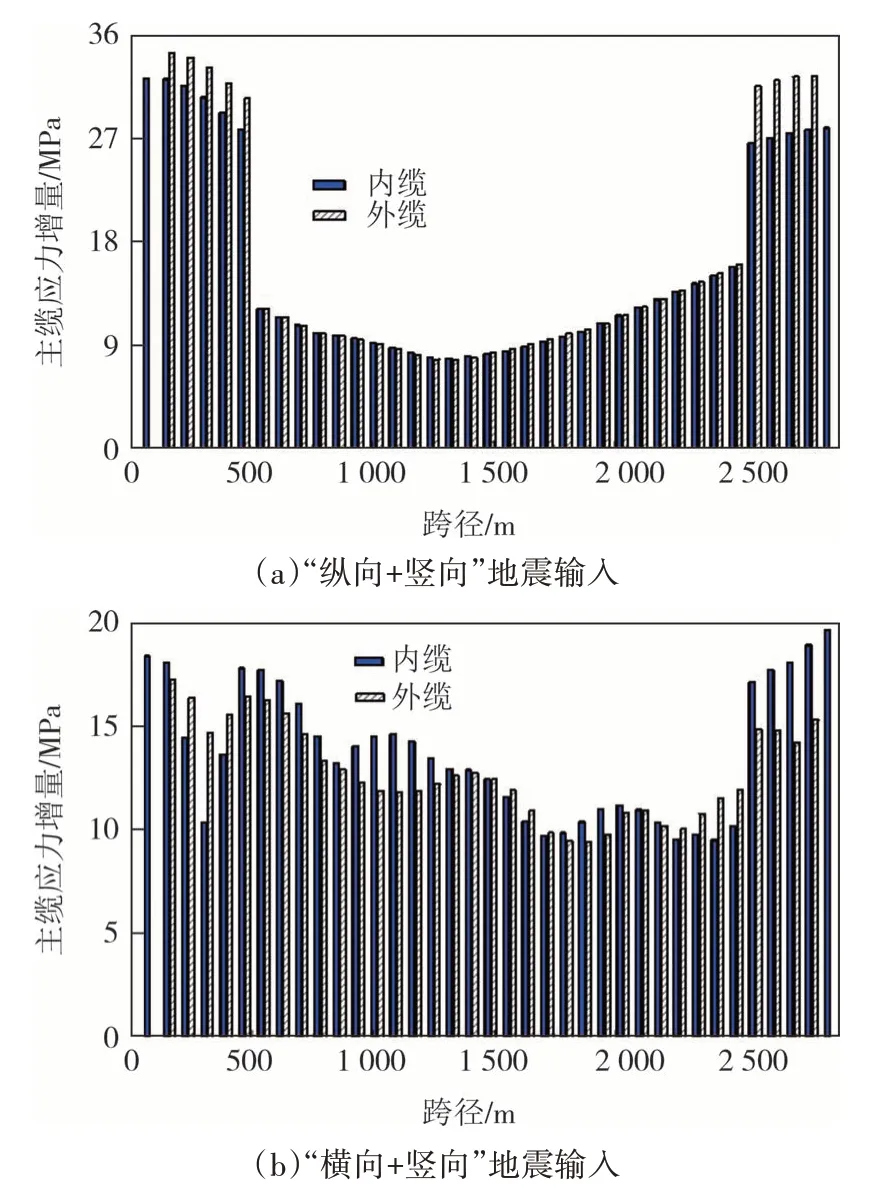
图8 地震作用下内外侧主缆应力对比Fig.8 Stress comparison of inner and outer main cables under earthquake

图9 所示为恒载作用内外侧主缆应力图，恒载作用下桥塔处主缆应力最大，跨中处主缆应力最小，对于不同垂度四主缆悬索桥，由于其内主缆垂跨小于外主缆，所以其应力略大于外主缆.结合图8 地震作用下内外侧主缆应力，发现与恒载引起的主缆应力相比，地震作用引起的额外应力较小.

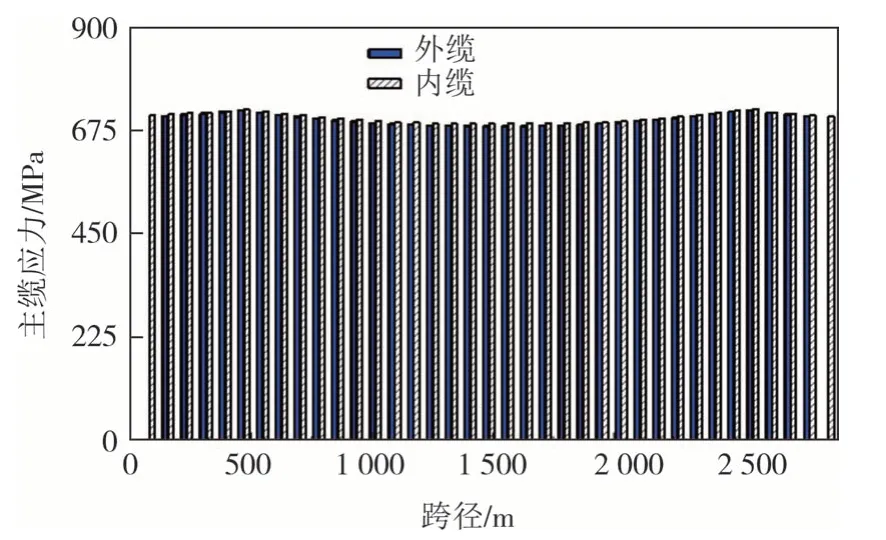
图9 恒载作用内外侧主缆应力对比Fig.9 Stress comparison of inner and outer main cables under dead load

4 减震措施优化分析

4.1 组合型阻尼器

为有效控制地震作用下加劲梁梁端纵向位移，改善桥梁在地震作用下的响应，采用湖南大学陈政清院士团队研发的电涡流-摩擦组合型阻尼器进行地震响应减震措施效果研究［17］.该新型组合型阻尼器在电涡流阻尼器的基础上增设了用于控制梁端准静态振动的摩擦预紧组件，其结构构造如图10所示.

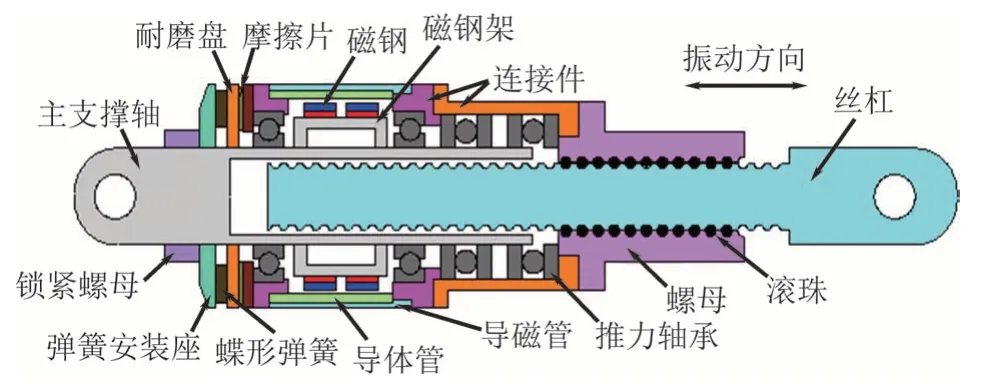
图10 电涡流-摩擦组合型阻尼器示意图［17］Fig.10 Diagram of eddy current-friction combined damper

电涡流阻尼在低速时可以视为一种理想的线性黏滞阻尼［19］，采用非线性连接单元Damper-Exponential 模拟纵向电涡流阻尼力，其阻尼力与速度关系式为：

式中：Fc为阻尼力，kN；C为电涡流阻尼系数，kN·s/m；ν为阻尼器连接两端相对速度，m/s；α为阻尼指数，电涡流阻尼器取α=1.

从工程角度讲，阻尼器减震性能可利用滞回曲线定量进行评估，为分析不同参数对滞回曲线的影响，考虑正弦激励：u(t)=u0sin(ωt)，其中u0为幅值，ω为频率.阻尼器阻尼力可以表示为：Fc=C[u0ωcos(ωt)]α，因此得到滞回曲线方程：

抗震工程中非线性黏滞阻尼器α常取0.2～1，ω=1 rad/s，对比电涡流阻尼力与非线性黏滞阻尼力滞回曲线如图11所示.

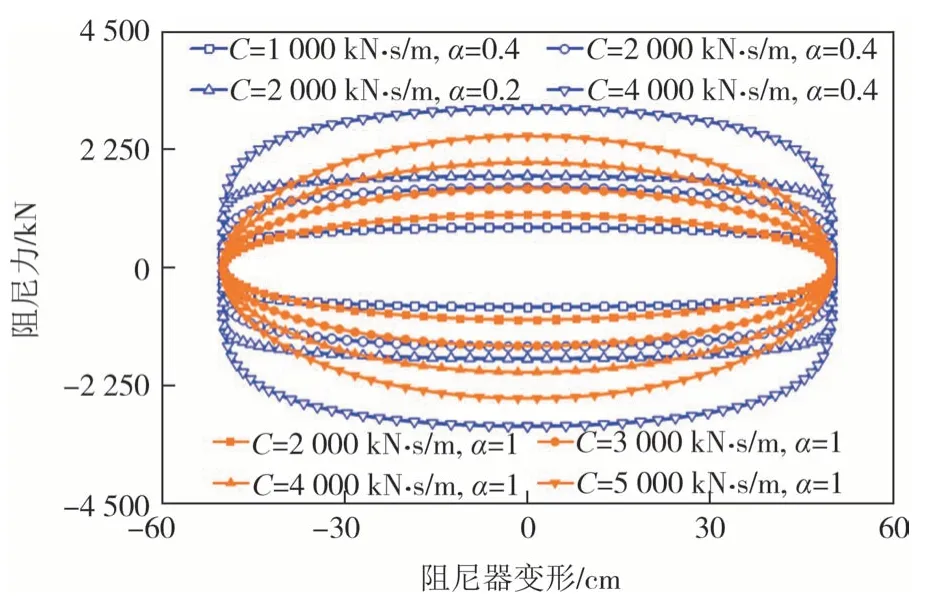
图11 电涡流阻尼力与黏滞阻尼力滞回曲线对比Fig.11 Comparison of hysteretic curves of eddy current damping force and viscous damping force

从图11 可以看出，电涡流阻尼力滞回曲线均为椭圆曲线，而黏滞阻尼器阻尼力与阻尼器两端相对速度呈非线性关系，其滞回曲线也为非线性.滞回曲线面积为阻尼器耗能，增大阻尼系数，降低阻尼指数均可增大阻尼力，增加耗能.其中，电涡流阻尼力和黏滞阻尼力均采用非线性连接单元Damper-Exponential单元模拟.

电涡流-摩擦组合型阻尼器的摩擦阻尼力与速度无关，碟形弹簧组对摩擦片施加可调且恒定的预紧压力，使阻尼器工作过程中摩擦阻力可基本保持稳定不变，摩擦力采用非线性连接单元Plastic-WEN模拟，其滞回曲线如图12 所示.另一方面，电涡流-摩擦组合型阻尼器工作过程中电涡流阻尼力与速度成正比，所以该阻尼器本构模型接近双线性，表达式为：

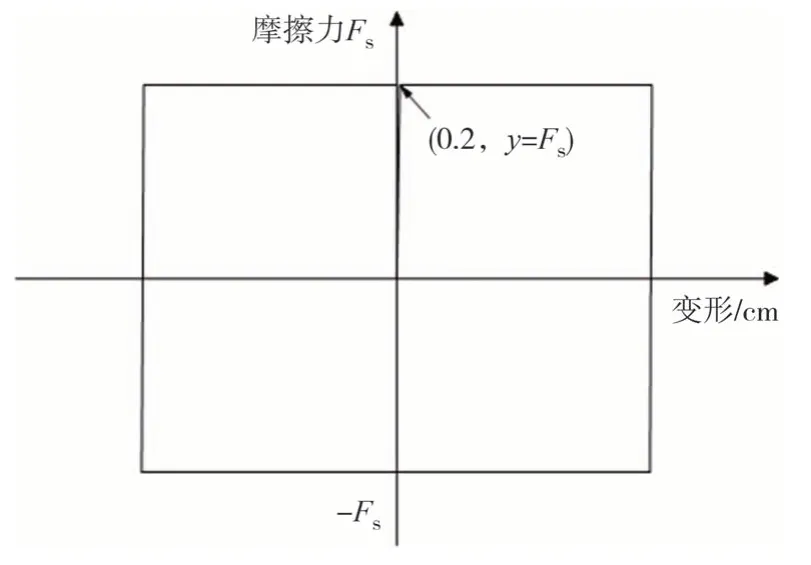
图12 摩擦力的滞回曲线模型Fig.12 Hysteretic curve model of friction force

4.2 参数优化分析

4.2.1 电涡流阻尼系数和摩擦力确定

燕矶长江大桥阻尼器纵向布置在梁端与牛腿之间，考虑到减震效果和牛腿构造要求，确定单个阻尼器阻尼力范围为800～1 600 kN.结合电涡流-摩擦组合型阻尼器电涡流阻尼和摩擦阻尼组合减震特点，地震作用下以电涡流阻尼抑震为主，电涡流阻尼力占比需达到最大阻尼力70%～90%.根据以上条件，初拟电涡流阻尼系数C和摩擦力Fs如表5 所示.同时为进行电涡流-摩擦组合型阻尼器与黏滞阻尼器的对比研究，选取阻尼指数α为0.2、0.3、0.4 和0.5 进行计算.

表5 电涡流-摩擦组合型阻尼器与黏滞阻尼器参数Tab.5 Parameters of EC-FCD and VD

计算得到上述阻尼器参数对应阻尼力峰值如图13 和图14 所示，电涡流-摩擦组合型阻尼器电涡流阻尼力和摩擦力占比如图15 所示.对于电涡流-摩擦组合型阻尼器，电涡流阻尼力与电涡流阻尼系数呈近似线性增长关系.摩擦力不变，电涡流阻尼系数增加，电涡流阻尼力占比增加，同时摩擦力占比减小.随摩擦力增大，若阻尼系数过小会导致电涡流阻尼力占比减小，阻尼系数过大会导致总阻尼力过大，致使满足设计要求的电涡流阻尼系数范围减小.

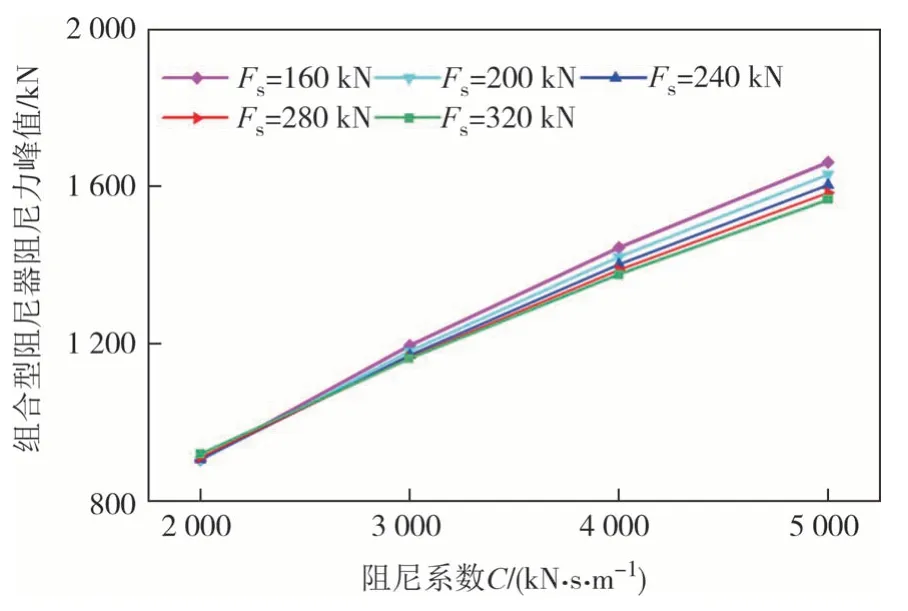
图13 组合型阻尼器阻尼力峰值Fig.13 Peak damping force of combined damper

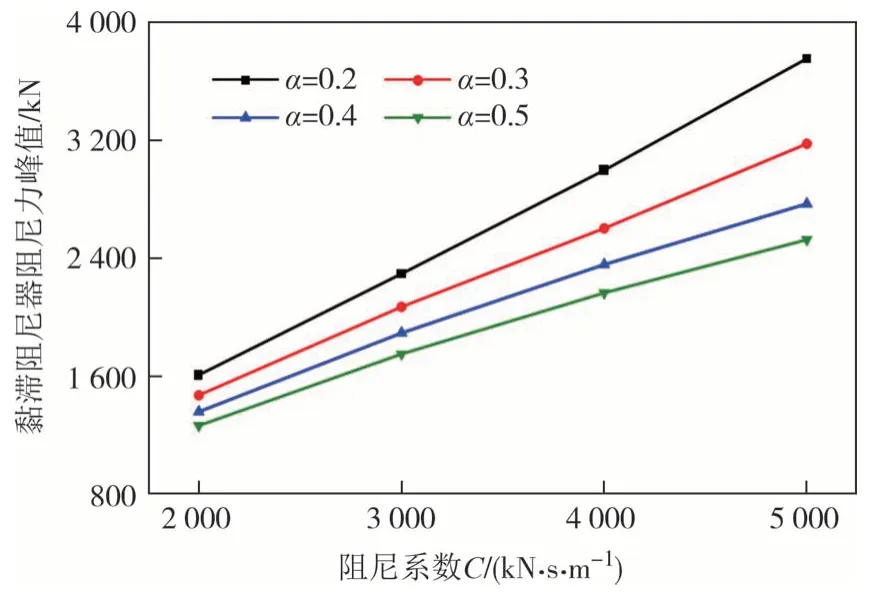
图14 黏滞阻尼器阻尼力峰值Fig.14 Peak damping force of viscous damper

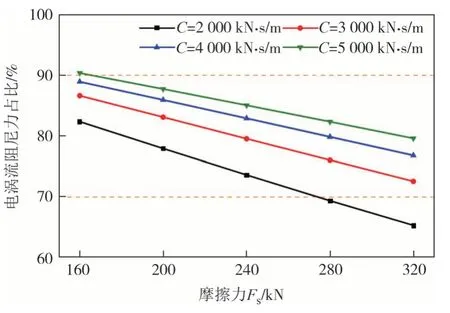
图15 摩擦力与电涡流阻尼力占比图Fig.15 Proportion of friction and eddy current damping force

对比电涡流-摩擦组合型阻尼器与黏滞阻尼器阻尼力峰值发现，黏滞阻尼器阻尼力对阻尼系数敏感性较高.同一阻尼系数，黏滞阻尼器阻尼力明显大于电涡流-摩擦组合型阻尼器阻尼力，可达到电涡流-摩擦组合型阻尼器阻尼力的1.2～2.4倍.

4.2.2 梁端纵向位移响应控制效果

图16和图17分别给出了电涡流-摩擦组合型阻尼器和黏滞阻尼器不同参数对应主桥黄冈侧梁端纵向位移图.对于电涡流-摩擦组合型阻尼器，摩擦力和阻尼系数越大，控制效果越好，摩擦力取320 kN，阻尼系数取5 000 kN·s/m 时控制效果最好，梁端纵向位移减少了76.6%，此时阻尼器达到阻尼力峰值时，摩擦力占比20%，电涡流阻尼力占比80%.

图16 黄冈侧梁端纵向位移（组合型阻尼器）Fig.16 Longitudinal displacement at the Huanggang side beam end of combined damper

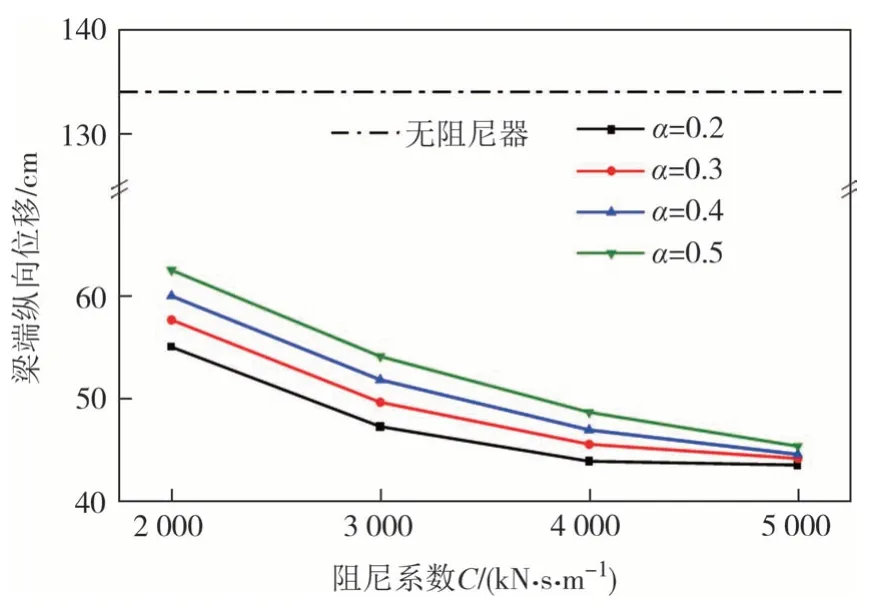
图17 黄冈侧梁端纵向位移（黏滞阻尼器）Fig.17 Longitudinal displacement at the Huanggang side beam end of viscous damper

而对于黏滞阻尼器，降低阻尼指数，增加阻尼系数均可提升阻尼器对梁端纵向位移的控制效果，但随阻尼系数增加，降低阻尼指数对梁端纵向位移控制效果提升并不显著.整体来看，电涡流-摩擦组合型阻尼器对梁端纵向位移控制效果更好.

4.2.3 桥塔塔底内力响应控制效果

图18 给出了阻尼器参数对黄冈侧和鄂州侧塔底弯矩峰值的影响.

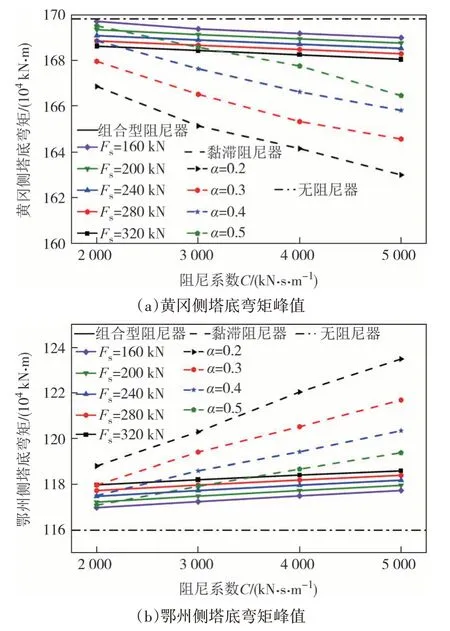
图18 桥塔塔底弯矩响应Fig.18 Bottom bending moment of bridge towers

综合两种阻尼器计算结果，黄冈侧塔底弯矩峰值最大变化了3.90%，鄂州侧塔底弯矩峰值最大变化了6.46%，塔底弯矩对阻尼器参数并不敏感.其原因是塔底的弯矩主要和主缆质量和桥塔质量、高度有关，以黄冈侧桥塔为例，黄冈侧塔顶距塔底185.0 m，阻尼器与桥塔连接处距塔底34.0 m，在同一地震作用下，主缆引起塔顶截面剪力、阻尼器产生的阻尼力和塔底弯矩时程曲线如图19 所示，地震作用下塔底弯矩时程曲线与塔顶剪力时程曲线波动一致，塔底弯矩达到最大值时，主缆对塔顶的剪力远大于阻尼力，塔底弯矩主要与主缆引起的塔顶剪力有关.

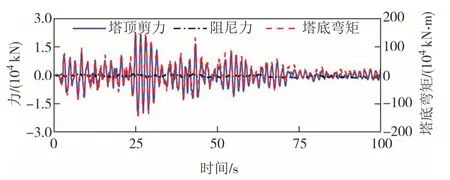
图19 塔顶剪力、阻尼力和塔底弯矩时程曲线Fig.19 Time-history curves of tower top shear，damping force and tower bottom bending moment

4.2.4 阻尼器滞回曲线与耗能

电涡流-摩擦组合型阻尼器通过电涡流阻尼力和摩擦力提供阻尼耗能，黏滞阻尼器通过液体的黏性提供阻尼耗能，两种耗能方式均能达到减弱结构振动的目的.阻尼器耗能可以通过滞回曲线体现，滞回曲线越饱满，其耗能越多，减震效果越显著.图20所示为电涡流阻尼系数C=4 000 kN·s/m 时对应不同摩擦力滞回曲线，图21 所示为摩擦力Fs=240 kN 时对应不同电涡流阻尼力滞回曲线，图22 所示为黏滞阻尼器阻尼系数C=2 000 kN·s/m 时对应不同阻尼指数的滞回曲线.

图20 摩擦力滞回曲线（C=4 000 kN·s·m-1）Fig.20 Hysteretic curves of friction force（C=4 000 kN·s·m-1）

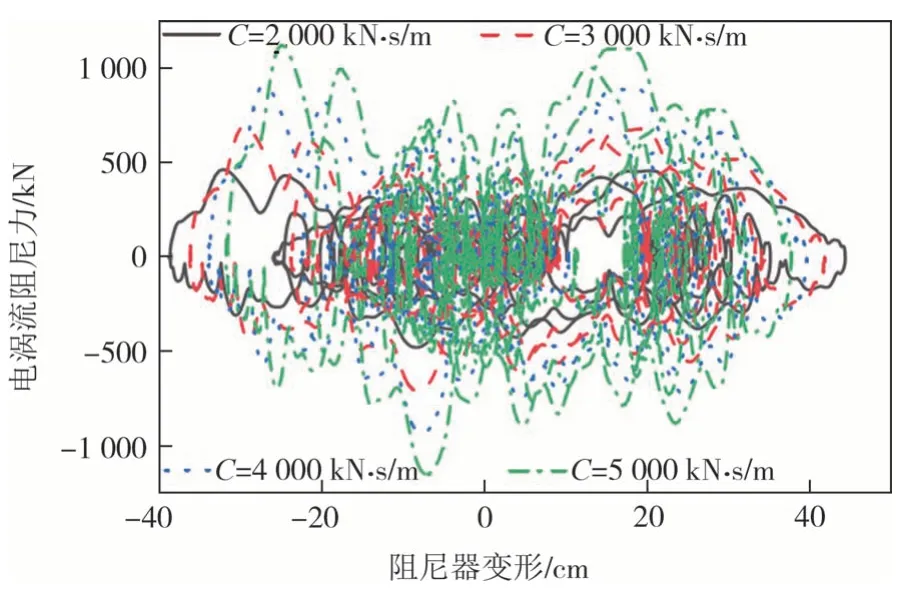
图21 电涡流阻尼力滞回曲线（Fs=240 kN）Fig.21 Hysteretic curves of eddy current damping force（Fs=240 kN）

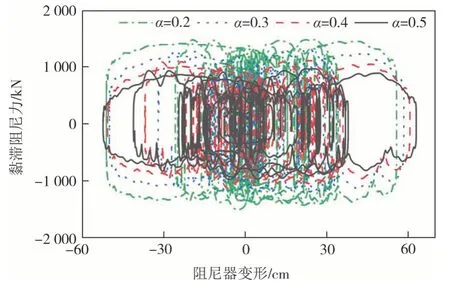
图22 黏滞阻尼力滞回曲线（C=2 000 kN·s·m-1）Fig.22 Hysteretic curves of viscous damping force（C=2 000 kN·s·m-1）

摩擦力滞回曲线与恢复力模型吻合很好，摩擦力增大，滞回曲线更加饱满，耗能增加.对于电涡流阻尼力滞回曲线，电涡流阻尼系数增大，阻尼力增大，滞回曲线越饱满，同时阻尼器变形减小，说明其对梁端纵向位移控制效果增加.

对比黏滞阻尼力和电涡流阻尼力滞回曲线，两者均在阻尼器小变形附近较为密集，阻尼器耗能较多.对于电涡流-摩擦组合型阻尼器，仅在少数阻尼器变形处达到较大阻尼力，阻尼力波动明显，而黏滞阻尼器在变形范围内均有较大的阻尼力产生，阻尼力较为稳定.

图23 为地震作用下全桥4 个阻尼器摩擦力耗能、电涡流阻尼力耗能及阻尼器总耗能随阻尼系数和摩擦力变化图.增大电涡流阻尼系数，可显著提高电涡流阻尼力耗能，从而增加阻尼器总耗能，但摩擦力耗能降低，这是由于电涡流阻尼系数增加导致梁端纵向位移减小，从而使摩擦力做功减少.随阻尼系数增加，电涡流阻尼耗能明显大于摩擦力耗能，电涡流-摩擦组合型阻尼器地震作用下主要以电涡流阻尼抑震为主.

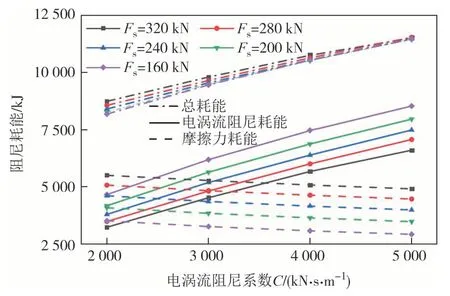
图23 电涡流-摩擦组合型阻尼器耗能Fig.23 Energy dissipation of eddy current-friction combined dampers

由于组合型阻尼器总耗能受摩擦力影响较小，所以选取Fs=160 kN 时组合型阻尼器与黏滞阻尼器耗能进行对比研究，如图24 所示.由于黏滞阻尼器阻尼力较大，导致黏滞阻尼器耗能明显大于组合型阻尼器，阻尼器耗能基本与阻尼系数呈线性增长关系.相较于阻尼系数，阻尼指数对阻尼器耗能影响较大，减小阻尼指数可以明显提升阻尼器耗能.

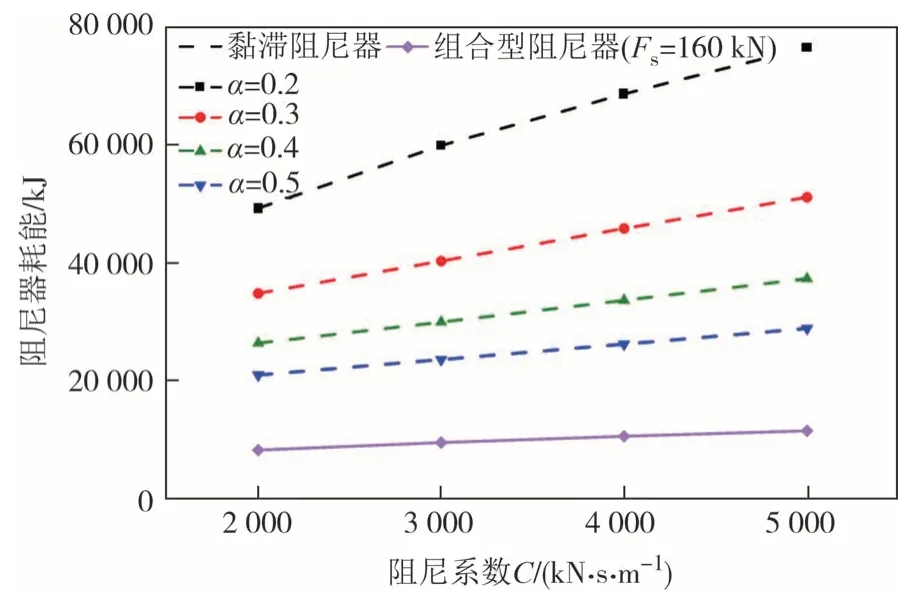
图24 组合型阻尼器与黏滞阻尼器耗能对比Fig.24 Energy dissipation comparison of eddy current-friction combined dampers and viscous damper

4.3 阻尼器优化设计

综合上述分析，地震作用下，对于大跨悬索桥增设阻尼器对桥塔底部内力响应影响不大，阻尼器主要用于控制梁端纵向位移.从阻尼器类型角度，考虑电涡流-摩擦组合型阻尼器与黏滞阻尼器两者本构模型差异，同一阻尼系数电涡流-摩擦组合型阻尼器阻尼力小于黏滞阻尼力，但是电涡流-摩擦组合型阻尼器对梁端纵向位移提供更为显著.另外电涡流-摩擦组合型阻尼器参数受环境温度影响小，减震效果更为可靠，工程适用性更好，所以选取电涡流-摩擦组合型阻尼器用于燕矶长江大桥减震控制.

综合考虑地震作用下电涡流-摩擦组合型阻尼器电涡流阻尼力和摩擦力占比关系、对梁端纵向位移的控制效果以及对塔底弯矩的影响，并比较电涡流阻尼力和摩擦力滞回曲线的饱满度及阻尼器耗能，最终选取阻尼器参数为阻尼系数C=4 000 kN·s/m，摩擦力Fs=240 kN，根据该阻尼器参数计算得到“纵向+竖向”地震作用下梁端纵向位移时程曲线如图25所示.

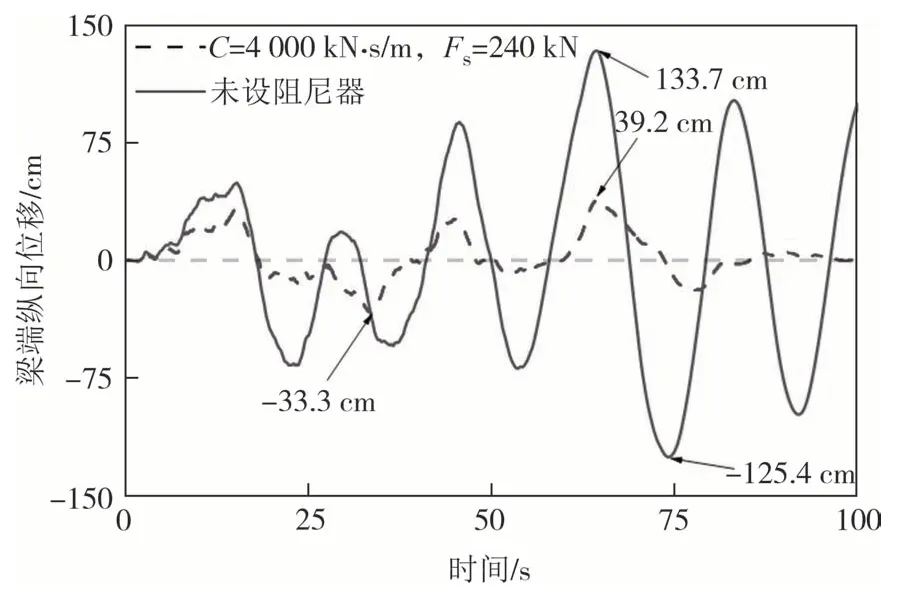
图25 梁端纵向位移时程曲线（C=4 000 kN·s·m-1，Fs=240 kN）Fig.25 Longitudinal displacement time-history curves at girder end（C=4 000 kN·s·m-1，Fs=240 kN）

5 结论

本文以燕矶长江大桥为工程背景，建立主桥有限元模型，采用非线性时程分析方法进行抗震性能验算，对比分析了电涡流-摩擦组合型阻尼器和黏滞阻尼器参数优化设计，并从耗能角度分析了地震作用下电涡流-摩擦组合型阻尼器减震特点，得到如下主要结论：

1）大跨悬索桥自振周期较长，低阶振型主要由加劲梁参与，燕矶长江大桥一阶自振周期21.45 s，为加劲梁一阶正对称侧弯振型.

2）E2 地震作用下，燕矶长江大桥桥塔各关键截面弯矩需求均小于截面抗弯能力，符合E2 抗震性能目标；但“纵向+竖向”地震作用下加劲梁梁端纵向位移峰值达到133.7 cm，需采取控制措施.

3）纵桥向设置组合型阻尼器和黏滞阻尼器均可有效降低梁端纵向位移，增加摩擦力、阻尼系数和降低阻尼指数，可提升对梁端纵向位移控制效果.但对于高塔、大跨悬索桥，地震作用下塔底弯矩主要与主缆引起的塔顶剪力和桥塔自身质量、高度有关，设置阻尼器后对塔底弯矩影响较小.

4）增大阻尼系数，可提升组合型阻尼器总耗能；随阻尼系数增加，电涡流-摩擦组合型阻尼器中电涡流阻尼耗能增加，摩擦力耗能减少.阻尼系数较大时，组合型阻尼器地震作用下以电涡流阻尼抑震为主.

值得指出的是，本文主要关注四主缆悬索桥的阻尼器优化设计，然而从抗震性能和工程设计角度而言，四主缆大跨悬索桥与常规双主缆悬索桥理论上存在较明显的差别，显然需要进一步深入研究以满足这种桥型的抗震设计需求.