基于轨道静检的动检里程偏差修正算法研究
刘星辰,李阳腾龙,黄 亿,魏勇超,岑敏仪
(1.西南交通大学 地球科学与环境工程学院,四川 成都 610031;2.成都理工大学 地球科学学院,四川 成都 610059;3.西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031;4.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043;5.广深铁路股份有限公司 广州南高铁工务段,广东 广州 511495;6.广州地铁集团有限公司,广东 广州 510000)
轨道几何状态动态检测里程测量采用光电编码器进行脉冲测量,经过处理计算得到里程[1]。由于光电编码器的动态误差[2]、车轮空转打滑[3]、检测人员置入检测系统的误差[4]等因素的影响,动态检测数据不可避免地产生里程偏差,导致波形错位,直接使用存在里程偏差的数据将会影响轨道质量状态的评估精度以及线路状态恶化趋势分析的可靠性,无法确保线路现场养护维修效果。
为解决轨道动态检测数据的里程偏差,国内外学者从外部和内部基准修正两个方向进行相关研究。外部基准修正方法通过加装硬件(GPS[5]、DGPS[6]、RFID[4]、相机[7])获取当前动检车所在线路里程的位置进行修正,或者通过从检测数据中识别线路特征点(钢轨焊缝[8]、关键设备[9]),再通过已知的特征点线路里程进行偏差校正,实现里程校正的目的。内部基准修正方法通过两次动检数据中同类参数间的相似关系,利用数学工具(互相关分析[10-11],互相关分析+自回归移动平均模型+蒙特卡洛模拟+卡尔曼滤波[12],五点迭代法[13],相关系数法[14],灰色关联法[15],动态时间规整[9])确定两次动检数据之间的里程偏差,以此统一两次动检数据的里程基准。此外,魏晖等[16]基于轨向或高低数据采取动态时间规整算法实现动检数据与静检数据的匹配校准。
现有外部和内部基准修正方法均能按照用户需求有效地对动检数据里程偏差进行修正,但仍然存在不足。加装硬件的外部基准修正方法,需要定期对新增设备进行维护,成本较高,且修正精度受环境的影响较大。从检测数据中识别线路特征点依赖于识别的精度,且仅通过线路特征点进行线路里程修正无法保证全线的修正精度,距离特征点越远的检测点修正精度越低。动检数据间的内部基准里程修正后与线路里程仍存在误差,误差大小取决于所采用的基准动检数据里程与线路里程的实际误差。由于轨道检测轨向、高低等各通道参数在轨道几何状态变化中的变化速率不同,基于轨向或高低等某一通道数据为依据进行里程误差修正,不可避免会出现里程修正值不符的情况,且使用不同通道的数据,里程修正结果也不同。
动检数据与静检数据之间既存在差异性[17],又具有一定的相关性[18],只有消除二者之间的里程偏差才能对其差异性及相关性进行分析研究。而且静检数据容易获得线路里程,只要在轨道动态检测前或后进行静态检测,就能充分利用动静检数据波形的相似性,实现动检数据的里程误差修正,并使修正后的动检数据更接近于线路里程。从而实现动静态检测数据的联合分析研究,更好地指导轨道养护维修。
1 里程偏差修正算法
动检数据里程和线路里程最大的误差可在百米以上[9]。较大的里程偏差修正需利用曲线段的平曲线主点处超高特性,采用道格拉斯-普克(Douglas-Peucker,D-P)拟合迭代算法提取平曲线主点里程[19]。将提取的动静检平曲线主点对应起来,然后在静检超高数据中,以静检平曲线主点为中心,区段长度L作为待匹配段。在动检超高数据中,以对应的动检平曲线主点为中心,L+20 m范围作为搜索区域搜索最匹配段,如图1所示,图1中,ZD为提取的平曲线主点。
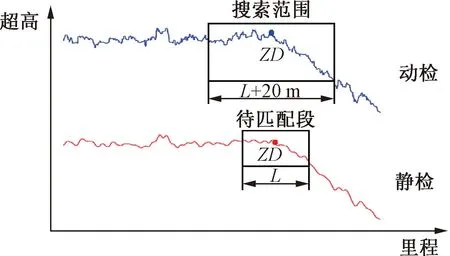
图1 曲线主点超高波形匹配示意
以波形较差的标准差作为相似性度量准则,在动检搜索范围内逐检测间隔计算与静检待匹配段超高波形相似性,然后求其最小值即为最佳匹配段。
( 1 )
式中:ρ为动静检波形较差的标准差;xi、yi分别为动检、静检第i个检测数据;n为区段中的测点个数。
最佳匹配段的中点为新主点,将N个动检新主点的里程与对应的静检曲线主点里程对齐,计算相邻两新主点的里程偏差量差值ei,即
ei=(Xi+1-Yi+1)-(Xi-Yi)
( 2 )
式中:Xi和Yi分别为动检和静检的第i个主点,i=1,2,…,N-1。
将ei分配给两主点间的检测数据,两主点间的所有测点里程增加ei/n,n为两主点间测点个数,完成平曲线主点处里程偏差修正,简称第一次里程修正。
N个里程校正后的主点将动检与静检数据分为N+1段,分别对每一段静检轨向高低偏差数据以区段长度L进行分段,与动检轨向高低偏差数据进行区段匹配,综合考虑轨向高低四个通道的均值化标准差作为相似度判断依据。
( 3 )
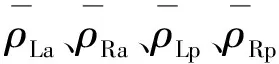
通过式( 1 )和式( 3 )求出相似度最高的区段,区段中点为新的里程校正点。将动检校正点的里程与对应的静检里程对齐,然后将相邻两校正点的里程偏差量差值平均分配给两校正点间的检测数据,如此循环迭代进行,直到所有校正点的距离小于L,结束循环完成里程修正,简称第二次里程修正。
同一组动检数据使用不同的里程偏差修正方法,所呈现出的修正效果是不同的。因此需要对修正算法的效果进行科学、合理的评价。已有研究表明,相同里程范围没有轨道维修作业时,轨道动检数据波形具有相似性,仅存在幅值大小的差异[20],高平顺的高速铁路轨道,动静态波形差异较小[21]。因此,可以通过轨向高低不平顺波形的相似性对修正效果进行评价。由于动静检轨向高低不平顺值较差的真实值未知,其真误差无法准确得到,因此使用较差的不确定度μA对修正算法的结果进行评定更为科学,其计算式为
( 4 )
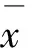
不确定度表征被测量的真值所处量值范围的评定[22],一方面便于评定其可靠性,另一方面也增强了测量结果之间的可比性。不确定度越小表示测量结果越接近真值相关系数r代表动静检波形的整体相关程度,其计算式为
( 5 )
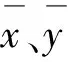
综合考虑校正后轨向高低不平顺值较差均值,99.9%置信概率的不确定度和相关系数对里程偏差修正精度进行评价。均值和不确定度越小,相关系数越大则校正效果越好。
2 实验分析
2.1 仿真数据实验
受各种偏差的影响,无法获取实测数据真实里程误差,因此需要通过仿真数据验证算法的精度。由于区段匹配的里程偏差修正效果会受匹配区段长度的影响[14]。为避免错误匹配、提高修正精度,需要进行匹配区段长度的实验。使用主点迭代里程偏差修正(principal point iteration correction,PPIC)算法分别对不同匹配长度进行模拟数据里程偏差修正,通过和真实里程误差对比,得出适用于待校正数据的匹配区段长度。所使用的静检数据为某高速铁路K2298+700—K2303+000、K2305+100—K2308+100、K2310+100—K2313+100三段轨道静态实测数据,里程间隔0.125 m,检测数据包含里程、超高、轨向和高低等不平顺值数据。基于静检数据进行动检数据模拟,将数据分为匀加速段(K2298+700—K2303+000) 车速从150 km/h加速至250 km/h;变加速段(K2305+100—K2308+100)车速从250 km/h加速至350 km/h;匀速段(K2310+100—K2313+100)车速350 km/h。变加速段检测点个数为n,相邻两点的速度变化量V=100/(n-1)km/h,根据变加速段的长度估算V约为0.004 km/h,在其基础上添加服从μ=0,σ=±0.004 km/h的正态分布的随机误差,以此来模拟每个点的加速度不同的变加速过程。当光电编码器的转动速度为v时,由于光电编码器存在数据处理时间t,使得每次输出数据时产生延时误差[2]Δt,即
Δt=vt
( 6 )
假设光电编码器数据处理时间t为10-6s,根据式( 6 )计算每个点的延时误差,各点里程加上延时误差得到模拟动检里程。对超高、轨向和高低等偏差数据按照动检间隔0.25 m进行重采样得到模拟动检数据。
分别选择10、30、50、70、100 m匹配长度进行实验,通过PPIC算法计算得到里程误差与误差真值之差的均值,均值越小说明其精度越高。区段长度与校正精度的关系如图2所示。从图2中可看出,三段数据均为50 m匹配区段长度校正效果最佳,因此采取50 m匹配区段长度对三组模拟数据进行里程偏差修正。
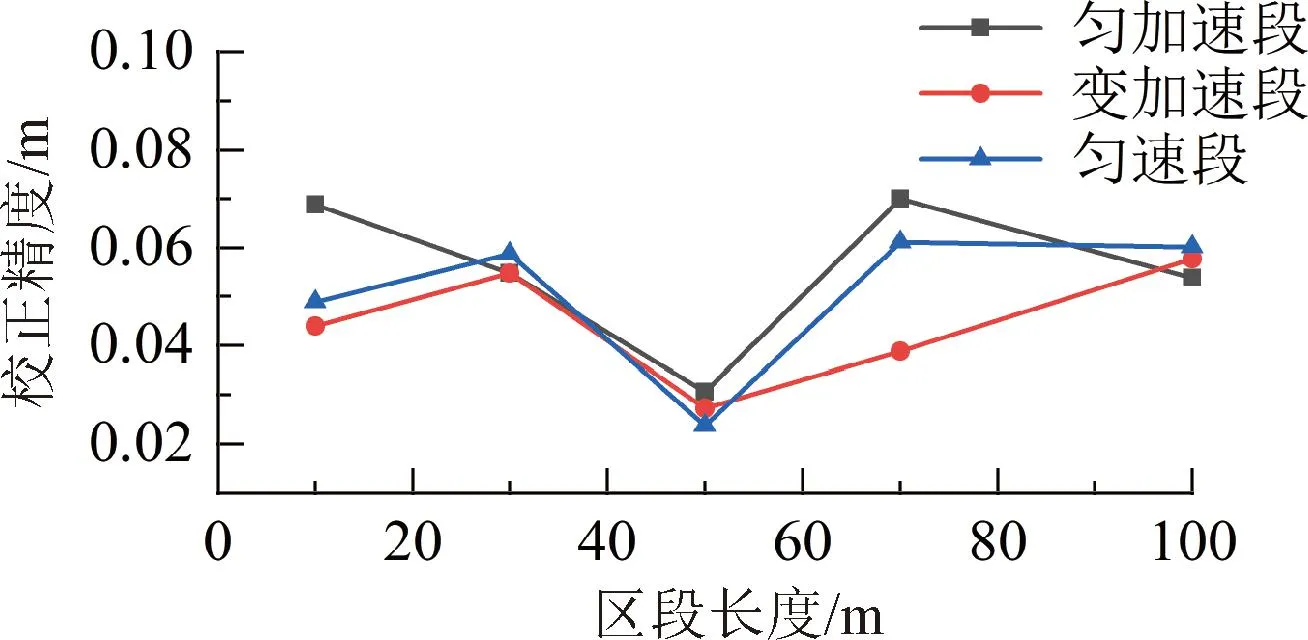
图2 不同匹配长度校正效果
传统里程偏差修正方法中常用的是区段相似波形匹配(segment similar waveform matching,SSWM)[23]算法,该算法比较稳定,可有效修正里程偏差且不会出现数据丢失现象,算法通过计算寻找曲线相关系数最大值进行匹配实现。为验证PPIC算法的有效性,使用PPIC算法进行模拟数据实验,并以传统里程偏差修正算法中的SSWM算法为代表,比较PPIC算法与传统里程偏差修正算法的修正精度问题。静检基准数据与模拟动检数据为前文所述数据。分别对两种算法进行修正效果评价,见表1。
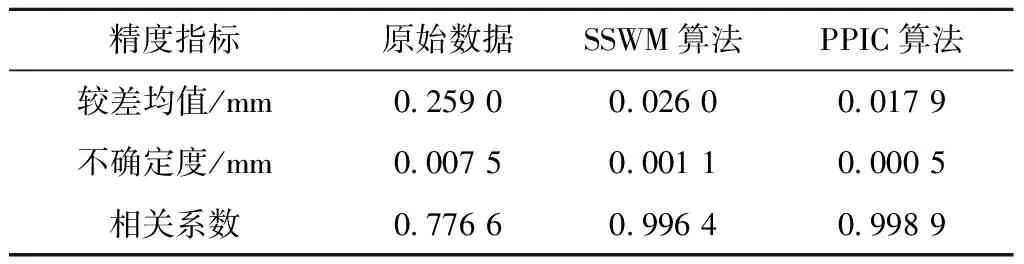
表1 模拟数据修正效果评价
由表1可知,两种算法修正后轨向高低较差均值、不确定度接近0,相关系数接近1,均接近完全修正值。PPIC算法较差均值、不确定度更小,相关系数更大,修正效果更优,修正后里程偏差最大值小于0.125 m,修正精度可控制在一个静检间隔内。两种算法得到的里程误差与误差真值之差的均值、标准差、最大值如表2所示。
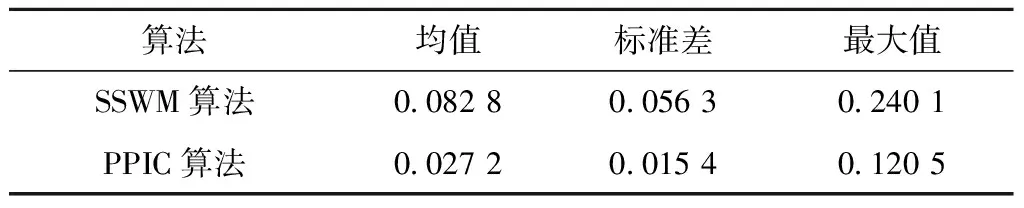
表2 算法里程误差与误差真值对比 m
由表2可知,PPIC算法的均值、标准差相较于SSWM算法减少约70%、最大值减少约50%。
2.2 实测数据检验
为验证算法对动静检里程偏差修正的实用性,采用三组速度为350 km/h高速铁路轨道动静检实测数据实践检验。三组数据轨道静检里程分别为K2298+700—K2303+000、K2302+600—K2305+800、K2305+000—K2308+100,分别为1、2、4月检测所得,数据采样间隔0.125 m,对应的轨道动检数据分别为与之检测时间最邻近的数据,为动检车测量所得,数据采样间隔0.25 m。
同样采取不同匹配长度对上述三组高铁实测数据进行PPIC算法里程偏差修正实验,结果见表3。从表3中可以看出,50 m匹配长度的较差均值最小,相关系数最大,30、50、70、100 m的不确定度相等,均大于10 m 的不确定度。因此,采取50 m匹配区段长对三组实测动检数据进行里程偏差修正。
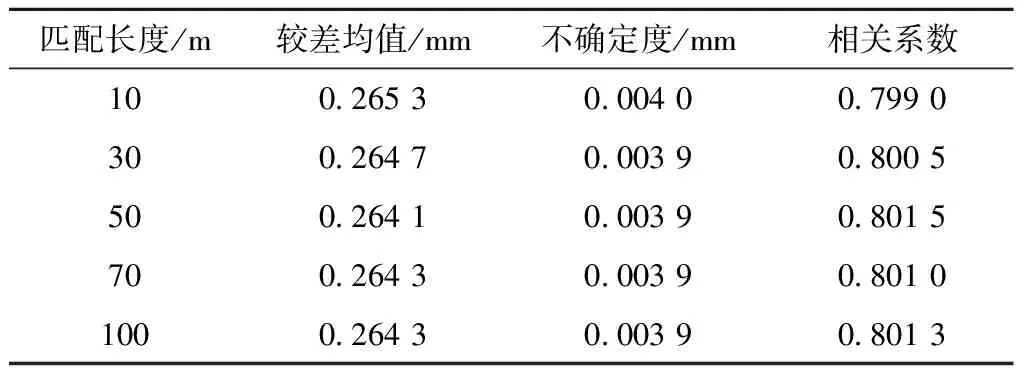
表3 实测数据不同匹配长度修正效果评价
分别使用PPIC算法和SSWM算法进行修正,效果评价见表4。
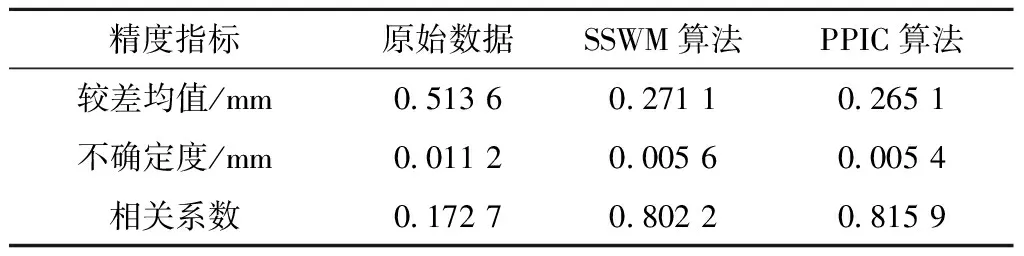
表4 实测动静检数据修正效果评价
两种算法修正后轨向高低较差均值与不确定度减少了近50%,相关系数提升近4.5倍。PPIC算法较差均值、不确定度更小,相关系数更大,修正效果更优。
由于动静检数据之间本身存在着幅值上的差距,因此校正后距离较差均值、不确定度等于0,相关系数等于1还存在一定的差距,而相同里程范围没有轨道维修作业时,同为动检数据幅值的差异相对较小,对比四次动检数据的轨向高低不平顺值较差均值、不确定度和相关系数列于表5。从表5中可看出,修正后四次动检数据之间轨向高低较差均值、不确定度接近0,相关系数接近1。PPIC算法各项指标均优于SSWM算法,修正效果更优。
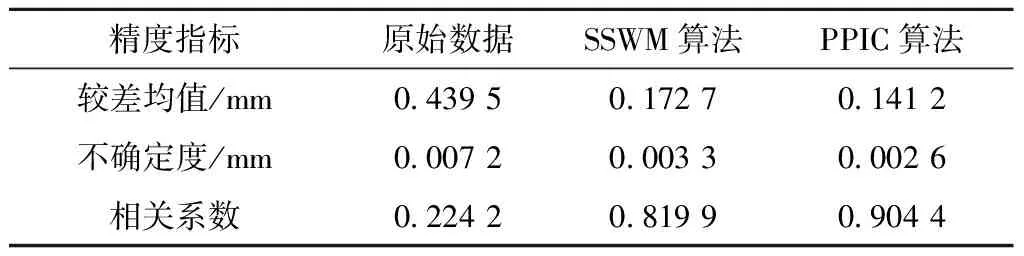
表5 四次动检数据修正效果对比
图3为实测动检原始数据轨向和高低不平顺值随里程变化的波形与静检基准数据的对比。图4为静检数据对应的四期动检原始数据轨向和高低不平顺值随里程变化的波形对比。由图3、图4可以看出,动静检以及四期动检轨向高低波形吻合度低,动静检数据间均存在约170 m的里程偏差,如图3(a)、图3(b)中框格所示,蓝色框格内的动检数据与红色框格内的静检数据相对应。图4框格中的数据是相对应的,可明显看出各期数据存在不同大小的里程偏差。
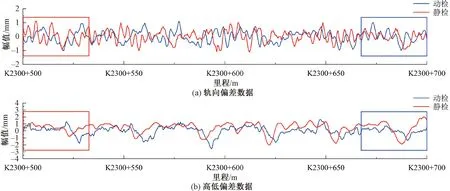
图3 动静检原始数据波形对比
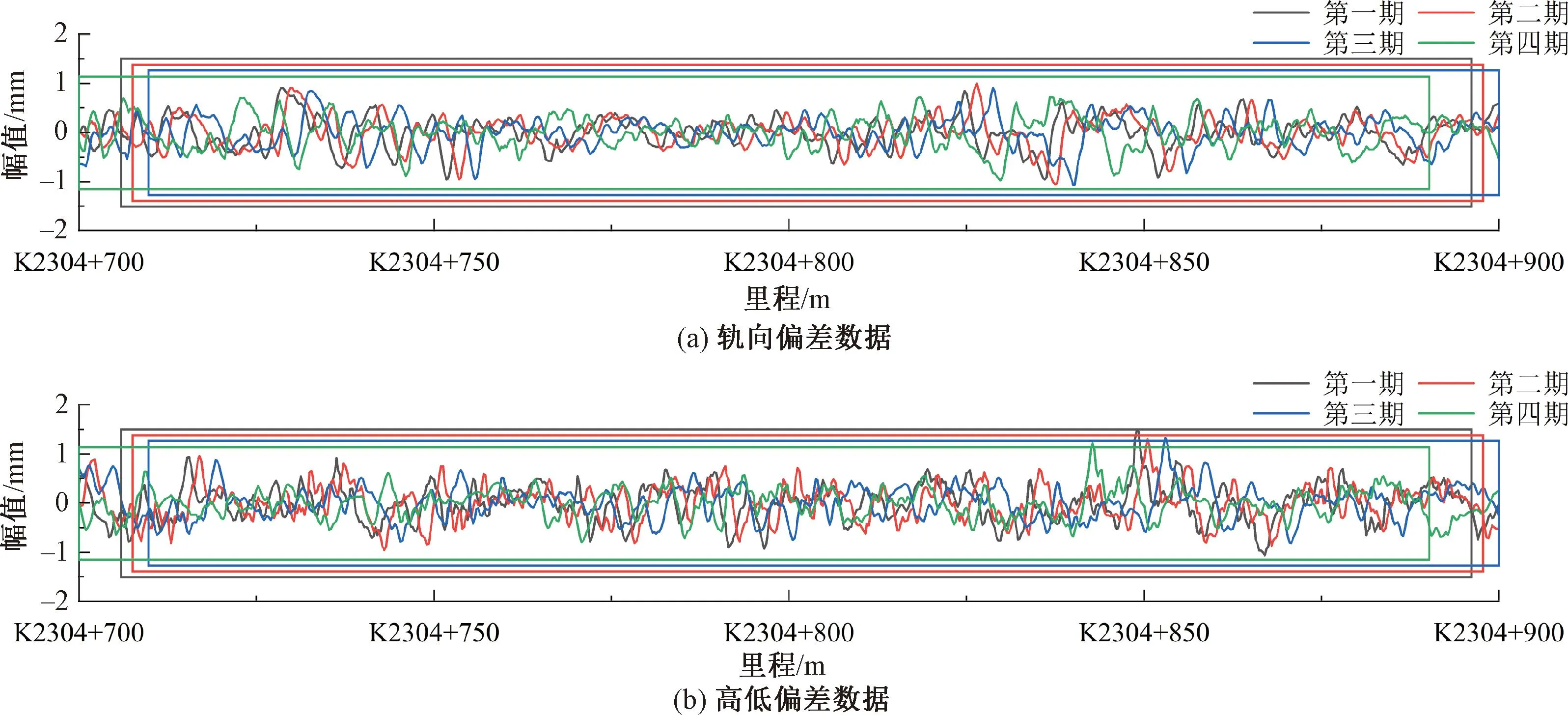
图4 四期动检原始数据波形对比
图5和图6分别为PPIC算法里程偏差第一次和第二次修正后实测动检轨向高低不平顺值随里程变化的波形与静检基准数据的对比。图7和图8分别为PPIC算法里程偏差第一次和第二次修正后四期动检数据轨向高低不平顺值随里程变化的波形对比。从图5和图7中可以看出,经过里程偏差第一次修正后动静检波形和四次动检波形的吻合度大幅提升,但仍存在明显的里程残差。从图6和图8中可以看出,经过第二次修正后动静检波形和四次动检波形达到较高的吻合度,四次动检波形近乎重合。因此,PPIC算法可以有效的对动静检里程偏差进行修正。
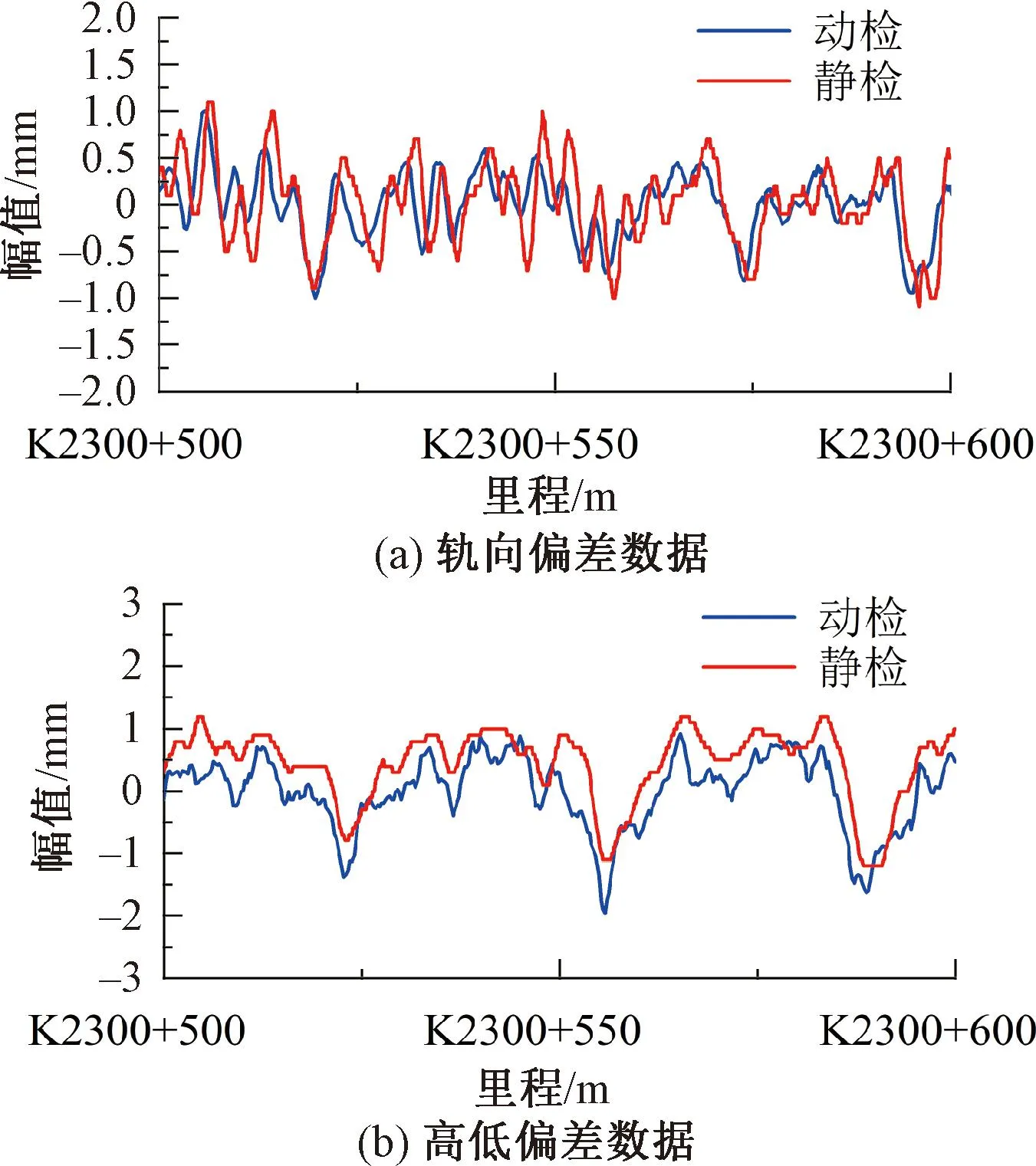
图5 里程偏差第一次修正后动静检数据波形对比
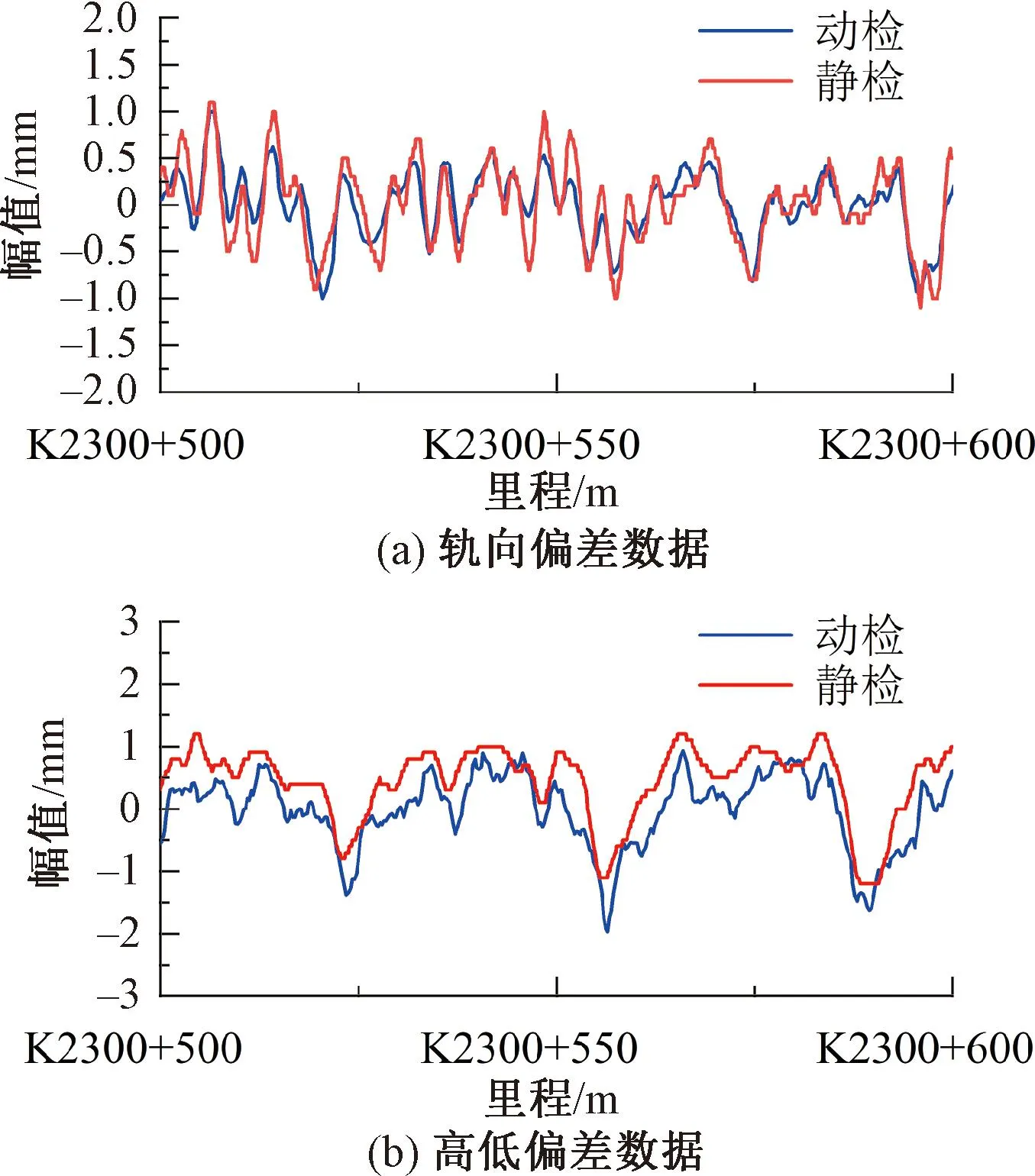
图6 里程偏差第二次修正后动静检数据波形对比
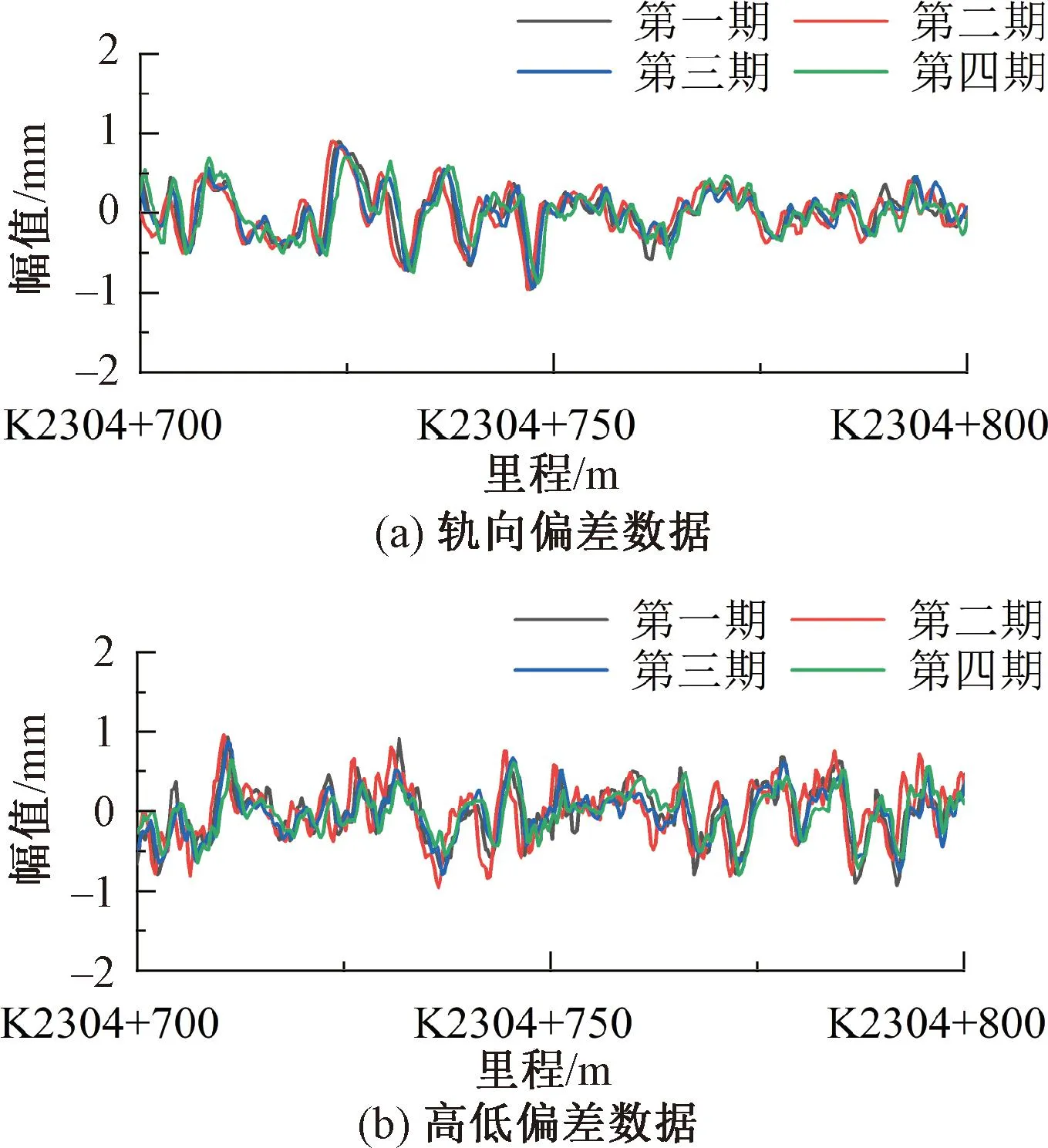
图7 里程偏差第一次修正后四期动检数据波形对比
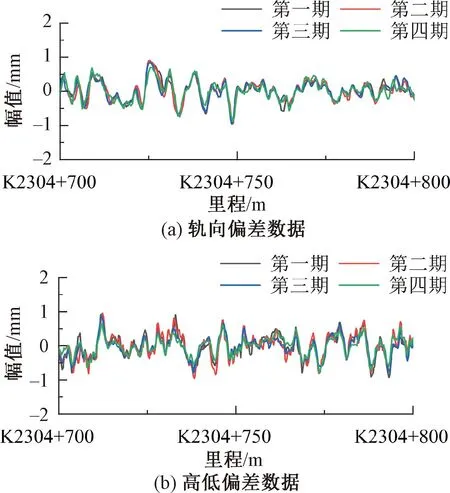
图8 里程偏差第二次修正后四期动检数据波形对比
3 结论
面对现存相对里程偏差修正算法的不足,分别采用PPIC算法和轨向高低不平顺值较差均值,99.9%置信概率不确定度和相关系数的综合评价标准,解决错误匹配、数据丢失、匹配效率低的问题。经轨道仿真数据实验和动静检高速铁路实测工程数据检验,并将传统里程偏差修正算法中的SSWM算法与PPIC算法进行比较,证实所提标准和算法的有效性和统计数据的精确性,得到以下结论:
1) PPIC算法解决了传统SSWM相对里程偏差修正方法中时间复杂度高、存在错误匹配等问题。
2) PPIC算法能有效的对动检数据里程偏差进行修正,修正后动静检波形吻合度大幅提升,波形较差均值与不确定度减少了近50%,相关系数提升近4.5倍,且修正效果优于传统里程偏差修正算法中的SSWM算法。
3)PPIC算法里程偏差修正精度可控制在一个静检检测间隔(0.125 m)内。
需要指出的是,50 m匹配区段长虽经仿真和工程实测数据检验,但动静检数据量还不充足,尚需在后续的工程应用中进一步验证。

