融合轨面短波不平顺的全波段高低不平顺谱表征及影响分析

杨 飞，魏子龙，孙宪夫，郭战伟，杨国涛，熊凯舟

(1.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；2.中国国家铁路集团有限公司 工电部，北京 100844；3.中国国家铁路集团有限公司 科技和信息化部，北京 100844；4.中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081)

截至2023年底,我国高速铁路(以下简称“高铁”)运营里程已达4.5万km,其中速度300～350 km/h的高铁里程已超过1.5万 km。在高铁系统中,轨道作为支撑列车运行的关键载体,其几何不平顺会加剧车辆与轨道间的动力相互作用,缩短列车与轨道结构的维修周期和使用寿命,甚至影响高速行车的安全性和平稳性。因而,科学、准确地评价轨道平顺状态,是保持高铁轨道服役性能的必然要求。

在各类轨道平顺性评价方法中,轨道不平顺谱作为描述轨道不平顺的大小随空间频率变化的指标[1],是表征轨道不平顺幅频特性的有效工具。一方面,轨道不平顺谱作为输入激励,在分析和评估车辆、线桥隧结构的动力性能中起到重要作用;另一方面,轨道不平顺谱还能从宏观角度反映轨道不平顺状态,是指导养护维修的重要参考。此外,短波不平顺谱还被广泛应用于轮轨振动、噪声分析[2]。

轨道不平顺谱的统计和分析一直是国内外研究的热点。受限于测试手段,轨道不平顺谱大多由轨道检查车等大型检测设备测试数据拟合得到,适用于波长在2 m以上的中长波不平顺[3-4]。

对于中长波轨道不平顺谱,自20世纪60年代起,英、法、日、美、德就相继发布了适用于不同线路和速度等级的轨道不平顺谱[5-6]。我国从20世纪80年代至今,先后发布了原长沙铁道学院谱、中国三大干线谱、秦沈客运专线谱、武广高铁谱、高铁无砟轨道不平顺谱和高铁有砟轨道不平顺谱等一系列具有代表性的轨道谱[3-4,6-10],其中最新提出的轨道谱也要追溯至2016年[4]。此外,国内学者[11-12]分别针对部分普速铁路、高铁或城市轨道交通线路提出相应的轨道不平顺谱和轨道状态评价方法。近年来,随着高铁运营期的增长,既有高铁轨道几何状态逐渐发生变化,尚缺少能够准确描述当下轨道几何状态的轨道不平顺谱;与此同时,在新开通的大量高铁线路中,CRTSⅢ型板式无砟轨道得到了广泛应用,以往提出的轨道不平顺谱对该型轨道结构的分析较少。面对未来高铁更高运营速度的要求,亟需提出能够表征当前高铁轨道几何状态的轨道谱。此外,高速综合检测列车难以准确测量波长在2 m 以下的短波不平顺,但其所搭载的车辆(轴箱、转向架构架、车体)全断面加速度检测系统和连续式轮轨力检测系统能够获取更宽频段的车辆动力学响应,相关评价指标也在逐渐纳入管理标准,亟需探索与之相对应的全波段轨道不平顺,而目前尚未有研究提出能够同时考虑中长波和短波成分的全波段轨道不平顺谱。尽管可以借助既有中长波轨道谱向短波长方向外推全波段谱,但其结果的准确性有待考证[13]。

随着列车速度的提高,轨面短波不平顺对车轮系统的激扰愈加突出。需要指出,当采用短波不平顺谱进行轮轨系统随机振动仿真时,往往需要考虑车轮与钢轨表面粗糙度共同作用。一种呈现形式是轮轨分离谱,即分别测量车轮和钢轨表面粗糙度后再进行叠加[14];另一种是考虑车轮和钢轨表面粗糙度谱相干性的轮轨联合粗糙度谱,其中Sato[15]于1977年提出适用于波长在3 m以下的轮轨表面粗糙度谱,被广泛应用在轮轨高频振动和噪声分析中[16-17]。徐志胜[14]在Sato谱的基础上结合秦沈客运专线噪声测试数据,采用黄金分割法反演出合适的轨面粗糙度系数。此外,也有部分研究聚焦于轨面粗糙度分析,而不考虑车轮表面粗糙度的影响。王澜等[18]以铺设50 kg/m钢轨的石太铁路为对象,提出有效波长范围为0.01～1 m的轨面粗糙度谱,其与Sato谱均采用幂函数形式。刘秀波等[19]基于对数坐标下的八次多项式曲线拟合广深线和京山线的钢轨焊接接头短波不平顺谱。马蒙等[20]采用分段幂函数拟合出波长范围为0.01～1 m的北京地铁轨面短波不平顺谱,并对不平顺状态进行分级。此外,也有学者[21-22]基于轨面粗糙度的1/3倍频程波长谱(轨面粗糙度级)对部分高铁和城市轨道交通线路的轨面短波不平顺状态水平进行分析。然而,既有研究鲜有对我国高铁短波不平顺谱进行深入分析,有必要开展我国高铁短波不平顺谱的制定工作。

本文首先基于多条无砟轨道高铁的轨面粗糙度测试数据,采用分段幂函数拟合轨面短波不平顺谱的表达公式。然后结合30余条无砟轨道高铁的动态轨道不平顺检测数据,采用高阶多项式拟合全波段高低不平顺谱的表达公式。最后以某高铁实测的车辆动力学响应数据为例,分析短波和中长波高低不平顺对车辆动力学响应的影响。研究成果将为轮轨振动仿真分析、车辆和轨道结构设计以及轨道状态评估提供参考和借鉴。

1 高铁钢轨轨面短波不平顺谱

1.1 测试方法与数据样本

采用钢轨波磨测试小车对京沪高铁、京津城际、京广高铁(京石武段)、徐兰高铁(郑西、宝兰段)、合福高铁等多条无砟轨道高铁线路开展测量试验,按照1 mm的采样间隔记录钢轨表面短波不平顺状态。测试区段涵盖区间与站区正线线路,平面线形包括直线、大半径曲线与小半径曲线,测试数据总长度达到58.415 km。轨面状态包含有波磨工况和无波磨工况,波磨区段包括打磨作业前后的测试数据。

1.2 轨面短波不平顺功率谱特征分析

采用1/3倍频程波长谱给出轨面短波不平顺粗糙度级,见图1。由于部分测试区段存在钢轨波磨,使得粗糙度级在1/3倍频程中心波长63 mm处较为突出。与BS EN ISO 3095—2013[23]规定的粗糙度级限值相比,实测数据在中心波长大于4 mm时普遍超限;与BS EN ISO 3095—2005[24]规定的粗糙度级限值相比,实测数据在中心波长介于5～31.5 mm和大于315 mm时超限[22]。

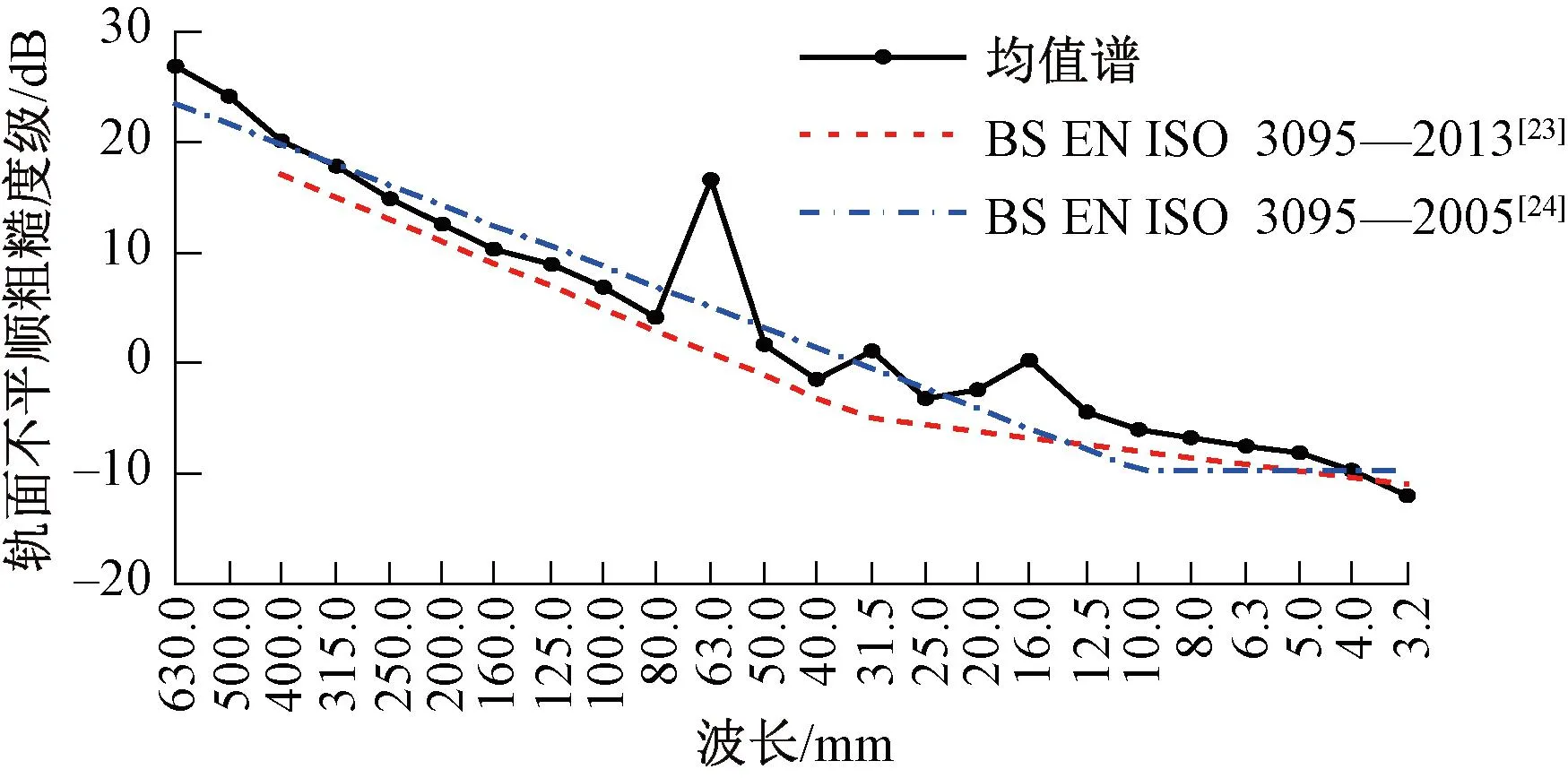
图1 短波不平顺粗糙度级与标准限值对比

为定量描述高铁钢轨磨耗严重程度,采用Welch提出的修正周期图法计算轨面短波不平顺谱[11],每个计算单元长度为4.096 m,结果见图2。分别对每个波长条件下的各计算单元短波不平顺谱值进行排序,选取1%和99%分位数作为短波不平顺谱的下限谱和上限谱。由图2可见,均值谱的整体幅值介于上下线谱之间,与上限谱更为接近。

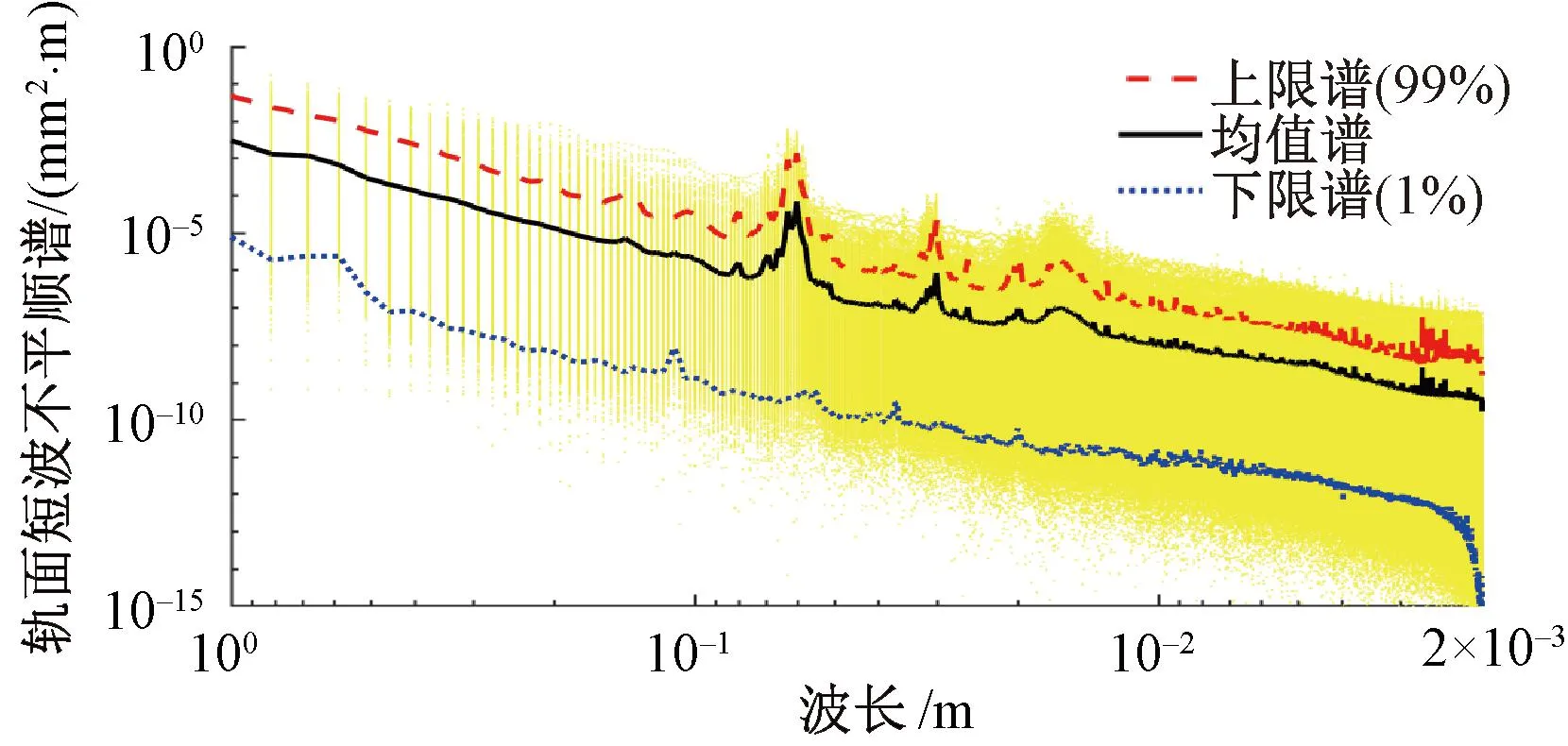
图2 高铁无砟轨道轨面短波不平顺谱

1.3 轨面短波不平顺谱拟合公式

考虑到波磨测试小车的测试精度以及轨面短波不平顺谱在仿真计算的应用场景,拟合波长范围取0.002～1 m。由于Sato谱和王澜谱采用的基于幂函数的拟合形式简单,便于使用,本文也采用幂函数对轨面短波不平顺谱进行拟合,即

S(f)=Af-k

( 1 )

式中:S(f)为不平顺功率谱,mm2·m;A、k为待拟合系数,A为功率谱的幅度,k为功率谱随空间频率的变化速率;f为空间频率,1/m。

对式( 1 )求对数后得到

q=-kp+lg(A)

( 2 )

式中:p=lg(f),1/m;q=lg[S(f)],mm2·m。

由式( 2 )可知,采用幂函数在双对数坐标系下对功率谱进行拟合时可以转换为对自变量p和因变量q的线性拟合。对0.002～1 m波段内双对数坐标系下的均值谱、上限谱和下限谱直接进行线性拟合时发现,在空间频率20 1/m附近均存在较为明显的分段特征。因此,将高铁轨面短波不平顺谱分两段幂函数进行拟合。

轨面短波不平顺均值谱拟合流程见图3。首先将均值谱转换至双对数坐标系下;然后对其进行等间隔重采样,以均衡各波长均值谱的拟合权重;再进行消峰处理提取出轨面短波不平顺的随机性成分;以空间频率20 1/m为首个分段点,分两段采用最小二乘法进行线性拟合,两条拟合直线的交点即为新的分段点;判断前后两次分段点空间频率是否小于给定阈值,否则根据新的分段点重新分段线性拟合,直至满足阈值条件完成拟合,系数拟合结果见表1。

表1 高铁轨面短波不平顺谱拟合公式系数

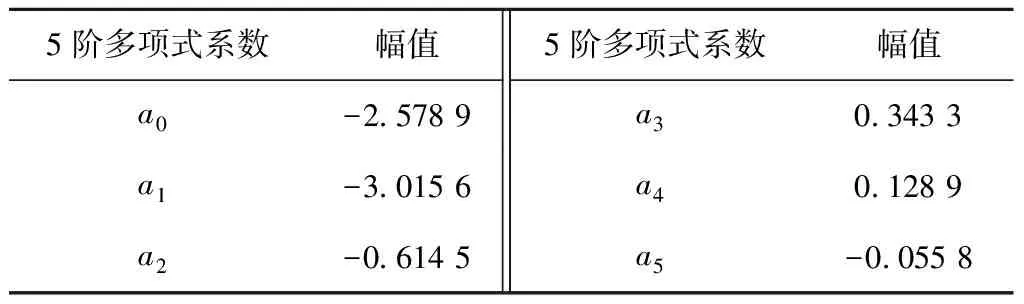
表2 高铁无砟轨道全波段高低不平顺谱拟合公式系数

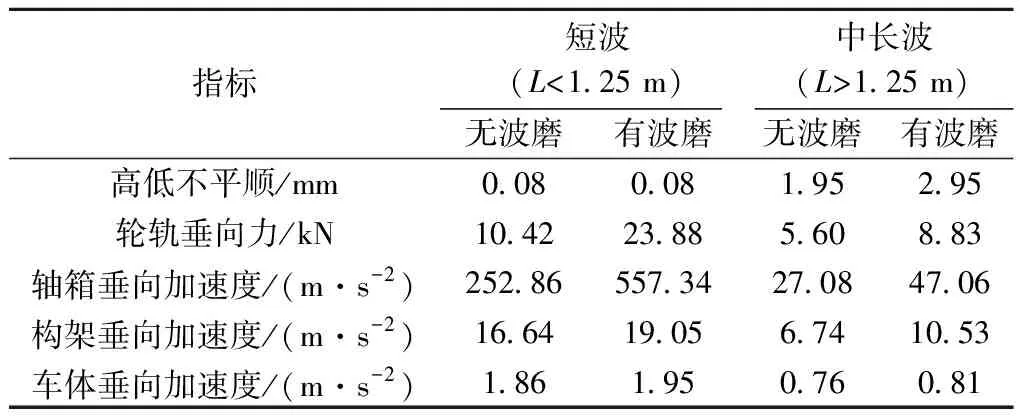
表3 实测高低不平顺和车辆动力学响应峰值(99%分位数)

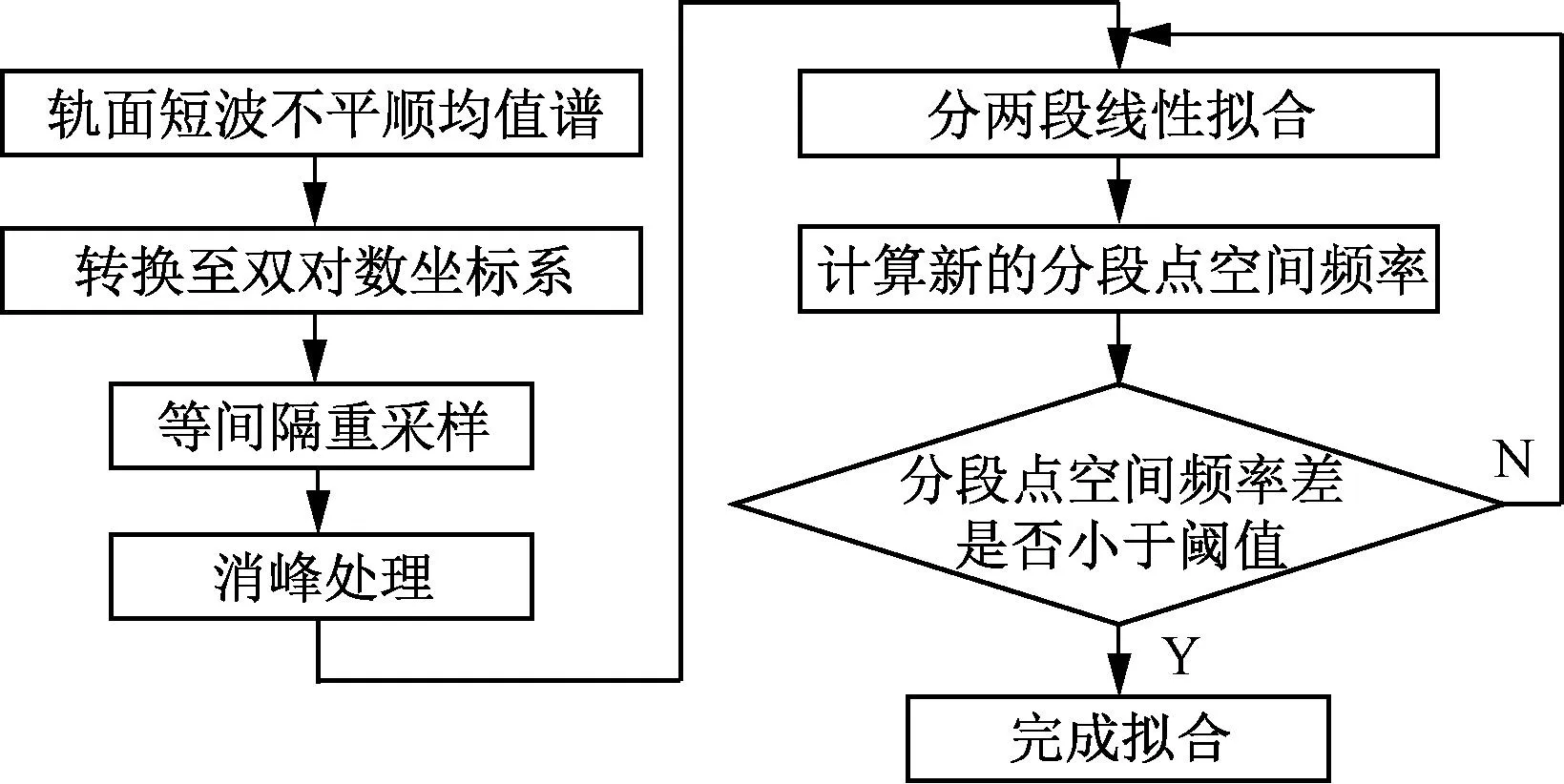
图3 轨面短波不平顺均值谱拟合流程

为了描述轨面短波不平顺谱的上下边界水平,引入系数b对上限谱和下限谱进行补充拟合,高铁轨面短波不平顺谱的最终拟合为

S(f)=10bAf-k

( 3 )

式中:b为待拟合系数。

系数b表示上限谱、下限谱相比于均值谱幅度的差距,b的引入能够保证这3种谱的拟合形式和变化趋势一致。通过变换系数b,当消峰处理后的上限谱(或下限谱)与分段幂函数在双对数坐标系下拟合误差整体最小时,得到上限谱(或下限谱)系数b的拟合结果见表 1,均值谱的系数b取0。

基于上述方法得到高铁轨面短波不平顺谱拟合结果,见图4。由图4可以看出,分段幂函数能很好地描述轨面短波不平顺随机性成分的变化趋势。在0.002～1 m波段范围内与常用短波不平顺谱对比发现:高铁轨面短波不平顺上限谱幅值整体小于Stao谱的上限谱;当波长小于0.025 m时,上限谱幅值大于Stao谱的下限谱;当波长小于0.045 m时,上限谱幅值大于王澜谱;其余波段上限谱幅值小于Stao谱的下限谱和王澜谱。均值谱幅值整体小于Stao谱;当波长小于0.006 m时,均值谱幅值大于王澜谱;其余波段均值谱幅值小于王澜谱。下限谱幅值均小于Stao谱和王澜谱。

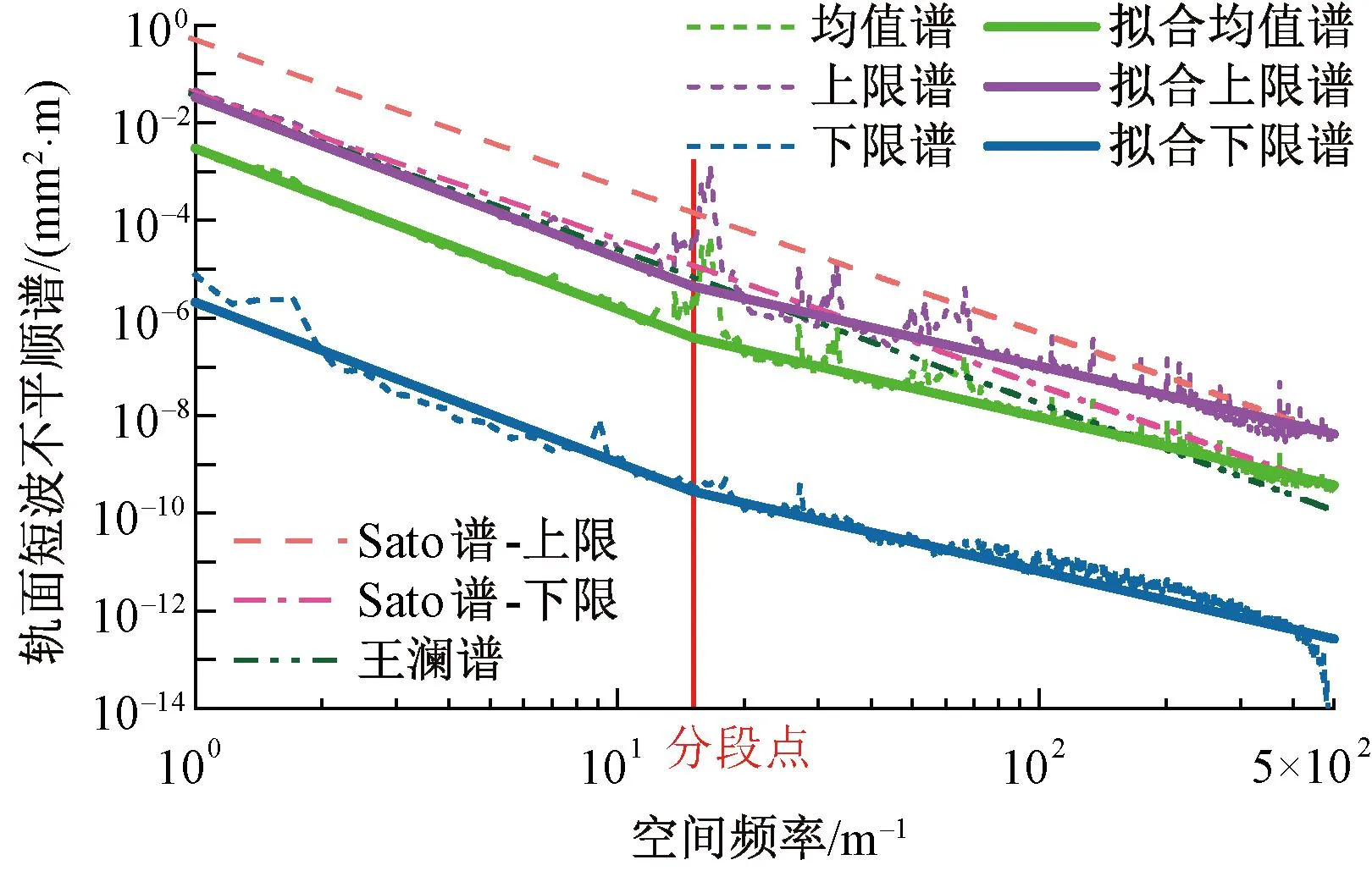
图4 高铁无砟轨道轨面短波不平顺拟合谱

2 高铁无砟轨道全波段高低不平顺谱

2.1 全波段高低不平顺谱特征分析

波磨测试小车在检测波长为1 m以下轨面短波不平顺时具备较高的可靠性,因此,全波段高低不平顺在1 m以下(短波)的成分采用波磨测试小车数据。高速综合检测列车对高低不平顺的可输出的波段为1.5～120 m,考虑到信号输出在截止波长附近被大幅衰减,将中长波不平顺分析波段设置为2～100 m,可以保证该波段内数据的可靠性。因此,全波段高低不平顺在2～100 m波段(中长波)内的成分采用高速综合检测列车采集的动态检测数据。

以30余条无砟轨道高铁线路的动态检测数据为基础,线路涵盖了CRTSⅠ型板式、CRTSⅡ型板式、CRTSⅢ型板式和双块式4种无砟轨道结构类型。采用Welch提出的修正周期图法计算这4种类型无砟轨道高低不平顺谱,即中长波高低不平顺谱。在计算前根据轨道不平顺变化率的限值3‰进行异常值剔除,计算单元长度取1 024 m。短波高低不平顺谱采用1.2节中计算的高铁短波不平顺谱。将中长波和短波高低不平顺谱与我国高铁无砟轨道标准谱[3]对比,见图5。由图5可知,对于中长波高低不平顺,CRTSⅢ型板式无砟轨道的随机不平顺状态最优,CRTSⅠ型板式无砟轨道的随机不平顺状态最差。CRTSⅡ型板板式与双块式无砟轨道的随机不平顺状态相当,两者在大多数波段介于CRTSⅠ型和CRTSⅢ型板式无砟轨道之间,且与高铁无砟轨道谱最为相近。

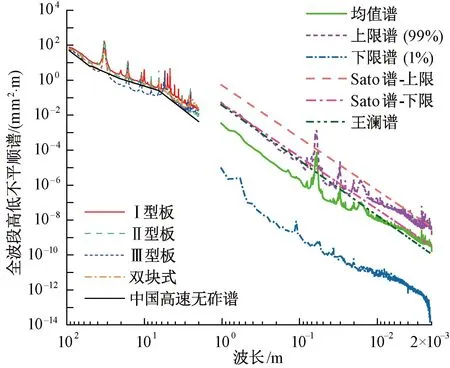
图5 高铁全波段高低不平顺谱

4种无砟轨道的中长波高低不平顺谱在波长2 m处的谱值介于0.99×10-2～2.38×10-2mm2·m之间,短波高低不平顺均值谱在波长1 m处的谱值为0.34×10-2mm2·m,略小于长波高低不平顺谱在2 m处谱值,符合高低不平顺谱波长从大到小、谱值逐级递减的客观规律。4种无砟轨道的中长波高低不平顺谱能够与短波高低不平顺谱在波长1～2 m之间平缓过渡。而Sato谱的上、下限谱和王澜谱在1 m处的谱值分别为53.69×10-2、4.50×10-2、3.88×10-2mm2·m,均大于长波高低不平顺谱在2 m处谱值最大值2.38×10-2mm2·m,长短波谱之间过渡会存在跳变,这也间接说明了具有代表性的轮轨联合粗糙度谱(Sato谱)以及50 kg/m钢轨普速铁路轨面粗糙度谱(王澜谱)并不能够有效反映我国高铁轨面短波不平顺状态的真实情况。

2.2 全波段高低不平顺谱拟合方法

目前,常见的轨道谱形式主要有幂函数和幂函数组合形成的多参数拟合公式。但对于全波段高低不平顺谱,其覆盖波长更宽,比既有的轨道谱多2个数量级的波长范围。此外,全波段高低不平顺谱的起伏变化较多,采用常规的拟合公式可能会产生诸多拟合参数,使用起来不够方便。为此本文采用高阶多项式对波长范围在0.002～100 m之间的全波段高低不平顺谱进行拟合。具体拟合方法如下:

首先将4种无砟轨道的中长波高低不平顺合并求得无砟轨道中长波高低不平顺均值谱,再将其转换至双对数坐标系后进行等间隔重采样,然后进行消峰处理并仅保留2～100 m的波长成分。将其与1.3节中提取出轨面短波不平顺的随机性成分合并后,采用n阶多项式拟合。具体采用Levenberg-Marquardt非线性最小二乘优化算法求解多项式特征项,即

q=a0+a1p+a2p2+···+anpn

( 4 )

式中:n为多项式阶数;a0,…,an为多项式特征项。

为寻找合适的多项式阶数,将阶数分别取2～9阶,计算得到全波段高低不平顺拟合谱相关系数见图6。由图6可知,相关系数随着阶数的增大逐渐提高,当阶数达到5阶时,相关系数变化趋于平缓,说明更高的阶数对拟合效果的提升作用不再显著。为简化拟合谱形式,将多项式阶数取为5阶,得到高铁无砟轨道全波段高低不平顺拟合谱见图7,拟合参数见表 2。由图7可知,采用5阶多项式拟合谱很好地反映了全波段高低不平顺谱随机性成分的变化趋势,并且使得中长波和短波成分在1～2 m的搭接波段实现了平缓过渡。

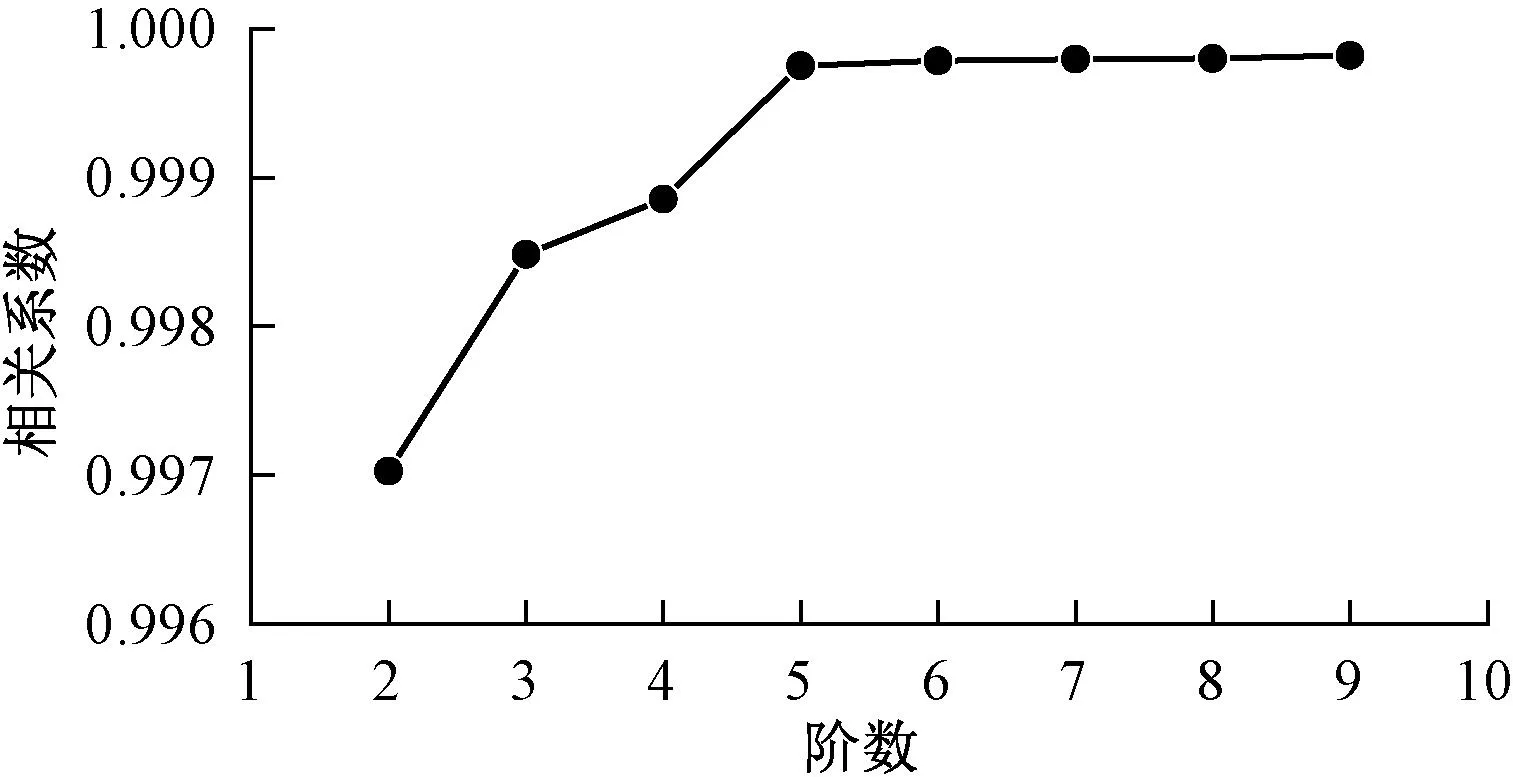
图6 各阶数多项式拟合谱的相关系数

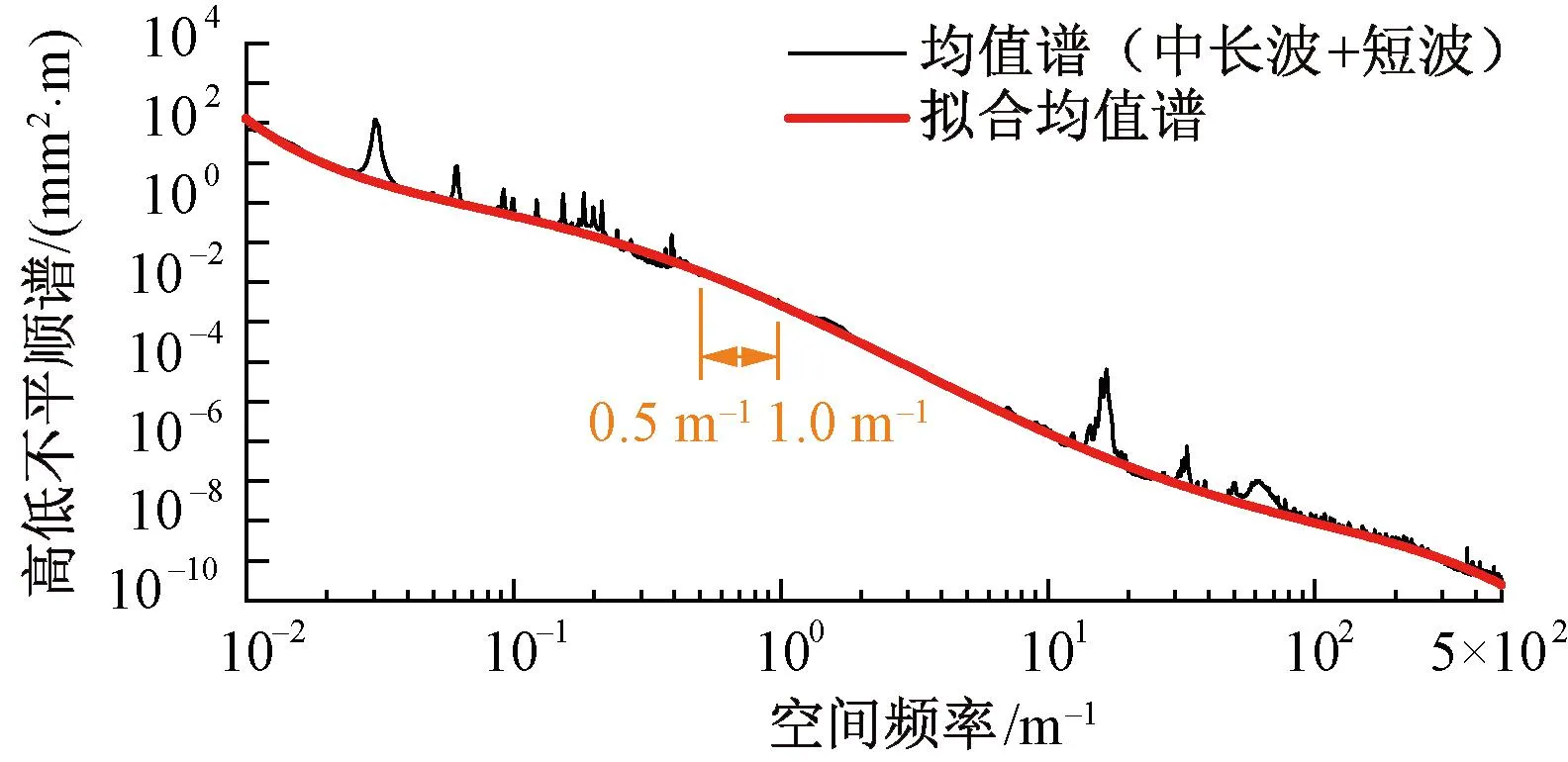
图7 高铁无砟轨道全波段高低不平顺谱

2.3 全波段高低不平顺谱反演效果

轨道不平顺谱的反演方法主要有二次滤波法、三角级数法、白噪声滤波法、逆傅里叶变换法等[25]。其中,逆傅里叶变换法具有较高的计算精度和很好的通用性,本文采用该方法反演全波段高低不平顺谱。首先指定模拟波长范围为0.002～100 m,空间采样间隔为0.001 m;然后对全波段高低不平顺谱拟合曲线(5阶多项式)的自变量、因变量进行幂运算,得到全波段高低不平顺空间序列的单边谱;最后采用逆傅里叶变换法反演出全波段高低不平顺空间序列。同理,对于中长波高低不平顺谱的反演,首先指定模拟波长范围为2～100 m,空间采样间隔为0.25 m;后续步骤与全波段高低不平顺谱反演的步骤一致。

采用上述方法对全波段高低不平顺谱和中长波高低不平顺谱各反演了总长为1 000 m的时域样本,两次反演采用相同的随机相位信息,见图8(a),200～225 m区段的细部放大图见图8(b)。由图8可以看出,在相同长度范围内,相比于反演的中长波高低不平顺,反演的全波段高低不平顺在时域波形上有了更多的短波起伏,对高低不平顺的刻画也更为细致。反演结果的功率谱见图9。由图9可知,其均在各自反演的波段范围内与高铁无砟轨道高低不平顺全波段谱高度吻合,验证了反演结果的准确性。

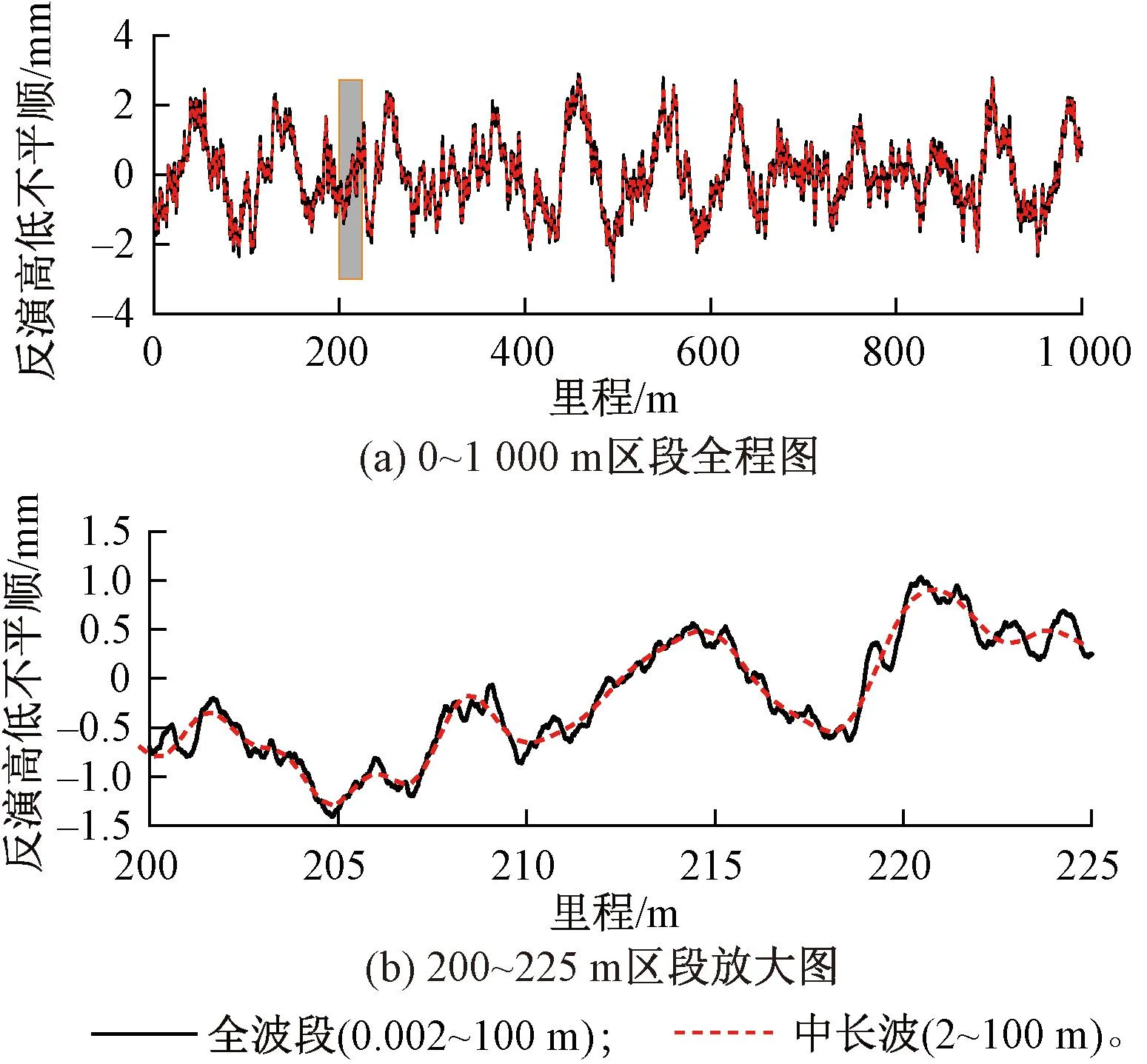
图8 反演的高铁无砟轨道高低不平顺

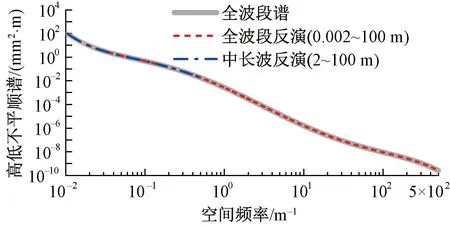
图9 反演的高铁无砟轨道高低不平顺谱

3 全波段高低不平顺对车辆动力学响应的影响

以某高铁中存在钢轨波磨病害的线路区段为例,分析全波段高低不平顺对车辆动力学响应的影响。该区段采用双块式无砟轨道结构,长度为500 m,位于大半径曲线,曲线半径10 000 m。

3.1 全波段高低不平顺的合成方法

首先对波磨测试小车数据和动态检测数据进行里程同步。由于波磨测试小车的有效检测波段为1 m以下,高速综合检测列车的可输出的波段为1.5～120 m,在合成全波段高低不平顺时,取1.25 m作为滤波的截止波长。以该截止波长对波磨测试小车数据高通滤波获取短波高低不平顺;以该截止波长对动态检测数据低通滤波获取中长波高低不平顺。然后将短波和中长波高低不平顺叠加得到全波段高低不平顺,上述3种高低不平顺功率谱和时域波形见图10、图11。图中,L为波长。

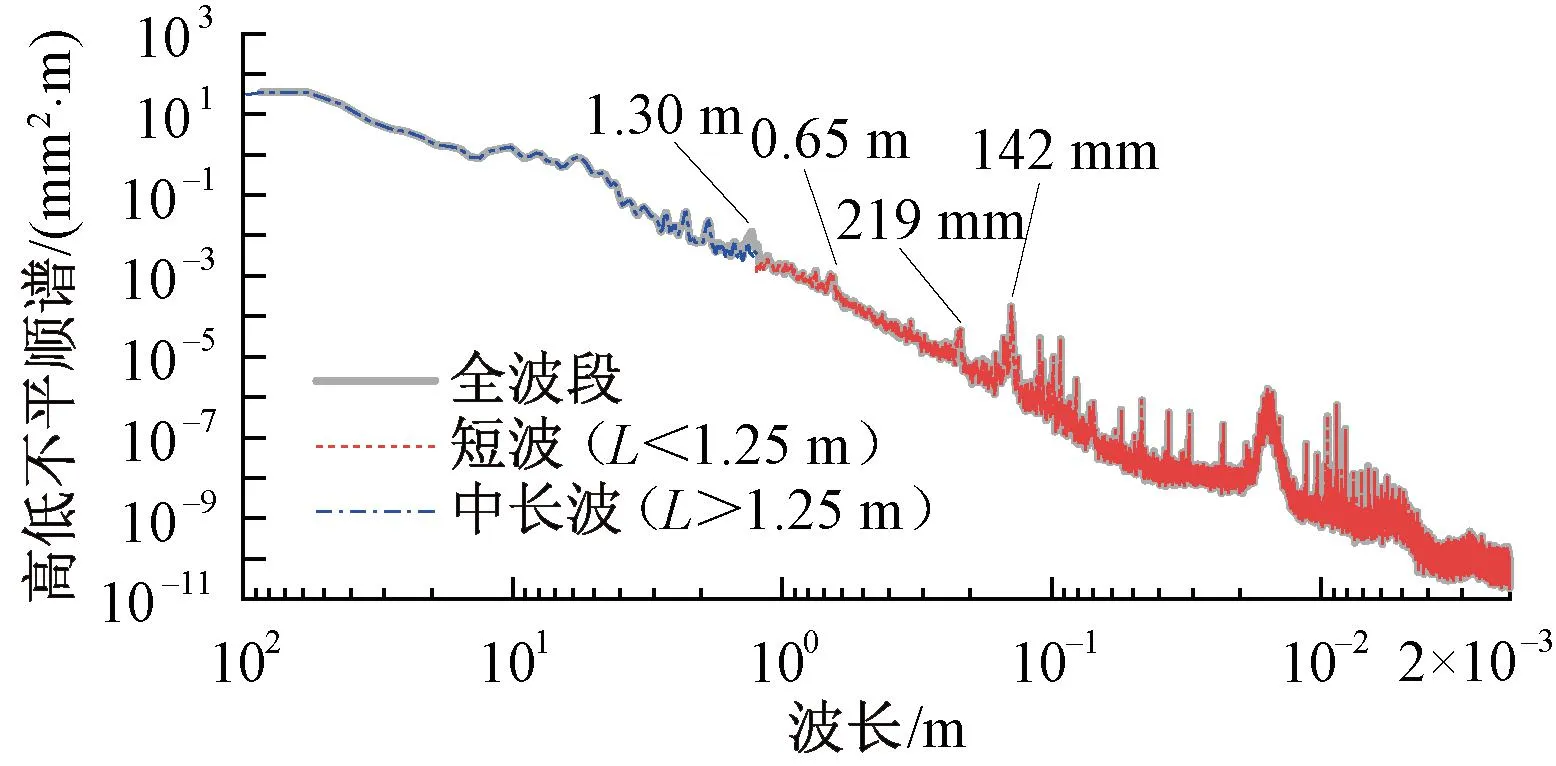
图10 组合全波段高低不平顺谱

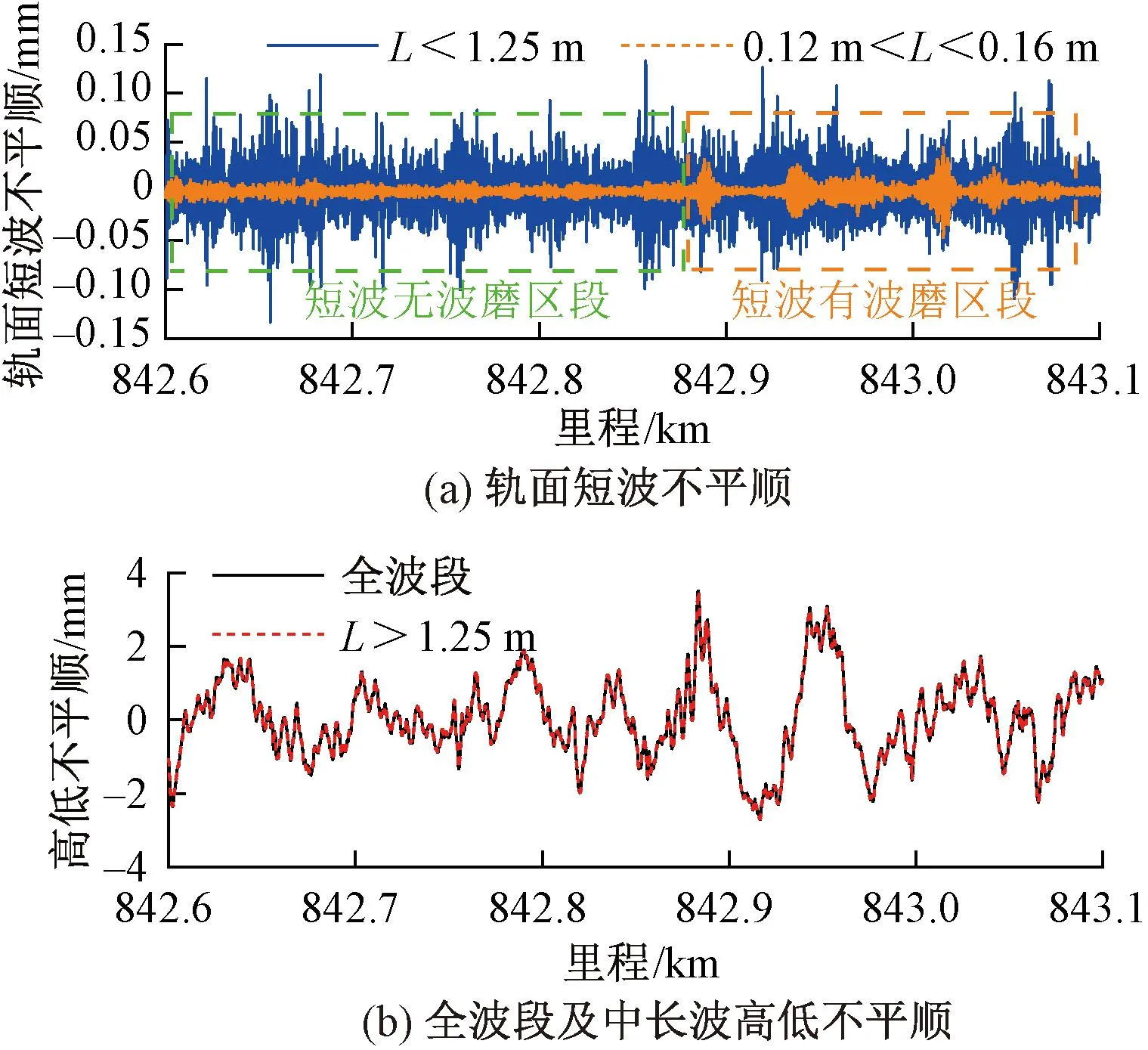
图11 实测全波段高低不平顺

由图10可知,滤波后得到的短波和中长波高低不平顺谱在波长1～2 m之间平滑过渡,验证了该方法和截止频率选取的合理性。在波长1.30、0.65 m处存在明显谱峰,这可能与双块式无砟轨道轨枕间隔0.65 m相关。该区段在142、219 mm等特征波长处存在显著的能量集中,波长为142 m处最为严重,现场复核见图12。由图12可知,该处存在较为显著的钢轨波磨病害。将轨面短波不平顺按0.12～0.16 m带通滤波,结果见图11(a)。由图11(a)可知,该频带内的轨面短波不平顺在里程K842+880—K843+086区段更为显著,最大幅值可达0.047 mm。

图12 现场钢轨波磨病害

3.2 实测车辆动力学响应分析

试验列车为CRH380A型动车组,列车在该区段以302 km/h匀速行驶,对实测的车辆各部件垂向加速度、轮轨垂向力与全波段高低不平顺进行里程同步后开展谱分析,其功率谱见图13、图14。轴箱、构架、车体振动响应以及轮轨垂向力分别约在383、591 Hz出现较为明显的谱峰,由于上述频率成分分别与波长为219、142 mm的轨面周期性短波不平顺引起的冲击频率相符,表明上述谱峰与轨面短波不平顺严重程度相关。其中,轴箱垂向加速度和轮轨垂向力在受轨面短波不良影响的频带550～650 Hz内所携带的能量最大;构架垂向加速度在14～19 Hz 以及受轨面短波不良影响的383 Hz附近表现出的振动响应最为剧烈;车体垂向加速度谱峰最大值出现在128 Hz附近,在其1/2倍频64 Hz附近能量也较为显著。

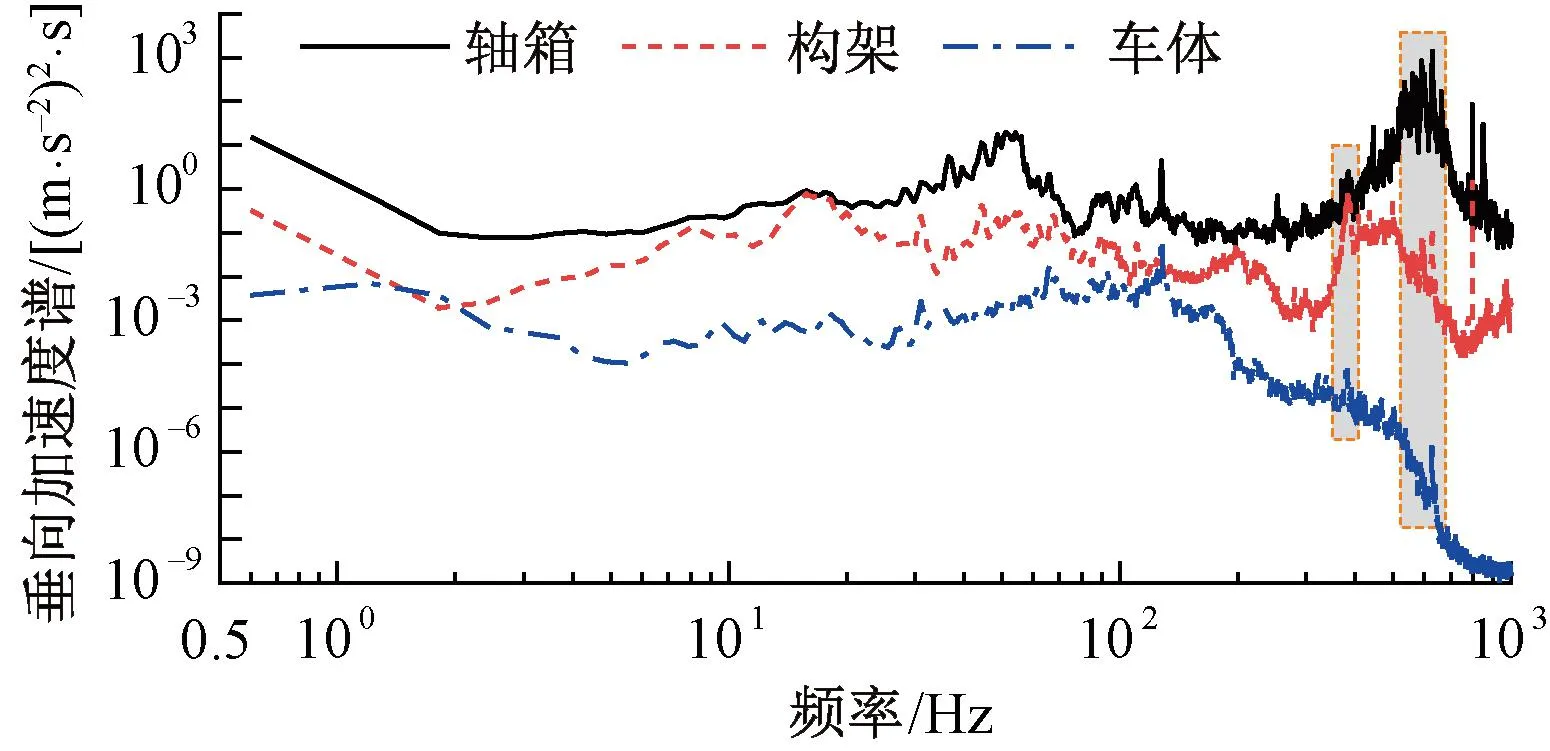
图13 车辆各部件垂向加速度谱

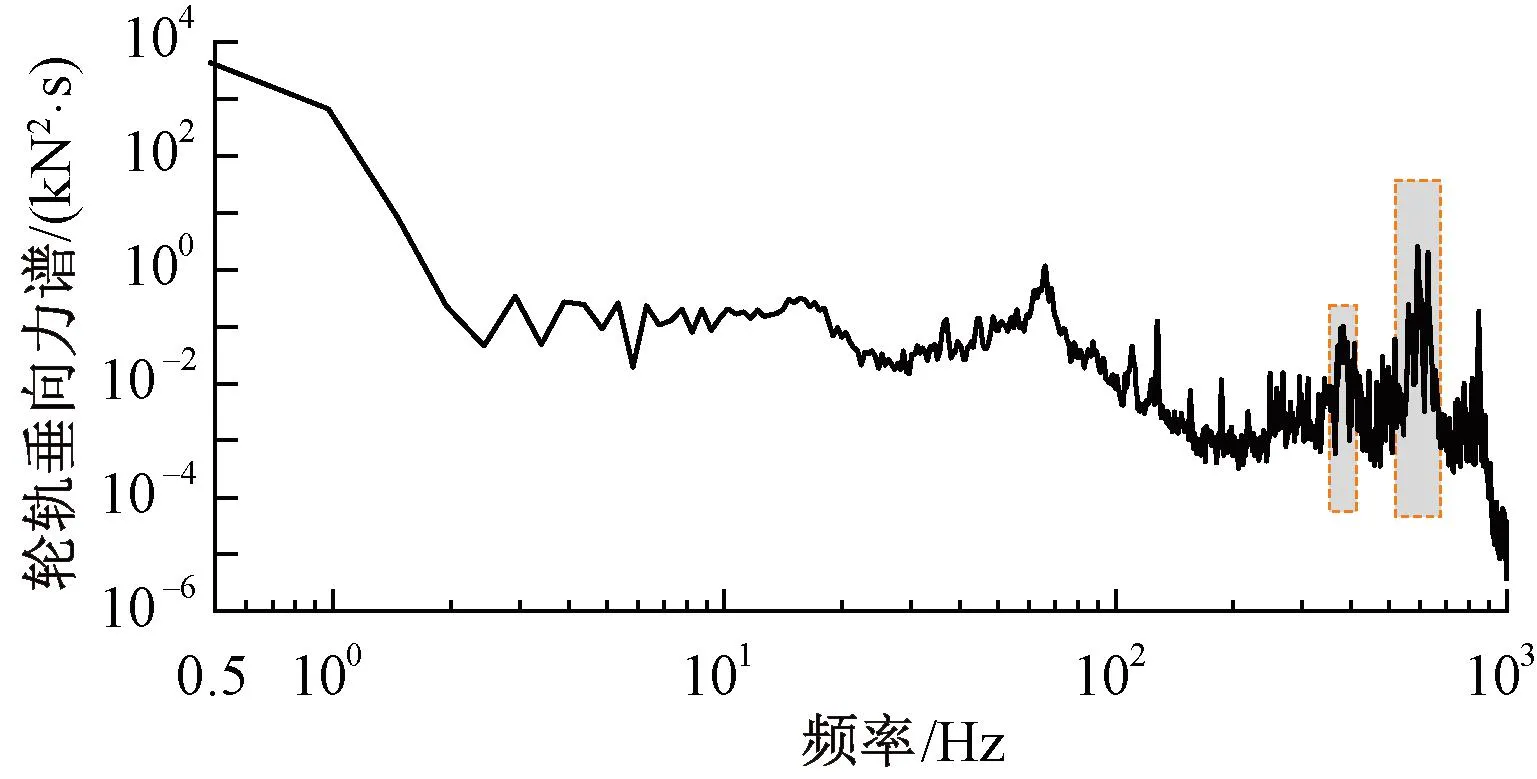
图14 轮轨垂向力谱

为去除高频噪声信号的影响,将实测车辆动力学响应数据进行2 000 Hz低通滤波,再按照截止波长1.25 m分别进行高通和低通滤波,将动力学响应数据分解成短波成分和中长波成分。全波段和中长波车辆动力学响应数据见图15。由图15可以看出,轨面短波周期性成分显著区段对轮轨垂向力和轴箱垂向加速度的影响最为大。为进一步量化全波段高低不平顺对车辆动力学响应的影响,选取线路中有波磨区段与无波磨区段,分别计算高低不平顺、车辆动力学响应的短波和中长波成分的99%分位数,以此表示各个指标的峰值,统计结果见表 3。

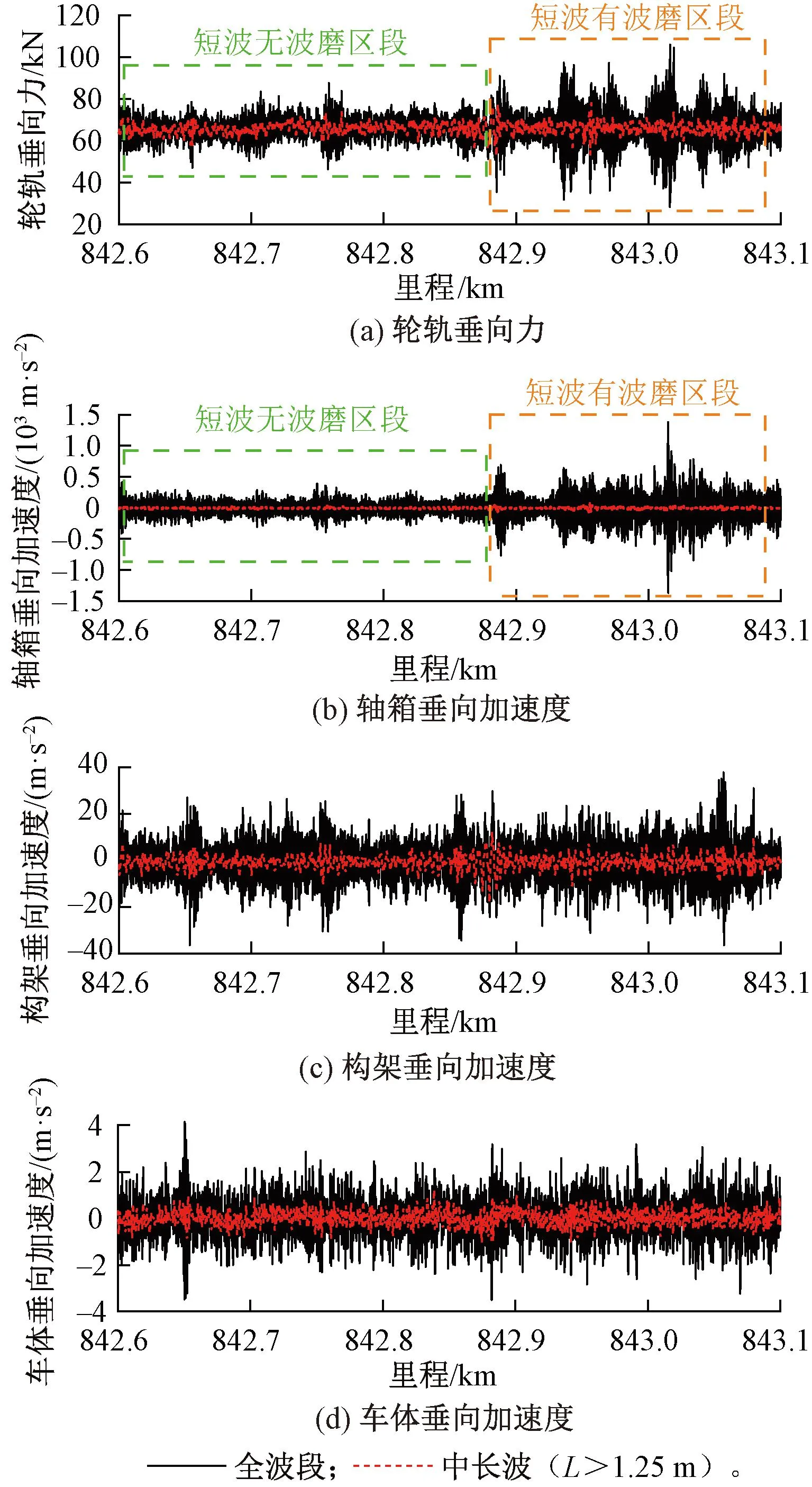
图15 实测车辆动力学响应

由表 3可知,就短波成分统计结果而言,尽管有波磨区段与无波磨区段的短波高低不平顺峰值相当,周期性短波不平顺引起的幅值被淹没在随机性短波不平顺中,但波磨区段轮轨垂向力峰值和轴箱垂向加速度峰值被放大至对照区段的2.2倍,波磨区段构架、车体垂向加速度分别被放大至1.1、1.0倍,说明轨面短波不平顺的周期性成分会显著放大轮轨垂向力和轴箱垂向加速度响应。

通过对比图12与图15进一步发现,虽然短波高低不平顺峰值无论在钢轨波磨区段还是无波磨区段均远小于中长波高低不平顺峰值,短波不平顺在高速行车条件下会显著放大轮轨垂向力以及轴箱、构架和车体垂向加速度等车辆动力学参数,可见在车辆动力响应分析中引入包含短波成分在内的全波段高低不平顺具有重要意义。

4 结论

本文基于多条无砟轨道高铁的轨面粗糙度与动态轨道高低不平顺实测数据,提出轨面短波不平顺谱和全波段高低不平顺谱的表达公式,并在基础上结合高速综合检测列车线上运行试验,分析高铁全波段高低不平顺对车辆动力学响应的影响。主要结论如下:

1)提出采用两段幂函数拟合高铁无砟轨道轨面短波不平顺谱。上限谱幅值整体小于Stao谱的上限谱;当波长小于0.025 m时,上限谱幅值大于Stao谱的下限谱;当波长小于0.045 m时,上限谱幅值大于王澜谱;其余波段上限谱幅值小于Stao谱的下限谱和王澜谱。均值谱幅值整体小于Stao谱;当波长小于0.006 m时,均值谱幅值大于王澜谱;其余波段均值谱幅值小于王澜谱。下限谱幅值均小于Stao谱和王澜谱。

2)提出采用对数坐标系下的5阶多项式拟合高铁无砟轨道全波段高低不平顺谱,2 m以上波长成分采用动检车测试数据,1 m以下波长成分采用波磨小车测试数据,全波段高低不平顺谱在波长1～2 m之间实现了中长波和短波成分的平缓过渡。

3)相比于反演的中长波段高低不平顺,由全波段高低不平顺谱反演的时域波形具有短波起伏特征,对高低不平顺的刻画更为细致。

4)高速行车条件下,无论线路中是否存在钢轨波磨病害,短波高低不平顺对轮轨垂向力以及轴箱、构架和车体垂向加速等车辆动力学参数均存在显著影响,全波段高低不平顺的引入对车辆动力学响应分析非常重要。