基于GPD理论和百分位数阈值法的轮轨力极值估计与动力系数研究

郭 杰，杨荣山，谭 斌

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.中铁二十三局集团有限公司，四川 成都 610072)

在设计和检算无砟轨道结构时,需要确定与设计速度匹配的列车荷载设计值及其动力系数[1-2]。我国对高速铁路的研究、优化不断深入,而随着列车速度的提高,轮轨相互作用势必加剧。作为一种致力于少维修甚至不维修的轨道结构,无砟轨道的应用越来越广泛。无砟轨道虽然可有效保证线路的平顺性,但其造价高昂亦是不容忽视的问题。如何在保持无砟轨道良好的服役性能和提高经济性之间取得平衡是一个难题,轮轨力动力系数的取值对此有一定影响。因此,合理的轮轨力动力系数对进一步优化无砟轨道结构设计和应用推广意义重大。

高速铁路的建设也引起学者对高速铁路轮轨力动力系数的研究。对于高速铁路,一般以脉冲激励下的轮轨力来确定动力系数,主要考虑扁疤和焊接接头不平顺的激励结果,如日本采用40 mm长度的扁疤确定轮轨力动力系数为3[3]。经过计算比较,TB 10621—2014《高速铁路设计规范》[2]认为扁疤激励结果较焊接接头不平顺的大。其中,列车速度为250 km/h的动力系数为2.5,列车速度为300、350 km/h的动力系数均为3。近年来,我国提出将高速铁路设计速度提高至400 km/h,并进行相关关键技术的研究,如文献[4-5]分析了焊接接头不平顺和扁疤激励下的轮轨力动力系数。

实际上,列车荷载设计值也可以是一定保证率下的最大轮轨力,可以计算含短波的不平顺激励下的轮轨力最大值,这在本质上属于极值估计的范畴。早期,文献[6-7]采用人工构造短波并叠加中长波不平顺的方法,得到了高速铁路有砟轨道轮轨力动力系数。

极值理论已在气象水文、风险管理和公路桥梁等领域得到广泛应用[8-10]。本文采用GPD理论进行轮轨力的极值估计。GPD理论是基于超越阈值法的极值估计方法,阈值的选取是难点,目前学术界难以统一。传统的平均超出量函数法和Hill图法主观依赖性大[11],Thompson等[12]提出的自动阈值选取方法则在后处理编程时较为复杂,计算效率也不高。为此,有学者直接采用某一百分位数作为阈值,该方法简单实用,后处理编程简单,计算效率较高。如杨萌等[13]以99%分位数作为阈值,用GPD理论拟合了成都经济区日降水量数据。张昕怡等[14]采用百分位数选取阈值,用GPD理论拟合中国格点化日降水量数据,认为不同工况下百分位数阈值取值应不同。

本文基于我国目前最新的轨道不平顺研究成果和GPD理论,结合百分位数阈值法,系统分析了轮轨力极值估计方法,确定了GPD理论在轮轨力极值估计时的具体过程和方法,研究成果扩展了GPD理论的应用途径。最后,得到了与无砟轨道结构设计寿命相匹配的轮轨力动力系数,为无砟轨道结构设计和检算提供依据。

1 动力学模型和轨道不平顺

本文采用CRH2和CRH380A动车组,采用CRTSⅢ型无砟轨道。动力系数模型中,车辆包含7个刚体,一个车体,两个转向架和4个轮对。无砟轨道则采用三层叠合梁模型,各层之间由弹簧阻尼元件连接。

为方便比较,本文同样计算了扁疤和焊接接头不平顺激励下的轮轨力,以往的研究中扁疤长度均取40 mm。现在,我国在日常动车组维修中已将扁疤长度限制在30 mm以内[15]。因此,本文扁疤长度取30 mm。焊接接头模型参见文献[4,16],但这与我国高速铁路焊接接头不平顺不相符。因此,应采用由我国高速铁路焊接接头实测资料确定的焊接接头不平顺模型,实测焊接接头模型参见Gao等[17]的实测结果,焊接接头不平顺包括凸接头和凹接头,且焊接凸接头不平顺包括两种,本文分别记为第Ⅰ类和第Ⅱ类。

对于随机不平顺,为得到轮轨力动力系数,需考虑短波不平顺。前期一直没有可以准确表征中国高速铁路不平顺特点的全波段不平顺谱,故文献[6-7,18]多是将短波和中长波不平顺进行叠加。杨飞等[19]对我国高速铁路随机短波不平顺进实测,并与中长波不平顺进行连接,采用多项式拟合,实现在波长1～2 m的搭接波段的顺滑连接,从而得到了全波段不平顺谱,见图1。

图1 全波段不平顺谱

波长范围为2～100 m,可准确表征我国高速铁路全波段不平顺的特点,即

lg[S(f)]=a0+a1·lg(f)+a2·lg(f)2+a3·lg(f)3+

a4·lg(f)4+a5·lg(f)5

( 1 )

式中:lg[S(f)]为轨道不平顺功率谱密度,mm2·m;lg(f)为空间频率,1/m;a0,…,a5均为拟合系数,具体值见表1。

表1 无砟轨道全波段不平顺谱拟合参数

2 GPD理论概述

( 2 )

( 3 )

( 4 )

( 5 )

( 6 )

本文采用百分位数法选取阈值,即直接将某一百分位数作为阈值。

3 扁疤和焊接接头不平顺激励结果

扁疤和焊接接头不平顺激励下,不同列车速度下,CRH2和CRH380A动车组轮轨力和动力系数计算结果见表2。表2中,轮轨力与静轮载之比记为列车荷载设计值动力系数;“/”左、右侧分别为CRH2、CRH380A动车组的计算结果,后文相同,不再赘述。CRH2、CRH380A动车组静轮载分别为67.0、59.1 kN。

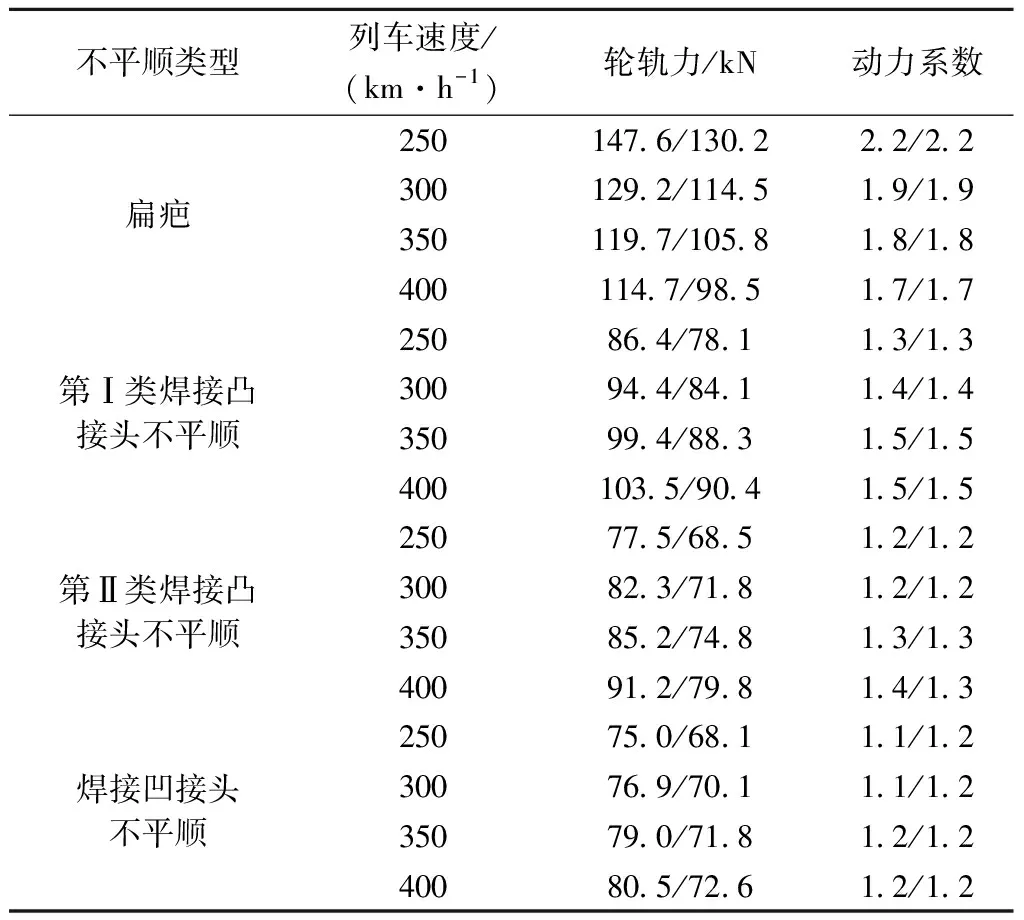
表2 扁疤和焊接接头不平顺激励下轮轨力和动力系数结果汇总

由表2可知,焊接接头激励下的动轮轨力和动力系数远小于扁疤的结果。焊接接头不平顺激励下的动力系数随着列车速度的增大略有增大,但均不超过1.5。而扁疤激励下,动轮轨力和动力系数逐渐减小,这与一些文献[4]研究结论一致。此外,由于 CRH2动车组的簧下质量大于CRH380A动车组,故而CRH2动车组的轮轨力较CRH380A动车组大,但两种动车组的列车荷载动力系数却基本相当。由对比结果可知,当采用脉冲激励计算动力系数时,应选择扁疤。

我国在制定TB 10621—2014《高速铁路设计规范》[2]时,车辆采用CRH2动车组,扁疤长度为40 mm,其最大轮轨力采用速度较低时的结果。但我国高速铁路均为客运专线,列车运行速度较高,正常运营速度均超过250 km/h,部分达到甚至超过350 km/h。若采用较低速度时的轮轨力来确定动力系数则与列车实际运营情况不符。可见,TB 10621—2014《高速铁路设计规范》[2]存在一定缺陷。

4 全波段不平顺激励结果

4.1 分簇对极值估计的影响

工程上将超越率为1×10-6时的值作为极值[24],故本文仿真得到样本总量为1×106个的轮轨力,并将1×106个样本中的最大值视为极值的真实值。列车速度为250～400 km/h时,CRH2动车组的轮轨力极值的真实值分别为137.2、144.5、157.9、162.8 kN,CRH380A动车组的轮轨力极值的真实值则分别为125.0、135.0、141.5、152.0 kN。

采用GPD理论进行极值估计时,样本应相互独立。可对样本进行筛选来提高样本之间的独立性,进而提高极值估计的精度。将样本分成若干簇,只取每簇中的最大值而舍弃其余值,可提高样本的独立性[25]。若样本量为n,每簇中的样本量为Δn,则分簇的个数Nd为

( 7 )

一般地,Δn不宜太大,否则Nd太小,实际用于计算的样本太少,Δn太小则不能有效提高样本之间的独立性。需要注意是,分簇的个数Nd须为正整数,故Δn应能被n整除。本文选取的Δn取值分别为20、25、40、50、80、100、125、200、250、400、500、625、1 000,为方便叙述,将其记为D集。

为分析Δn取值对提高样本之间独立性的效果,可绘制奇、偶轮轨力散点图。散点图分别以奇、偶轮轨力为横、纵坐标。以CRH380A动车组为例,列车速度为350 km/h时,部分Δn的奇、偶轮轨力散点图见图2。图2中,Δn=1表示未对样本进行分簇。

图2 奇、偶轮轨力散点图

由图2可知,未对样本进行分簇时,偶数轮轨力随奇数轮轨力的增大表现出增大趋势,表明未分簇时奇、偶轮轨力之间独立性较差。当对样本进行分簇时,奇、偶轮轨力散点图分布较为分散,表明奇、偶轮轨力之间独立性较强。可见,通过分簇可有效提高样本之间的独立性。

样本量取5×105个,Δn取值为D集,百分位数阈值的取值范围为50%～98%。由于计算工况较多,且计算结果类似,本文以CRH380A动车组速度为300 km/h时的结果进行分析,部分Δn的轮轨力极值和误差随百分位数阈值的变化见图3。

图3 轮轨力极值和误差随百分位数阈值的变化

由图3可知,未对样本分簇时,轮轨力极值估计值随百分位数阈值的增大而增大,但始终小于真实值。可见,未对样本分簇时,样本之间的相关性严重影响轮轨力极值估计的效果。从工程设计角度来讲,一般需要得到略大于真实值的估计值,如超过真实值10%以内,未对样本分簇无法实现这一目的。当对样本分簇时,不同Δn的轮轨力极值估计值随百分位数阈值的增大无明确的规律可循,表现出较强的离散性,但对样本分簇可得到略大于真实值的轮轨力极值估计值。

Δn取不同值时,均存在合理的百分位数阈值。Δn取50、100、500时,不同列车速度下CRH2和CRH380A动车组合理的百分位数阈值见表3。

表3 不同列车速度下合理的百分位数阈值

由表3可知,Δn取不同值时,不同列车速度下合理的百分位数阈值也不相同。其中,Δn为50时,不同列车速度下,CRH380A动车组存在重合的百分位数阈值为76%～79%,CRH2动车组则不存在。而当Δn为100、500时,不同列车速度下CRH2和CRH380A 动车组均不存在重合的百分位数阈值。可见,对于不同的动车组,Δn取不同值时,不同列车速度下难以得到统一合理的百分位数阈值,通用性差,限制了百分位数阈值和GPD理论在轮轨力极值估计中的应用。

4.2 基于形状参数的极值筛选方法

由4.1节计算结果可知,对样本分簇并结合百分位数选取阈值可得到与真实值十分接近的轮轨力极值,若能找到一种方法将这些与真实值十分接近的轮轨力极值筛选出来,就能解决对百分位数阈值依赖的难题。本节通过分析轮轨力极值估计值与GPD理论形状参数的关系,提出了基于形状参数的轮轨力极值筛选方法。

以Δn取50、80、250和1 000为例,不同列车速度v下,CRH2和CRH380A动车组的轮轨力极值估计值与GPD理论形状参数的关系分别见图4和图5。

图4 轮轨力极值估计值与GPD理论形状参数的关系(CRH2动车组)

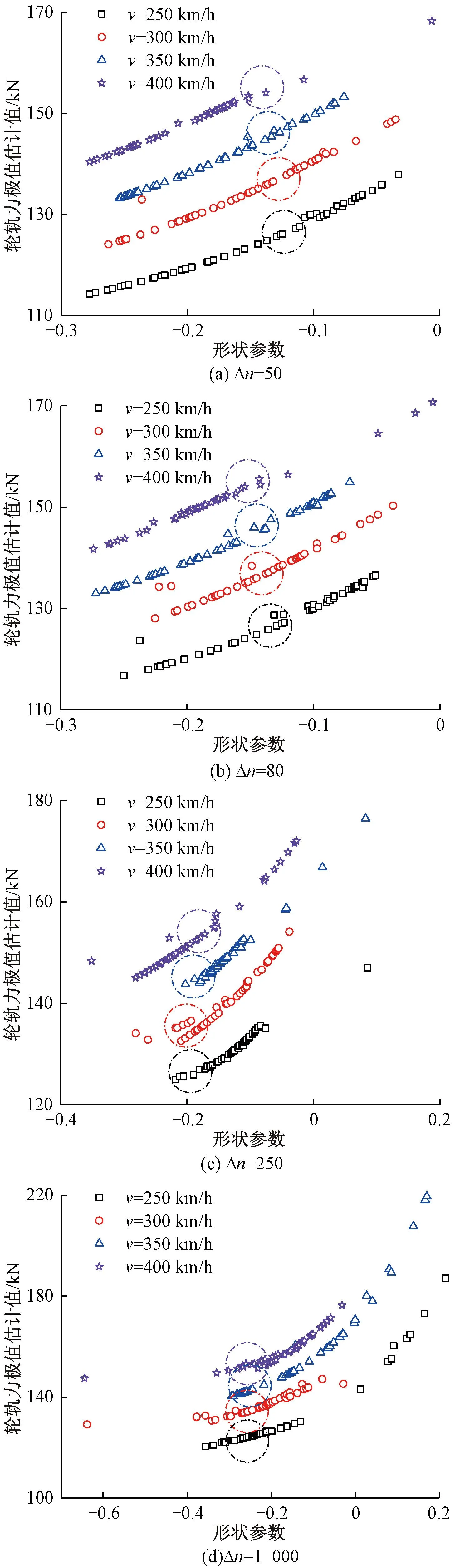
图5 轮轨力极值估计值与GPD理论形状参数的关系(CRH380A动车组)

图4和图5中,圆圈内的散点图可大致代表与真实值较为接近的轮轨力极值估计值。对一个确定的Δn,当轮轨力极值估计值与真实值较为接近时,GPD理论的形状参大致分布在一个确定的区间内,即当Δn取某一个值时,可通过形状参数区间来筛选与轮轨力真实值较为接近的轮轨力极值估计值。如当Δn=250时,由图4(c)和图5(c)可知,当轮轨力极值估计值与真实值较为接近时,CRH2和CRH380A动车组的形状参数均可取-0.22～-0.15。

但对于CRH2和CRH380A动车组,当Δn取D集时,并非所有的Δn取值都可以确定一个重合的形状参数区间,使得轮轨力极值估计值与真实值较为接近,如Δn取1 000时,对于CRH380A动车组,由图5(d)可知,当形状参数取-0.30～-0.20时,轮轨力极值估计值与真实值较为接近;但对于CRH2动车组,由图4(d)可知,不存在重合的形状参数区间使得不同列车速度的轮轨力极值估计值与真实值都较为接近。当Δn取D集时,经进一步计算,当轮轨力极值估计值与真实值较为接近时,满足不同动车组和列车速度的合理的Δn取值及其对应的形状参数区间见表4。

表4 合理的Δn取值及对应的形状参数区间

一般地,由表4中Δn取值及对应的形状参数区间可筛选得到多个轮轨力极值估计值,这些轮轨力极值略大于或略小于真实值,可取其均值作为最终的轮轨力极值估计值以降低离散性。由表4中的参数所确定的最终的轮轨力极值估计值见图6。

图6 最终的轮轨力极值估计值

由图6可知,由表4中的参数所确定的最终的轮轨力极值估计值略大于轮轨力真实值,误差可控制在5%以内,满足工程要求。以CRH380A动车组列车速度为300 km/h为例,部分Δn的轮轨力超出量累计分布函数见图7。

图7 轮轨力超出量累计分布函数

由图7可知,轮轨力超出量经验累计分布函数和理论累计分布函数吻合良好,两者基本重合,相关系数分别达到0.999 8和0.999 7,表明GPD理论对轮轨力拟合效果很好。其他工况计算结果类似,不再赘述。以上分析表明,样本量取5×105个,按照表4中的参数进行轮轨力极值估计效果较好。

4.3 样本量的影响

本节分析样本量对轮轨力极值估计的影响,样本量取3×105～5×105个。以Δn取100时的计算结果为例,不同列车速度下轮轨力极值估计值随样本量的变化见图8。

图8 轮轨力极值随样本量的变化

由图8可知,样本量取3×105～5×105个时,不同列车速度下,CRH2和CRH380A动车组的轮轨力极值估计值随样本量的增大表现出一定的波动,但离散性并不显著,轮轨力极值估计值都略大于真实值。此外,经计算发现,对于某些Δn取值,当样本量较小时存在无解的情况,这主要由于当样本量较少而Δn取值较大时,导致真正用于计算的数据较少,使计算结果存在不确定性。为保证样本量取3×105～5×105个时均存在结果,不应在表4中取太大的Δn。经分析,表4中去除较大的Δn后,最终给出合理的Δn及对应的形状参数区间见表5。

表5 合理的Δn取值及对应的形状参数区间

为降低轮轨力极值估计的离散性,本文取样本量为3×105～5×105个的轮轨力极值估计值的均值作为最终的轮轨力极值估计值,得到的CRH2和CRH380A动车组轮轨力极值估计值及与真实值的误差分别见表6、表7。

表6 CRH2动车组的轮轨力极值估计值及误差

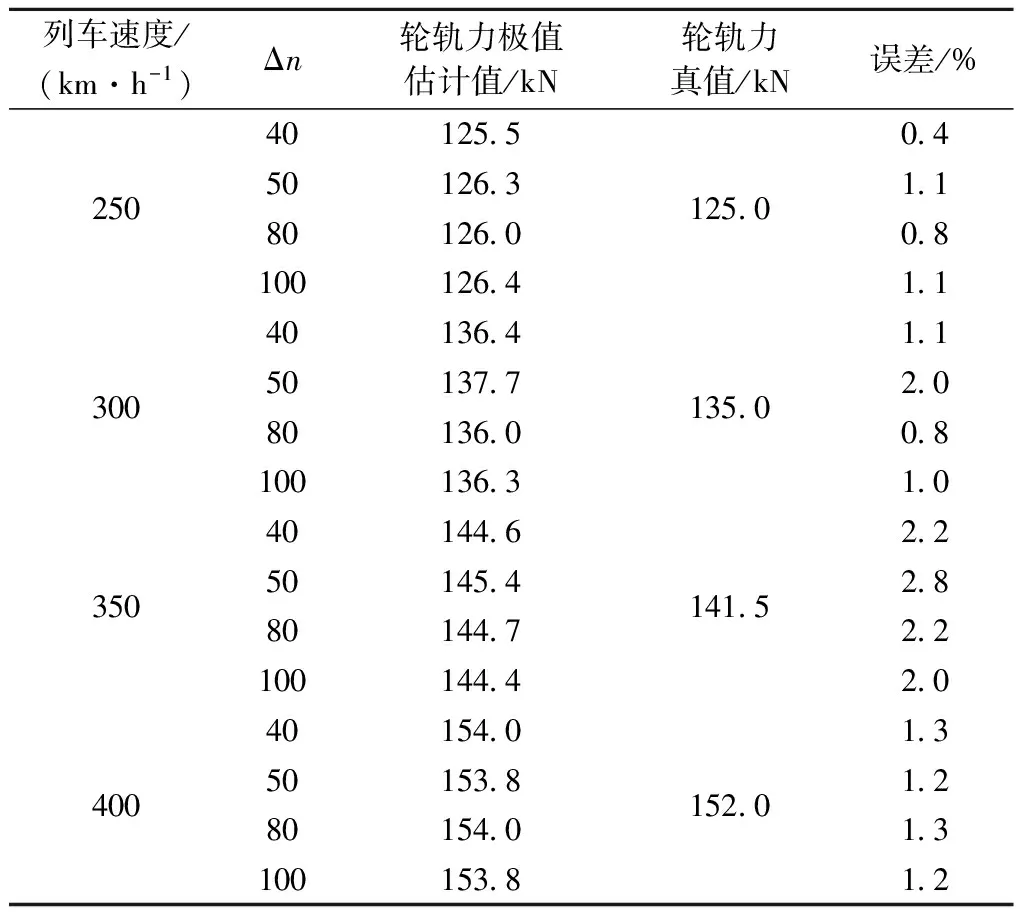
表7 CRH380A动车组的轮轨力极值估计值

由表6和表7可知,轮轨力极值估计值均略大于轮轨力真实值,且误差控制在5%以内,满足工程要求。可见,样本量取3×105～5×105个时,按照表5中Δn及对应的形状参数区间取值,轮轨力极值估计值效果较好,精度较高。本文推荐的合理的样本量为3×105～5×105个,百分位数阈值为50%～98%,且以轮轨力极值估计值的均值作为最终的轮轨力极值估计值。

4.4 轮轨力动力系数

式( 4 )中,超越率为1-p。为了得到无砟轨道结构设计寿命相匹配的动力系数,需确定超越率1-p。针对未来我国高速铁路的发展趋势,行车密度取190对/d,动车组考虑16节编组[26]。无砟轨道结构设计寿命为60 a,则荷载作用次数N为

N=60×365×190×16×4=2.66×108

( 8 )

超越率1-p为

( 9 )

基于4.3节的结论,列车速度为250～400 km/h时,按照表5中Δn及对应的形状参数区间取值,设计寿命为60 a的轮轨力极值估计值和动力系数见表8。

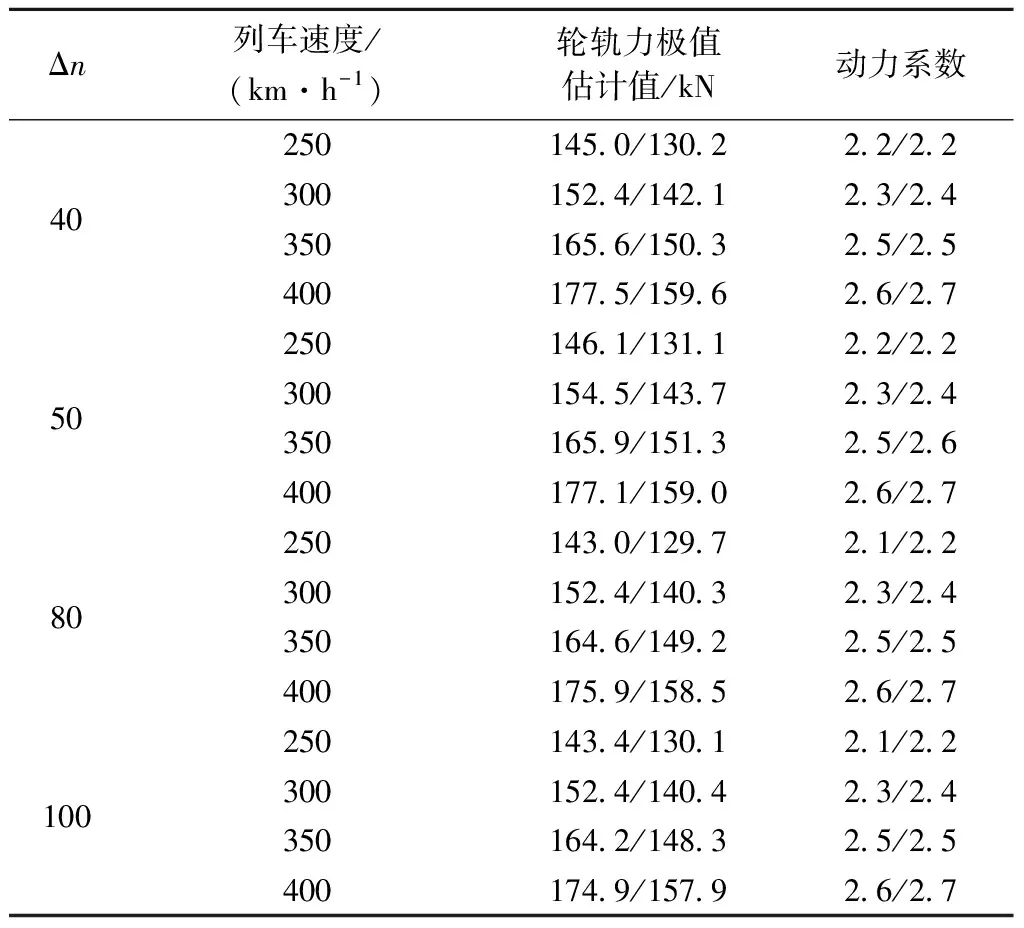
表8 设计寿命为60 a的轮轨力极值估计值及动力系数

由表8可知,Δn取不同值时,CRH2和CRH380A动车组轮轨力极值估计值和动力系数随列车速度的增大基本呈线性增大,且同一速度下的CRH2和CRH380A动车组列车荷载设计值动力系数相差不大。由于轮轨力主要受簧下质量的影响,CRH2和CRH380A动车组的簧下质量分别为2、1.752 t,可代表中国目前动车组的簧下质量水平,这表明在全波段不平顺激励下,动力系数受簧下质量影响较小。

一般地,由表8可知,列车速度为250～400 km/h的动力系数可分别取2.2、2.4、2.6和2.8,动力系数α与列车速度v的拟合关系为

α=1.2+0.004v

(10)

文献[27]的实测表明,列车速度为350 km/h时,轮轨力最大值为156.6 kN,与本文结果较为接近,在一定程度上验证了本文结论的可靠性。

将全波段不平顺和第3节扁疤激励下的动力系数计算结果进行对比可知,列车速度为250 km/h时,两者的计算结果相差不大,均为2.2左右。而列车速度为300～400 km/h时,全波段不平顺激励得到的动力系数大于扁疤激励下的结果,此时,动力系数应取全波段不平顺激励下的结果。此外,由式(10)可知,采用全波段不平顺激励时,动力系数随列车速度的增大线性增大,而采用扁疤激励时动力系数随列车速度的增大而减小。可见,采用全波段不平顺激励计算动力系数更合理。

5 结论

为得到列车荷载设计值动力系数,本文基于GPD理论和百分位数阈值法,系统分析了GPD理论在轮轨力极值估计中的应用方法,得出以下结论。

1)采用百分位数法确定阈值时,为提高样本之间的独立性和轮轨力极值估计的精度,应对样本进行分簇。

2)为避免对百分位数阈值的依赖,提出了基于形状参数筛选法的轮轨力极值估计,确定了每簇样本量大小和形状参数区间。

3)推荐的样本量为3×105～5×105个,百分位数阈值为50%～98%,且以轮轨力极值估计值的均值作为最终的轮轨力极值估计值。

4)应采用全波段不平顺激励计算列车荷载设计值动力系数,列车速度为250～400 km/h时,推荐的动力系数分别为2.2、2.4、2.6和2.8。