基于轨道结构高差特征值的CRTSⅡ型板离缝定量检测方法

王广琦，毛庆洲，夏梦璇，穆远博，施以旋

(武汉大学 遥感信息工程学院，湖北 武汉 430079)

目前,我国高速铁路已建成的总里程数已经超过4.2万 km,投入运营的时间已经超过10年。无砟轨道得益于结构稳定性好和使用寿命长等优点被大量应用于高速铁路建设中[1-2]。由于长期受列车的高频冲击作用和复杂自然环境的影响,离缝病害也逐步显现[3-4]。轨道板变形上拱进一步加大了离缝量,直接影响着列车的安全运行[5]。大量调研结果表明,在持续高温的季节,部分层间病害的离缝量最大超过了10 mm,导致列车只能限速通行[6]。

当前,高速铁路无砟轨道离缝病害的检测需要使用传统的测量仪器,主要包括探地雷达法、超声波法和冲击回波法等。探地雷达主要通过检测材料诱电性能的不连续性,利用高频电磁波在不同介质面上的反射来判断结构内部的伤损分布情况[7]。舒志乐等[8]建立无砟轨道的物理模型,利用探地雷达实现了空洞病害检测和三维正演模拟。冲击回波法利用冲击装置产生应力波,对波形进行时频域分析来判断结构中的病害。Xu等[9]在仿真模型中预设了伤损,研究使用冲击回波法检测无砟轨道典型损伤的可行性,结果表明冲击面和损伤面之间的多波反射在频谱中产生了一个大振幅的峰值,其频率与损伤的深度相对应。田秀淑等[10-11]提出一种基于P波特性的病害回波特征提取方法,实现了层间病害的检测与识别,验证了基于瞬态弹性波法检测层间病害的可行性。超声波法基于材料病害导致的声学性能差异,对超声波传播波形的反射情况进行分析,实现对材料内部病害的检测。李再帏等[12]建立Lamb波在CRTSⅡ型板式无砟轨道中的传播模型,验证了特定模态下Lamb波可以实现无砟轨道层间伤损的定量分析。Zhu等[13]建立高速铁路无砟轨道的多层声速模型,将一种基于均方根合成孔径聚焦技术的超声成像方法用于轨道结构病害的检测中。Chen等[14]利用空气耦合的超声波传感器,基于导波能量泄漏原理,实现了对轨道板下空隙缺陷的定量表征和成像。张利刚等[15]将机械光栅式测缝计应用到无砟轨道板上拱检测中,试验结果表明该方法能够有效实现轨道板的上拱定量监测。现有无损检测方法能很好的实现轨道板离缝状态的检测,但在实际应用中的测量速度较低,一般只适用于定点或短距离内的检测。除此之外,动检列车通过测量轨道线形的变化也可以判断轨道是否存在离缝病害。Li等[16]针对高速铁路轨道板翘曲变形病害的快速检测,基于高速轨检列车采集到的轨道几何测量数据,提出一种自动检测板块变形的方法,在时域和频域上分析了轨道垂直不平顺的特征,实现了离缝病害的快速检测。李晨钟等[17]基于动检列车采集的不平顺数据,使用加权小波能量作为轨道板变形的劣化指标,使用长短时间记忆模型对计算得到轨道板变形的劣化指标的进行滚动预测,判断轨道是否发生变形类的病害。杨飞等[18]研究轨道板离缝上拱引起的轨道几何参数及波形变化特征,建立了轨道板上拱识别和预警模型,运用了频谱分析、变化识别和趋势识别等多种方法实现了轨道离缝区段的识别。Ma等[19]将采集到的一维动检数据转化为二维图像数据,使用深度学习目标检测的方法识别异常数据,结果表明该方法可以有效地检测轨道板上拱引起的结构损伤。但轨检列车的测量成本较高且难以直接定量的测出离缝的长宽数据,一般用于线路的定期普检,仍需要人工配合检查。

综上所述,传统的检测方法不适用于高速铁路线路的全面普检,而基于动检数据的检测方法目前难以准确地计算离缝的长宽信息。针对以上问题,本文研发了一套无砟轨道层间离缝病害检测系统,提出了一种基于轨道结构高差特征值的离缝病害定量检测方法。通过移动测量的方式采集轨道板-支承层之间的相对高差特征值,以轨枕位置作为多周期数据对比的里程基准,精确计算离缝的高度和长度。

1 技术路线及检测系统构建

1.1 技术路线

技术路线见图1。

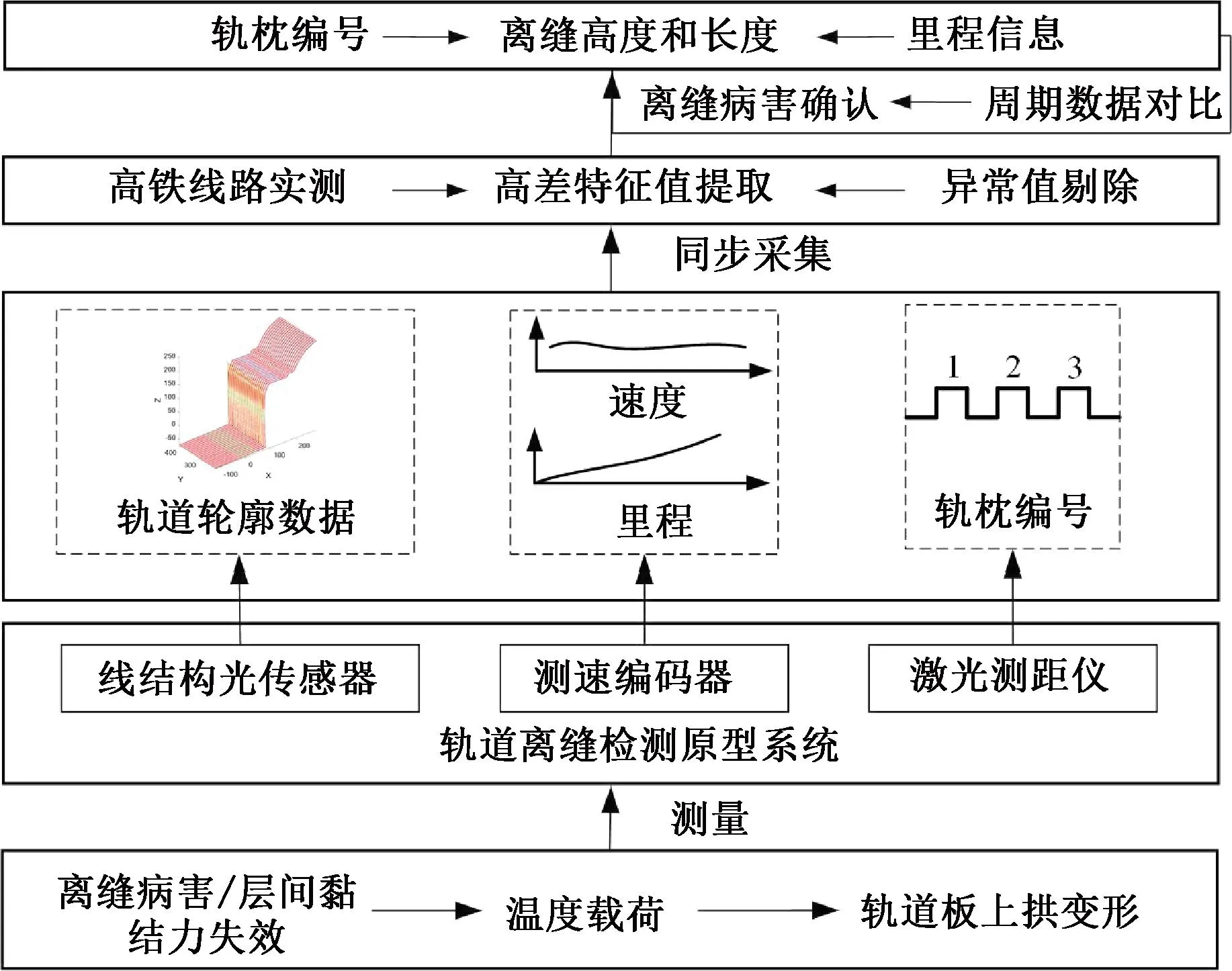
图1 技术路线

由图1可知,当轨道板与砂浆层之间的黏结力失效而发生分离时,轨道板在温度载荷的作用下会上拱变形,从而导致轨道板表面和支承层表面之间的相对高度差发生明显变化。通过对比离缝病害发生前后轨道结构特定位置的几何特征变化,可以实现层间离缝病害的定量检测。因此,本文将轨道板表面和支承层表面间的相对高差值简称为轨道结构高差特征值。据此,实现轨道离缝病害定量检测的关键在于:①轨道结构高差特征值的重复测量精度;②高差特征值里程定位的准确性。为此,本文构建了轨道离缝检测原型系统,同时采集轨道的轮廓数据并记录载体通过的轨枕编号,通过对比不同周期轨道结构高差特征值的变化计算离缝的高度和长度,实现无砟轨道离缝病害的定量检测。此外,传统的测量方法依赖里程信息进行位置匹配和病害定位,但在长距离测量中容易出现里程定位误差累计累积的问题。因此,本文以每个轨枕为测量单位,对测量范围内的轨枕依次编号,建立轨枕编号与轨道结构高差数据之间的特定对应关系,确保不同周期测量数据的精确匹配,从而实现离缝的定量检测。

1.2 离缝检测原型系统构建

离缝检测原型系统见图2。由图2可知,离缝检测原型系统采用模块化设计,易于现场的组装和调试。两个线结构光传感器可随载体的推行持续获取轨道结构表面的高精度轮廓数据;激光测距仪实时测量载体距离轨道板表面的距离,并用于对轨枕编号的累计计数;编码器实时测量载体推行的速度并计算运动的里程。中控计算机的主要功能是管理和协调各测量传感器有序运作,同时负责存储测量数据。检测作业完成后,解析测量数据即可获得离缝病害的定量检测结果。系统的检测效率与轨道小车的推行速度有关,一般可实现5～7 km/h的检测速度。

图2 离缝检测原型系统

两个线结构光传感器的扫描频率最高可达5 000 Hz,重复测距精度为0.02 mm。利用线结构光传感器可以获取轨道侧面的几何轮廓数据。但轨道两侧存在障碍物,线结构光传感器无法直接从侧面垂直扫描轨道结构。综合考虑安装的可行性和使用的可靠性,采用图3所示的测量方式,使线结构光传感器以一定的倾斜角度扫描轨道板、砂浆层和支承层的交界处,获取轨道侧面的轮廓数据。

1.3 基于多传感器同步控制的轨道轮廓数据定位方法

为解决里程定位累积误差导致多周期测量数据无法对准的问题,本文采用多传感器同步控制技术。以每个轨枕的位置作为里程定位的基准,对测量区域内的轨枕进行顺序编号,从而建立轨道轮廓数据和轨枕位置之间的对应关系。

移动测量系统中各传感器同步的方式主要分为距离触发同步和时间触发同步。其中,距离触发同步通过测量载体的行驶距离来控制传感器的数据采集。相较于时间触发同步的方式,距离触发同步简单可靠,不依赖复杂的硬件设备或时钟同步机制,能适应不同的测量场景和速度变化。检测系统中各传感器与中控计算机的连接方式见图4。

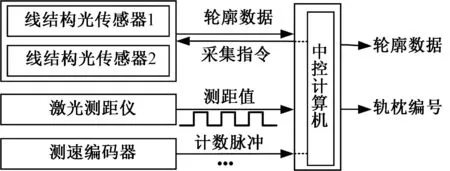
图4 传感器与中控计算机连接方式

中控计算机在检测时持续采集编码器发送的脉冲信号,当接收到的脉冲数达到设定的累计数量F时,中控计算机发送采集指令控制线结构光传感器完成一次采集。基于距离触发同步的方式能够确保采集到的轨道轮廓线间隔相等,不受推行速度变化的影响。编码器在转动过程中每旋转特定的角度会发出计数脉冲,设定线结构光传感器两次测量之间的目标间距S,可推算得到累计脉冲数量F,其关系式为

( 1 )

式中:r为载体小车的轮对半径;MPPR为编码器旋转一周输出的额定脉冲数;m为倍频数;F为设定的累计脉冲数;S为对应的移动距离。

线结构光传感器和激光测距仪之间的相对位置关系见图5(a)。测量的轮廓线GH和激光测距仪的测量中心O1共线,目的是确保设备在向前推行时两种测量传感器在推行方向上具有相同的位置基准。轨枕在轨道板上的间距固定且几何形状有明显的变化见图5(b),当激光测距仪以相对于轨道板表面固定的高度依次通过轨枕时,得到的测距值对应到轨枕的位置会有明显的突变。当测距值由大变小时,可以判定此时的检测系统开始进入轨枕测量区域。当测距值由小变大时,检测系统离开轨枕测量区域。通过不断累加轨枕编号的计数值,可以对检测系统通过的每一个轨枕进行标记并顺序编号。在此过程中,中控计算机会记录每一个轨枕编号对应的两个时间戳,后续可根据每一个轨枕编号对应的两个时间戳选取轨枕区域的轨道轮廓数据帧,从而建立二者之间的对应关系。

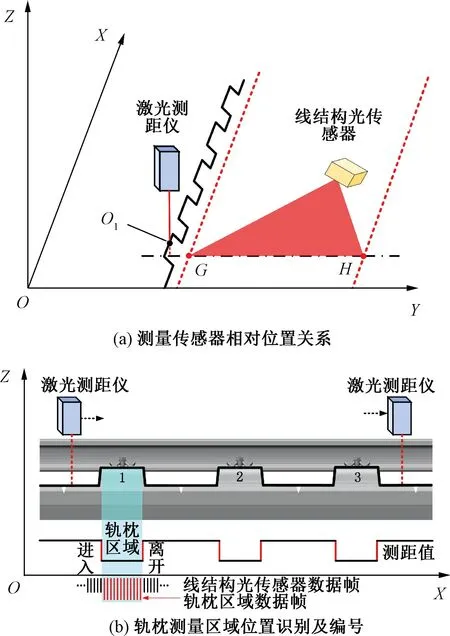
图5 轨道轮廓与轨枕位置对应关系说明

采用多传感器同步控制技术,确保了轨枕区域内轨道轮廓数据帧的选取不受编码器测量里程误差累积的影响,建立了轨道轮廓数据与轨枕位置的对应关系,为后续轨道结构高差特征值的提取和多周期数据之间的对比提供了准确的里程定位基准。

2 轨道结构高差特征值的计算方法

轨道结构高差特征值的具体计算流程见图6。首先,基于离缝检测原型系统,根据轨枕编号及时间戳信息提取每一个轨枕对应的轨道轮廓数据。其次,根据轨道的结构特点选取特定区域A、B和C内的轮廓数据用于后续空间直线的拟合。再次,采用RANSAC空间直线拟合的方法,对选定范围内的每一条轨道轮廓数据单独进行拟合,得到轨道结构表面的三段拟合直线。最后,计算每一条轨道轮廓线上,3条拟合直线之间在竖直方向上交点的距离,可得到一组对应当前轨枕编号的结构高差值。对测量数据中可能存在的异常值,通过设置结构高差阈值进行剔除,并在剩余数据中选取中位数作为当前轨枕编号对应的唯一轨道结构高差特征值。

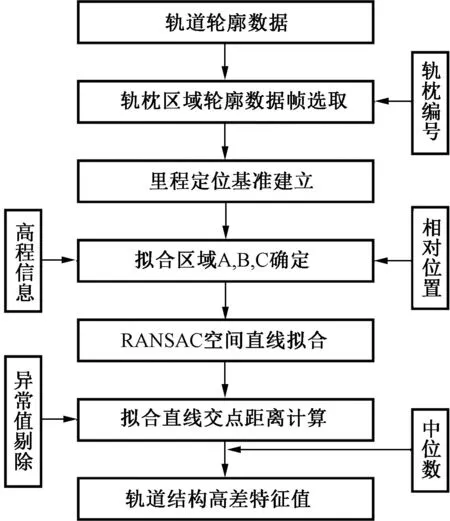
图6 计算流程

轨道轮廓数据见图7。由图7(a)可知,线结构光传感器以固定的间距获取轨道表面的轮廓,除部分区域受障碍物遮挡外,可以完整地采集轨道结构表面的三维轮廓数据。由图7(b)可知,选取A、B和C共3个区域内的轮廓数据用于空间直线拟合。3个区域划分的具体方法如下:

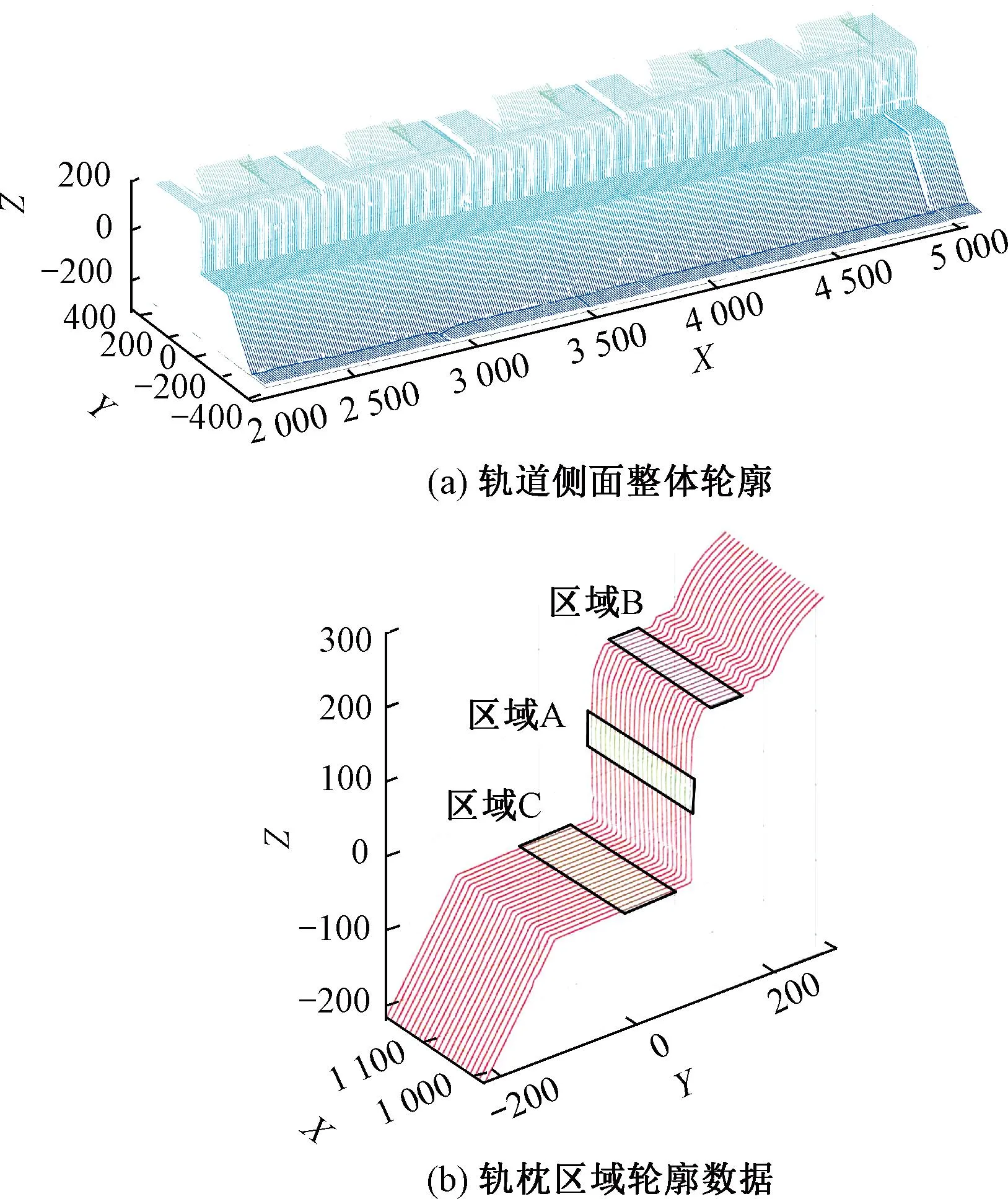
图7 轨道轮廓数据

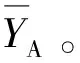
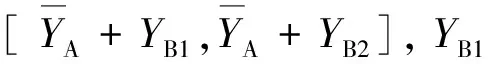
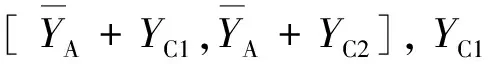
各参数的取值依据测量轨道板型的不同进行调整,以CRTSⅡ型板式无砟轨道为例,Z1、Z2分别设置为80、120 mm,YB1、YB2分别设置为30、70 mm,YC1、YC2分别设置为30、90 mm。

空间直线拟合法以最小二乘法和RANSAC算法[20]应用最为广泛,前者可以充分利用测量数据,但容易受到粗差点的影响。现实中的轨道板和支承层表面并不平整,因此测量数据存在大量噪声,使用最小二乘法难以拟合出正确的直线。因此本文采用鲁棒性更强的RANSAC算法,其核心思想为假设和检验,首先从数据集中不断随机选取部分数据,假设该部分数据均为内点并计算模型参数,然后通过数据集中的其它点对估计的模型参数进行检验,通过设定的最大阈值判断各数据点为“内点”或“外点”。经过一定次数的迭代,得到包含“内点”数量最多的模型,具体实现步骤如下:

Step1在测量数据中随机选取N个点作为“内点”,建立空间直线模型。

Step2计算采样余集到空间直线的距离。

Step3根据设置的阈值T区分其余点是否为“内点”,计算“内点数量”。

Step4选择“内点”个数最多的集合重新计算模型参数。

Step5通过计算所有“内点”与新计算模型的偏差评估模型。

RANSAC算法在计算过程中需要设置采样子集N,最大迭代次数K,距离阈值T,拟合较好时需要的最小样本点数量为Jmin。其中,三维空间直线拟合至少需要两个空间点,即N取2;距离阈值T设置为0.2 mm;Jmin设置为0,确保每次迭代都能收敛。迭代的终止条件可表示为

( 2 )

式中:s为“内点”在数据中的占比,设置最不理想条件下的初始值,然后随迭代不断更新;P为置信度条件,取值范围一般为[95%,99%]。本文设置初始值s为30%,P为98%。

结构高差特征值计算及拟合结果见图8。由图8(a)可知,对选定区域A、B和C内的每条轮廓数据使用RANSAC算法进行直线拟合,拟合后的3条直线相交于两点e和h,两点之间的欧氏距离即为轨道结构高差值d1。根据实测数据得到的拟合结果,结果保留两个交点及之间的拟合直线见图8(b)。由图8(c)可知,部分轨道板侧面的预应力钢筋可能会导致轮廓数据采集不完整,使得拟合后的直线出现异常角度。因此,为了消除这种异常情况对测量结果的影响,根据CRTSⅡ型板的结构尺寸,设置结构高差阈值d2的范围为[225,235]mm,对该组中的每一个高差值d1遍历筛选,剔除阈值范围外的异常值。最后,计算剩余高差值数据的中位数,将其作为当前轨枕编号对应的轨道结构高差特征值d。

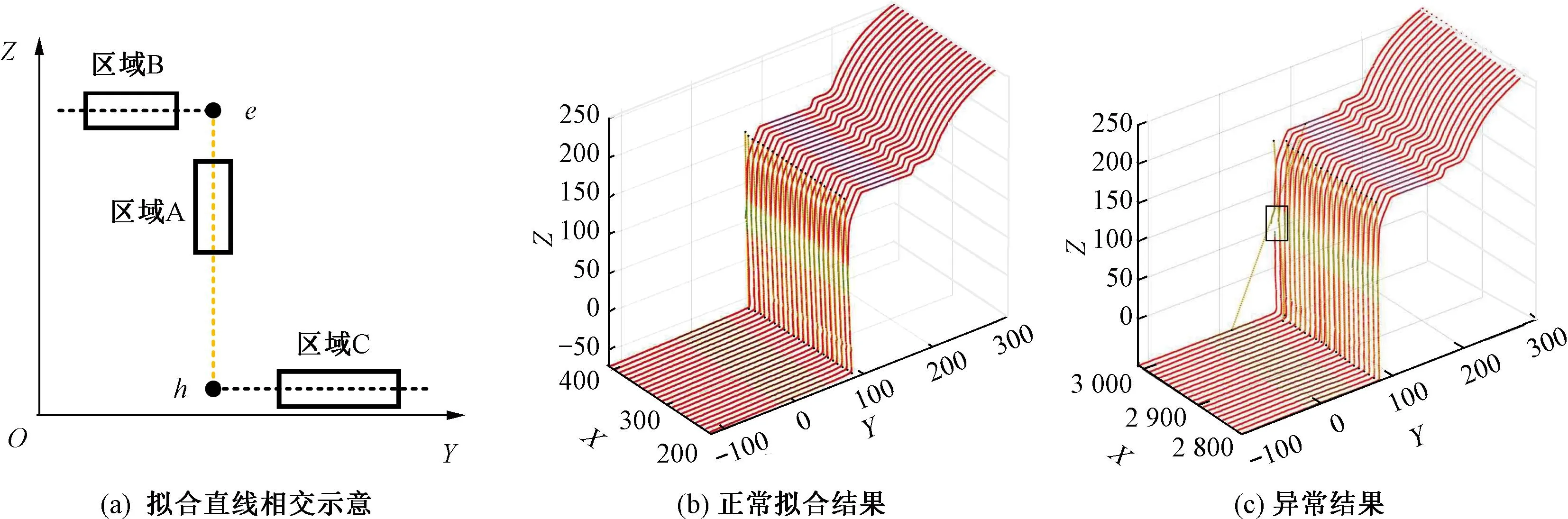
图8 结构高差特征值计算及拟合结果

本文在计算轨道结构高差特征值时,对轨枕区域内的每一条轨道轮廓线进行单独的拟合和计算,并未对整个选定区域内的所有轮廓数据进行总体的平面拟合。原因在于线结构光传感器在随检测小车运动时会不可避免的产生振动,这种振动对于计算单帧轨道轮廓数据,轨道板与支承层之间的相对高差值不会产生影响。因为线结构光传感器记录了被测物体与传感器之间的距离关系,而传感器自身姿态或位置的改变不会影响到被测物体内部的相互关系。如果联合多帧的轮廓数据进行平面拟合,此时拟合后计算的结果为两个结构面之间绝对位置的高度差,而振动产生的测量误差也会被引入到最终的测量结果中,降低最终的测量精度。

3 系统重复测量稳定性验证及测量偏差分析

检测原型系统的重复测量稳定性和测量偏差决定最终离缝定量检测精度。为评估系统的性能,高速铁路轨道测试场地进行多次重复测量试验,见图9。

图9 重复性测量试验

重复测量试验分为两次进行,第1次试验设置1#和2#结构光传感器分别在左轨和右轨的位置,沿图9中箭头标识的方向进行了3次重复测量。第2次试验交换两个传感器的位置,同样进行3次测量。试验中模拟系统正常检测时的运行速度为5～7 km/h。最终结果见图10。图10中,根据左轨和右轨测量位置的不同,将试验结果分为两组,每组包括6个对照组,对照组编号1、2和3对应1#线结构光传感器在左轨位置的3次测量结果,编号4、5和6对应2#线结构光传感器在左轨位置的3次测量结果。

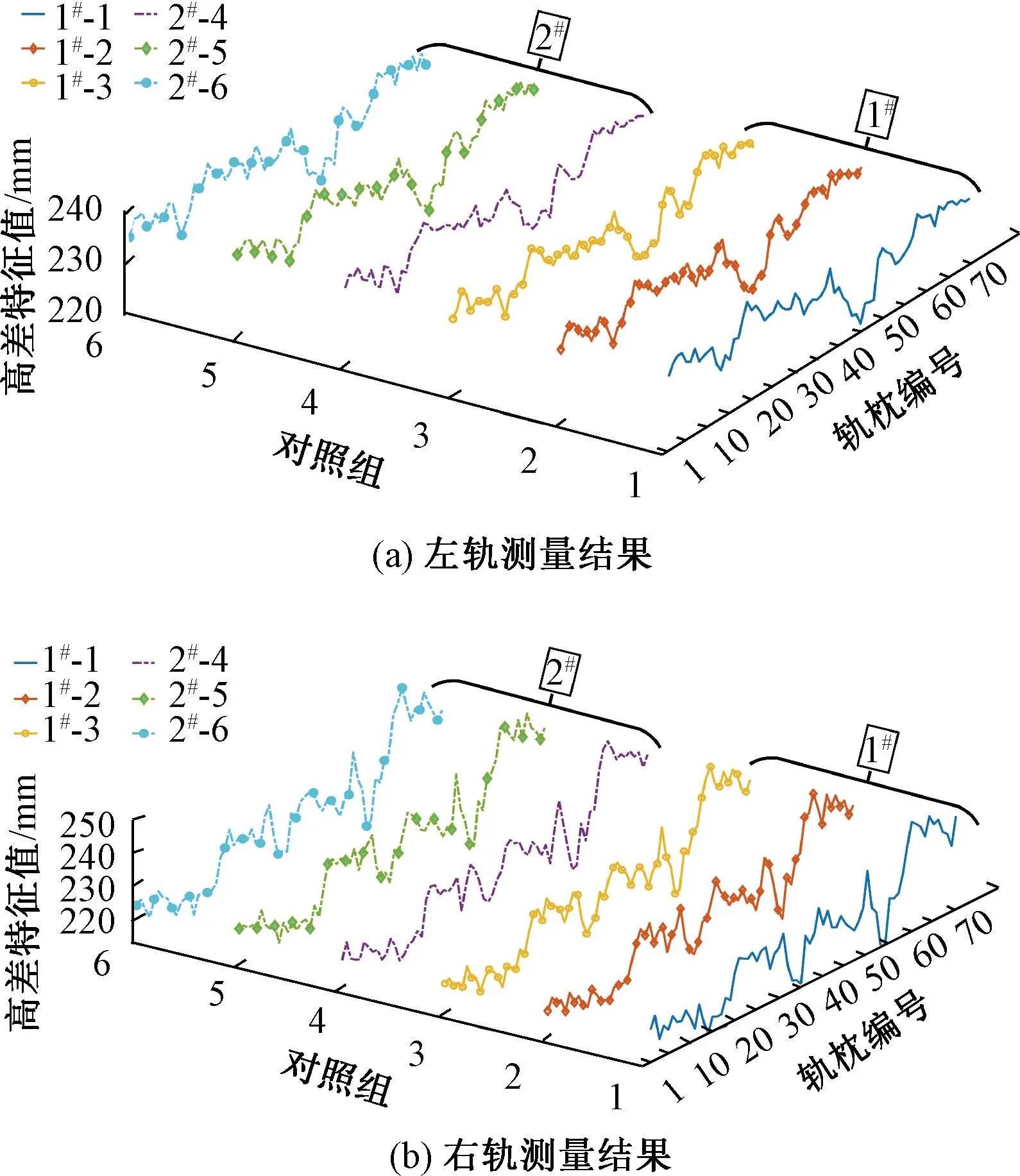
图10 测量结果

重复性测量结果对比见表1,计算了两次试验得到的12组数据的均值和标准偏差系数RSD,每组数据共计70个高差特征值。两个线结构光传感器在左右轨的测量结果都非常稳定。左轨测量结果的RSD介于0.015 2～0.017 3之间,右轨测量结果的RSD介于0.018 4～0.019 4之间,二者均保持稳定且小于2%。可见各组测量结果的重复性和一致性较好,离缝检测原型系统在重复测量时具有较高的测量稳定性。

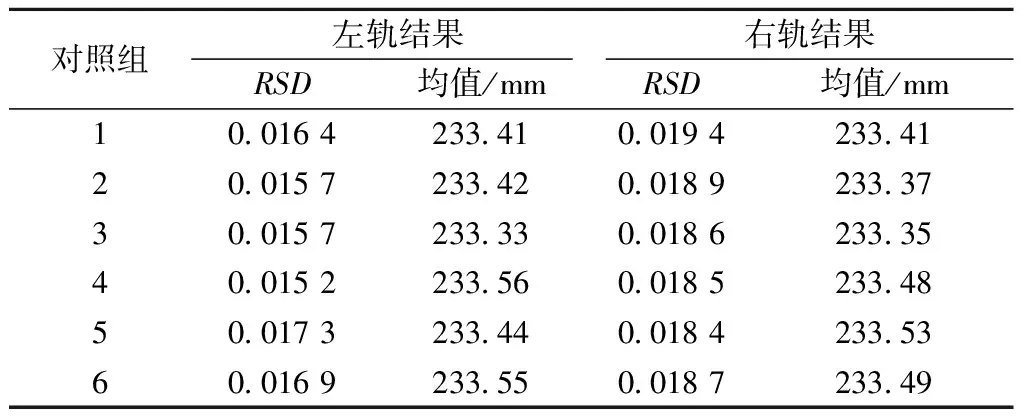
表1 重复性测量结果对比

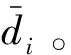
( 3 )

式中:dij为每个轨枕对应的高差特征值;j为对照组的编号;i为轨枕编号。

每个对照组中检测结果的测量偏差值Uij为

( 4 )

所有计算得到的测量偏差值的概率分布直方图见图11。由图11可知,分布范围为-0.41～0.44 mm,这表明重复测量的最大偏差始终能够保持在±0.5 mm的范围内。在置信度为95%的条件下求得测量偏差值的置信区间为[-0.25,0.25]mm,即试验结果总的测量偏差可以控制在±0.25 mm的范围内。一般情况下轨道板离缝的高度主要集中在0.5～3 mm的范围内。由于夏季高温导致的离缝高度普遍超过了1 mm。因此,本文构建的离缝检测系统能够满足实际线路离缝高度测量的精度需求。

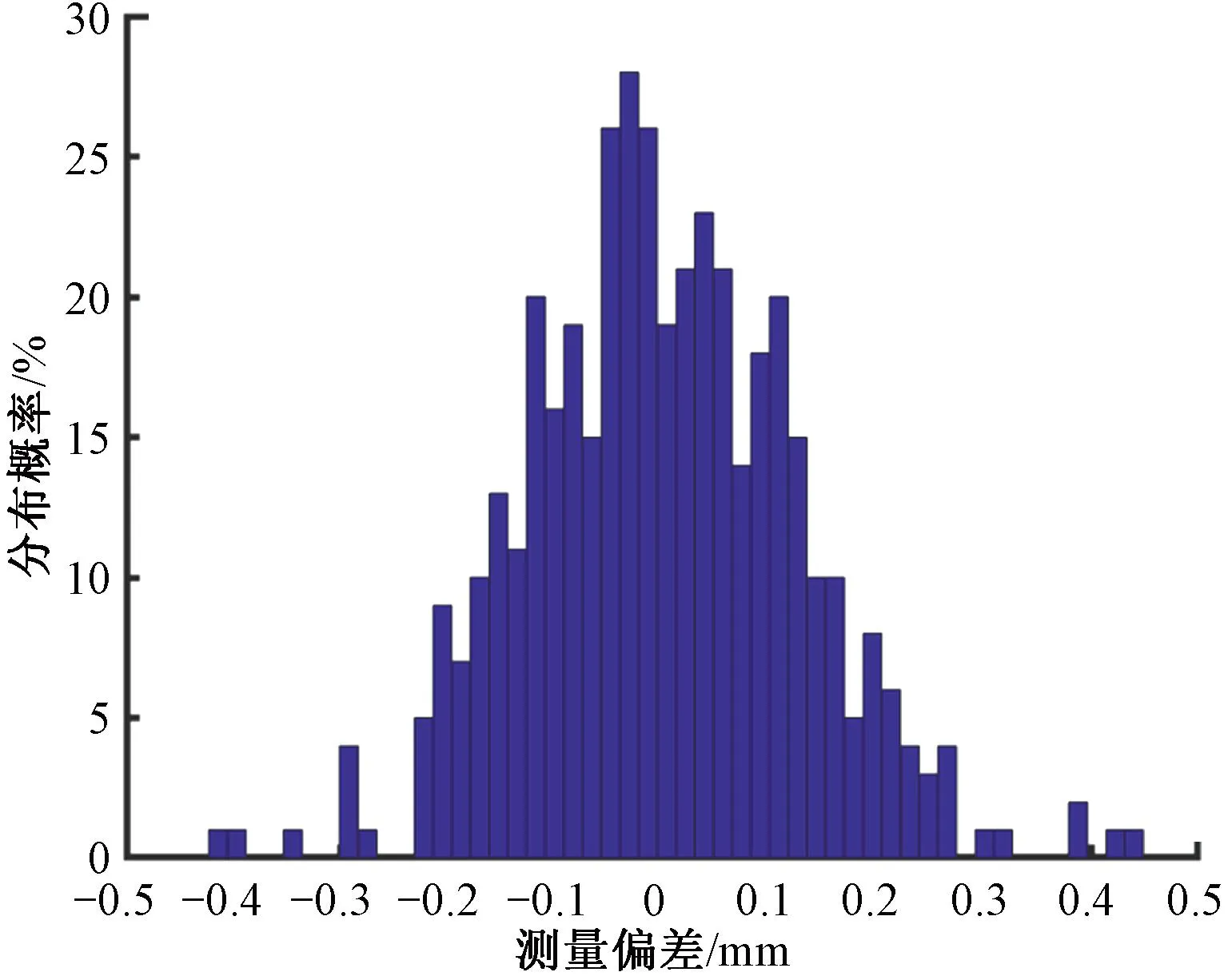
图11 概率分布直方图

4 离缝高度和长度的定量计算

通过对比不同的测量周期内,同一个轨枕编号下高差特征值的变化可以得到离缝的高度wi为

wi=d2i-d1i

( 5 )

式中:i为轨枕编号;d2i、d1i分别为同一轨枕编号对应的第2、1个周期的高差值。

离缝长度的计算主要根据离缝高度的变化判断其起始和终止的位置。根据重复性试验的分析结果,在未发生离缝病害的情况下,同一轨枕编号对应的两次测量结果之间的偏差会小于0.25 mm。因此,当对比结果wi>0.25 mm时,可以认定该轨枕编号对应的位置发生了离缝病害。选取了两组不同周期的CRTS Ⅱ型板式无砟轨道的测量数据进行对比,见图12。在图12(a)中,轨枕编号40550055～40550059的5个位置内,周期2的高差特征值明显增大,而且增幅均超过了测量偏差值。类似地,在图12(b)中,轨枕编号40517016、40517017这两个位置的周期2的高差特征值也明显增大,表现出与周期1相似的变化。

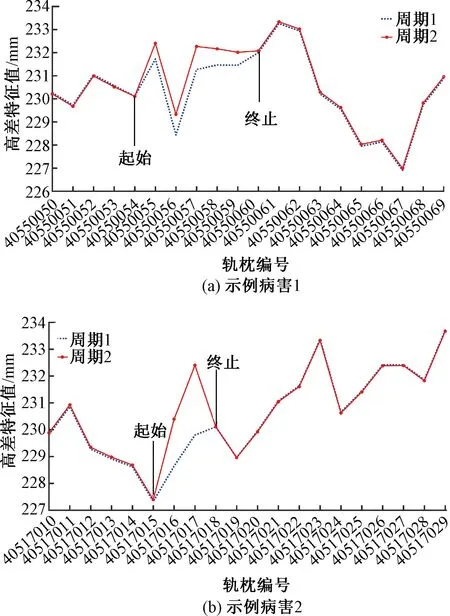
图12 两周期数据对比

以示例病害1为例,虽然有5个位置的离缝高度超过了测量偏差值,但离缝起始和终止位置的实际范围显然要更大。因为离缝的高度在起始和终止的位置是逐渐增大和减小的。所以确定示例病害1的起始位置位于40550054～40550055。同理,终止的位置位于40550059～40550060。这里,本文是以轨枕编号作为多周期数据对比的里程基准,因此示例病害1的起始位置统计为40550054,终止位置统计为40550060。由于CRTSⅡ型板式无砟轨道的轨枕之间的间隔为0.65 m,根据起始和终止轨枕编号之间的差值容易计算得到该处离缝的长度为3.9 m;同理,图12(b)中起始和终止位置的对应轨枕编号为40517015、40517018,对应离缝长度为1.95 m。

上述两个病害的高差特征值对比见表2。表2中,对应的轨枕编号只保留后3位。在离缝起始和终止范围内,离缝高度wi并不是定值,选择离缝高度的最大值作为此处病害的记录值。其中,病害1对应的054～060轨枕范围内,057号对应的差值最大为1.04 mm,则记录该值作为离缝的高度值。同理病害2对应的离缝高度为2.63 mm。

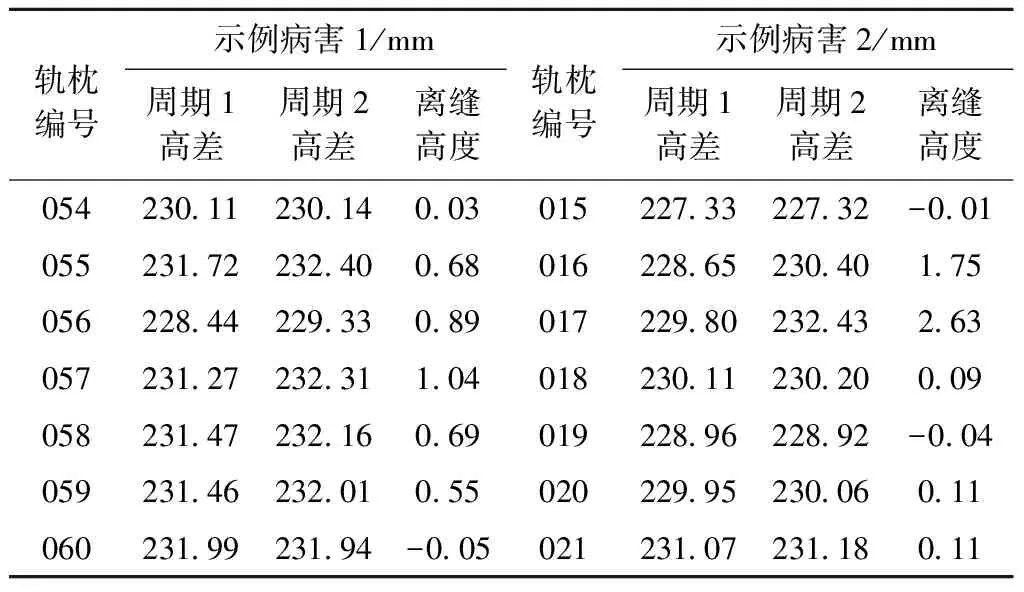
表2 离缝范围内高差值对比

5 试验验证

选取具有离缝病害的某CRTSⅡ型板式无砟轨道高速铁路正线进行试验,在相同的区间段内完成了两个周期的数据采集工作。两次检测间隔时间为1 a,检测时间均选择气温较高容易发生离缝病害的8月。为验证本文所提方法的有效性,将自检结果与铁路工务部门当期统计的病害库进行比对。对比结果见表3。表3中,对比的内容包括:自检离缝病害的里程范围和病害库中的对比里程,自检离缝高度w和离缝长度l,病害库中的对比值离缝高度w和离缝长度L。

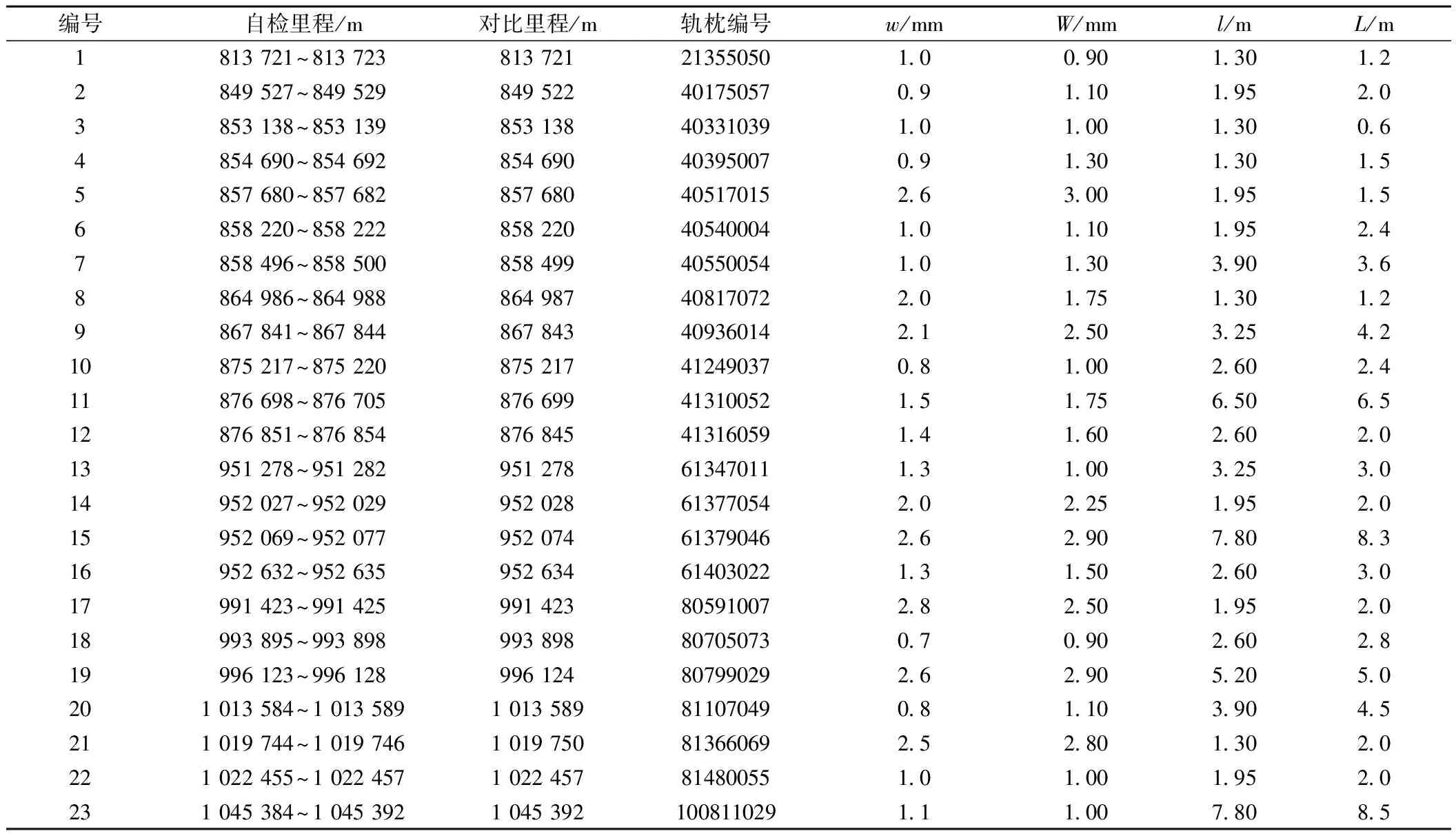
表3 试验结果

为离缝高度与长度的对比结果见图13。由图13可知,自检结果与病害库数据的吻合程度较高,这说明本文提出的离缝检测方法可以有效检测出轨道的层间离缝病害。以病害库中的统计结果作为对比标准,由式( 6 )和式( 7 )分别计算离缝高度和离缝长度检测结果的平均绝对误差MAE和均方对数误差MSLE。MAE用来衡量检测结果与对比结果的之间的实际差异,而MSLE则可以在评估检测结果误差时突出相对误差,降低个别异常值对结果的影响,提供一个更平衡的评估结果。

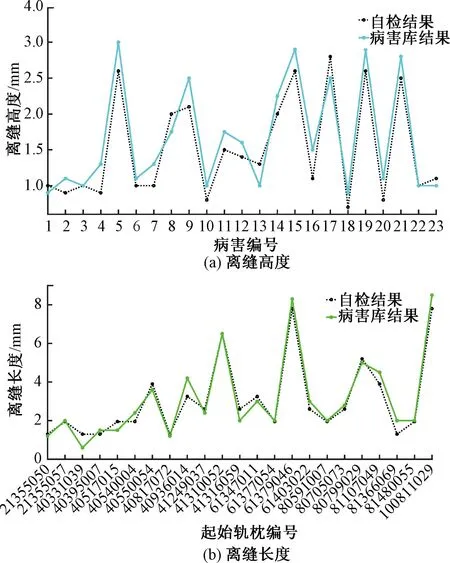
图13 检测结果对比

( 6 )

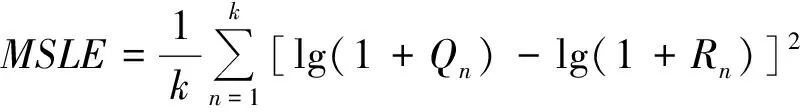
( 7 )

式中:n为病害编号;Qn为自检值;Rn为病害库中的对比值;k为总的样本个数,k=23。

离缝高度和长度检测结果的MAE分别为0.24、0.34 m,而MSLE分别为0.011、0.017。这表明本文的检测结果与病害库中统计结果的一致程度较高。其中,离缝高度的检测误差一方面源于检测系统本身的测量偏差。另一方面,离缝高度受温度变化的影响,不同测量周期内的环境温度也会导致离缝高度的变化。离缝长度的测量误差主要由离缝的起始和终止位置决定,由于本文以轨枕编号作为不同周期高差特征值对比的里程基准,所以最小的长度测量间隔为0.65 m。因此,当离缝病害的长度较短且起始和终止的位置距离轨枕相对较远,此时计算得到的离缝长度会出现一定误差。

对比病害库中离缝病害对应的里程信息发现,个别病害的里程信息不能完全对准。如表3中编号为2、12和21的病害,其里程定位的误差为5 m左右。虽然前后一块轨道板长度范围内的里程定位误差对于工务段的维护人员来说是可以接受的,但显然无法用于多周期高差数据之间的对比。通过修正算法或增加测量传感器的方法也很难彻底消除里程定位的误差。因此本文采用轨枕编号作为里程定位的基准,建立了与离缝信息之间的严格对应关系,有效避免了里程累计误差对离缝定量检测结果的影响。

6 结论

1)提出了一种基于轨道结构“轨道板-支承层”相对高差特征值的离缝检测方法,实现了无砟轨道层间离缝病害的定量检测。

2)研发了离缝病害检测原型系统,在速度为5～7 km/h的速度条件下,重复性试验测量结果的RSD值小于2%。在95%的置信度下,重复测量偏差的置信区间为[-0.25,0.25]mm,可有效区分离缝病害导致的异常值,实现离缝的快速检测。

3)采用轨枕编号作为对比基准,确保不同周期的测量数据能够严格对齐,进而实现离缝高度和长度的计算,解决了里程误差累计导致不同周期的测量数据无法精确对准的问题。

4)与病害库统计结果的比对发现,离缝高度、长度检测结果的MAE分别为0.24、0.34 m,MSLE分别为0.011、0.017。

5)研究成果能够显著提升离缝定量检测的自动化水平和效率,进一步促进了轨道安全运维技术的发展。