基于分形原理的岔区板式无砟轨道受力特性与伤损等级划分

向 芬,孙建营

(1.中铁二院工程集团有限责任公司,四川成都 610000；2.四川交投建设工程股份有限公司,四川成都 610000)

道岔作为线路的重要组成部分，实现了不同线路的交叉与连接[1]，道岔区的结构和受力复杂程度均与区间不同，属于轨道线路中的薄弱环节。通过现场调研发现，道岔区板式无砟轨道出现了较多的病害，其中层间离缝最为常见，实际的离缝区域多为不规则的形态，本文主要分析道岔区自密实混凝土底座板出现的层间离缝，运用分形几何模拟自然状态下离缝形态，明确离缝的存在对道岔结构的受力特性，从动、静力学角度提出了脱空伤损的维修限值，为后续检测和修复提供标准。

1 板式无砟道岔伤损分析

板式无砟道岔板采用预制板，底座采用流动性好，无需振捣的自密实混凝土现场浇筑，自密实混凝土底座现场施工质量的好坏直接影响道岔的质量，施工不当容易形成伤损[2]。离缝是指在结构层间由于材料和运营过程中各种外界因素共同耦合作用下，轨道结构不同部件之间出现的不可闭合的微小缝隙[3]，图1为道岔板与底座间离缝，底座与找平层离缝情况如图2所示。

图1 道岔板与底座层间离缝

图2 底座与找平层间离缝

2 利用分形原理模拟不规则离缝边界

2.1 分形原理

分形理论运用分数维度的视角和方法描述客观事物，分形研究的对象为不规则几何形态[4]，分形理论中维度可以为分数，典型的分形模型主要有Koch曲线，其维度为1.26(图3)。

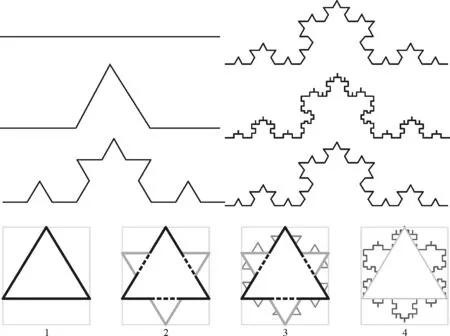
图3 Koch曲线

2.2 离缝边界模拟

离缝产生原因主要是温度梯度产生的翘曲和底座浇筑不密实。温度梯度产生的板角向上翘曲，离缝产生的形态主要呈弧形，现场单边注浆模拟试验可以得到类似的边界，可以看出液体扩散规律为半圆弧形向外扩散，且板角位置在灌注的时候不容易灌满，在现场施工中，判断注浆的终止条件为板边有浆液渗出，但实际道岔板下浇筑的密实情况仍难以直观判定，板的边缘位置容易出现离缝，不规则离缝的模拟示意图(图4)。

图4 注浆试验模拟

模拟不规则离缝边界可以借助分形的几何模型。通过对浇筑边界进行描摹得到一个不闭合曲线(图4中边界黑色边界线)，通过matlab计算得到该曲线的维度为1.397±0.169。在静力学计算中离缝区域的分形维度设置为1.26，目的在于运用经典的Koch曲线，构造不规则离缝边界的分形模型。

本文主要研究三种常见的不同型式的离缝(图5)。

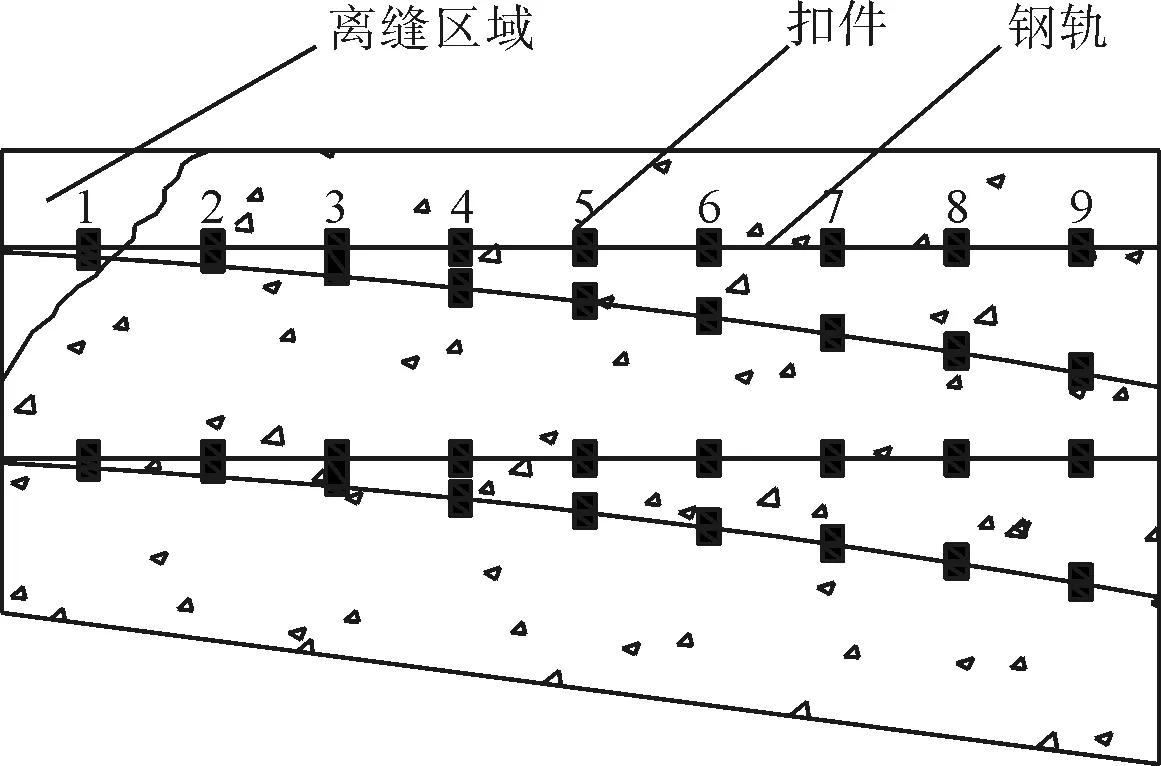
(a)板角离缝

(b)板端通宽离缝

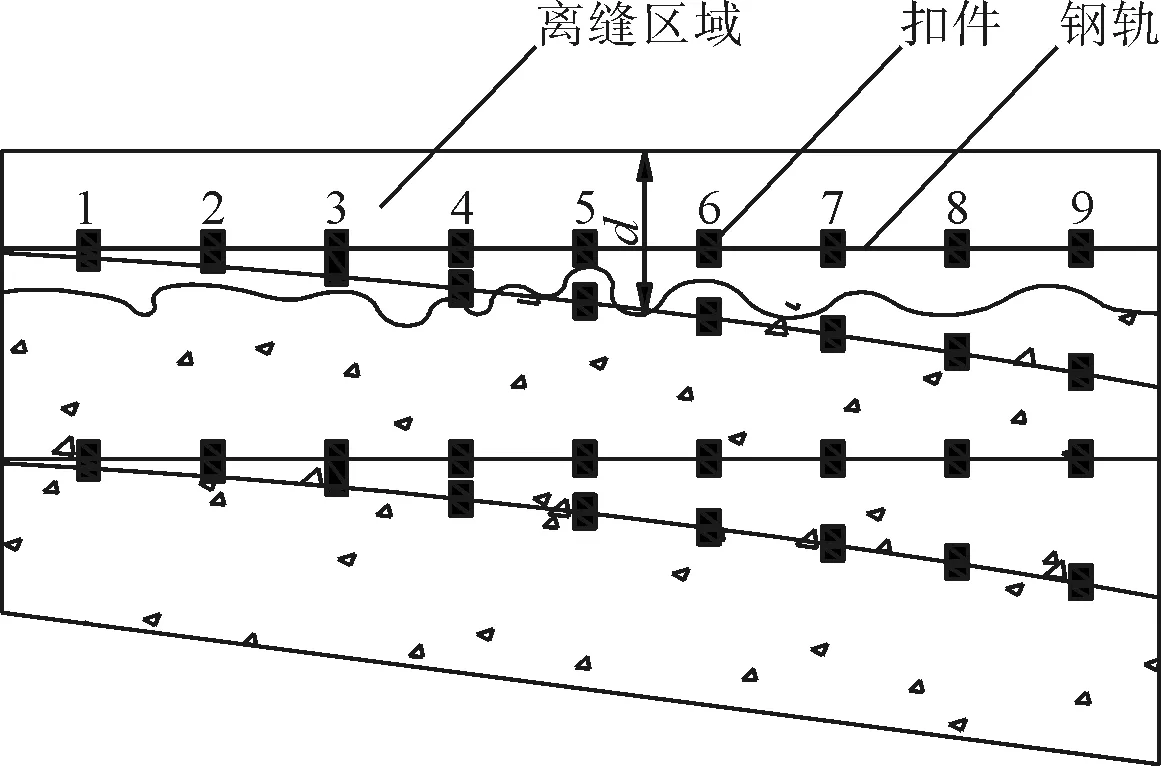
(c)板边通长离缝图5 不同位置道岔板底离缝示意

板端离缝长度由l确定，l为距板端最远距离；板边离缝长度由距离板边最远距离d确定；板角离缝由离缝面积A确定。伤损特性分析主要分析板式无砟道岔三个代表性区域：转辙区、导曲线区、辙叉区三个区域进行分析。

3 静力学分析

3.1 静力学模型与荷载取值

利用ANSYS建立有限元模型，模型如图6所示，脱空位置设置于道岔结构中受力比较复杂的心轨所在道岔板进行离缝脱空的影响分析[5]。主要考虑对无砟轨道影响较大的温度荷载和列车荷载，按参考文献[6]、[7]取值。

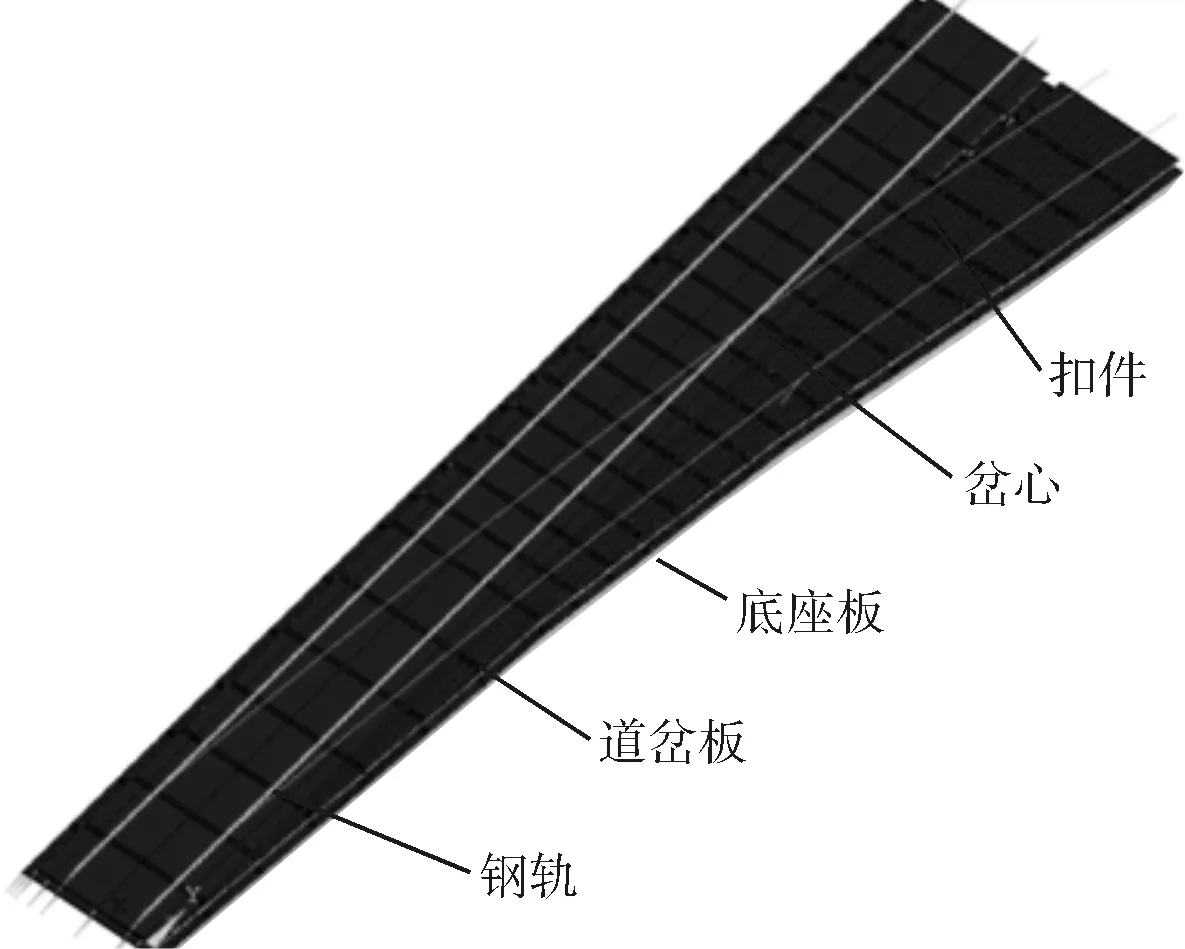
图6 有限元模型

3.2 离缝对道岔结构的影响

3.2.1 板角离缝对轨道结构的影响

道岔板在温度梯度与列车荷载作用时，板角位置的上下位移较大，从而易产生脱空。分析表明，板角脱空状态时，当列车荷载作用于板端第一个扣件处时，道岔板的受力状态最为不利，因此选择该荷载位置分析温度梯度和列车荷载共同作用下道岔区无砟轨道结构的受力情况(图7、图8)。

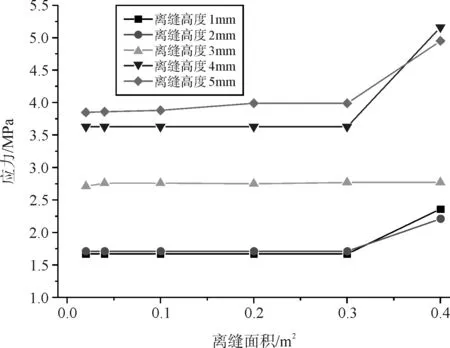
图7 道岔板纵向拉应力

图8 道岔板横向拉应力

当离缝达到轨下后应力和位移均有较大增加，C55道岔板混凝土开裂应力计算得[σcr]为 3.16 MPa，当离缝面积小于0.3 m2且离缝高度不超过2 mm时，道岔板纵、横向拉应力值小于混凝土开裂应力，当离缝高度超过2 mm时，混凝土表面开始产生横向裂缝。

3.2.2 板中离缝对轨道结构的影响

图9所示，随着离缝高度逐渐增加，在荷载作用下道岔板难与底座板接触，应力也缓慢增加，最大横向拉应力为2.89 MPa。

图9 离缝面积为0.1m2，辙叉区不同离缝高度道岔板应力

3.2.3 板端通宽离缝对轨道结构的影响

辙叉区道岔板不仅受到列车直向过岔的荷载作用，还受到列车曲向过岔的作用，随着离缝高度与板端离缝长度的不断增加，钢轨和道岔板垂向位移均随之增加，道岔板垂向位移变化更快。道岔板纵向拉应力在板端离缝长度小于0.4 m时增加较为缓慢，当离缝长度超过0.4 m时，拉应力显著增加，且离缝高度越大，增加速度越快。道岔板横向拉应力变化幅度相对较小。当板端离缝长度达到1.2 m时，道岔板纵向最大拉应力达到10.18 MPa，为正常无离缝时的3.01倍(图10、图11)。

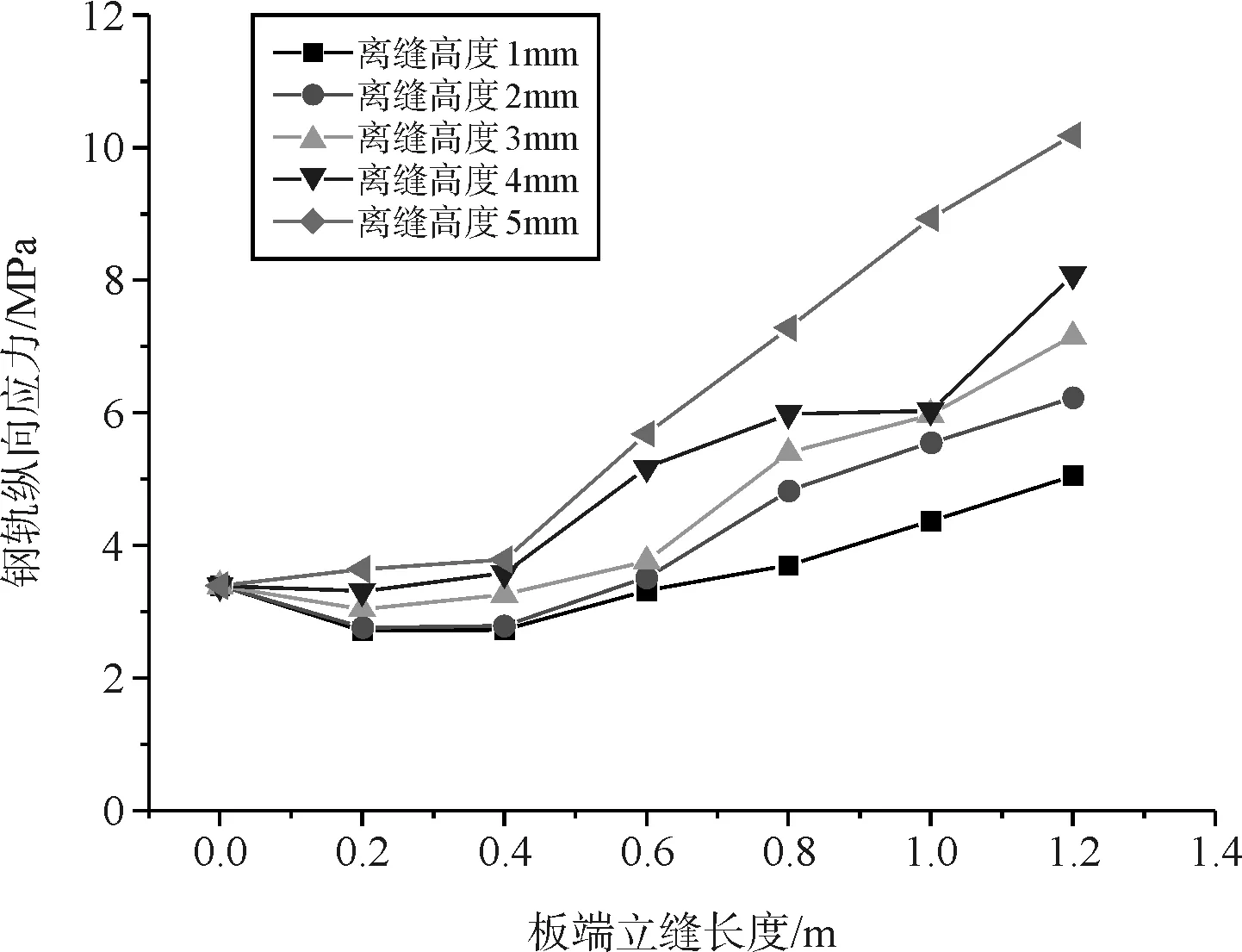
图10 道岔板纵向拉应力

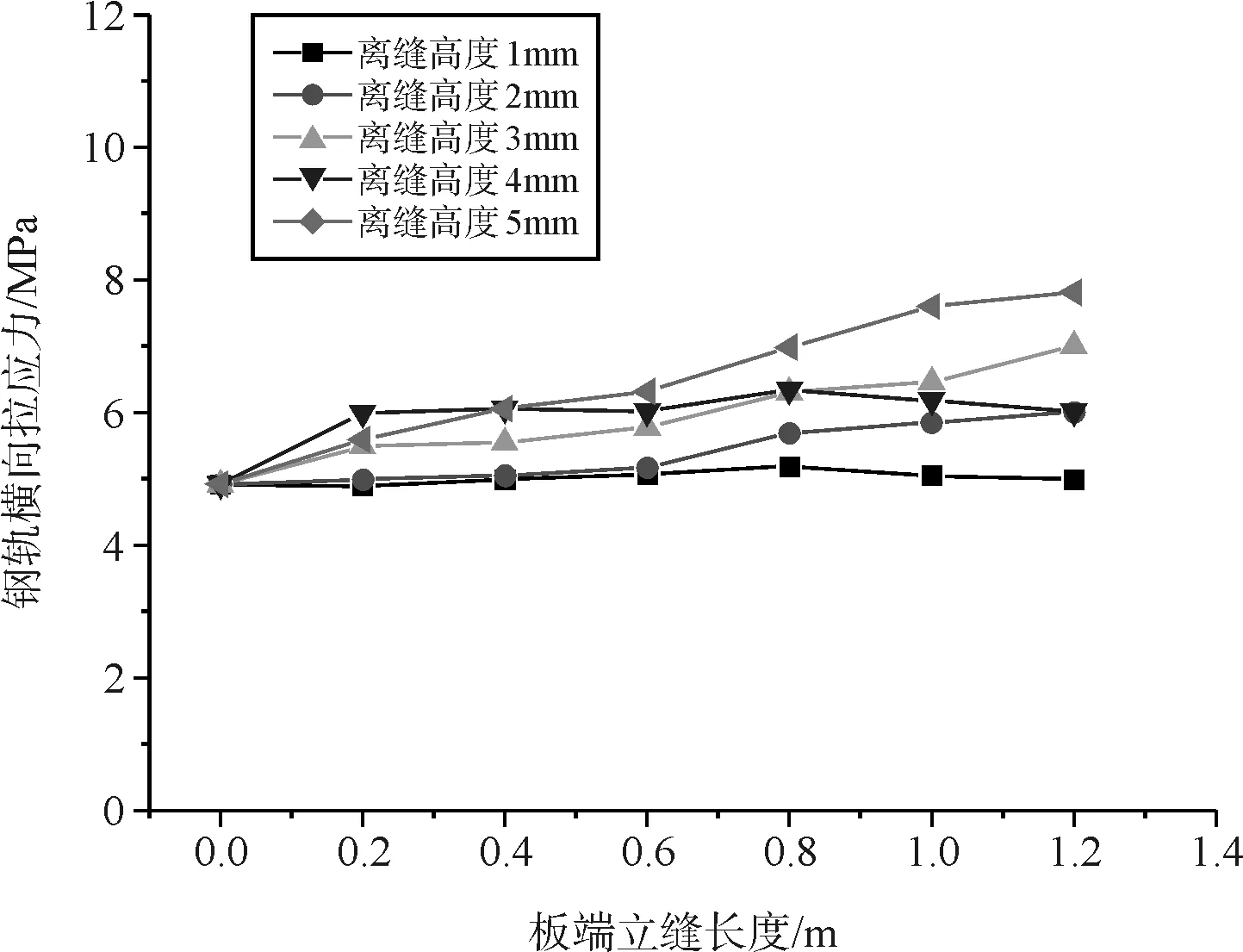
图11 道岔板横向拉应力

4 动力学分析

4.1 动力学模型

运用ANSYSY/LS-DYNA建立板式无砟道岔车辆-轨道垂向振动模型，模型如图12所示。道岔区轨道激励采用武广高速铁路不平顺谱[8]。动力响应评价指标参考文献[9]、[10]。

图12 车辆-轨道-下部基础有限元模型

4.2 离缝对轮轨系统动力性能的影响

4.2.1 板角离缝状态轨道动力响应

如图13、图14所示，由于底座板刚度大，较小的离缝面积对道岔整体结构影响较小，轨道结构动力响应变化率可以忽略，主要起主导作用的是钢轨自身不平顺。当离缝延伸至轨下后，轮轨垂向力与垂向加速度有明显的增加，最大轮轨拉应力为121 kN，并未超过最大轮轨力170 kN,。

图13 轮对垂向加速度

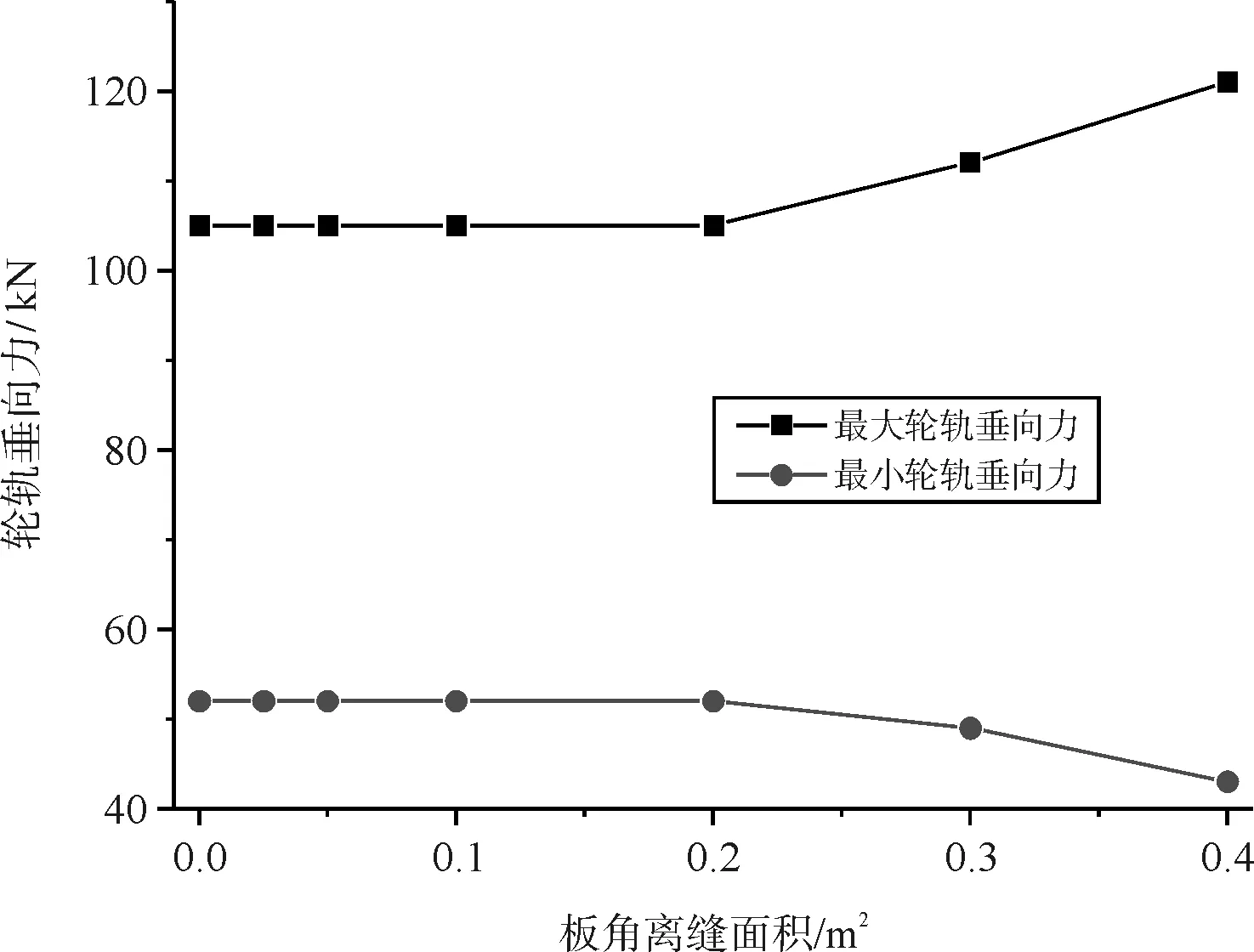
图14 轮轨垂向力

4.2.2 板端通宽离缝状态轨道动力响应

图15和图16分别为动车组第5节车辆后转向架后轮通过转辙区尖轨位置所在道岔板时，轮对加速度，离缝长度的变化关系。可以看出，离缝长度超过0.6 m时，轮对加速度和轮轨垂向力最大值随离缝长度的增大明显，轮轨垂向力最小值随离缝长度减小明显。板端横向离缝长度为1.0 m时，离缝超过第二组扣件后，轮对加速度为4.09g，较正常状态增加了36.4 %，最大轮轨垂向力仍小于170 kN。

图15 板端离缝轮对垂向加速度

图16 板端离缝轮轨垂向力

4.2.3 板端通宽离缝状态轨道动力响应

图17、图18分别为动车组第5节车辆后转向架后轮通过转辙区尖轨位置所在道岔板时，轮对加速度、最大和最小轮轨垂向力随离缝长度的变化关系。板边离缝长度不超过0.6 m时，轮对加速度和轮轨垂向力变化较小，离缝长度超过0.6 m时，即当离缝超过轨下时，轮对加速度和轮轨垂向力最大值随离缝长度的增大明显，轮轨垂向力最小值随离缝长度减小明显。板边横向离缝长度1.0 m时，轮对加速度为4.16g。

5 道岔板与底座离缝维修限值的制定

明确道岔部件的伤损维修级别是进行修补的主要依据，在保证行车安全性与平稳性的前提下，减少维修工作量并延长道岔部件的适用寿命。通过参考国内外运营实践，将伤损等级划分为I级、II级和III级。对Ⅰ级伤损应做好记录，对Ⅱ级伤损应列入维修计划并适时进行修补，对Ⅲ级伤损应及时修补。根据不同离缝形式与特征，结合前述计算结果，提出了维修限制建议值，见表1。

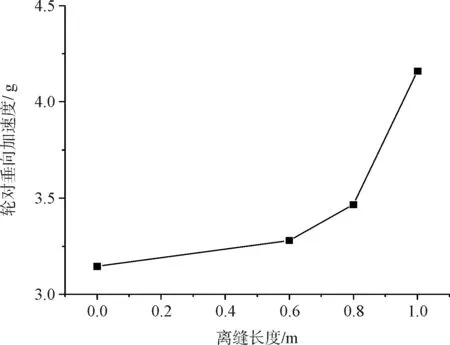
图17 板边离缝轮对垂向加速度

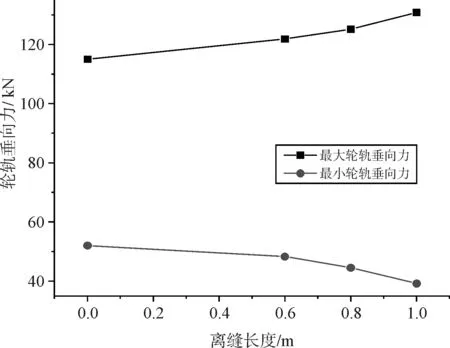
图18 板边离缝轮轨垂向力

6 结论

本文利用有限元分析软件，针对板式无砟道岔建立有限元模型进行理论分析，对道岔板不同形式的离缝，分析了静力荷载作用下道岔结构受力与动力荷载作用下道岔结构动力响应，并得出了道岔板在不同形式的离缝作用下受力规律，并提出了关于道岔板层间伤损维修等级划分。得出了以下结论：

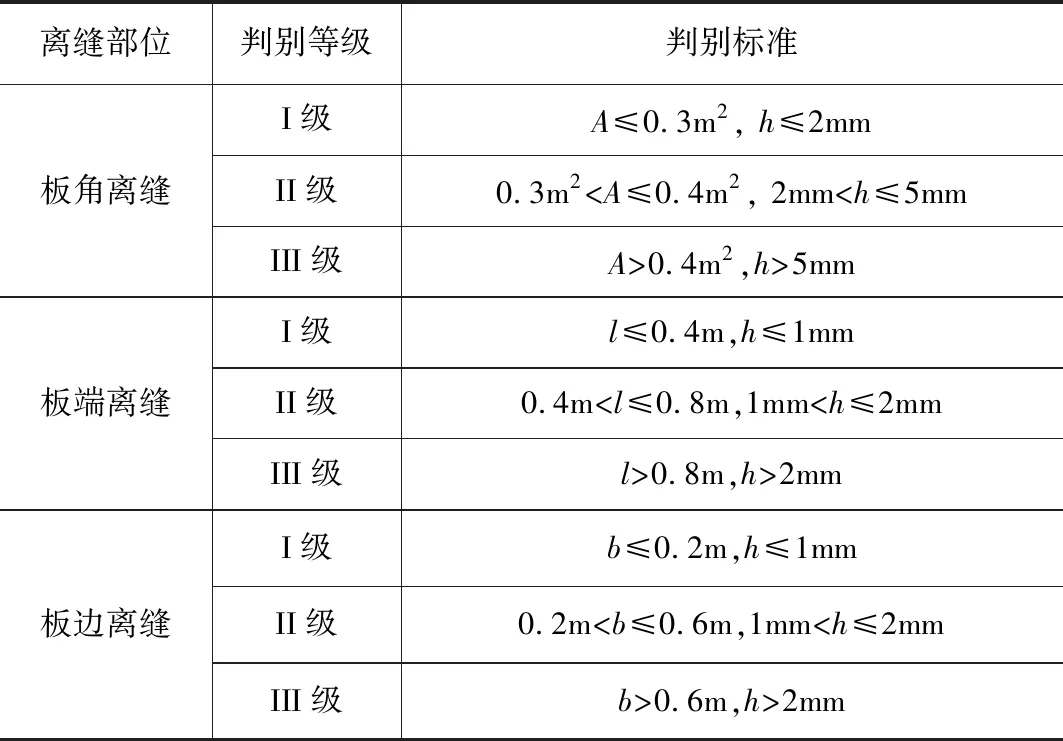
表1 板角离缝伤损限值建议值

(1)在静力学分析中表明，板角离缝存在时，当离缝面积超过0.3 m2，应力超过道岔板混凝土开裂应力。当板端离缝长度超过0.8 m、离缝高度大于2 mm时；当板边离缝长度超过0.6 m、离缝高度超过2 mm时，道岔板纵向拉应力达到正常状态的数倍并超过道岔板混凝土开裂应力，此时道岔板表面裂缝出现并不断发展成为贯通离缝。

(2)在动力学分析中表明，板角离缝对轨道结构影响较小，道岔结构动力响应主要是来源于钢轨自身不平顺。当板端离缝长度大于0.4～0.8 m时，轮对加速度、道岔结构相对位移有明显增加，由离缝产生的不平顺起主导作用。当板边离缝超过0.6 m，也就是离缝超过轨下，道岔系统动力响应急剧增加，影响道岔结构列车过岔的平顺性与安全性。

(3)结合预防性维修伤损特征，分别对板角离缝、板中离缝、板端离缝、板边离缝维修限值划分为I级、II级、III级三个等级，为维修提供一定的参考。