一种惯性式路基激振装置的研发与现场标定
崔颖辉,罗 强,冯桂帅,王腾飞
(1.中国国家铁路集团有限公司,北京 100844;2.西南交通大学 土木工程学院,四川 成都 610031;3.西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031)
路基是铁路线路工程重要基础设施之一,承受上部轨道结构荷载和列车运行产生的动力作用[1]。提升列车运行速度将大幅增加路基受荷频率[2],加剧路基短时动力响应与长期累积变形,带来疲劳破坏、过量沉降等长期服役问题,对线路运行品质产生影响[3]。
列车荷载作用下,轨道-路基系统动力响应特性和耐久性评估是铁路路基工程的关键问题之一[4]。理论模型[5]、数值仿真[6]等方法被广泛用于探究轨道-路基系统动力响应、路基在列车动荷载作用下的累积变形[7]等问题。同时,开展室内试验[8]、原位测试等工作为理论与数值模拟提供数据支持。原位试验一般有两种类型:实车条件下路基结构动力响应的现场监测和路基建设期模拟列车荷载作用的激振试验。通过开展原位试验,分析实测数据,有助于客观评价路基服役性能,为路基结构设计建造提供参考。
目前,已对水泥改良膨胀土路基[9]、石灰稳定风化红层泥岩路基[10]、高速铁路路基半刚性防水功能层[11]、硅藻土路堑防排水基床[12]、桩板结构[13]等开展了路基原位激振试验研究,大部分试验借助激振装置模拟列车动载及轨道自重。已有研究主要关注路基动力特性与工作特性,而对路基激振装置的设计研发关注较少。
为此,对激振设备和路基工程中已有的激振装置资料进行调研,选用双轴惯性式振动电机作为动力源,自主研制一种便携式路基激振装置ISV400,并对不同技术参数配置(供电频率、偏心片和配重块数量)下的输出荷载(激振频率、峰-谷值和谷值应力)进行标定,分析激振频率和激振力变化规律,最终提出满足现场动测需求的设备配置方法。研究成果有助于完善新型路基激振装置的研发。
1 路基激振设备调研分析
1.1 激振设备的分类及特点
激振器是一种对被测系统施加预定激振力,引起被测系统振动的机械设备,其按工作原理分类,常见的有惯性式、电磁式和液压式。
1) 惯性式激振器
惯性式激振器利用偏心块旋转产生的离心力提供激振力,见图1(a)。两只转轴平行布置且反向等速旋转的双轴式激振器,水平方向合力为零,竖向激振力Fv以简谐规律变化,即
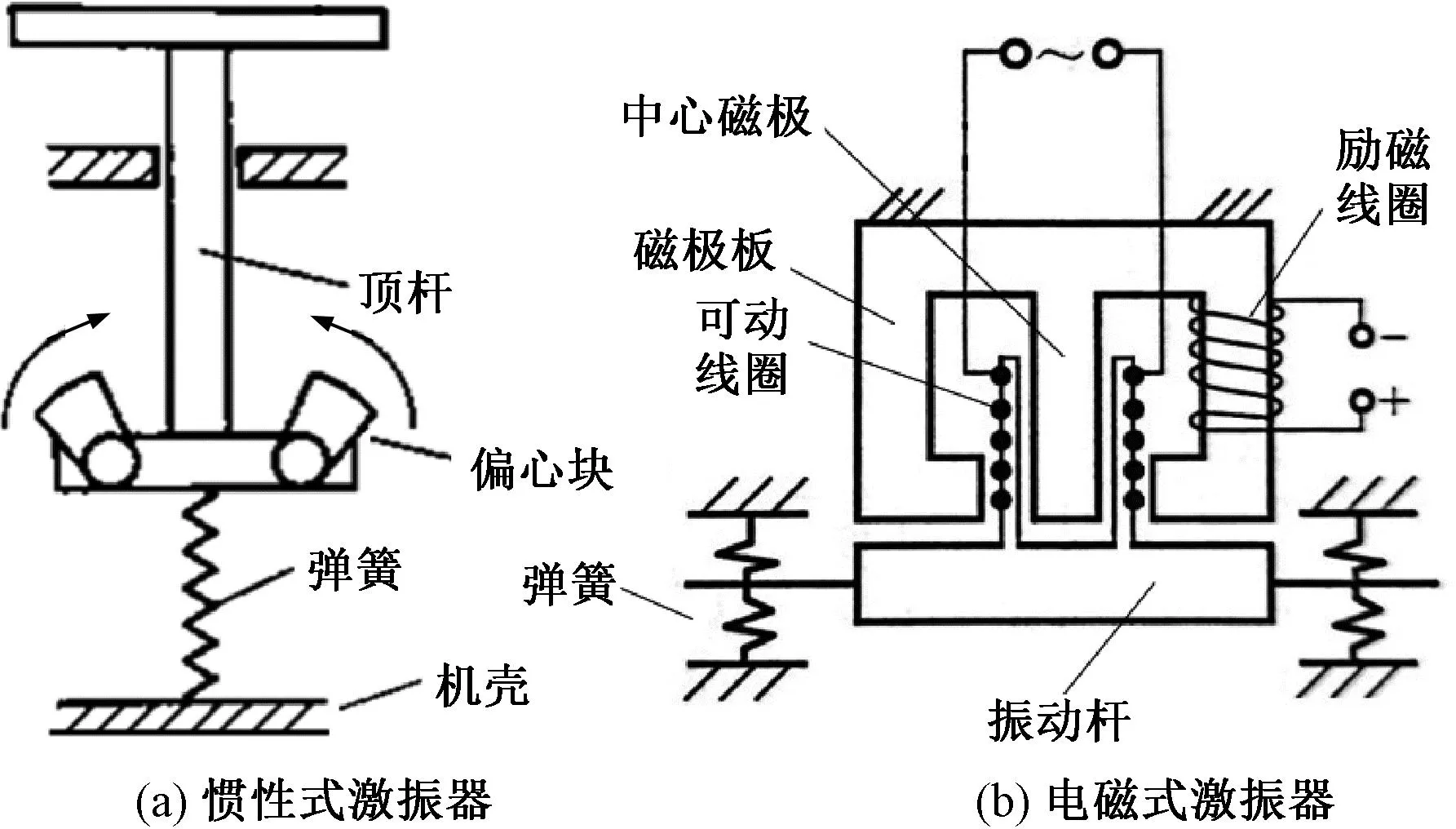
图1 惯性式和电磁式激振器结构简图[14,15]
Fv=mω12e1sinω1t
( 1 )
式中:m为偏心片质量;ω1为偏心块旋转角速度;e1为偏心块偏心距;t为偏心块旋转时间。
惯性式激振器结构简单、性能可靠且维修方便,应用较为广泛,但其荷载输出类型仅限简谐荷载,长期使用累积的机械磨损会导致信号失真。技术性能方面,激振力可达数百kN,频率一般不超过50 Hz。
2) 电磁式激振器
此类利用电磁感应原理产生振动,核心部件为励磁线圈和可动线圈,见图1(b)。直流电通入励磁线圈,中心磁极周边形成磁场,动圈通入交流电后受到电磁力Fem作用,驱动振动杆振动,Fem计算式为
Fem=BLImsinω2t
( 2 )
式中:B为磁感应强度;L为动圈有限长度;Im为交流电幅值;ω2为交流电圆频率。
电磁式激振器需搭配信号发生器、功率放大器组成激振系统,结构比惯性式激振器复杂,且采用电信号驱动,可输出简谐、脉冲、随机等多种荷载,激振力和频率的调节较便捷。技术性能方面,激振力一般仅为数kN,频率最高可达104Hz。
3) 液压式激振器
通过控制流体的压力、流向,液压式激振器可将高压油液的流动转换为活塞杆的直线往复运动。典型的液压激振系统包括驱动系统、油路系统和作动器等。其中,驱动系统由电动式驱动器搭配信号发生器和功率放大器组成,油路系统由功率阀、控制阀等多级控制设备调控。
液压式激振器结构复杂,故障类型多样,维修难度高,使用场景以室内居多;由于可采用闭环控制,易实现多台作动器同步运行或相位精确控制;内置电力驱动系统保证了激励信号的丰富性与输出调控的便捷性。技术性能方面,激振力一般可达数千kN,频率一般不超过10 Hz。
由于系统结构和工作原理存在差异,各型激振器工作性能也有差别,其常见类型的技术性能指标见表1。表1中,相关数值仅反映量级水平。

表1 各型激振设备技术性能指标
1.2 激振设备在路基工程中的应用
中国、日本、德国等国家开展过路基激振设备的研发及工程应用,无一例外均采用惯性激振方案,其设备技术参数见表2。表2中,PRIT、ZSS50的工作面为轨面,需待轨道结构铺设完毕后方可开展试验;其余设备工作面为路基面或路基结构层表面,DTS-1、SBZ60在试验前需根据模拟需求单独设计钢筋混凝土底座。

表2 路基原位激振现有设备的技术参数
2 激振装置结构设计及控制原理
开展路基原位激振试验,主要考察激振器的激振力和激振频率。基于铁路路基实际工况分析试验模拟需求,最大激振力按列车轴重15~20 t考虑;激振频率按车速350 km/h和车长25 m计算,其上限为4倍的过车频率[24],约15.6 Hz。在此量级上,电磁式激振器激振力较低,液压式激振器激振频率不足,惯性式激振器激振力和激振频率均大致满足试验需求,且其结构简单、维修方便,是路基原位激振设备研制的优选。基于设备性能和试验需求的综合考量,现有设备均采用惯性式激振器作为振动源。
现有路基激振设备为大型试验设备,体积和自重较大,难以在狭小或软弱场地开展试验,安装、调试及运输也并不便捷。因此,研发小体量路基原位激振装置,使试验操作简便,对提升运输效率、拓展设备工程应用场景和范围具有积极意义。
2.1 激振装置结构设计
路基原位激振装置ISV400由西南交通大学自主研制,主要由动力机构、荷重机构和防护机构组成,技术参数见表3。
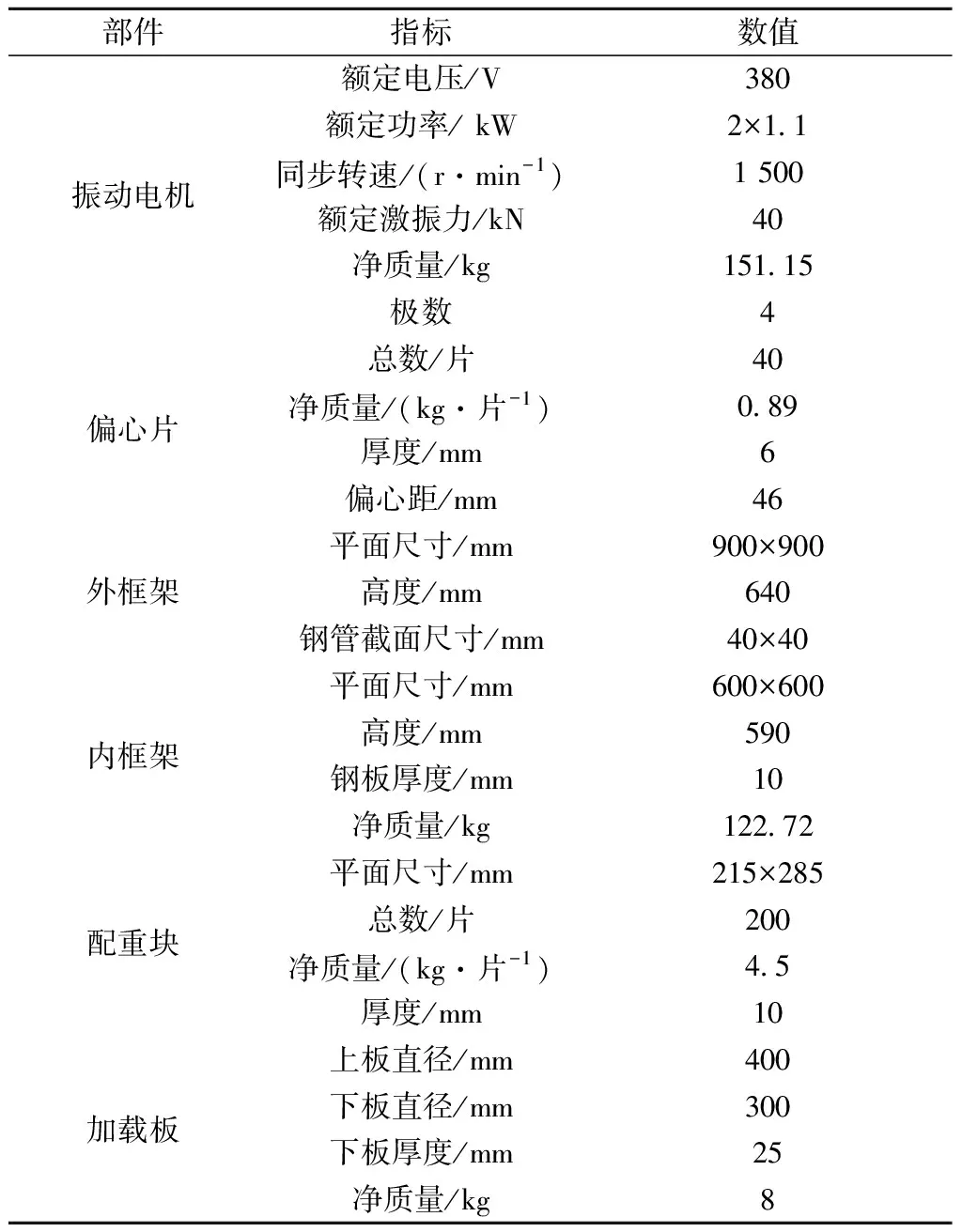
表3 ISV400技术参数
1) 动力机构由1台双轴式三相异步振动电机(ZWE-20)和变频器(A90-4T5R6B)组成,变频器可通过控制电机供电频率调节电机转速。电机2只转轴基于自同步原理[25]实现同步运行,转轴每端最多挂载10片偏心片,各端偏心片挂载数量保持一致。
2) 荷重机构位于动力机构下方,由上至下依次为内框架、配重块和加载板。内框架上下两端利用螺栓与电机和加载板固接,内部设有8个配重格室(上、下各2层,每层4个),每格室可安装25块配重。矩形配重块由10 mm厚钢板切割而成,调节设备配重按4块1组同时增减。加载板由上、下2块圆形钢板焊接而成,上板与内框架固定,下板作用于路基结构层表面。
3) 防护机构位于荷重机构外围,包括外框架、滑轮和沙袋。外框架通过地钉与路基结构层锚固,外侧堆沙袋防倾倒,滑轮与内框架预留一定缓冲间距。振动电机与荷重机构组合体是ISV400的可动部件,荷载经内框架传递由加载板施加给路基结构层。
DYSTAFIT、SBZ60和DTS-1等大型激振设备的工作面为路基面,且加载板面积较大,应力影响范围涵盖路基深度,测试对象为整体路基结构。区别于已有设备,ISV400加载板面积较小,主要用于浅表测试,测试对象为路基结构层,工作面为各结构层表面,不限于路基面。便携性以及对狭小、软弱场地的适应性是ISV400区别于已有设备的突出优势。
2.2 激振装置输出调控
ISV400激振力输出指标为加载板板底应力σ,理论的激振力典型波形曲线见图2。图2中,σs为静态荷载;σc为动态荷载幅值;σp为激振力峰值;σv为激振力谷值,σd为激振力峰-谷值。
σs源于ISV400可动部件的净重,其表达式为
σs=msg/S
( 3 )
式中:ms为包括电机和荷重机构在内的可动部件总质量,kg;g为重力加速度;S为加载板面积。
σc来自偏心片旋转产生的离心力,其幅值表达式为
σc=mcω2e
( 4 )
式中:mc为偏心质量,kg;ω为偏心片旋转角速度,rad/s;e为偏心距,m。
σs叠加σc后,可得激振力曲线的峰值σp和谷值σv,其表达式分别为
σp=σs+σc=msg/S+mcω2e
( 5 )
σv=σs-σc=msg/S-mcω2e
( 6 )
开展路基原位动测,σv模拟轨道及上覆路基结构层自重,σp与σv的差值σd(峰-谷值)模拟列车运行引起的路基动应力,其表达式为
σd=σp-σv=2σc=2mcω2e
( 7 )
电机激振频率fout与其实际转速n的关系为
fout=n/60
( 8 )
三相异步电机实际转速n略低于同步转速n0,其关系为
n=n0(1-s)
( 9 )
n0=60fin/p
(10)
式中:s为转差率,取值范围一般为1%~6%;fin为经变频器调频后输入电机的供电频率,Hz;p为电机极对数量,数值上为极数的1/2。
我国国家标准的电网频率为50 Hz,将电网交流电通入变频器后供给振动电机,即可通过变频器调节电机供电频率fin,实现电机的无级调速。变频器调频实行下调模式,则由式 ( 8 )~式 (10)可知,四极电机fout可调区间为0~25 Hz。
由式( 7 )可知,σd与σc有关。激振装置可通过mc或ω调控σd,实现手段分别对应增减偏心片数量Nc和调节电机实际转速n,满足式 (11)、式 (12),而n则需由变频器调节fin实现。
mc=Ncmc0
(11)
ω=πn/30
(12)
式中:m0为单只偏心片质量,kg。
式( 6 )表明,σv与σs和σc均有关,除控制Nc和fin外,还可通过增减配重块数量Na调节可动部件总质量ms进行调控。
ms=me+mc+Nama0
(13)
式中:me为可动部件除偏心片和配重块外的总质量,kg;ma0为单块配重质量,kg。
综上,激振频率fout、峰-谷值应力σd和谷值应力σv同时受电机供电频率fin调控,改变Nc同时影响σd、σv,Na独立调节σv。
3 标定试验方案
3.1 测试设备
标定试验场地位于某高速铁路路基施工现场,激振装置工作面以下为整体性良好的弱风化红层泥岩路堑。测试设备包括德国imc数据采集仪、计算机、荷重传感器及标定板,见图3。数据采集仪实时采集信号并传输到计算机并进行存储,可处理信号频率最高为105Hz,现场测试的采样频率为103Hz。标定板介于加载板和路堑面之间,由上、下板组成,两板直径均为300 mm,厚度10 mm。3支QLMH-P型荷重传感器安装于两板之间,空间上互成120°分布。传感器量程2 t,精度6 kg,分辨率2 kg,灵敏度2 mV/V。激振力通过标定板和传感器组合体进行测试,相对于传感器测试值的转换系数为0.139 kPa/kg。
3.2 测试方法
测试工况见表4。针对Na、Nc的组合,开展fin为0~50 Hz的扫频试验,对激振装置激振力进行标定,分析输出量(fout、σd、σv)与控制参数(fin、Na、Nc)的关系,确定激振力估算方程,建立面向路基现场动测试验的激振设备配置方法。

表4 测试工况
4 标定数据分析
4.1 测试波形及激振频率
以工况Na=200片、Nc=4片为例,部分激振力测试波形见图4。图4中,测值为负表示荷载方向竖直向下。

图4 实测信号
由图4可知,当fin<10 Hz时,波形欠光滑且不规整,激振装置动态输出稳定性差。由于采用自同步技术,电机低速运行时两轴间存在相位差,水平荷载分量导致设备运行状态欠佳。当fin>10 Hz时,电机转速提高,两转轴同步性较好,曲线波形规整、峰谷值稳定,设备工作状态良好。
对实测信号作快速傅里叶变换(FFT),可获取fout与fin关系曲线,见图5。由图5可知,二者线性关系良好,测试结果并未体现s的作用。误差允许范围内,fout可按fin的1/2计算,则激振装置工作频率区间为5~25 Hz。
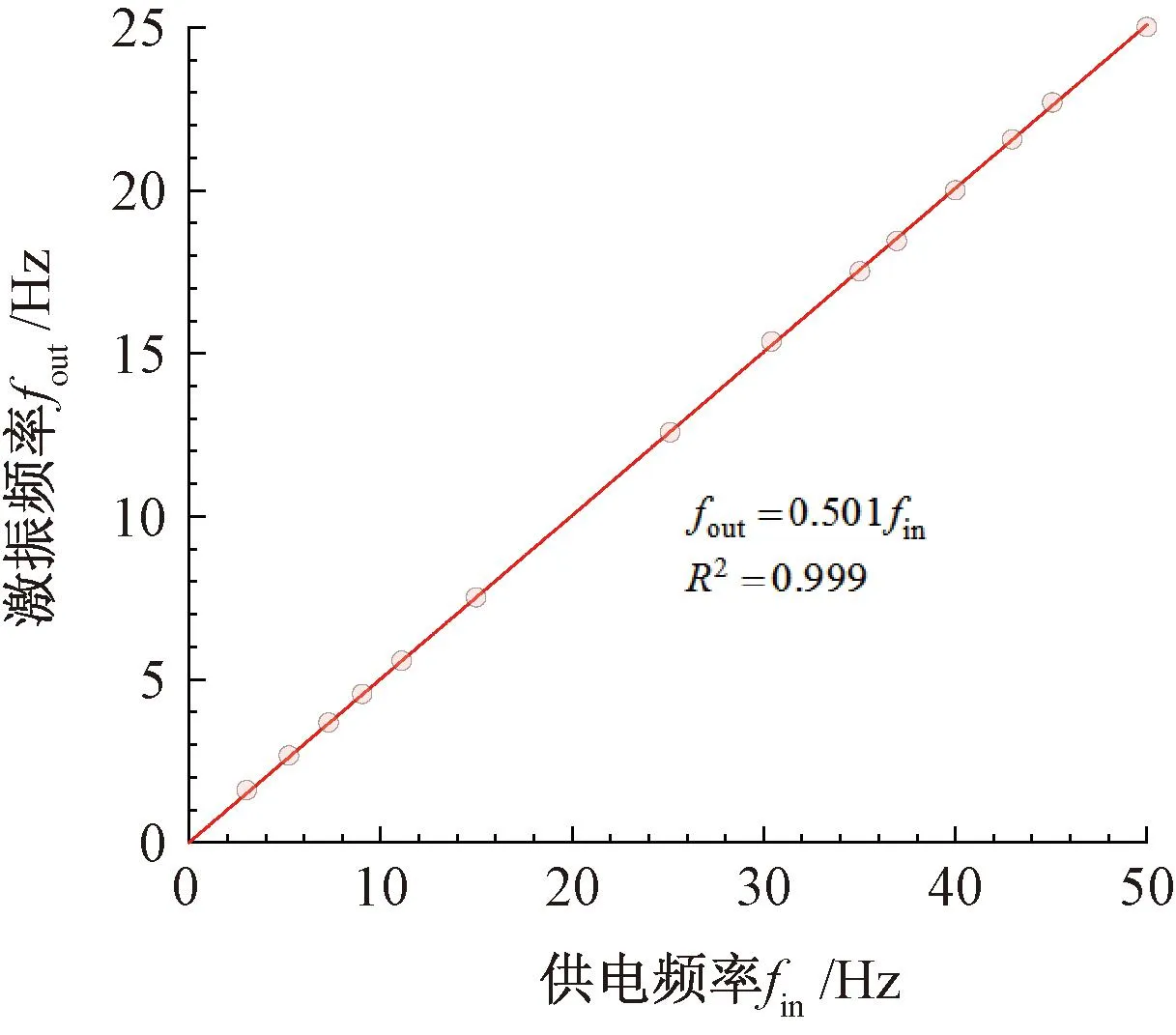
图5 激振频率标定曲线
4.2 激振力变化规律
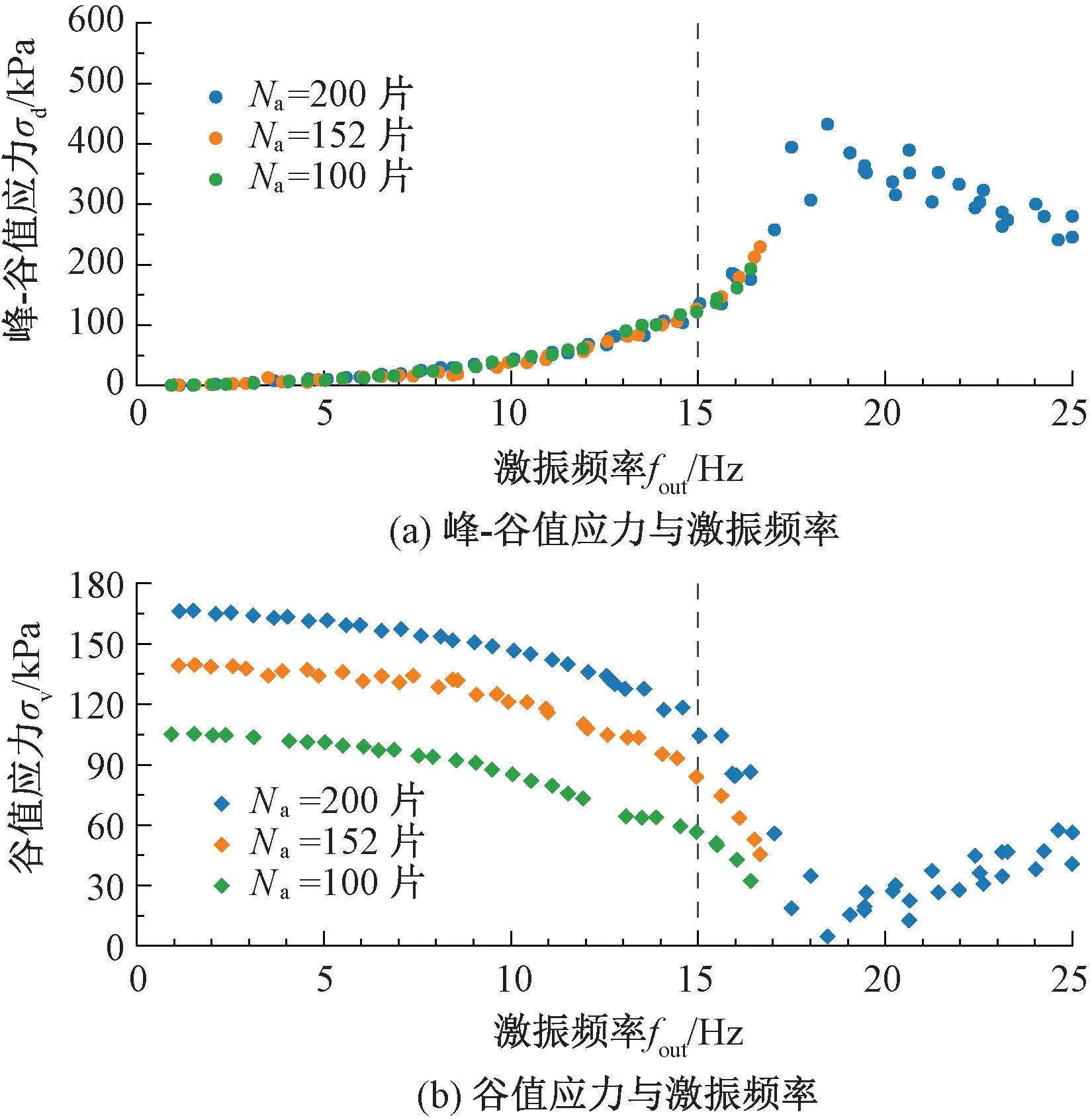
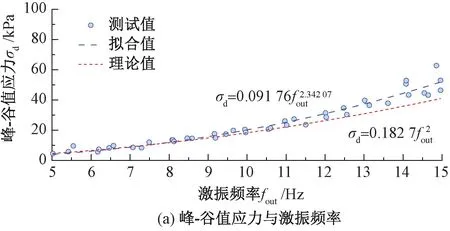
Na分别为200、152、100片时,σd、σv与fout关系曲线见图6~图8。由图6~图8可知,σd、σv随fout增加并不呈单调增加趋势,与理论上单调递增的二次曲线关系不符。在高配重(Na=200片)、少偏心片(Nc=4、8片)工况下,激振力曲线存在明显的上升及下降段,表现出共振现象;Nc=4、8片工况下,共振频率分别约为20、18 Hz;其他工况,由于配重不足,σv在fout<25 Hz时归零,未能实现满频率激振,未出现共振现象。仅就σd-fout曲线上升段(对应于σv-fout关系曲线下降段)而言,相同fout下,Nc越大,σd越大且σv越小,σd最高可达400 kPa。

图6 Na=200片配重下激振力与激振频率关系曲线

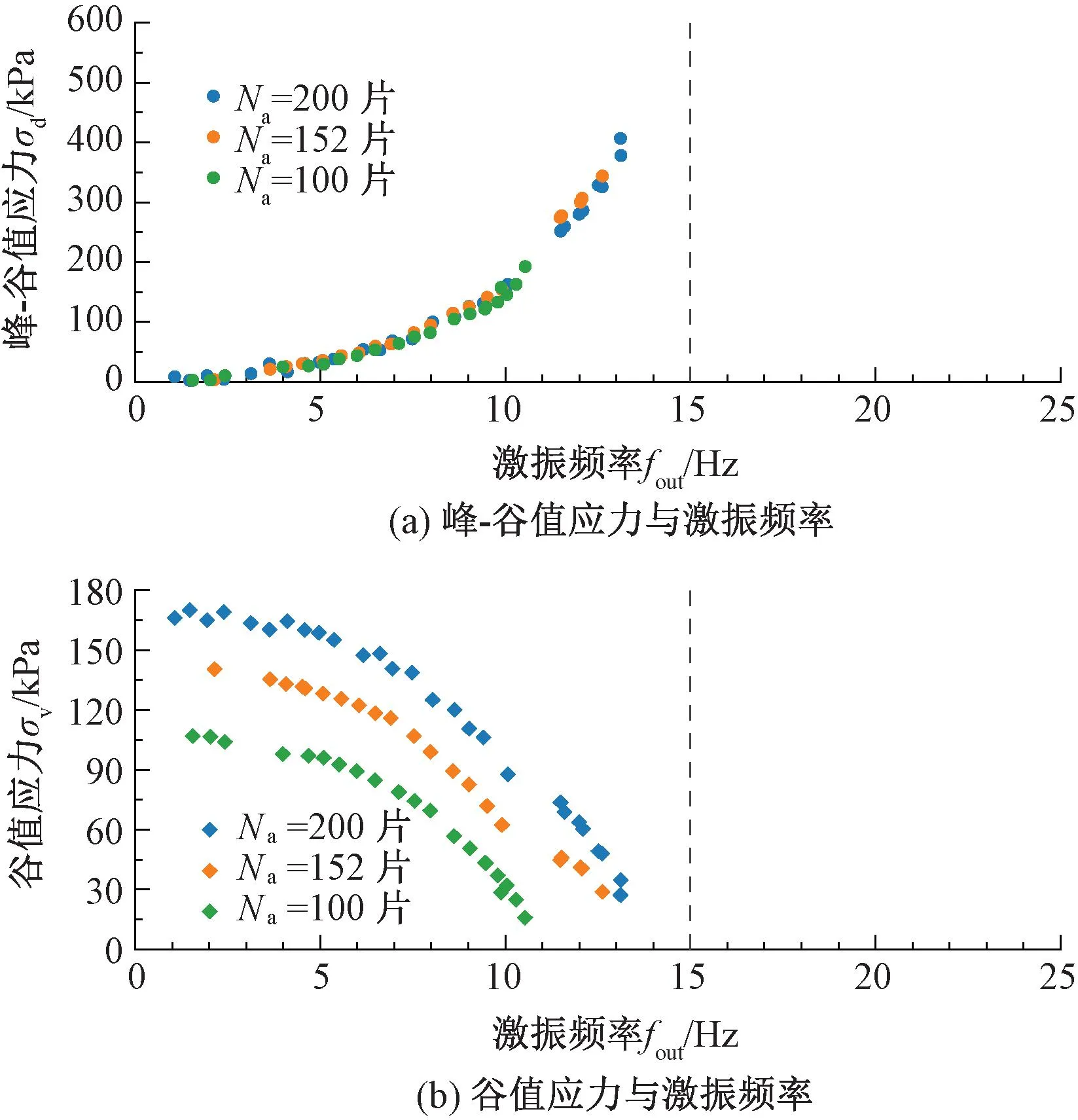
图7 Na=152片配重下激振力与激振频率关系曲线

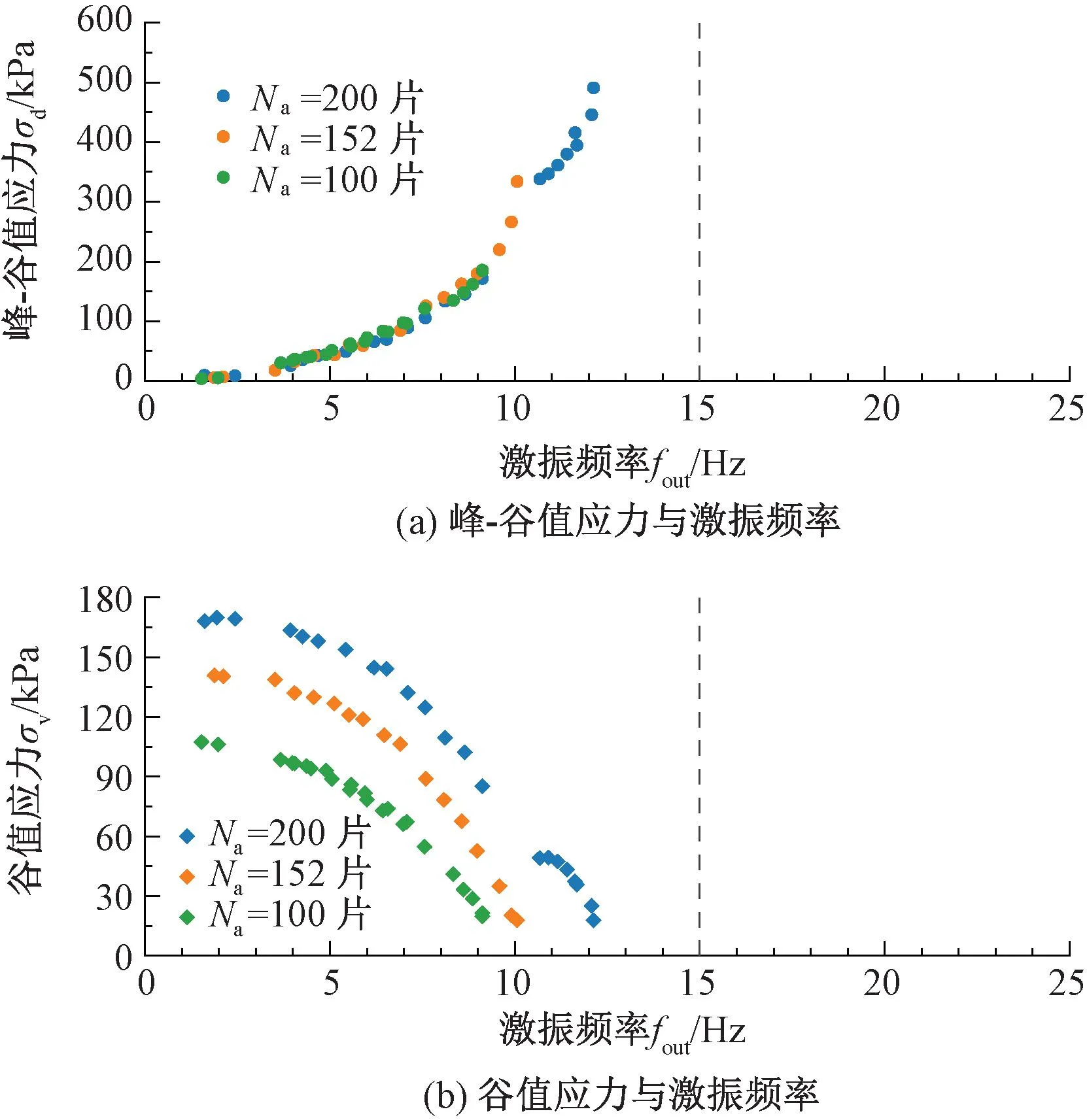
图8 Na=100片配重下激振力与激振频率关系曲线
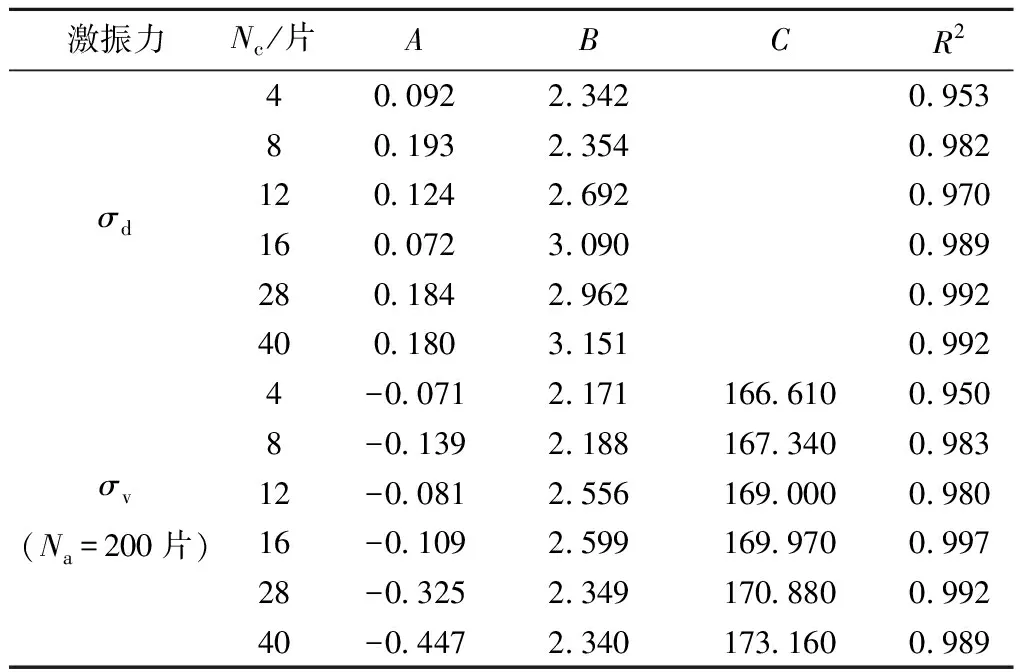
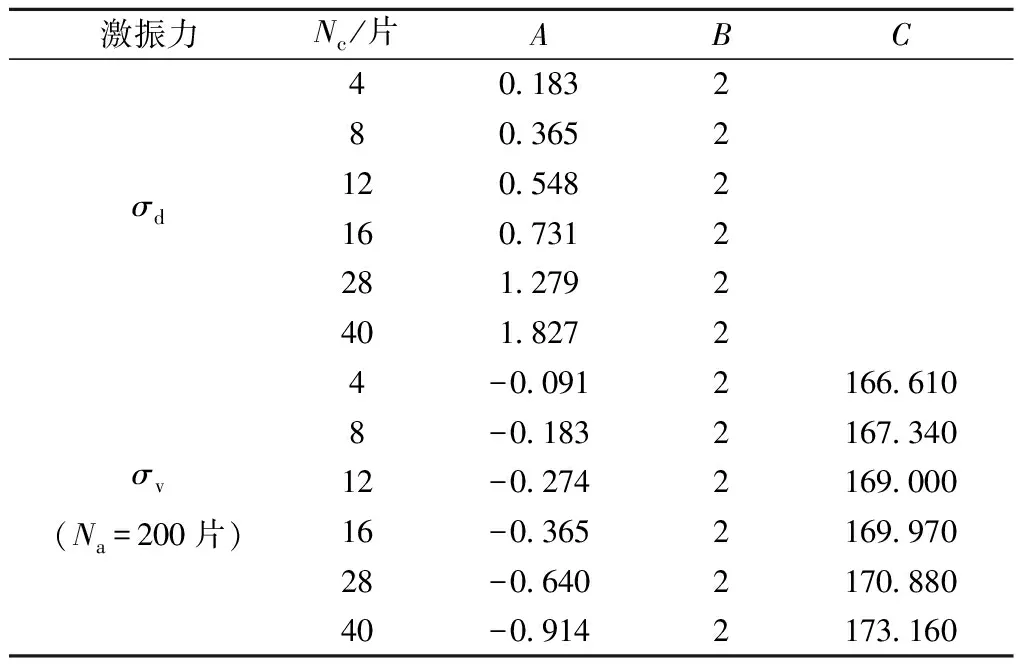
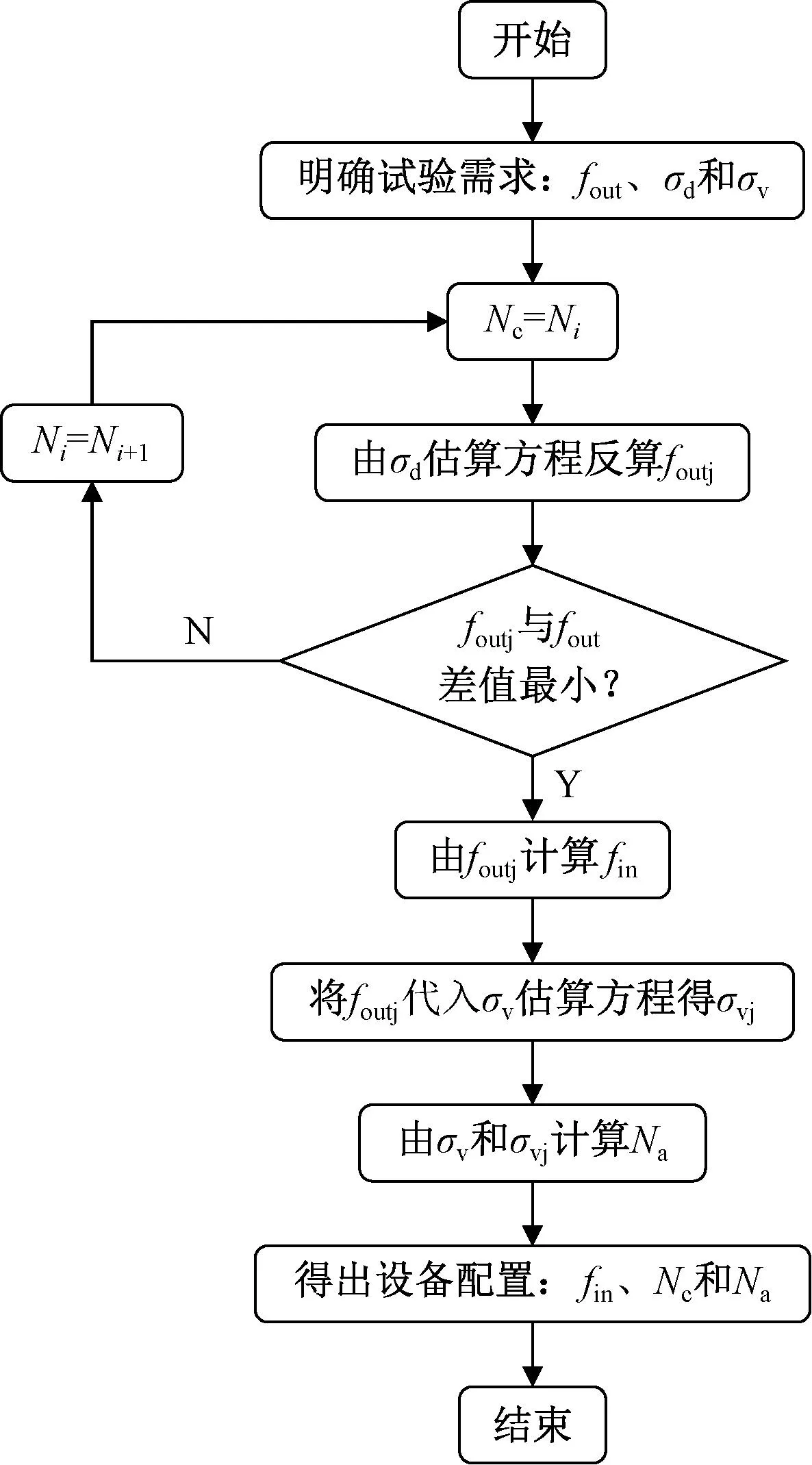
Nc分别为4、8、28、40片时,探讨Na对激振力的影响,σd-fout、σv-fout关系曲线见图9~图12。由图9~图12可知,当fout≤15 Hz且Nc相同时,不同Na的σd-fout曲线族基本重合,σv-fout曲线族相互平行。增减Na,使σv-fout曲线上下平移,对σd-fout曲线影响较小。由于受共振影响,当15 Hz 图9 1组偏心片(Nc=4片)下激振力与激振频率关系曲线 图10 2组偏心片(Nc=8片)下激振力与激振频率关系曲线 图11 7组偏心片(Nc=28片)下激振力与激振频率关系曲线 图12 10组偏心片(Nc=40片)下激振力与激振频率关系曲线 基于偏心质量旋转离心原理,激振力(σd、σv)与激振频率fout间具有二次函数关系,即 σd=8π2mcefout2 (14) σv=msg/S-4π2mcefout2 (15) 而二次函数可以看作是异速生长方程的特例,因此采用拟合激振力估算方程来表示,即 (16) 式中:A、B、C均为系数。 满配重(Na=200片)条件下,基于实测数据拟合确定的激振力估算方程系数及拟合优度见表5,所得估算方程曲线见图13。 表5 激振力估算方程系数及拟合优度 图13 激振力估算方程曲线 由式(14)、式(15)计算的激振力理论方程系数见表6。以Na=200片、Nc=4片工况为例,对比分析激振力测试值、估算值和理论值的差异,见图14。 表6 激振力理论方程系数 图14 Nc=4片时估算方程与理论方程的对比 由图14可知,σd测试值普遍高于理论值,而σv测试值普遍低于理论值,说明在振动电机下部安装内框架、配重块和加载板组成活动部件后,改变了振动电机原有的激振力输出水平,反映了开展激振装置现场标定试验的重要意义。激振力估算值拟合优度R2=0.953,可较好反映测试值数值水平,可用于指导设备配置和应用。其余偏心片配置工况下,规律与此一致。 基于对激振装置动态输出规律的分析,建立面向路基现场动测的设备配置方法流程,见图15。首先,明确激振试验模拟需求,包括fout、用于模拟路基动应力的σd和用于模拟轨道及上覆路基结构自重的σv。记表5和图13所涉及6种偏心片数量为估算方程所用偏心片数量Nci,i=1~6。即,Nc1=4片、Nc2=8片、…、Nc6=40片。将σd依次代入式(16)和表5,反算得到激振频率计算值foutj。选择与fout差值最小的foutj,由式(17)计算fin;相应条件下的Nci,即为偏心片配置数量Nc;将foutj代入式(16)和表5,得谷值应力计算值σvj,按式(18)计算配重块数量Na,Na应为4的整数倍。 图15 激振装置配置方法流程 fin=2foutj (17) (18) 研发了一套惯性式激振装置ISV400并开展现场标定,分析了fout与fin的关系,以及不同Nc、Na组合下σd、σv随fout的变化规律,得到了激振力估算方程,建立了一种设备技术配置方法。 1)fout与fin满足fout=0.501fin拟合关系,符合四极异步电机频率输出规律,由50 Hz电网工频换算的fout上限为25 Hz。测试表明,当fout<5 Hz时,电机自同步性较弱,装置运行欠平稳,激振力波形欠规整。 2)σd测试值高于根据偏心质量旋转离心原理计算的理论值,σv则相反,且偏差随fout增加而扩大。当fout>15 Hz时,部分Nc、Na组合下的σd随fout增加而先升后降(σv相反),相同Na关于Nc的σd-fout、σv-fout曲线族存在交叉,ISV400动态输出易受共振影响。 3) ISV400稳定工作频率区间为5~15 Hz,在此区间内,相同Na的σd-fout曲线族重合,不受Nc影响,σv-fout曲线族相互平行,随Nc变化而平移。实测结果表明,σd、σv随fout增加呈异速生长规律,基于激振力估算方程构建的设备配置方法可指导ISV400的使用。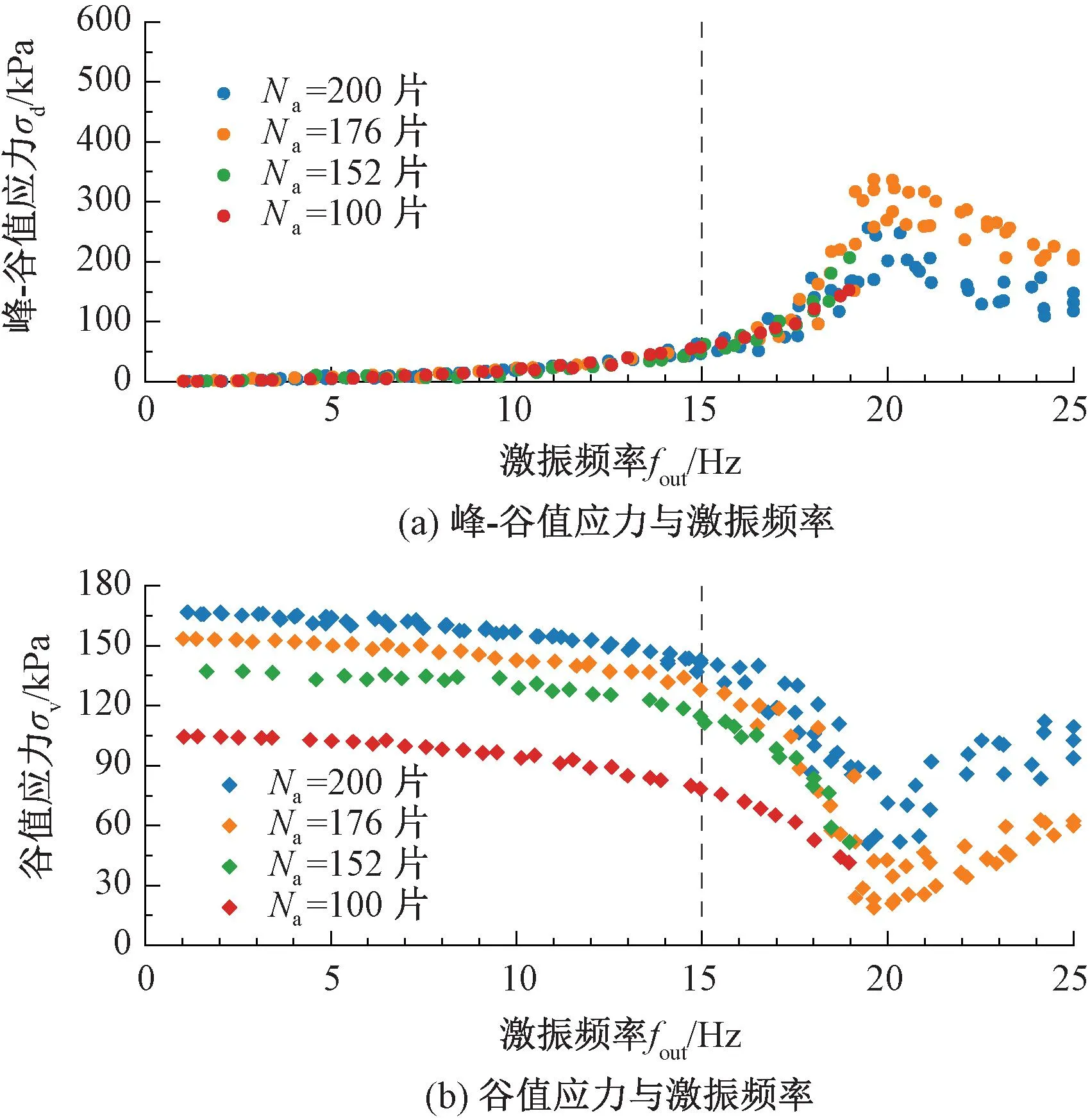
4.3 激振力估算方程


4.4 激振设备配置方法
5 结论

