夏季高温下支承层斜裂缝诱发纵连板上拱规律研究

张雅琴，高 亮，钟阳龙，蒋函珂，黄伊琛

(1.北京交通大学 土木建筑工程学院，北京 100044；2.北京交通大学 智慧高铁系统前沿科学中心，北京 100044；3.中国铁路经济规划研究院有限公司 铁路工程技术标准所，北京 100038)

CRTSⅡ型板式无砟轨道作为全线纵连结构,采用6根精轧螺纹钢筋纵向连接,具有较好的稳定性、平顺性,广泛应用于京津城际、武广、京沪等线路[1]。纵连式结构在高温环境无法自由伸缩,内部集聚温度力可达上千吨。当温度力达到纵连式无砟轨道结构薄弱部位如层间界面、宽窄接缝极限应力强度时,极易出现稳定性衰减甚至丧失。刘付山等[2]基于CRTSⅡ型板式无砟轨道上拱变形分析模型,研究了施工过程中轨道板上拱变形规律以及温度梯度对轨道板竖向上拱临界温升幅度的影响。周敏等[3]分析温度作用下桥上纵连板式无砟轨道离缝发展规律及变形产生原因。Ren等[4]考虑了轨道板自重和初始偏心的影响,基于能量法的解析表达式,研究了轨道上拱发展的过程。陈龙等[5]采用内聚力模型模拟轨道板和砂浆层的黏结关系,分析了温度梯度荷载作用下层间破坏规律。Zhu等[6]通过试验研究了无砟轨道层间界面本构关系和疲劳性能,并利用基于试验的分析模型研究了单调和周期温度梯度荷载下层间界面的损伤演化。钟阳龙等[7]利用层间剪切破坏有限元模型,分析了不同整体升温荷载作用下层间剪切破坏过程。Cai等[8]从结构失稳角度研究了板端接缝处的上拱机理,并分析了接缝混凝土的破坏过程及其对轨道板上拱的影响。高亮等[9]考虑材料非线性,研究了不同整体升温幅度下层间黏结状态和板间接缝状态对上拱变形的影响。赵国堂等[10]对轨道板在日温差、年温差和冲击荷载等循环作用下,上拱离缝发生、发展机理进行了仿真分析。Huang等[11]研究了宽窄接缝和界面损伤共同作用下的轨道结构上拱变形。

以上研究多关注宽窄接缝缺损和层间离缝引发的轨道结构上拱,工务人员现场检查发现,支承层斜裂病害频繁出现。支承层斜裂缝一旦贯通,在夏季高温作用下有上拱风险,也会出现CA砂浆离缝、轨道板开裂和宽窄接缝破损等次生病害,从而影响轨道结构稳定性。目前,对CRTSⅡ型板式无砟轨道支承层斜裂病害的研究已取得一定成果。赵坪锐等[12]分析了不同裂缝间距、支承层厚度和弹性模量下双块式无砟轨道开裂支承层的折减弹性模量。杨荣山等[13]分析了支承层开裂对双块式无砟轨道整体刚度、支承层和道床应力的影响。刘薇[14]分析了温度荷载作用,基础不均匀沉降,轨道板纵向不连续和支承层底部脱空四种工况下支承层的受力特征。黄传岳[15]对CRTSⅡ型板式无砟轨道支承层斜裂伤损,提出了成套的修复工艺流程。张志远[16]提出了基于绳锯切割的支承层斜裂修复技术。温浩等[17]通过对支承层斜裂修复后的服役状态动力学监测和无损检测,对修复效果进行整体评价。但以上研究多考虑支承层开裂对于弹性模量、结构整体刚度和受力的影响,对支承层斜裂病害多关注伤损后的修复工艺以及修复后效果评价,很少涉及支承层斜裂缝在温度力作用下对纵连轨道结构服役状态的影响。因此,有必要研究支承层斜裂伤损无砟轨道在高温下的受力状态、上拱变形和次生病害。

为此,本文基于内聚力理论和塑性损伤理论建立带有支承层斜裂缝的CRTSⅡ型板式无砟轨道三维模型,研究高温下支承层斜裂损伤无砟轨道的温度力作用,分析无砟轨道受力状态、支承层错动导致的上部结构上拱变形形态、轨道结构二次伤损情况及结构服役状态随温度的演化。研究结果可为支承层斜裂缝诱发的CRTSII型板式无砟轨道上拱病害整治维修提供依据,为保障我国高速铁路安全平稳运营提供参考。

1 计算模型及参数

本文建立的CRTSⅡ型板式无砟轨道精细化有限元模型,利用内聚力单元模拟轨道层间相互作用,采用混凝土塑性损伤模型分析支承层斜裂缝导致的轨道结构伤损,轨道板内建立钢筋网以模拟轨道板的受力变形,支承层考虑伸缩假缝来细化支承层服役状态。

1.1 内聚力模型

根据现场实测,在夏季高温时段,支承层斜裂伤损无砟轨道的轨道板与CA砂浆层之间、CA砂浆层与支承层之间、宽窄接缝与轨道板之间均发生不同程度的离缝。采用双线性内聚力模型[18-19](cohesive zone model,CZM)来表征其损伤开裂关系。双线性内聚力模型的本构关系曲线见图1。双线性内聚力模型的拉力-位移关系[20-21]为

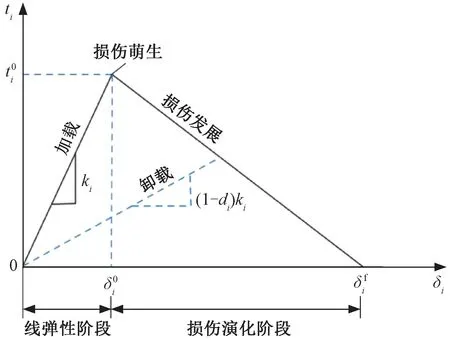
图1 双线性内聚力本构曲线

( 1 )

根据界面内聚强度与界面相对位移的关系,界面刚度ki可表示为

( 2 )

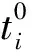
在开裂的初始阶段,层间界面无损伤产生,当界面相对位移达到一定程度后,层间界面开始产生损伤。界面刚度随界面相对位移的增加而减小,通过引入损伤因子di来定量描述界面损伤程度[18,20],即

( 3 )

式中:δimax为加载历史中所达到的最大界面相对位移值;di为损伤因子,取值范围为0～1,当di=0时,表明界面未伤损,层间粘结完好,当di=1时,表明界面完全失效,层间开裂。

界面临界断裂能φi为拉力-位移曲线与坐标轴所围成的面积,可表示为

( 4 )

1.2 混凝土塑性损伤模型

为分析支承层斜裂上拱造成的宽窄接缝损伤和轨道板开裂,采用混凝土塑性损伤(concrete damage plastic,CDP)模型[22]来模拟无砟轨道结构轨道板和宽窄接缝的塑性变形和刚度退化。混凝土在荷载作用下进入应力-应变曲线的软化段卸载时,混凝土材料发生刚度退化,可以用抗拉、抗压损伤因子dt、dc来表征混凝土材料的刚度退化。CDP模型本构曲线见图2。图2中,σt0、σc0、σcu分别为混凝土受拉屈服强度、受压屈服强度、受压峰值强度,其本构关系为

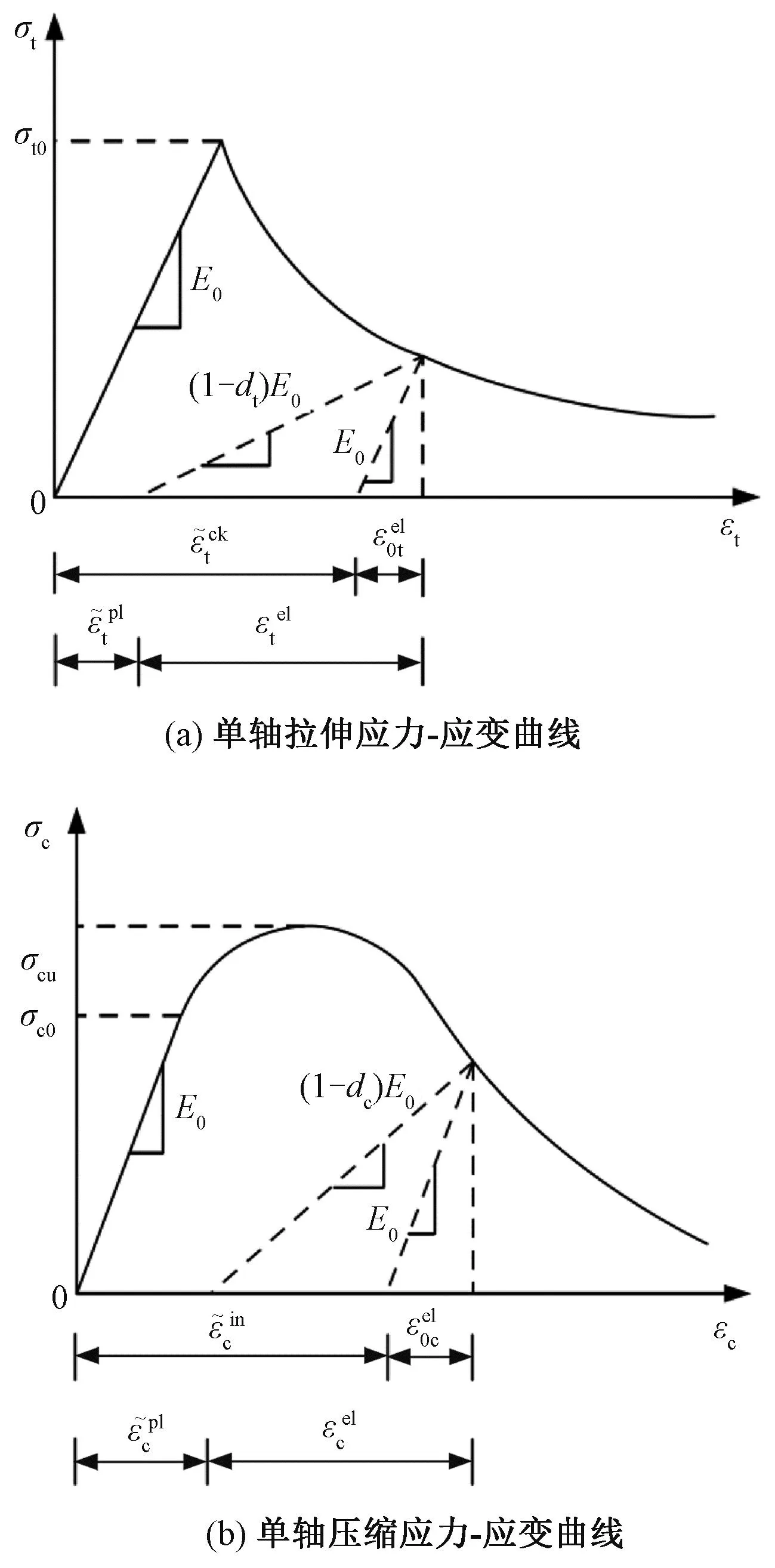
图2 混凝土塑性损伤模型本构曲线

( 5 )

( 6 )

式中:σt、σc分别为混凝土的受拉、受压应力;εt、εc分

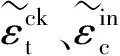
( 7 )

( 8 )

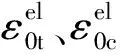
1.3 支承层伸缩假缝

为减少大体积混凝土施工中常出现的水化热引起的裂缝,在混凝土基层浇筑后12 h内每隔5 m设置一道伸缩缝。接缝深度应大于混凝土基层厚度的1/3,一般为105 mm,宽度不应超过5 mm。为模拟温度作用下混凝土基层斜裂缝损伤后的受力状态,细化支承层模型结构,模型中每隔5 m设一条高度为105 mm的伸缩缝。

1.4 钢筋网

由于轨道板内配有普通钢筋、横向预应力筋和纵连预应力筋,对轨道结构的受力、变形和整体性有重要影响,因此对轨道板中的钢筋进行模拟。6根直径为20 mm的精轧钢筋置于预制板中,形成纵向连接体系。预制板中有60根单层横向预应力钢筋。普通钢筋分层布置,并设置40 mm厚混凝土保护层[23]。每根横向预应力钢筋的设计拉力为68.3 kN。单根精轧钢筋的设计拉力为50 kN。利用Abaqus初始应力法模拟钢筋的预应力。

1.5 整体模型

建立总长度为45.45 m的CRTSⅡ板式无砟轨道精细化模型。由于无砟轨道横向轴对称的特点,为提高计算效率,采用1/2模型仿真。钢轨、预制板、宽窄缝、张拉锁件、CA层、支承层和路基均采用实体单元C3D8R模拟,钢筋采用桁架单元T3D2模拟,扣件利用三向非线性弹簧模拟,扣件间距0.65 m。轨道板与CA砂浆层、轨道板与宽窄接缝、宽窄接缝与CA砂浆层、CA砂浆层与支承层界面均采用内聚力接触模拟,支承层与路基,支承层伸缩假缝,支承层斜裂贯通断缝界面采用摩擦接触。模型两端和中心对称面为对称约束,路基底部完全固定。整体模型见图3。

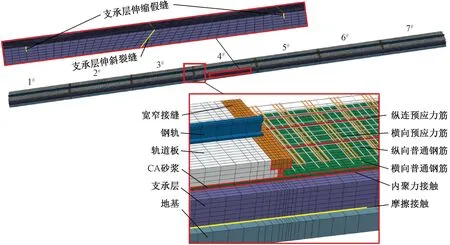
图3 CRTSⅡ型板式无砟轨道支承层斜裂缝分析模型

1.6 模型参数

轨道板长为6.45 m,宽为1.275 m,高为0.2 m。CA砂浆层宽为1.275 m,高为0.03 m。支承层宽为1.475 m,高为0.3 m。路基宽为1.6 m,高为0.2 m。宽接缝宽为0.21 m,高为0.1 m。窄接缝宽为0.05 m,高为0.1 m。为消除边界效应,模型选取7块相邻轨道板进行计算,并取中间轨道板进行分析。内聚力参数取值见表1[1,24]。CRTSⅡ型板式无砟轨道结构材料参数见表2[1,24]。

表1 内聚力模型参数

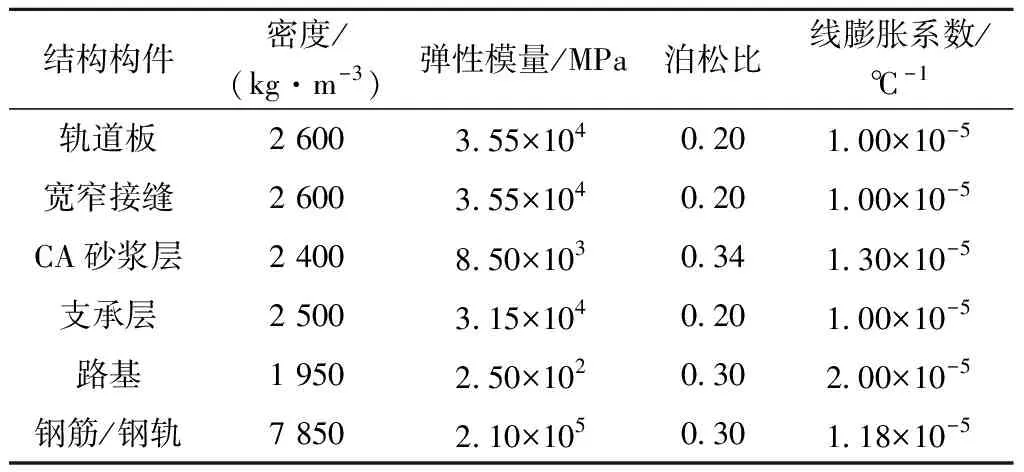
表2 CRTSⅡ型板式无砟轨道结构材料参数

1.7 模型验证

本文通过内聚力模型、混凝土塑性损伤模型验证,并与文献模型计算结果对比进行整体模型验证和现场实测结果的对比验证来证明模型的有效性。

通常采用推板试验[7,11]来验证内聚力模型参数的可靠性,本文参照推板试验条件建立有限元模型,该模型与本文模型建立过程相似。推板仿真模型板长取单块板,模型一侧边界条件自由,另一侧施加位移荷载。仿真计算结果与实测结果对比见图4(a)。由图4(a)可知,仿真计算结果与实测结果吻合度较好,表明了本文内聚力参数取值的有效性。

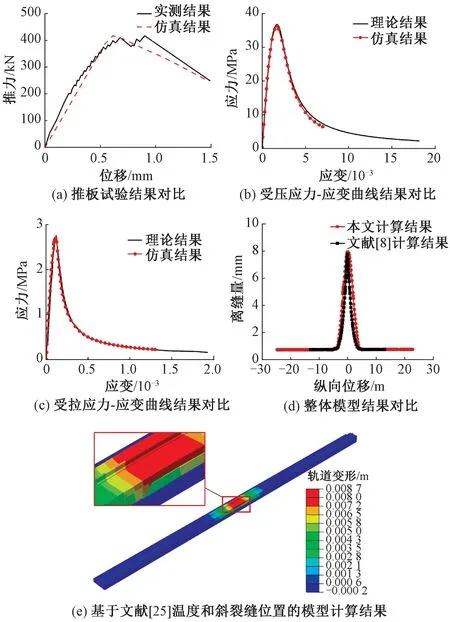
图4 模型验证结果

利用有限元软件模拟混凝土标号为C55的标准立方体试件加载试验来验证本文采用的混凝土塑性损伤模型的有效性。通过对立方体试件施加位移荷载,得到的应力-应变曲线见图4(b)和图4(c),其与理论结果吻合较好,表明本文采用的混凝土塑性损伤模型参数的可靠性。

将本文不含斜裂缝的完整模型和文献[8]的计算模型对比,在相同约束,正温度梯度荷载均为90 ℃/m,宽窄接缝处横向损伤长度为1.275 m,损伤高度为0.12 m,混凝土标号为C35时,轨道板与CA砂浆离缝值的文献[8]与本文完整模型计算结果对比见图4(d),表明本文完整模型的可靠性。

根据京沪高速铁路工务人员2016年7月23日检查发现,第二、三承轨台位置支承层斜裂破损,轨道板上拱9 mm[25]。综合实测气温与无砟轨道温度场关系[26-28],设置与文献[8]相同的温度荷载。在温度和斜裂缝位置相同的情况下,模型计算结果见图4(e),轨道最大变形8.7 mm,与现场实测结果吻合较好,验证本文考虑支承层斜裂缝模型的有效性。

2 计算结果分析

本文从斜裂缝破损高度、温度变化、斜裂缝与轨道板纵向相对位置、斜裂缝起裂角度四方面来开展夏季高温下支承层斜裂缝诱发纵连板上拱规律研究。根据夏季高温下高速铁路路段实测数据[27],极端高温下,轨道结构垂向温度在轨道板和CA砂浆层呈现明显的非线性特征,最高温梯可达100 ℃/m,支承层垂向温度变化较小。支承层最高温度40 ℃,轨道板表面最高温度60 ℃。综合文献[27]实测数据取轨道结构整体升温40 ℃,轨道板和CA砂浆层温度梯度100 ℃/m。模型温度取值对实测温度数据具有较好的包络,见图5。结合文献[15-16,25]和纵连板服役现状分析,将斜裂缝破损高度H作为变量来研究斜裂缝破损程度对纵连板上拱规律的影响,见图6。对斜裂缝与轨道板纵向相对位置取斜裂缝破坏典型位置,即板端、1/4板长、1/2板长来研究斜裂缝破坏对纵连板上拱规律的影响,见图7。据现场检查结果[15-16,25],斜裂缝角度α多呈30°～45°,为研究裂缝破损角度对纵连板上拱规律的影响,取15°、30°、45°、60°、90°斜裂缝进行计算,见图8。

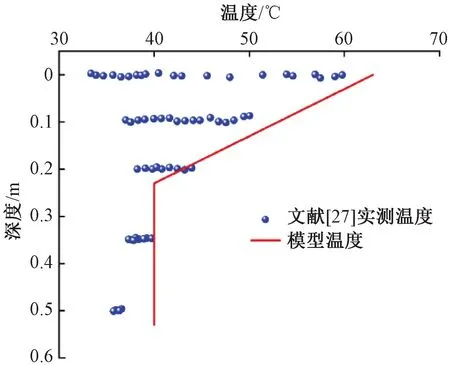
图5 轨道结构文献实测温度与模型温度对比

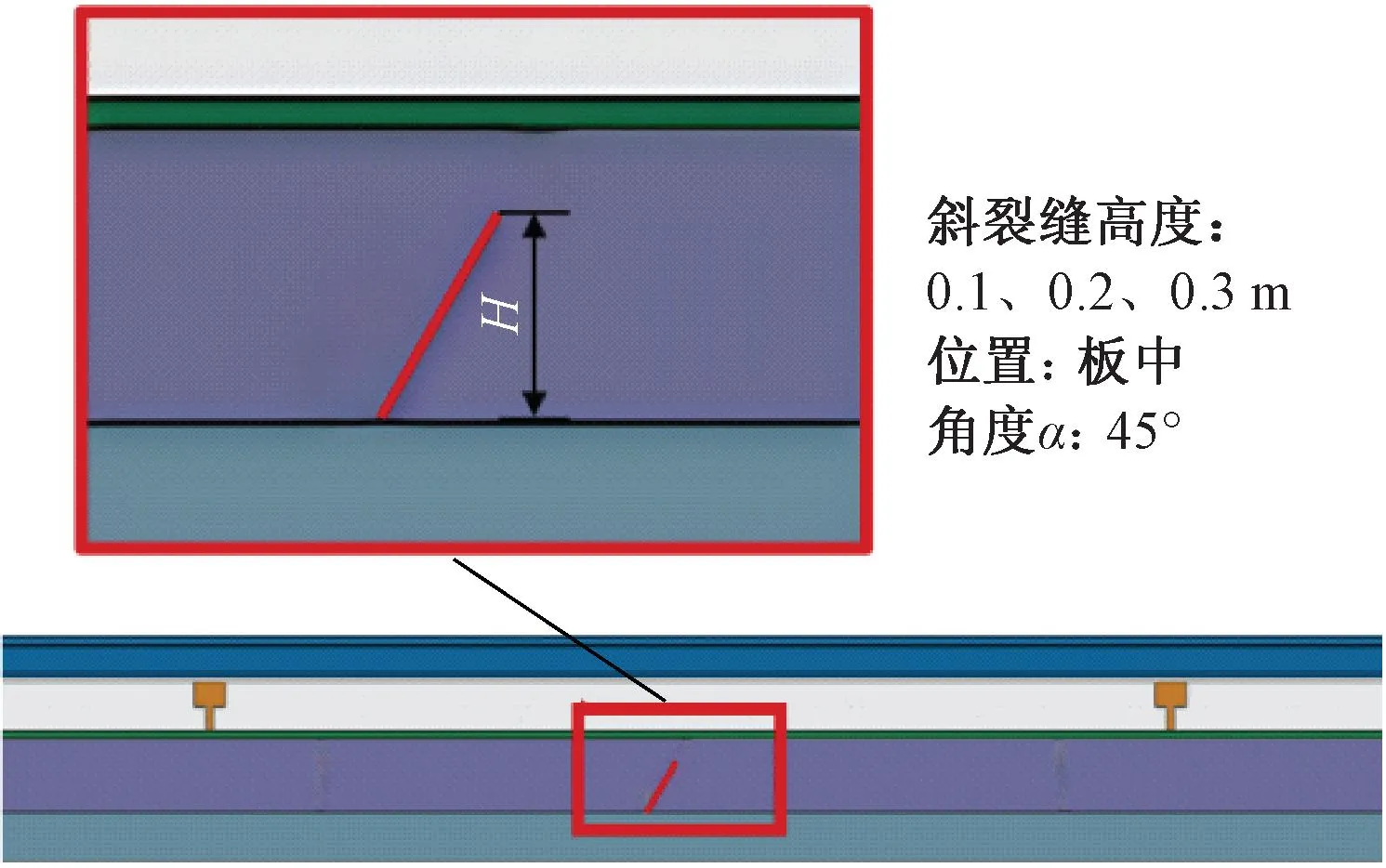
图6 支承层斜裂缝高度示意

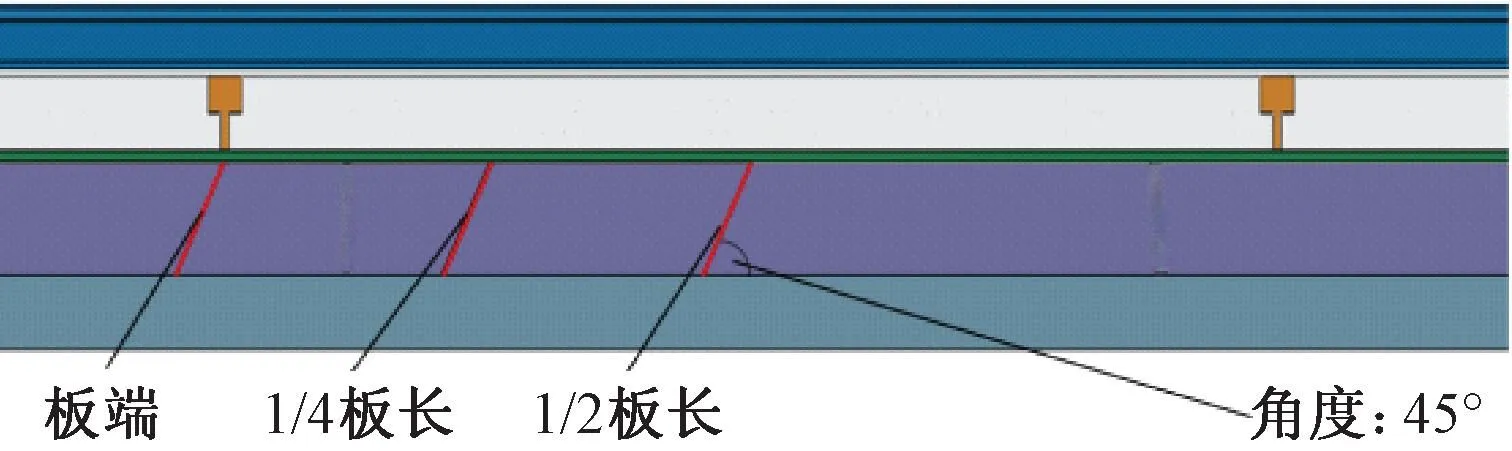
图7 支承层斜裂缝位置示意

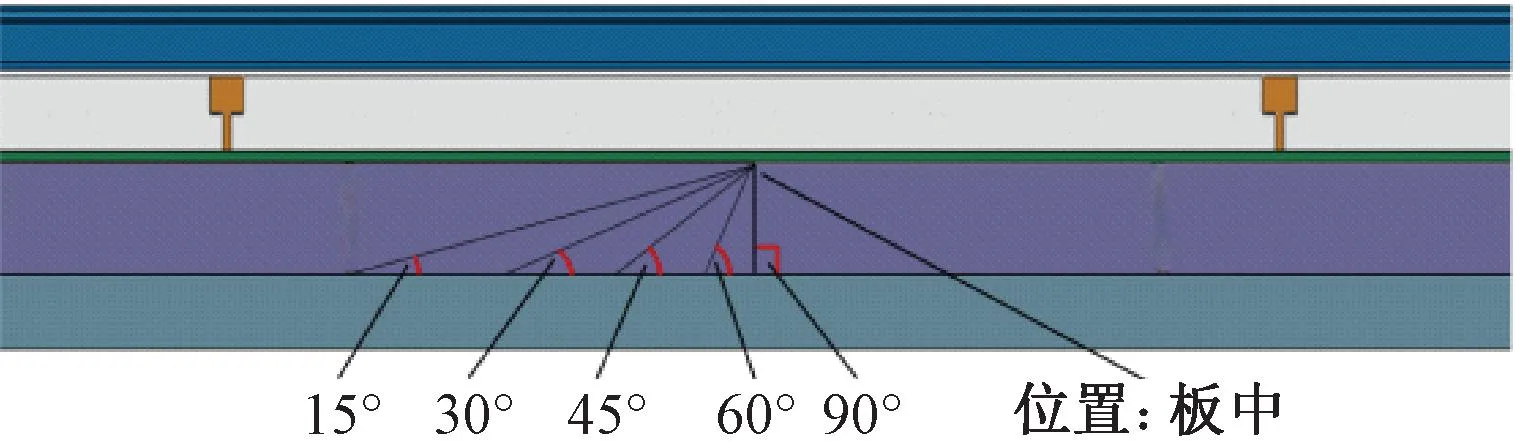
图8 支承层斜裂缝角度α示意

2.1 斜裂缝高度影响

在极端高温作用下,斜裂缝纵向相对位置位于板中,起裂角度为45°时,用斜裂缝破损高度0.1、0.2、0.3 m对应支承层斜裂缝1/3破损、2/3破损和完全破损,来衡量斜裂缝破损程度对轨道结构变形与受力的影响,见图9、图10。

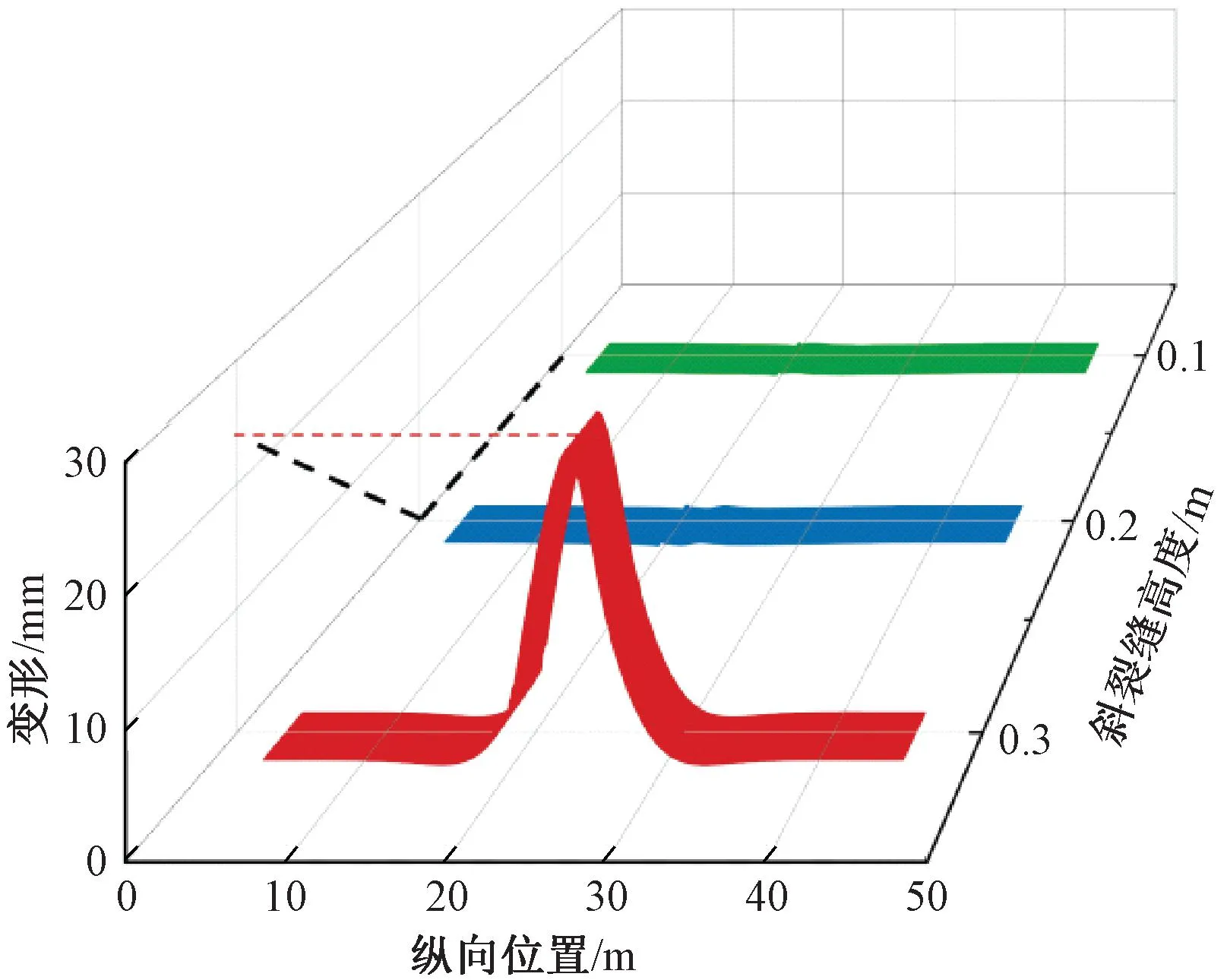
图9 轨道结构变形随斜裂缝高度变化

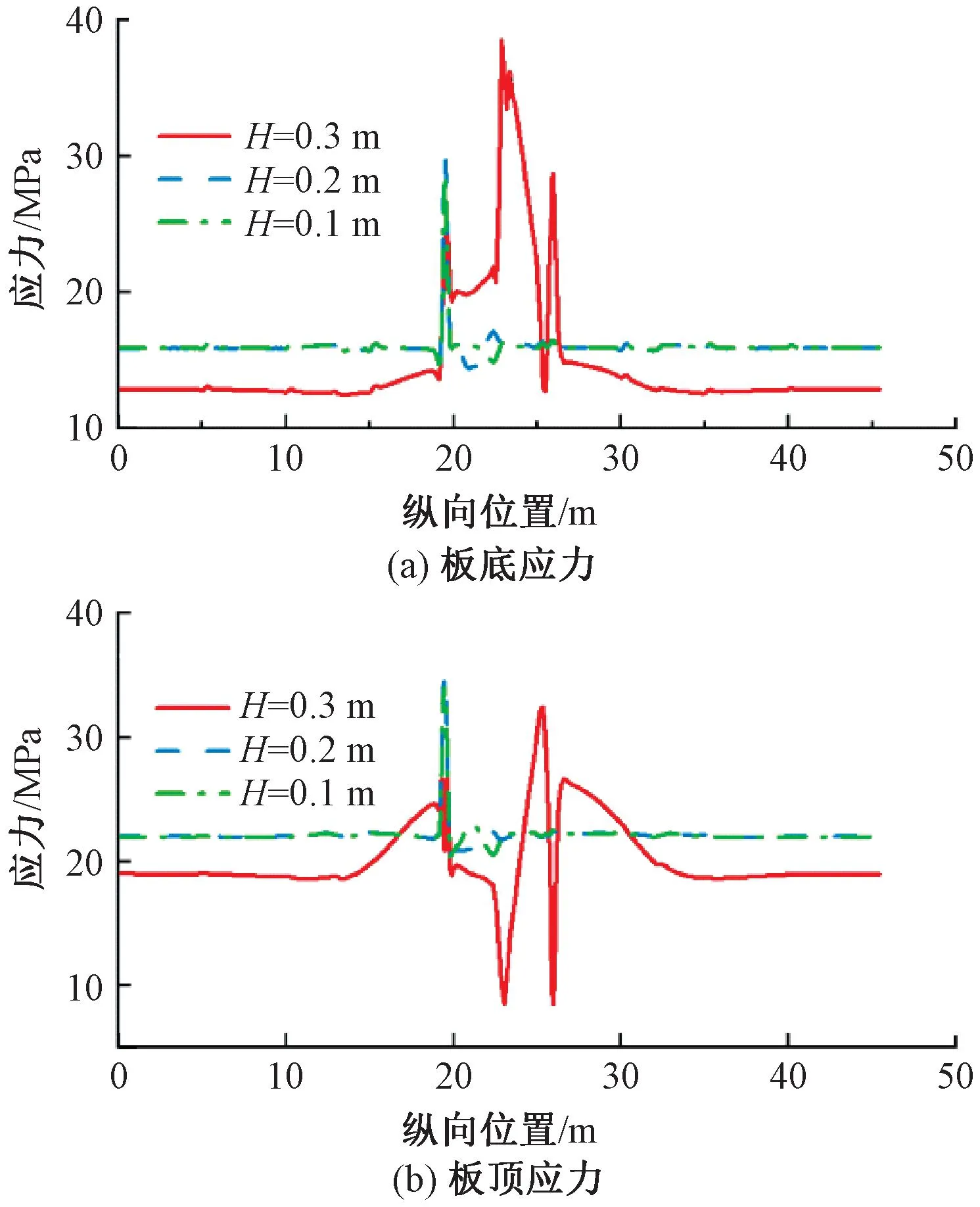
图10 轨道板顶、底应力

由图9可见,斜裂缝破损高度H为0.1、0.2、0.3 m时,轨道结构变形分别为0.35、0.40、24.3 mm。当斜裂缝未完全破损时,斜裂缝破损程度对轨道结构上拱变形影响较小,高温作用下对轨道结构上拱变形影响均较小,斜裂缝上方的轨道板和支承层上翘端的宽窄接缝均产生较小的上拱变形。斜裂缝一旦贯通,相同温度力作用下,轨道结构变形急剧增大。因此现场检查需重点关注贯通斜裂缝。

由图10可见,当轨道结构处于完好状态时,在极端高温作用下,轨道板处于小偏压受力状态,从板底到板顶,轨道板压应力逐渐增大,均处于C55混凝土抗压强度标准值35.5 MPa范围内,结构受力状态良好。支承层斜裂缝的出现,导致支承层上翘端的宽窄接缝顶面和底部应力突变,当斜裂缝破损高度为0.1、0.2 m时,轨道结构变形分别为0.35、0.40 mm,宽窄接缝表面最大应力分别为34.0、34.8 MPa,宽窄接缝顶部存在受压破损风险。当斜裂缝破损高度为0.3 m,两侧支承层完全脱开时,改变了轨道上部结构纵连受力状态,斜裂缝远端轨道板受力有所减小,应力向斜裂缝所在位置集中,在斜裂缝周围两块板长范围内,轨道板应力震荡突变。在支承层斜裂贯通缝影响下,斜裂缝附近板底应力局部大于板顶应力,超过C55混凝土抗压强度标准值,轨道板底受压破坏,轨道上拱变形急剧增大至24.3 mm。

2.2 温度变化影响

利用斜裂缝位置位于板中、起裂角度为45°的斜裂贯通缝模型来研究温度变化对于轨道结构变形离缝的影响,见图11。由图11可知,随轨道结构整体温度升高,支承层斜裂缝断面相互错动,形成支承层斜断面一侧上翘,一侧下拱的形态,下拱端CA砂浆层和支承层撕裂。当整体升温20 ℃时,轨道结构上拱变形3.4 mm,CA砂浆层与支承层离缝、支承层斜裂缝断面错动、支承层与路基离缝三种伤损同时出现。随轨道结构整体升温进一步提高,轨道结构上拱变形增加,当整体升温40 ℃时,轨道结构上拱变形16.3 mm,支承层上翘端轨道板与CA砂浆层出现离缝。当轨道板进一步施加100 ℃/m正温度梯度时,在温度梯度带来的轨道板翘曲效应耦合下,轨道结构上拱效应进一步加剧,轨道结构上拱变形24.2 mm,支承层上翘端轨道板与CA砂浆层离缝、支承层下拱端CA砂浆层与支承层离缝、支承层与路基离缝都显著增加。因此,轨道结构变形随温度变化规律为支承层斜斜裂缝相互错动引发支承层与路基、CA砂浆层与支承层离缝,随轨道结构上拱变形加剧,轨道板与CA砂浆层离缝随之出现。

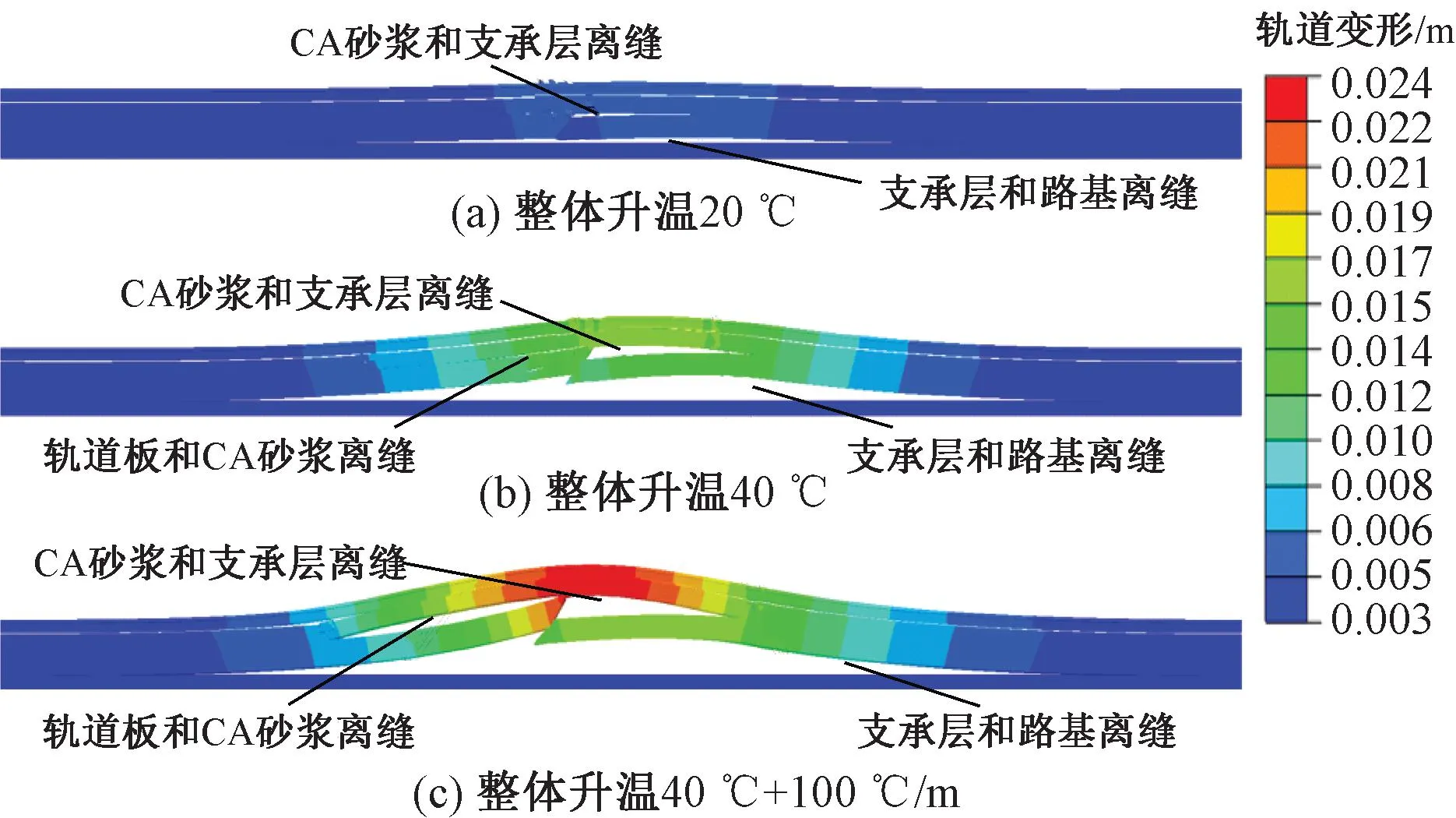
图11 轨道结构竖向变形云图(变形放大系数30)

利用轨道结构变形离缝、轨道板和宽窄接缝拉压、刚度平均损伤因子来研究轨道结构随整体升温演化趋势,见图12。由图12可知,整体升温小于10 ℃时,此阶段温度压力较小,温度力产生的上拱分力与轨道结构自重和斜裂缝截面的摩擦力处于自平衡状态,轨道结构几乎不产生上拱变形。当整体升温为10～20 ℃时,轨道结构变形0.8～3.4 mm,轨道板和宽窄接缝均处于弹性阶段,轨道结构变形和伤损发展缓慢。当整体升温在20～30 ℃时,轨道结构变形、支承层与路基离缝、CA砂浆层与支承层离缝分布分别为3.4～8.0、2.7～6.1、1.6～3.2 mm,轨道板和宽窄接缝开始进入塑性阶段,轨道结构变形和伤损加速发展。当整体升温大于30 ℃时,轨道板与CA砂浆层离缝逐步出现,轨道结构变形、支承层与路基离缝、CA砂浆层与支承层离缝进一步增大,轨道板和宽窄接缝拉压伤损加剧,轨道结构变形和伤损进入飞速破坏阶段。因此,支承层斜裂贯通缝诱发的轨道结构变形与伤损可分为0～20 ℃的缓慢发展阶段、20～30 ℃的加速发展阶段和大于30 ℃的飞速破坏阶段。根据无砟轨道结构温度分布与环境温度的关系[26-28],建议环境温度大于30 ℃时,加强对支承层斜裂贯通缝的检查。

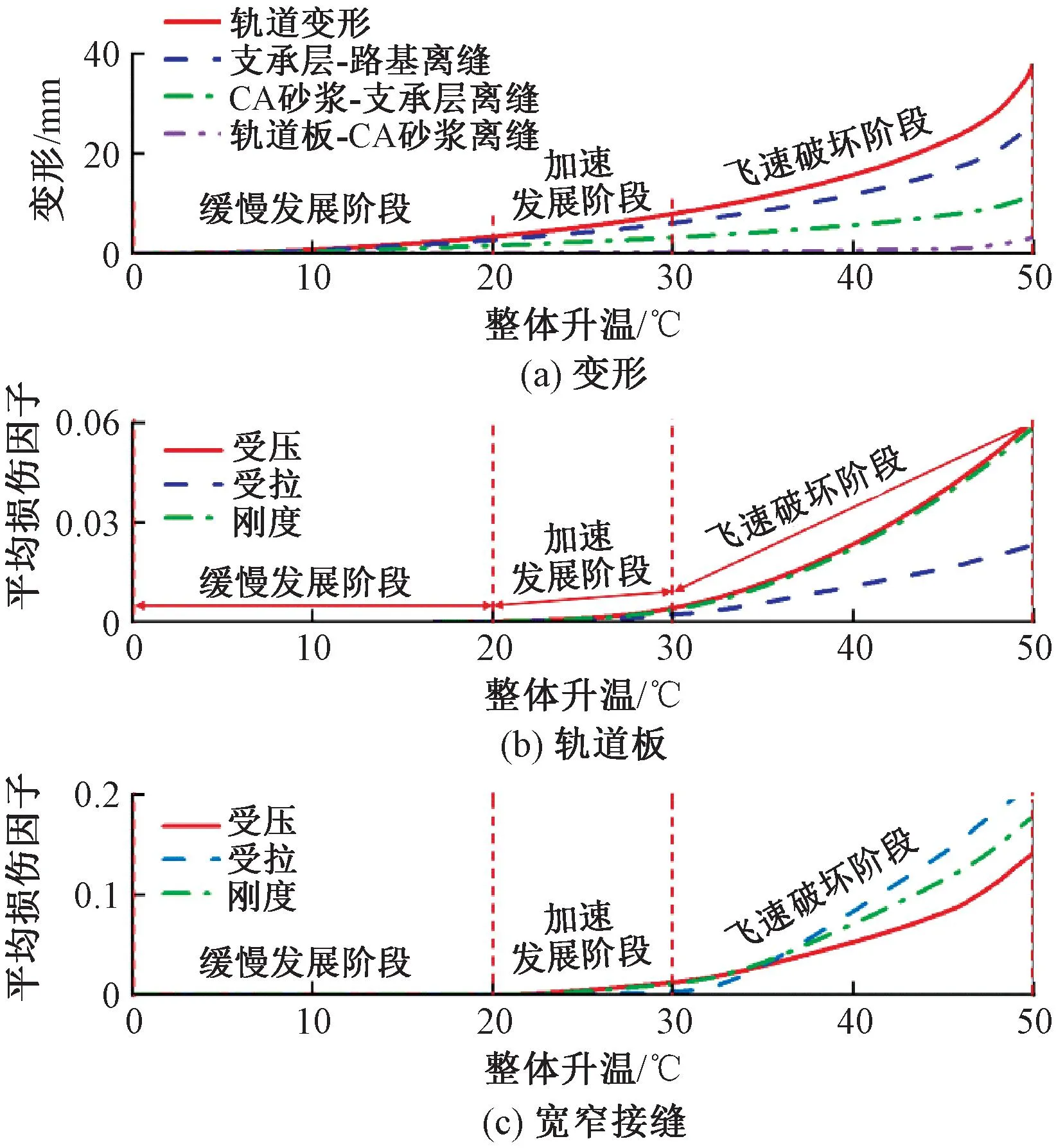
图12 轨道结构变形和伤损随温度变化规律

2.3 斜裂缝位置影响

利用45°斜裂贯通缝位于不同纵向相对位置模型研究轨道结构变形与伤损随斜裂缝位置变化规律,见图13。

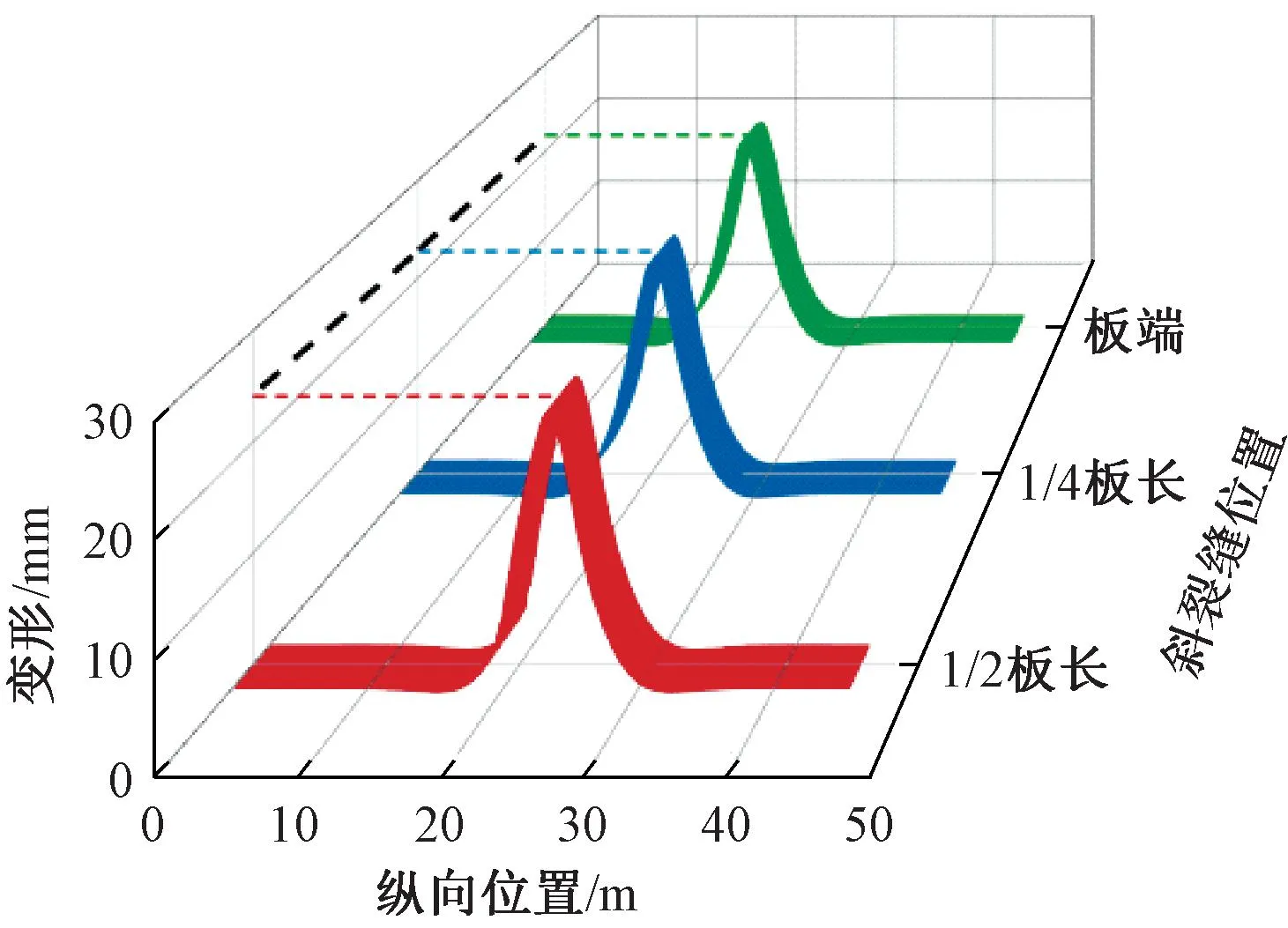
图13 轨道结构变形随斜裂缝位置变化

由图13可知,在极端高温作用下,45°斜裂贯通缝位于板端、1/4板长、1/2板长时轨道结构变形分别为22.2、23.1、24.2 mm,随斜裂缝向板中靠近,轨道结构受力偏于不利,轨道结构变形略微增大。结合CA砂浆隐蔽性施工的实际情况和CA砂浆与轨道板离缝频发的服役状况,在极端高温作用下,轨道板的受力可简化为宽窄接缝为支座的小偏心受压连续板。当斜裂缝纵向相对位置从板端向板中变化时,上拱力从“支座”向“跨中”移动,结构上拱变形逐步增大。因此现场检查需重点注意斜裂贯通缝发生在板中的轨道结构变形。

轨道板底受压损伤云图见图14。由图14可知,在极端高温作用下,轨道板底产生三处典型损伤,第一处为支承层上翘一侧,轨道板端部由轨道板和宽窄接缝挤压作用下产生的受压损伤,此处损伤相对最严重;第二处为斜裂缝上方受支承层上翘产生的受压损伤,以斜裂缝纵向相对位置为界,支承层上拱端损伤相对严重;第三处为支承层上拱端,离斜裂缝纵向相对位置约2 m处,轨道板底受压损伤,此处损伤最轻。在轨道板横向,轨道板底呈现受压损伤向板中逐渐增大的共性。在轨道板纵向,随斜裂缝纵向相对位置向板中靠近,轨道板底受压损伤逐渐增大。轨道板受压损伤受斜裂缝纵向相对位置影响不大,均表现为与宽窄接缝接触面截面突变处撕裂损伤。因此需注意斜裂贯通缝发生在板中时的轨道板伤损。

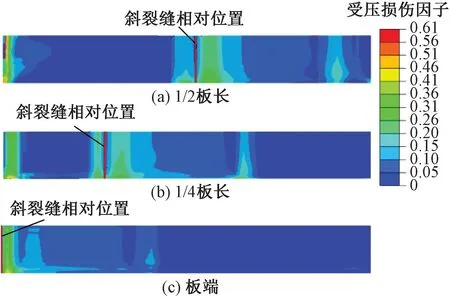
图14 轨道板底受压损伤云图

宽窄接缝损伤云图见图15。由图15可知,在极端高温作用下,宽窄接缝拉压损伤均随斜裂缝纵向位置向板端靠近而逐渐增大。当斜裂缝纵向相对位置位于板端即宽窄接缝下方时,宽窄接缝底部受支承层挤压产生严重的受压损伤,同时,宽窄接缝表面也产生次于底部的受压破坏。当斜裂缝纵向相对位置向板中靠近时,宽窄接缝底部受压损伤减小,宽窄接缝整体表现为表面损伤比底部损伤严重。支承层斜裂缝诱发的结构上拱变形,使宽接缝与窄接缝在截面突变处产生受压损伤。随斜裂缝纵向相对位置向板端靠近,宽窄接缝向轨道上拱变形的拱顶靠近,宽窄接缝竖向变形增大,宽接缝与窄接缝截面突变处撕拉作用增大,因此受压损伤逐渐增大。因此,需注意斜裂贯通缝发生在板端时的宽窄接缝伤损。

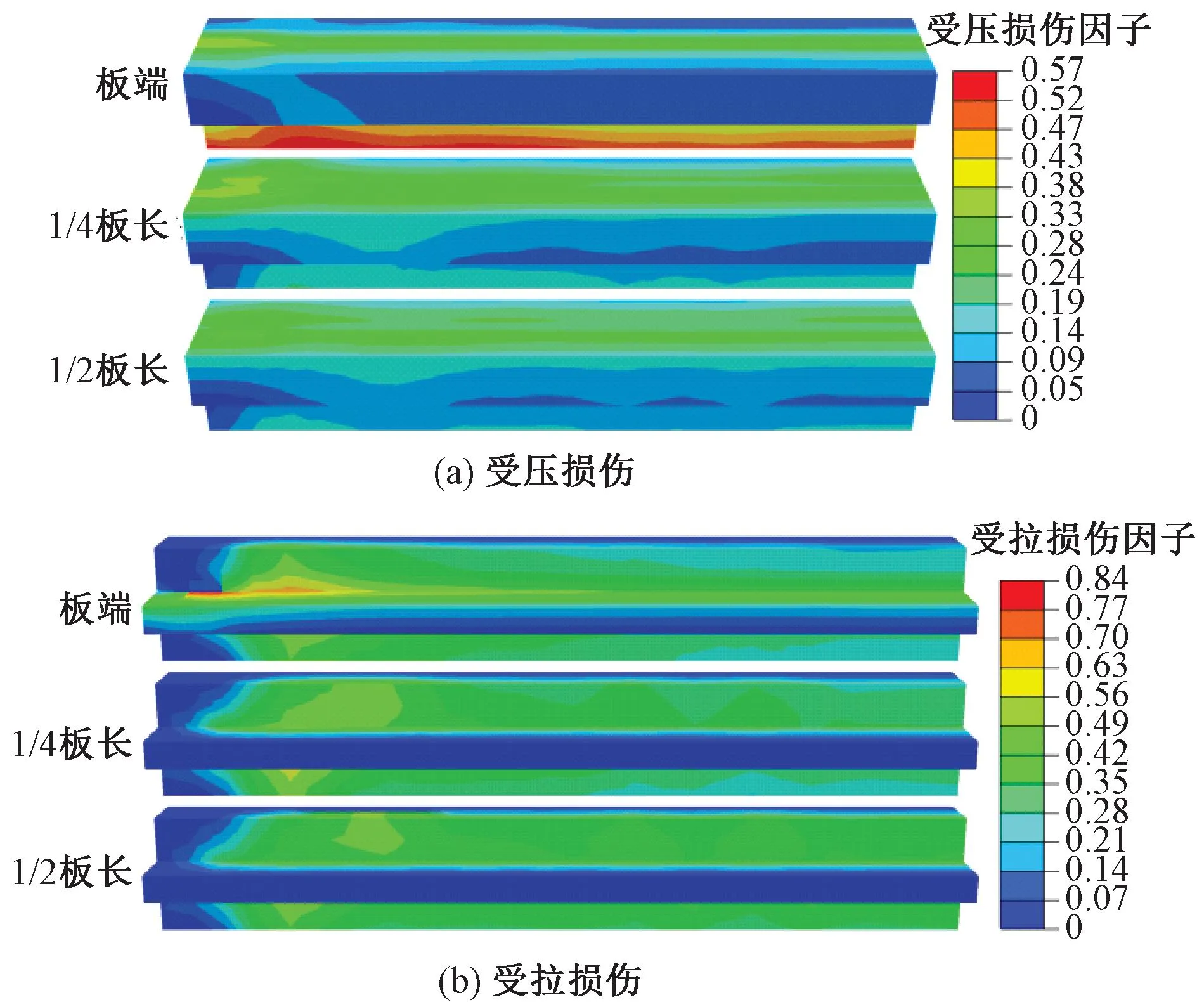
图15 宽窄接缝损伤云图

2.4 斜裂缝角度影响

在极端高温作用下,斜裂缝纵向相对位置处于跨中时,轨道结构变形随斜裂贯通缝起裂角度变化规律见图16(a)。当起裂角度为90°、60°、45°、30°、15°时,轨道结构纵向变形分别为0.8、12.5、24.3、26.5、26.0 mm。当贯通裂缝角度为90°时,轨道结构变形幅值小,斜裂缝上方的轨道板和支承层上翘端的宽窄接缝均产生较小的上拱变形。因此对比竖向贯通缝,现场检查需格外注意支承层斜裂缝的出现。当斜裂贯通缝起裂角度在45°～90°之间时,轨道结构变形随起裂角度减小急剧增大。当斜裂贯通缝在0°～45°之间时,轨道结构变形随起裂角度变化较小,结构变形随角度减小先缓慢增大随后略微减小,变化幅值不超过3 mm。

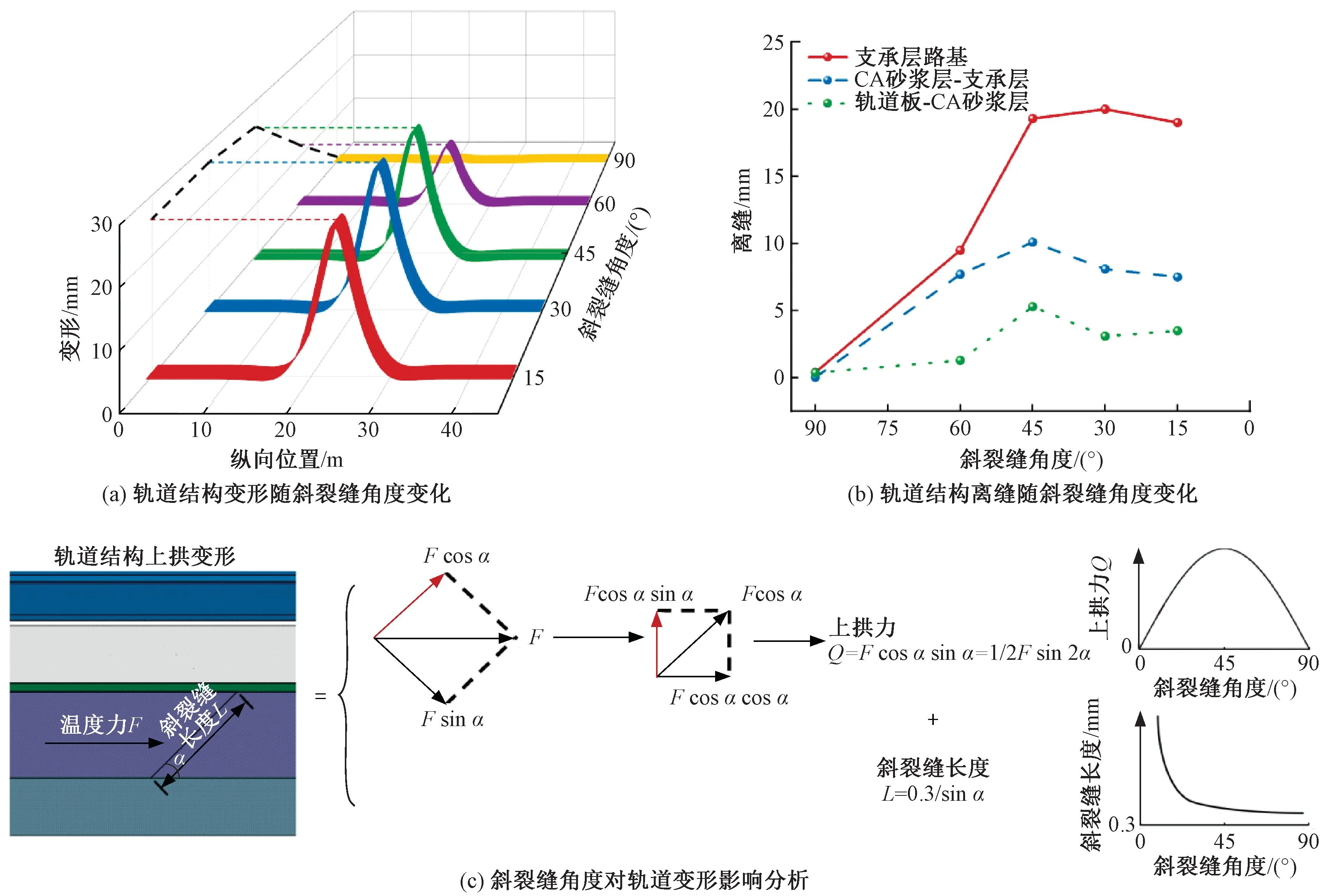
图16 斜裂缝角度对轨道结构影响

轨道结构离缝随贯通斜裂缝起裂角度的变化见图16(b),支承层与路基离缝变化规律与轨道上拱变形规律一致,当起裂角度为30°时,支承层与路基离缝达到最大值20.0 mm,CA砂浆层与支承层离缝随角度变化趋势与轨道上拱变形一致,但在起裂角度为45°时达到最大值10.1 mm,轨道板与CA砂浆层离缝在45°～90°之间与轨道上拱趋势一致,45°时达到最大值5.3 mm。在0°～45°之间,轨道板与CA砂浆层离缝随角度减小先降低后缓慢回升。由此可见,在极端高温下,支承层斜裂贯通缝诱发的纵连板最大上拱变形可达26.5 mm,支承层与路基最大离缝值可达20.0 mm,CA砂浆层与支承层离缝最大可达10.1 mm,轨道板与CA砂浆层离缝最大可达5.3 mm,且变形离缝最大值多发生在起裂角度不大于45°时。

斜裂缝角度对轨道变形的影响见图16(c)。由图16(c)可知,斜裂贯通缝角度对轨道结构的影响,主要取决于温度压力在支承层斜截面产生的上拱分力大小和斜裂缝长度所代表的支承层伤损面积。当斜裂贯通缝角度大于45°时,上拱分力随角度减小而增大,斜裂缝长度随角度减小而增大。两者效应叠加,当斜裂贯通缝起裂角度在45°～90°之间时,轨道结构变形与离缝随起裂角度减小急剧增大。当斜裂贯通缝角度小于45°时,上拱分力随角度减小而减小,斜裂缝长度随角度减小而增大。两者作用效应相反,导致当斜裂贯通缝在0°～45°之间时,轨道结构变形与离缝变化无法形成一致规律,轨道结构变形与离缝最大值多发生在起裂角度为30°或45°时。因此,现场检查需注意角度不大于45°的斜裂缝。

3 结论

本文结合内聚力理论和混凝土塑性损伤理论建立了CRTSⅡ型板式无砟轨道精细化有限元模型,对夏季高温作用下,温度、斜裂缝位置、斜裂缝角度、斜裂缝高度影响下的轨道结构的变形、离缝、受力和伤损规律进行了研究,得到以下结论:

1)随温度升高,轨道结构变形离缝规律为支承层斜裂贯通缝相互错动诱发CA砂浆层和支承层撕裂,支承层与路基离缝、支承层相互错动、CA砂浆层与支承层离缝随温度升高同时出现,随温度进一步升高,轨道板与CA砂浆层离缝随后出现,轨道结构上拱变形。

2)0～20 ℃时,轨道结构处于弹性阶段,结构变形离缝较小;20～30 ℃,结构相继进入塑性阶段,结构变形离缝加速发展;大于30 ℃时,结构变形离缝飞速发展,轨道结构塑性破坏。支承层斜裂贯通缝诱发的轨道结构变形与伤损可分为0～20 ℃的缓慢发展阶段、20～30 ℃的加速发展阶段和大于30 ℃的飞速破坏阶段。

3)随斜裂缝纵向相对位置向板中靠近,轨道结构变形增大。当斜裂贯通缝起裂角度在45°～90°之间时,轨道结构变形随起裂角度减小急剧增大。当斜裂贯通缝在0°～45°之间时,轨道结构变形随角度减小先缓慢增大随后略微减小。斜裂缝一旦贯通,轨道结构变形急剧增大。

4)当斜裂缝纵向相对位置向板中靠近,轨道板损伤增大;当斜裂缝纵向相对位置向板端靠近,宽窄接缝损伤增大。夏季高温作用下,支承层斜裂贯通缝诱发的轨道结构上拱导致轨道板和宽窄接缝底部挤压损伤、轨道板和宽窄接缝界面压溃以及轨道板和宽窄接缝横向截面突变处撕裂损伤。

5)支承层斜裂缝一旦贯通,将改变轨道上部结构纵连受力状态,极端高温作用下,轨道结构最大变形可达26 mm,支承层与路基最大离缝值可达20 mm,CA砂浆层与支承层离缝最大可达10 mm,轨道板与CA砂浆层离缝最大可达5 mm。建议温度大于30 ℃时,加强对纵向相对位置靠近跨中、角度不大于45°斜裂贯通缝的检查维修。

为研究夏季高温下支承层斜裂缝诱发的纵连板上拱规律,本文目前围绕温度和斜裂缝破损程度、位置、角度进行了相关理论研究,下一步计划开展室内模型试验验证研究。