小半径曲线地段无砟轨道钢轨碎弯影响因素分析

许晨霄，李怡涵，袁 帅，程卓亮，李一悦

(中国铁路西安局集团有限公司西安工务段，陕西 西安 710000)

利用“统一公式”和“不等波长公式”等方法检算有砟轨道横向稳定性已较为成熟，而对于无砟轨道，由于无砟轨道的扣件系统与轨道板直接连接，相比有砟轨道，无砟轨道整体性强、保持轨道几何形位的能力强，其无缝线路稳定性相对更好[1]。但近年来一些研究调查表明，在钢轨纵向力、钢轨初始弯曲、线路横向抗力等作用下，无砟轨道无缝线路的钢轨可能以碎弯的形式产生一定的横向变形，容易致使车辆出现蛇行运动，严重情况下危害行车安全，加速钢轨碎弯地段磨耗损伤，引起无缝线路静、动力学指标超限[2-4]。因此，无砟轨道无缝线路稳定性问题的研究是不容回避的，这也是带给无缝线路技术的新问题。目前，一些学者对无砟轨道无缝线路钢轨碎弯变形展开了一定程度的研究[5-7]，而现有研究关于无砟轨道钢轨碎弯的研究相对较少，且主要集中在直线地段，还无针对小半径曲线地段钢轨碎弯变形的研究。本文针对大跨度连续梁桥，以单元板式轨道与钢弹簧浮置板轨道为研究对象，分别分析了小半径曲线地段钢轨初始弯曲、曲线半径、扣件整体横向刚度、钢弹簧整体横向刚度对钢轨碎弯变形的影响及作用规律。

1 模型的建立

1.1 模型概述

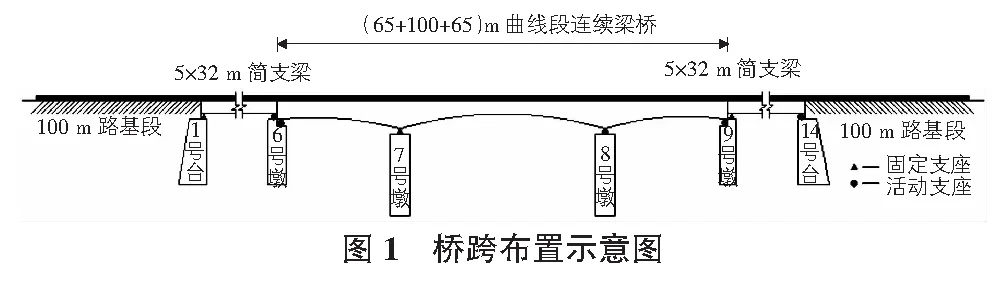
基于梁-板-轨相互作用理论，利用有限元ANSYS建立小半径曲线地段桥上单元板式轨道和钢弹簧浮置板轨道计算模型，曲线段两端为5跨32 m长的直线简支梁桥和100 m路基段，以消除边界效应，桥跨布置示意图见图1。

1.2 计算参数

桥梁梁体、底座板、轨道板、扣件系统和钢轨为桥上单元板式轨道的主要组成部分，钢轨采用60轨，扣件采用WJ-14型常阻力扣件，其最大纵向阻力为10 kN，横向和垂向刚度为50 kN/mm,35 kN/mm；参考文献[8]，钢弹簧纵向刚度与横向刚度取为75.6 kN/cm，垂向刚度为63 kN/cm，混凝土强度等级为C50；参考《铁路轨道设计规范》和文献[9]，桥台纵向、横向刚度均取3 000 kN/cm，连续梁均取4 000 kN/cm，简支梁均取500 kN/cm，所建立的计算模型见图2。

2 钢轨初始弯曲的影响

随着我国轨道交通的快速发展，轨道交通中长大跨度连续梁桥的应用也越来越广泛，无缝线路梁轨相互作用使得钢轨纵向力进一步增加。同时，根据一些研究显示[10-12]，运营之后的线路普遍存在3 ℃～10 ℃锁定轨温的下降，致使钢轨纵向力更大，出现钢轨碎弯的可能进一步增大。综合考虑出现钢轨碎弯的不利因素，参考《铁路无缝线路设计规范》和《铁路轨道设计规范》，桥梁取年温差30 ℃；考虑轨道板受气温变化影响较大，其温差一般不小于混凝土桥梁的温差，故轨道板和底座板温差取30 ℃；同时，考虑钢轨温升时最大温差33.7 ℃和锁定轨温下降5 ℃，即钢轨温升时的温度荷载取38.7 ℃。

2.1 碎弯变形分析

当线路存在钢轨初始弯曲，温升时钢轨在较大纵向压力的作用下，积聚在钢轨内部的温度力会向着势能低处发生能量转移，轨条在有初始弯曲的区段可能发生臌曲变形。由于轨道板和扣件阻力的约束作用，这种臌曲变形不会发展到轨条失稳，只可能始终处于胀轨状态，从而形成碎弯。新轨对初始弯曲有严格的要求，但限于生产工艺、运输、铺设等多方面的原因，钢轨发生弹性或塑性初始弯曲是一种无法完全避免的客观存在。

钢轨初始弹性弯曲为正弦曲线，可用式(1)表示：

(1)

其中，yo为钢轨初始弹性弯曲函数；fo为钢轨初始弹性弯曲矢度,cm；l0为钢轨初始弯曲半波长,cm。

本节讨论小半径曲线地段单元板式轨道和钢弹簧浮置板轨道在不同波幅-波长组合下有着初始弹性弯曲波形的钢轨，在温度荷载作用下的横向变形情况，曲线半径取400 m。初始弯曲波幅分别取1 mm,2 mm,4 mm和8 mm，初始不平顺波长分别取0.5 mm,0.7 mm,0.9 mm,1.2 mm,1.5 mm,…,9.0 mm，计算得出波长-波幅与钢轨最大横向变形的关系，如图3所示。

分析图3可知，对于单元板式轨道，当波幅为1 mm和2 mm时最不利波长为0.7 m，不利波长范围为0.5 m～2 m左右，而当波幅为4 mm和8 mm时最不利波长为1.2 m，不利波长范围为0.5 m～4 m左右；对于钢弹簧浮置板轨道，当波幅为1 mm，2 mm，4 mm和8 mm时最不利波长均为1.5 m，波长0.5 m～8 m范围内钢轨最大横向变形有较强波动性；单元板式轨道波幅分别为1 mm,2 mm,4 mm 和8 mm时最不利波长对应的横向变形最大值分别为10.27 mm，10.30 mm，10.38 mm，10.54 mm，波幅从1 mm 增至8 mm时最不利横向变形最大值增幅为2.56%，钢弹簧浮置板轨道波幅分别为1 mm,2 mm,4 mm和8 mm时最不利波长对应的横向变形最大值分别为11.81 mm，11.89 mm，12.04 mm，12.32 mm，增幅为4.32%；与单元板式轨道相比，浮置板轨道横向变形最大值相对较大，波幅分别为1 mm,2 mm,4 mm和8 mm时最不利波长对应的横向变形最大值分别相差15.00%,15.44%,15.99%,16.89%。当波长到达最不利波长位置之后，随着波长的增大，横向变形最大值的波动性随之逐渐降低，对于单元板式轨道，当波长超过6.3 m后趋于稳定，对于钢弹簧浮置板轨道，当波长超过9 m左右后钢轨最大横向变形才趋于稳定；当波长一定时，钢轨横向变形最大值的波动性随波幅的增大而增大。

2.2 轨向偏差

经计算分析，不同波幅-波长组合下有着初始弹性弯曲变形的钢轨，在温度荷载作用下轨距偏差基本不变，而轨向偏差较大，计算得出波长-波幅与钢轨最大轨向偏差的关系，如图4所示。

分析图4可知，对于单元板式轨道，当波幅为1 mm,2 mm和4 mm时最不利波长均为0.7 m，波幅8 mm时波长1.5 m处的轨向偏差最不利，不利波长范围为0.5 m～4 m左右，而对于钢弹簧浮置板轨道，最不利波长均为5.1 m，不利波长范围为0.5 m～8 m左右；单元板式轨道波幅分别为1 mm,2 mm,4 mm和8 mm时最不利波长对应的轨向偏差最大值分别为2.70 mm，2.74 mm，2.84 mm，3.01 mm，波幅从1 mm增至8 mm时轨向偏差最大值增幅为11.48%，钢弹簧浮置板轨道最不利波长对应的轨向偏差最大值分别为2.85 mm，2.94 mm，3.10 mm，3.45 mm，增幅为21.05%；与单元板式轨道相比，浮置板轨道轨向偏差最大值相对较大，波幅分别为1 mm，2 mm，4 mm和8 mm时最不利波长对应的轨向偏差最大值分别相差5.56%，7.30%，9.15%，14.62%。

3 曲线半径的影响

本节主要分析不同曲线半径对钢轨碎弯变形、轨向偏差的影响，同时考虑不同曲线半径下不同波长区段钢轨初始弯曲对横向变形和轨向偏差的作用，取波幅f=4 mm，得出不同曲线半径下钢轨横向变形和轨向偏差的最大值，如图5所示。

分析图5可知，当曲线半径从400 m增大至1 200 m时，钢轨横向变形最大值从10.38 mm减小到4.34 mm，减小了6.04 mm，降幅为58.19%，轨向偏差最大值从2.84 mm减小到1.14 mm，减小了1.70 mm，降幅为59.86%。

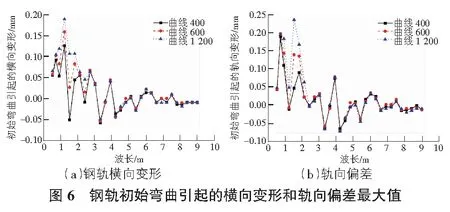
经计算分析，仅温度荷载作用下，曲线半径400 m，600 m和1 200 m下钢轨横向变形的最大值分别为10.25 mm，7.26 mm，4.16 mm，轨向偏差的最大值分别为2.65 mm,1.79 mm,0.91 mm，钢轨初始弯曲引起的横向变形和轨向偏差最大值可由初始弯曲+温度荷载作用下的最大值减去仅温度荷载作用下的最大值得到，如图6所示。分析图6可知，曲线半径400 m,600 m和1 200 m下钢轨初始弯曲引起的横向变形最大值最不利波长均为1.2 m，曲线半径主要影响波长0.5 m～2.4 m范围内的横向变形，超出波长2.7 m后钢轨初始弯曲引起的横向变形基本不变；曲线半径400 m,600 m下初始弯曲引起的轨向偏差最不利波长为0.7 m，而曲线半径1 200 m下最不利波长为1.5 m，曲线半径主要影响波长0.7 m～2.1 m 范围内的轨向偏差，超出波长2.4 m后初始弯曲引起的轨向偏差基本不变。

4 横向刚度的影响

4.1 扣件横向刚度

本节主要分析不同扣件横向刚度对钢轨碎弯变形和轨向偏差的影响，曲线半径取400 m，取波幅f=4 mm，扣件横向刚度从10 kN/mm～80 kN/mm进行取值，当计算钢轨横向变形时取最不利波长L=1.2 m，当计算轨向偏差时取最不利波长L=0.7 m，图7为扣件横向刚度与钢轨横向变形、轨向偏差的关系。

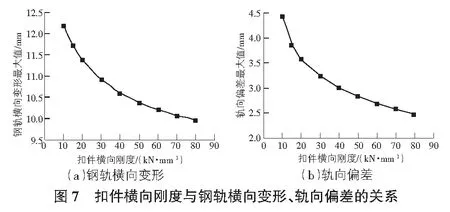
分析图7可知，钢轨横向变形与轨向偏差的最大值随扣件横向刚度的增大而逐渐减小，当扣件横向刚度从10 kN/mm增大至40 kN/mm时，钢轨横向变形最大值从12.20 mm减小至10.60 mm，减小了1.60 mm，降幅为13.11%，轨向偏差最大值从4.42 mm减小至3.01 mm，减小了1.41 mm，降幅为31.90%；当扣件横向刚度从50 kN/mm增大至80 kN/mm时，钢轨横向变形最大值从10.38 mm减小至9.97 mm，减小了0.41 mm，降幅为3.95%，轨向偏差最大值从2.84 mm减小至2.49 mm，减小了0.35 mm，降幅为12.32%；当扣件横向刚度超出50 kN/mm左右后对钢轨横向变形和轨向偏差的影响较小，且过大的扣件横向刚度会加速扣件疲劳损伤；若初始扣件横向刚度为50 kN/mm，当扣件横向刚度损失超过40%时，钢轨横向变形和轨向偏差将显著增加，当扣件横向刚度损失超过70%左右时，轨向偏差将超出限值4 mm。

4.2 钢弹簧横向刚度

本节主要分析不同钢弹簧横向刚度对钢轨碎弯变形和轨向偏差的影响，同4.1节，曲线半径取400 m，取波幅f=4 mm，钢弹簧横向刚度从10 kN/cm到120 kN/cm进行取值，当计算钢轨横向变形时取最不利波长L=1.5 m，当计算轨向偏差时取最不利波长L=5.1 m，图8为钢弹簧横向刚度与钢轨横向变形、轨向偏差的关系。

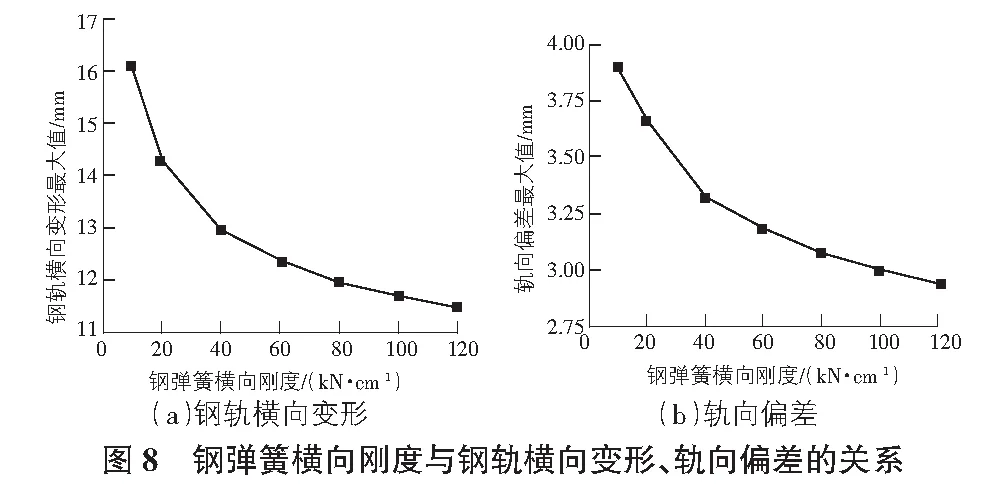
分析图8可知，钢轨横向变形与轨向偏差的最大值随钢弹簧横向刚度的增大而逐渐减小，当钢弹簧横向刚度从20 kN/cm增大至60 kN/cm时，钢轨横向变形最大值从14.26 mm减小至12.36 mm，减小了1.90 mm，降幅为13.32%，轨向偏差最大值从3.66 mm减小至3.19 mm，减小了0.47 mm，降幅为12.84%；当钢弹簧横向刚度从80 kN/cm增大至120 kN/cm时，钢轨横向变形最大值从11.97 mm减小至11.49 mm，减小了0.48 mm，降幅为4.01%，轨向偏差最大值从3.08 mm减小至2.94 mm，减小了0.14 mm，降幅为4.55%；当钢弹簧横向刚度超出80 kN/cm左右后对钢轨横向变形和轨向偏差的影响较小，若初始钢弹簧横向刚度为80 kN/cm，当钢弹簧横向刚度损失超过50%时，钢轨横向变形和轨向偏差将显著增加。

5 结语

1)在不同波长-波幅组合下，钢轨横向变形最大值与轨向偏差最大值最不利波长与不利波长范围各有不同，最不利波长对应的钢轨横向变形与轨向偏差随波幅的增大而增大；2)当曲线半径从400 m增大至1 200 m时，钢轨横向变形和轨向偏差的最大值分别减小了58.19%，59.86%，曲线半径主要影响波长0.5 m～2.4 m范围内的横向变形，主要影响波长0.7 m～2.1 m范围内的轨向偏差；3)钢轨横向变形与轨向偏差的最大值均随扣件整体横向刚度、钢弹簧整体横向刚度的增大而逐渐减小，当扣件横向刚度和钢弹簧横向刚度分别超出50 kN/mm,80 kN/cm左右后对钢轨横向变形和轨向偏差的影响较小；4)若初始扣件横向刚度为50 kN/mm，当刚度损失超过40%时钢轨横向变形和轨向偏差将显著增加，当刚度损失超过70%左右时轨向偏差将超出限值4 mm；若初始钢弹簧横向刚度为80 kN/cm，当刚度损失超过50%时钢轨横向变形和轨向偏差将显著增加。