自驱旋转式能量回收装置的转速特性曲线

杨大壮,袁丹青,李辉

(江苏大学能源与动力工程学院,江苏 镇江 212013)

海水淡化技术从20世纪50年代开始了大规模开发使用,其通过开源的方式增加淡水总量,且不受空间和时间的限制,这对于中国沿海城市和岛屿生产生活有着重要的战略意义[1].其中反渗透海水淡化技术凭借其处理水质好、节能和可复制性强的优势而迅速占领了市场,而且正以每年10%以上的速度增加[2-4].

在反渗透海水淡化系统(seawater reverse osmosis system)多种能量回收装置中,自驱旋转式能量回收装置(self-driving rotary energy recovery device,SDRERD)因其稳定、高效的特性,在一众能量回收技术中脱颖而出.但自驱旋转式能量回收装置专利技术一直牢牢把控在以ERI公司为代表的西方发达国家企业的手中,且价格高昂.在国际竞争日益激烈与全球淡水资源紧缺今天,自驱旋转式能量回收装置的国产化进程对中国海水淡化工程的战略安全有非常积极的意义.

反渗透海水淡化技术是利用半渗透膜的渗透压原理来达到水分子与离子分离的目的,图1为反渗透海水淡化技术的工艺流程图.反渗透海水淡化技术相比于其他技术路线最明显的优势就是能耗低,而降低反渗透海水淡化技术能耗的关键设备就是高效的能量回收装置,其中以基于正位移原理的自驱旋转式能量回收装置回收效率最高,达到了92%以上[5-6].

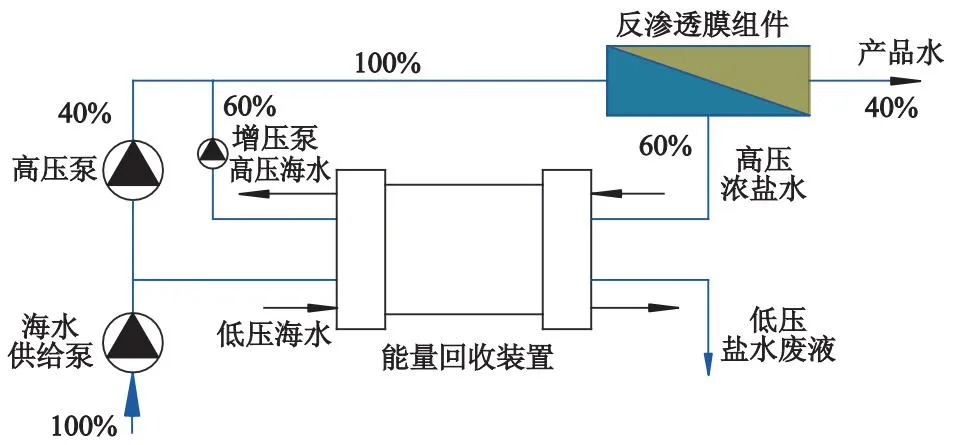
图1 反渗透技术工艺流程

自驱式能量回收装置的主要部件:带有周向均匀布置贯通孔道的转子;与转子间隙配合的套筒;上下2个分别带有2个集液盘的端盖.自驱式能量回收装置核心部件的制作材料均为高纯度氧化铝陶瓷,如图2所示.

图2 自驱式能量回收装置结构示意图

液体经过进口流道进入集液盘,并在集液盘内减速升压后进入轴向孔道,进入前的流体速度矢量与转子端面形成了一定的夹角θ,如图3所示,进而产生了切向速度,该切向速度分量可驱动固体转子转动.

图3 集液盘与内外层转子孔道配合关系

BROSS等[7]设计了一种外表面有螺旋槽的转子结构,可以实现转子的自启动旋转,并根据流量的变化调整转子转速.韩松等[8]采用流固耦合的方法分析了转子转速的变化规律.XU等[9]等提出一种理论计算方法,用于计算转子动力矩和阻力矩,进而结合边界条件计算出自驱式能量回收装置的转速特性曲线.PIQUE等[10]通过对PX装置进行试验,发现液压自驱动能量回收装置的转子转速与装置的流量和集流盘的倾斜角有关,但没有给出确定转速的方法.MARTIN等[11]采用工业陶瓷作为关键部件,优化了转子内通道,使转子由覆盖整个端面的多列圆形通道组成.

文中基于Fluent 6DOF模型,结合理论分析的方法,建立相应的数学模型与数值分析模型,以实现刚体转子的被动旋转,并对装置转子转速特性进行研究分析.

1 转子转速特性理论

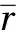
根据装置进口流量Q与面积A,可以求得进口流道的平均轴流速度Vy为

(1)

由于流体要通过集液盘减速增压后进入转子孔道,为了求得转子转速,须先求得集液盘与转子交界面处的平均轴流速度Vy′,即

(2)

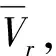
(3)

由于转子驱动力来源于转子转速与流体切向速度之间的速度差[12-14],则当两速度相等时,转子达到稳定转速,即达到额定转速,计算式为

(4)

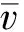
将能量回收装置有关结构参数和式(3)代入式(4),得到转子转速N与驱动流体在交界面处的平均切向速度的函数关系,即

(5)

图4为理论转速特性曲线图,由图可以看出,在没有进流流体驱动时,转子转速为0;随着进口流量增大,转子转速亦增大,即两者成正比.

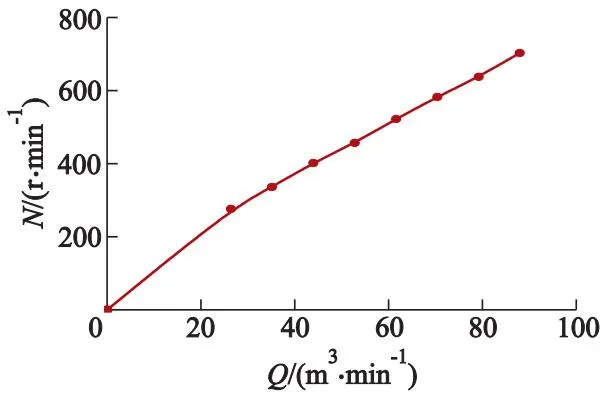
图4 理论转速特性曲线

2 数值模拟方法

2.1 计算模型及网格划分

应用ICEM 19.0对全流道采用六面体结构化网格进行划分.为了更好地捕捉靠近壁面处的流动,沿液膜方向取10层网格,Y+控制在30～100.经网格无关性验证后,整体网格数增加到280万左右,转子网格质量控制在0.6以上.图5为流场网格划分图.

图5 流场网格划分

2.2 UDF编码

6DOF模型的UDF编译文件如下:

#include"udf.h"

DEFINE_SDOF_PROPERTIES(rotaotr,prop,dt,time,dtime)

{

prop[SDOF_MASS]=7.282;

prop[SDOF_IXX]=3.9940e-002;

prop[SDOF_IYY]=3.5783e-002;

prop[SDOF_IZZ]=3.9942e-002;

prop[SDOF_ZERO_ROT_X]=TRUE;

prop[SDOF_ZERO_ROT_Z]=TRUE;

prop[SDOF_ZERO_TRANS_X]=TRUE;

prop[SDOF_ZERO_TRANS_Y]=TRUE;

prop[SDOF_ZERO_TRANS_Z]=TRUE;

}

上述代码物理含义为转子质量7.282 kg;X,Y,Z方向的转动惯量分别为3.994 0×10-2,3.578 3×10-2, 3.994 2×10-2kg/m2;并抑制X和Z方向上的转动,以及X,Y和Z方向上的滑动,且不抑制Y方向的转动.

2.3 边界条件设置

文中侧重于对转速特性的分析,故统一设置介质为清水以简化运算步骤.设置高压、低压进口为速度进口(velocity inlet);设置高压、低压出口为压力出口(pressure outlet),分别为6.0,0.2 MPa.定子端盖与转子孔道水体接触面设置为交界面(interface).计算时选择双精度,收敛精度设为1.0×10-4,离散格式采用二阶迎风格式.

3 计算结果分析

以装置进口流量Q为70.2 m3/h,装置出口压力p为6.0 MPa的工况为例.转子启动过程中不同时刻t1的速度分布如图6所示.

图6 速度分布

图6中时刻0.2 s时,转子孔道由左向右分别为1,2,3,4,5,6号孔道,1—6号转子孔道统称为能量交换区.与集液盘完全没有接触的转子孔道称为密封区.如无特殊说明,后续分析中各时刻转子孔道分布不变.

由图6可知:时刻0.2 s时,定子进口集液盘内流体速度呈均匀分布,2—5号转子孔道内壁面处流体速度依次减小.由于存在θ,5号转子孔道接收的经集液盘减速增压后流体的切向速度较小,而2号转子孔道处的θ较小,所以流体的切向速度较大.

时刻0.5 s时,转子进一步吸收流体动能,2—4号转子孔道内部流体流速分布趋同,且孔道内的速度相比于0.2 s时明显减小,并与5号转子孔道流体流速分布差异明显.

此时5号转子孔道流体流速显著低于集液盘内流体流速,在能量交换区形成了低速区,低速区会对固体转子产生一定的负扭矩.

时刻0.8 s时,5和6号转子孔道均出现大片低速区,此处流体速度矢量大幅转向,进而阻碍流体进入转子孔道,此时低速区引起的负扭矩对转子的加速过程产生了严重的阻碍.

从图6的速度分布还可以看出:不同位置的流体切向速度对转子转速的影响各不相同,由低速区带来的负扭矩与高速区带来的正扭矩相互抵消,进而使得装置转子在忽略间隙流动的摩擦阻力下仍能够在一定的转速下稳定运行,而不会在数值模拟计算时因缺少摩擦阻力导致转子一直处于加速状态,使得数值模拟结果与工程实践之间存在巨大的偏差.

图6的整个过程中,由于1号和6号转子孔道与集液盘未完全接触,转子孔道处于过渡阶段,导致流体不能顺利进入转子孔道,所以孔道内部流体流动失稳,因此1号和6号转子孔道流体流速均较小,且速度分布较为混乱.

与能量交换区不同的是,各时间点下的转子密封区内流体速度分布极为均匀,且速度接近于0.转子密封区的流体经传递压力能后,由高压流体转化为低压流体,且与上、下集液盘均无接触,处于密封状态,所以速度极小.

对比图6各时间点左右两图的流体速度分布,发现同一时刻高压交换区与低压交换区的流体速度分布极为相似,这说明在同等进口流量下,高、低压流体对转子的驱动效果相似.

图7为各工况下0～5 s内装置转子所受扭矩M随时间t变化图.由图可知:不同工况下转子所受扭矩随时间的变化均呈现同一个规律,即一定时间内扭矩随时间增大而减小,在扭矩第1次归0后,再到一定负值,然后沿M为0坐标轴上下波动.

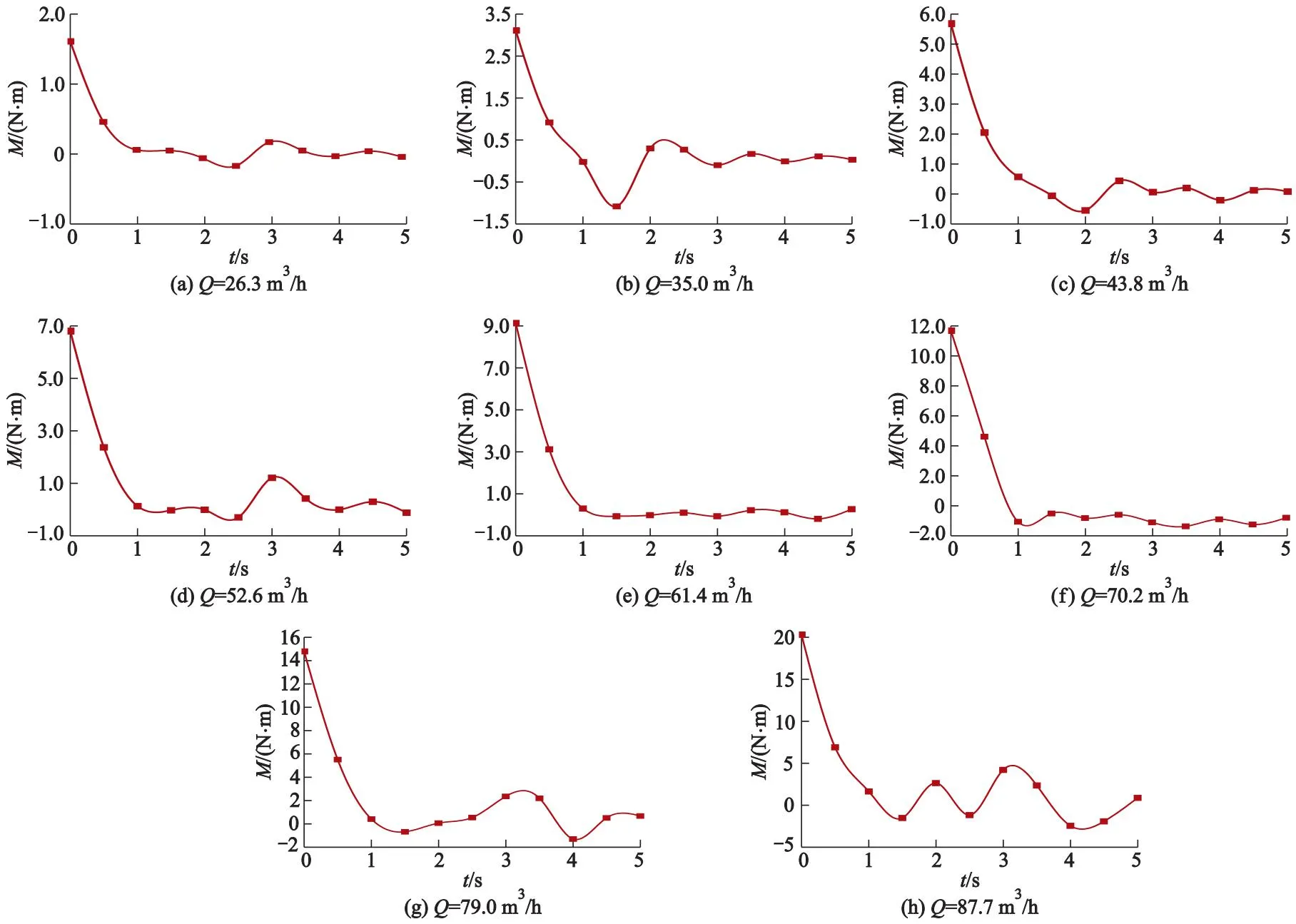
图7 不同工况转子所受扭矩随时间变化

结合图7中3种工况26.3,70.2,87.7 m3/h下转子所受扭矩可得:小流量工况下由于进口初速小,集液盘内平均切向速度较小,所以其启动时间长于较大流量的启动时间;另一方面流量大于70.2 m3/h后,即使流量增大引起进口初速增大,在工况87.7 m3/h下转子的启动时间为1.2 s,并且工况87.7 m3/h下扭矩在初次达到零点后的振幅并未随时间增大而减小,反而愈发不稳定.

同时由图7中各工况在时刻0 s的最大扭矩可知:转子的驱动扭矩随流量增加而增大,即驱动扭矩与流量成正比.这表明了装置流量是转子启动时间和最终转速的重要影响参数.

图8为各工况下转子扭矩初次归0时间图,即启动时间随流量的变化图.由图可知:转子在工况70.2 m3/h下归0所耗时间最短,即转子启动时间最短.

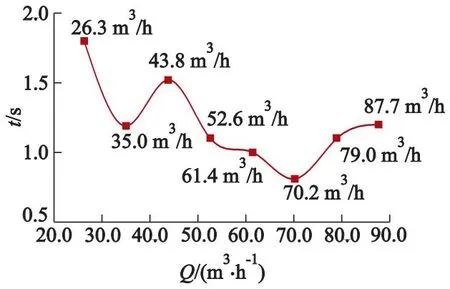
图8 各工况转子扭矩初次归0时间

工程实践中,自驱旋转式能量回收装置通常要配合相应的监测与控制系统,以保证反渗透海水淡化系统的运行安全.为方便后续工作,取在相同操作压力下装置转子扭矩初次归0时间最短,且满足扭矩初次归0后随时间的增加而沿M为0坐标轴上下震荡、振幅不断减小直到振幅稳定在一定区间内2个条件的流量为装置额定流量,其物理含义为自驱旋转式能量回收装置在保证稳定运行下能够承载的最大流量,且取在稳定运行期间转速的平均值为此额定流量下的额定转速.故文中所研究装置的额定流量为70.2 m3/h,此额定流量下的额定转速为580 r/min.

图9为基于Fluent 6DOF模型确定的各工况下转速特性曲线图.由图可知:转子的转速随流量的增大而增大,且各条转速特性曲线斜率随流量的增大而增大,即转子启动时的加速度也与流量成正比.

图9 各工况下转速特性曲线

图10为理论分析与数值模拟分别预测的各工况下转子转速特性曲线.从图中可以得出:小流量工况26.3 m3/h下的相对误差最高,达14.9%,其原因是转子转速绝对值较小;工况61.4 m3/h下的相对误差最小,为0.77%.数值模拟数据与理论分析数据吻合度较高,表明数值模拟计算的结果有一定的可靠性.

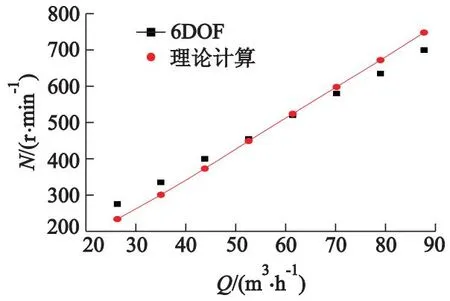
图10 转子转速特性曲线对比

4 结 论

1) 对自驱旋转式能量回收装置的转速特性曲线进行理论计算,根据转子驱动扭矩本质与集液盘内切向速度和转子转速线速度之差的平衡关系,推导出一种新的转速特性曲线预测模型,并得出了不同工况下转子转速特性曲线.理论转速特性曲线与模拟结果最大相对误差为14.9%,最小相对误差为0.77%.

2) 转子的额定转速与装置流量成正比;过大流量会使转子运行失稳,同时启动时间长于装置额定工况的启动时间.在低于额定流量的工况下,转子的启动时间与装置流量成反比,大于额定流量的工况下转子的启动时间与装置流量成正比.

3) 转子具有良好的转速自适应性.忽略转子端面间隙与环面间隙形成的阻力矩对转子额定转速的影响,转子转速仍能稳定在某一额定区间.