导叶安装角度对离心泵叶轮结构特性的影响

裴吉,刘总帅,王文杰,韩振华

(江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)

带导叶蜗壳式离心泵是广泛应用于大型调水工程中的重要设备,由于其运行时叶轮高速旋转所产生的水压力交变载荷对叶轮结构强烈冲击,会引发机组的振动,甚至可能导致其发生破坏,影响泵装置的正常运行[1-2],因此,为提高大型蜗壳式离心泵的运行稳定性,对其进行结构特性分析是必要的.

目前,国内外已有学者采用流固耦合方法对结构的变形与等效应力进行分析,并通过模态分析其振型等[3-6].刘厚林等[7]分别采用顺序耦合和双向流固耦合方法对导叶式离心泵进行强度分析,表明顺序耦合和双向耦合的结果基本一致.KAN等[8-9]采用流固耦合方法先研究了延伸轴贯流泵叶片应力分布及变化规律,之后对轴流泵叶片提出了一种降低其根部附近应力集中的方法,该方法可有效减小叶片不可靠区域出现裂纹的可能性.陈小翠等[10]考虑不同工况及不同水轮机材料,对某冷却塔水轮机转轮进行流固耦合分析和干湿模态分析,得到转轮在2种情况下的固有频率和振型,并进行试验验证.SHI等[11]采用流固耦合方法对贯流泵和轴流泵叶片的结构强度和模态特性进行了比较研究.TIAN等[12]对多级高速离心泵转子进行了模态分析,发现其干、湿2种模态下的固有频率差异明显,因此在计算过程中应考虑流固耦合对动力学特性的影响.高海司等[13]对蜗壳式混流泵叶轮部件进行干湿模态对比分析,并考虑不同材料属性以及加大叶轮前后盖板厚度等影响,结果表明,加大后盖板厚度对提高各阶固有频率最明显.侯旋[14]针对双螺杆压缩机转子提出了一种基于双向计算流体动力学(CFD)/计算结构动力学(CSD)的流固耦合计算方法,对单、双向流固耦合下双螺杆压缩机螺杆结构的强度及振动特性进行了研究.吴港永等[15]对液环泵转子部件进行流固耦合分析,研究了叶轮叶片的应力及变形量分布特征、旋转角引起的非稳态特性以及转子部件的模态特性等.

虽然流固耦合方法在流体机械领域应用广泛,但是对于大型带导叶蜗壳式离心泵,导叶安装角度变化对其性能以及叶轮结构力学响应的影响并不明确.文中基于ANSYS Workbench平台,首先对4种不同导叶安装角度的蜗壳泵流场进行数值计算,得到其外特性曲线;再利用单向流固耦合,将流场计算结果的水压力载荷导入叶轮结构,计算叶轮在不同条件下的变形和等效应力变化特性;最后,研究叶轮结构在有无预应力下的干湿模态对比,分析其结构振动特性,从而为带导叶蜗壳式离心泵叶轮结构优化提供一定的参考.

1 数值计算

1.1 计算模型

以某大型带导叶立式蜗壳泵的模型泵为研究对象,该模型泵的主要设计参数分别为扬程Hd=21 m,流量Qd=920 m3/h,转速n=1 250 r/min;叶轮叶片数Zi=6,导叶数Zd=8.应用三维建模软件UG对模型泵整个水体进行实体建模,如图1所示,过流部件主要包括进水弯管、叶轮、导叶、蜗壳、出口流道等,其中出口流道长度取其管径的4倍.

图1 水体模型

在本研究模型中,导叶安装角度β是指导叶上(不含两侧圆角处)任一点的切线与此点和轴心连线的切线方向的夹角,导叶的旋转中心与轴心距离为215 mm.

先根据模型结构特性对导叶安装角β在8°～20°进行外特性数值计算,然后根据计算结果选择4种具有代表性的角度(10°,12°,14°,16°)进行分析.

1.2 网格划分及无关性验证

在过流部件的网格划分中,叶轮和导叶适用于使用TurboGrid软件进行结构网格划分,而蜗壳几何形状复杂,因此采用适应性较强的非结构四面体网格划分,进水弯管和出水流道则采用ANSYS ICEM CFD进行结构网格划分.

以导叶安装角度为16°时划分6套网格,在额定工况下,以扬程为判据,进行网格无关性验证.当网格数超过400万时,扬程变化小于1%.综合考虑计算精度和计算资源,最终选取的计算网格数约为440万,其中叶轮、导叶、蜗壳、进水弯管和出口流道的网格单元数分别为180万、80万、70万、70万、40万.

1.3 边界条件

应用ANSYS CFX软件对模型泵内流场进行数值计算,采用标准k-ε湍流模型[16].所有计算区域参考压力设置为0,进口边界条件设置为总压进口,出口给定为质量流量出口.壁面采用无滑移且光滑边界条件.定常计算时进口弯管与叶轮、叶轮与导叶的交界面设置为“Frozen Rotor”模式,非定常计算时设置为“Transient Rotor Stator”模式,其他设置为“None”.非定常计算时间步长设为0.40 ms,即叶轮旋转3°时长,总时间为0.24 s,即叶轮旋转5个周期时长.

1.4 数值计算方法可靠验证

为验证数值计算方法的可靠性,在导叶安装角度为16°时,对模型泵进行试验测试,并将试验数据与定常数值计算结果进行对比.在小流量工况下数值计算与试验的扬程误差很小,而在大流量工况下,扬程误差稍大,最大误差小于8%,表明文中所采用的数值计算方法是可靠的.

2 计算结果及分析

2.1 模型泵外特性分析

图2为4种导叶安装角度下蜗壳泵模型的扬程和效率曲线,可以看出:在小流量工况下,扬程和效率都随着导叶安装角度的增大而减小,随着流量增大,这种差距逐渐减小;在设计流量工况附近时,导叶安装角度对扬程和效率的影响最小,之后出现相反的变化规律,即在大流量工况下,β=16°,14°时模型泵性能最好,且变化幅度最小;当导叶安装角β=10°时,模型泵的扬程和效率在大流量工况下有比较明显的下降;整体看,随着导叶安装角度减小,泵的高效区向小流量工况发生偏移,并且最高效率逐渐增大,最大提高达2.1%.

图2 不同导叶安装角度下模型泵的外特性曲线

2.2 叶轮变形与应力变化分析

2.2.1 叶轮结构约束设置

采用UG软件对叶轮部件进行三维实体建模,在建模过程中对其进行简化,剔除一些对计算结果影响较小的零件或者倒圆角等.分别应用ANSYS Workbench中的Static Structural模块和Transient Structural模块进行稳态和瞬态的单向流固耦合计算,叶轮材料设置为默认结构钢,密度为7 850 kg/m3,弹性模量为200 GPa,泊松比为0.3.

对叶轮结构生成四面体网格,并对关键部位进行加密,最终获得的网格数约为28万(见图3).

图3 叶轮网格

分别添加约束条件,对叶轮定义重力方向以实现重力载荷的加载,在叶轮与轴的接触面设置为固定约束条件.分别设置叶轮叶片、前盖板、后盖板3组载荷传递面,以确保流体计算的水压力能够准确传递到叶轮上.叶轮结构载荷添加与约束布置如图4所示.

2.2.2 叶轮变形与应力变化

利用静态结构分析模块将定常计算得到的水压力加载到叶轮结构上,得到叶轮在各个条件下的最大变形量与最大等效应力值的变化规律,如图5所示,图中εmax为最大变形量,δmax为最大等效应力.

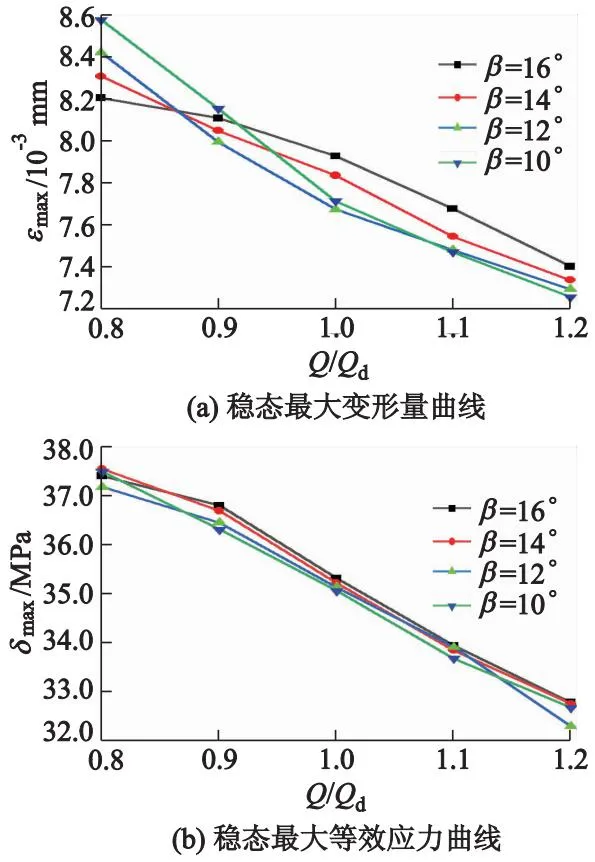
图5 稳态变形与应力变化曲线

由图5可以看出:最大变形量和最大应力值都随流量的增大而减小;对于不同导叶安装角度下的叶轮最大变形量,除β=10°外,其他均有明显变化规律,即在0.8Qd工况下随着导叶安装角度的减小而增大,在0.8Qd～0.9Qd工况下某个点差距达到最小,之后的流量工况下,都随着导叶安装角度的增大而增大,最大差值达3.3%,并且在大流量工况下,导叶安装角度对叶轮最大变形量的影响较其他工况的要小一些;导叶安装角度对最大等效应力值的影响较小,但在设计流量工况附近依旧遵循随着导叶安装角度的减小而减小的规律,在0.8Qd和1.2Qd工况下,β=16°,14°,10°时对最大等效应力值的影响达到最小,而β=12°时相比其他3个导叶安装角度下却有较明显的降低;整体看,在β=14°时,叶轮变形与应力在随流量变化时的变化率较为稳定,效果比其他导叶安装角度下的要好.

图6为0.8Qd和1.2Qd工况下的叶轮变形量ε分布,可以看出:最大变形量出现在前后盖板与叶轮流道出口中部相连接的部位,这是由于一方面在叶片出口处的水压力载荷最大,同时加上叶轮高速旋转产生的离心力共同作用导致,另一方面在外缘中部位置自身相比于其他位置缺少有效的加固结构;在0.8Qd工况下,叶轮进口边中部也出现相对较大变形量,而在1.2Qd工况下则未出现,这是由在0.8Qd工况下叶轮流道进口区域所产生的旋涡等不稳定流动造成的;整体看,随着导叶安装角度的增大,叶轮变形分布变得更加均匀,如在不同流道中前后盖板变形量最大部位的差值在β=16°时相比其角度下要更小,同时,虽然叶轮最大变形量随着导叶安装角度的增大而减小,但叶轮变形量较大的区域却是增加的.

图6 叶轮变形分布

图7为0.8Qd和1.2Qd工况下的叶轮等效应力δ分布,可以看出:最大等效应力出现在叶轮前盖板出口与叶片背面的交界处,这是由于此处结构特征较为尖锐,同时该区域相交关系所产生的约束较大,无法通过弹性变形释放应力,从而产生应力集中;0.8Qd工况下应力较大区域分布范围明显较1.2Qd工况下的大;在0.8Qd工况下,β=16°时叶片压力面出口中部有较明显的应力集中,随着导叶安装角度的减小,应力集中现象逐渐减小直至消失,这是由于随着导叶安装角度减小,叶片出口部位和导叶间的动静干涉逐渐减弱.

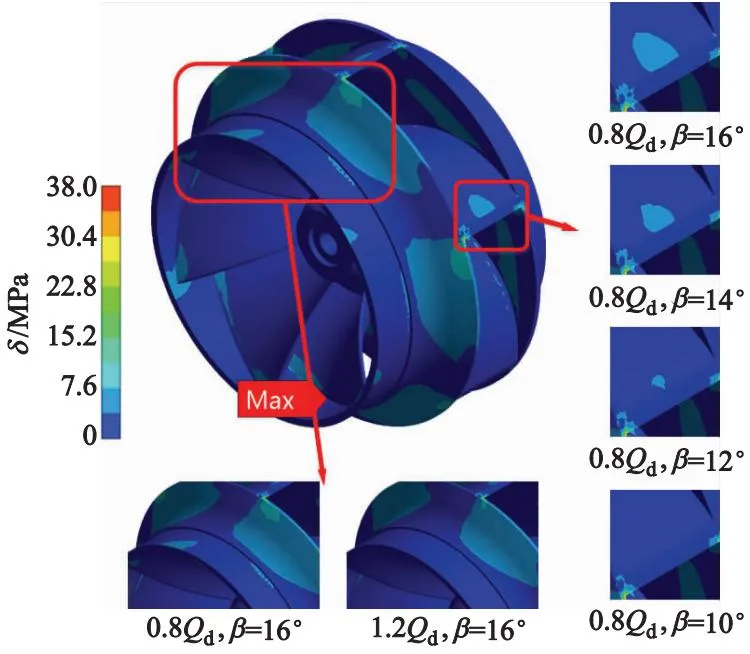
图7 叶轮等效应力分布

图8为在设计流量工况下,导叶安装角β=16°, 10°时在最后一圈叶轮的全局最大变形量和最大等效应力值变化曲线.

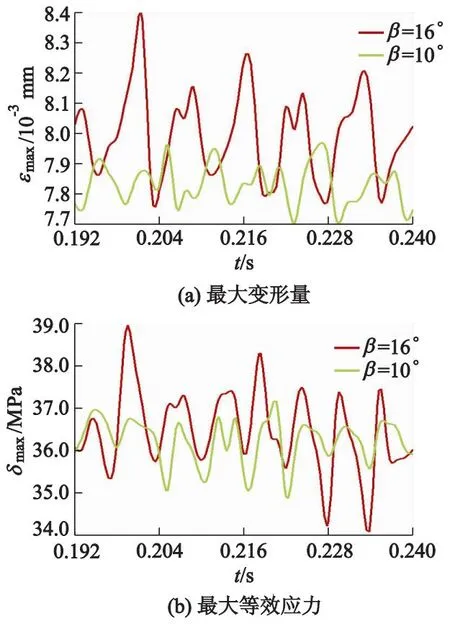
图8 瞬态变形与应力变化曲线

由图8可以看出,β=16°时的最大变形量和最大等效应力变化幅度要明显大于β=10°的,说明在非定常流动时泵内部水压力随时间变化较大,瞬态结构分析的峰值虽然比静力学分析的要大些,但其均值相差很小.

利用瞬态结构分析模块将非定常计算得到的水压力加载到叶轮结构上,发现叶轮的变形与等效应力分布以及变化规律与静力学分析下的结果基本一致,说明单向稳态流固耦合结果具有一定的参考价值.

3 叶轮模态分析

在Static Structural模块后添加Modal模块,得到叶轮结构在不同导叶安装角度时所产生的预应力下的模态.表1为β=16°时模型泵在设计工况下叶轮的固有频率和振幅对比,表中f1,f2分别为无预应力频率、有预应力频率,A1,A2分别为无预应力振幅、有预应力振幅.可以看出,与只添加固定约束的干模态进行对比,添加预应力的模态频率与振幅均无明显变化,因此是否添加预应力对叶轮模态的影响不大.

表1 有无预应力情况下的固有频率和振幅对比

添加Modal Acoustics模块,通过声固耦合法对叶轮结构进行湿模态分析,在叶轮内部与周围充满水,设置周围流体域厚度为40 mm,除添加固定约束外,将流体域外表面压力设置为0,并创建自动流固耦合交接面,如图9所示.

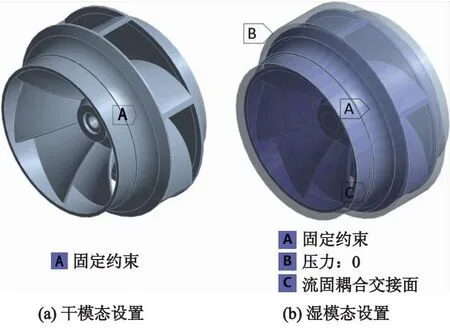
图9 干湿模态设置对比

表2为叶轮干湿模态对比,表中f3,f4分别为干模态频率、湿模态频率,A3,A4分别为干模态振幅、湿模态振幅.可以看出,由于水的附着力作用,湿模态固有频率与振幅均有下降,且随着阶数的增加下降更为明显.

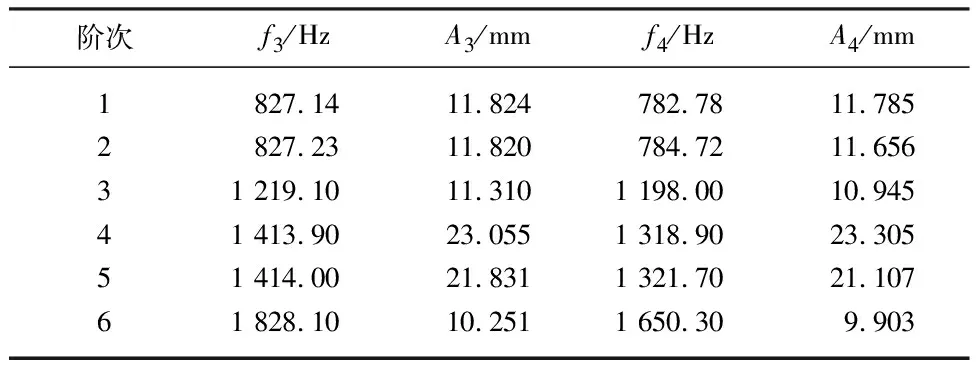
表2 干湿模态下的固有频率和振幅对比

4 结 论

对4种不同导叶安装角度的蜗壳泵进行数值计算和结构特性分析,得到结论如下:

1) 在小流量工况下,效率和扬程都随着导叶安装角度的增大而减小,而在大流量工况时相反,在设计流量工况附近时其差距最小.整体看,随着导叶安装角度减小,泵的高效区向小流量工况发生偏移,并且最高效率逐渐增大,最大提高达2.1%.

2) 通过单向流固耦合,得到稳态与瞬态的结果规律一致,叶轮最大变形量和最大应力值都随流量的增大而减小,在设计流量工况附近,都随导叶安装角度的减小而减小,最大差值达3.3%,且最大等效应力值变化较小,最大变形量出现在前后盖板与叶轮流道出口中部相连接的部位,最大应力出现在叶轮前盖板出口与叶片背面的交界处.

3) 不同导叶安装角度所产生的预应力对叶轮模态固有频率影响可忽略不计,湿模态下固有频率有较显著下降.