山丘区自压输水管道水锤计算与模拟方法

石晓悟,何武全,2*,李渤,段晓宁,田雨丰

(1. 西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100; 2. 旱区农业水土工程教育部重点实验室,陕西 杨凌 712100; 3. 中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065)

输水管道在中国被广泛应用于灌溉输水和城镇供水工程中以解决水资源配置和供水需求.然而在其运行期间,管道系统很容易出现突发状况,例如阀门突然关闭、水泵事故停机等,这些问题会引水锤现象,从而危害整个输水系统[1-2].山丘区自压输水管道因受到地形地势的限制,如何模拟、预测和控制输水水锤,防止其因水锤造成严重破坏是其备受关注的问题之一[3].

随着水锤理论体系的建立,不少学者对水锤的模拟计算方法不断改进[4-5].BEHROOZI等[6]基于局部多重二次微分求积法建立水锤数值计算模型,使水锤的计算不受空间网格的限制,降低了计算成本并提高了计算精度.练继建等[7]提出了不等空间步长的水锤分析方法,使得计算过程中对空间网格的划分更灵活,有不受管道系统中最短管道限制的优势.还有学者通过分析输水系统中的阀门特性,提出有效的防护措施[8].沈金娟[9]通过改进优化进排气阀的数学模型,提出了长距离输水管道进排气阀选型的方法.YAZDI等[10]提出了如何确定输水系统中防护设备的最优尺寸和布置等.但凡涉及管道输水工程,对水锤的模拟和防护是必不可少的环节.山丘区自压输水管道系统多由弯曲管道组成,对于弯曲管道的水锤分析,通常是将其直接近似为具有相同过流断面的直管来代替[11-13],然而水锤压力波在弯管内的传播和直管内的传播是不同的,直接近似为直管的计算方式会影响到整个计算的精度和可靠性.

文中以陕西省千阳县一实际自压管道输水工程为例,将弯管采用极限的思想进行拟合从而建立水锤计算数值模型,模拟计算该输水管道系统末端关阀时产生的水锤,并通过模拟不同的关阀方案实现管道系统的安全运行、提出相应的防护措施,在满足关阀时间要求的同时,将水锤危害降到最低.

1 数学模型及算法

1.1 倾斜直管的水锤计算

管道系统中的倾斜直管采用特征线法进行计算,有压管道的水锤基本计算控制方程包括连续性方程和运动方程[14],即

连续性方程

(1)

运动方程

(2)

上述式中:H为测压管水头,m;v为管道流速,m/s;t为时间,s;s为节点位置;θ为相对于水平线的管道角度,(°);a为水锤波速,m/s;g为重力加速度,m2/s;λ为摩阻系数;D为管道直径,mm.

1.2 弯曲管道的水锤计算

管道系统在山丘区的布置因受到地形地势的限制,通常会设有弯曲驼峰状的管道.对该部分采取极限的思想基于切线的曲线拟合矢量化方法[15],将弯曲管道拟合为沿管道中心线具有相同过流断面的多段等效直管来代替,各段等效直管采用特征线法进行水锤计算.

该方法的主要思想是通过提取弯曲管道中局部曲率极大值的节点,以这些节点作为端点将弯曲管道分为拟合管段,拟合管段中的局部切线作为拟合弯曲管道的依据,利用曲线可以由多段短直线拟合的极限思想,弯曲管道可以被沿管道不同节点即各切点之间的短直管道拟合进行水锤计算.

1.2.1 划分拟合管段

管道上每个节点,分别取其前后第b个节点,作为计算节点曲率的曲率近似范围点,如图1所示.

图1 节点的局部曲率计算

根据两点直线方程可以得出,弯曲管道中节点Pi-b和节点Pi+b的直线方程为

Ax+By+C=0,

(3)

其中

(4)

管道上节点Pi-b和节点Pi+b的弦长Lib为

(5)

点Pi到该弦的距离dib为

(6)

那么,点Pi的曲率为

(7)

利用式(7)可求得管道所有节点的曲率.求得节点的曲率越大,表明该点越可能是弯曲管道中弧度不连贯的转折点,通过寻找转折点将弯曲管道划分为更细致的连贯弧管段作为拟合管段.

1.2.2 管段拟合

以一段管道的拟合管段为例,如图2所示,以端点P0为起点作管道沿线的切线,弯曲管道上点到切线的距离为d的点P1作为下一条切线的起点.点P1是第1个拟合节点,以此类推,取完拟合管段上最后一个点到切线距离为d的点Pn.点Pn是最后一个拟合节点,连接管道上端点、各个切点以及终点Pz,即点P0,P1,…,Pn,Pz两两之间的短直管线用于拟合弯曲管段.

图2 管道片段的拟合

2 边界条件

2.1 上游水池边界条件

管道上游与已知水位的调节水池相连接,两者之间的连接处在很短的瞬变条件下,假设水池的水位恒定为常数值,同时利用有限差分法可得到关于连接处的进口节点计算流速的表达式,边界条件为

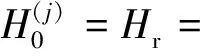
(8)

(9)

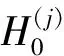
2.2 下游阀门边界条件

输水管道系统下游连接控制阀门时,边界条件根据孔口出流方程确定,阀门的相对开度τt随时间t的变化规律影响此时液体的流速和水头变化.

(10)

(11)

(12)

(13)

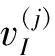
2.3 拟合管道内部连接条件

把弯曲管段的拟合短管道之间看作简单的管道串联,如图2所示,考虑水流在管道之间的正向流动,以一段弯曲管道拟合管段的连接情况,选取其中2段管道为例,流出段管道①末端节点的水头与流入段连接管道②初始节点的水头在瞬变的条件下可认为不变,连接条件当两者相等可表示为

(14)

此时关于2段连接管道流速的计算表达式为

(15)

(16)

其中

(17)

(18)

3 工程实例应用

3.1 工程概况

陕西省千阳县某管道输水工程,地处渭北旱塬西部丘陵沟壑区,管线沿途地形起伏较大.水源位于千阳县岭北坡的帽儿山,通过上游调节水池自压输水至下游蓄水池,输水管线全长1 984.10 m,上游调节水池设计水位高程为887.35 m,管道首端、末端高程分别为886.00和835.44 m,首末端地形高程差为50.56 m,管线末端设置有控制阀门.

该工程管道采用DN250-UPVC塑料管,壁厚7 mm,内径为236 mm.输送流体为水,体积弹性系数K为2.06×109N/m2,管壁材料的弹性系数E为3 300 MPa,泊松比为0.45.管线纵断面及稳态运行水头Hsr如图3所示,L为水平距离.经计算分析,稳态运行时,水流在管道内的流速为1.03 m/s,通过管道的流量为44.9 L/s,管线沿程的运行水头平稳逐渐递减,管线末端是管线高程的最低点,此处管道内水头最大达到44.280 m,水头损失为6.250 m.正常运行管线全程无负压,满足安全运行条件.

图3 管线纵断面及稳态运行水头

3.2 水锤模拟

为了验证文中所提出的弯管拟合等效短管与倾斜直管相结合的水锤计算模型,分别采用传统特征线法和文中提出方法对输水管道系统的水锤现象进行模拟.采用传统特征线法时,弯曲管道部分直接近似看作倾斜直管进行计算,取时间步长为0.015 8 s,空间步长为4.7 m.

文中提出方法则是通过提取整个管道中曲率极大值的节点,将整个管道系统划分为倾斜直管道和弯曲管道两部分,整个管道可分为28段倾斜直管道和21段弯曲管道,弯曲管道拟合为具有相同管径的多段等效直管,取时间步长为0.008 7 s,空间步长为最短的等效直管管长.在不采取防护措施的情况下,阀门经历10 s完全关闭发生水锤,图4为分别采用传统方法和文中提出方法的模拟计算结果对比,h为水头.

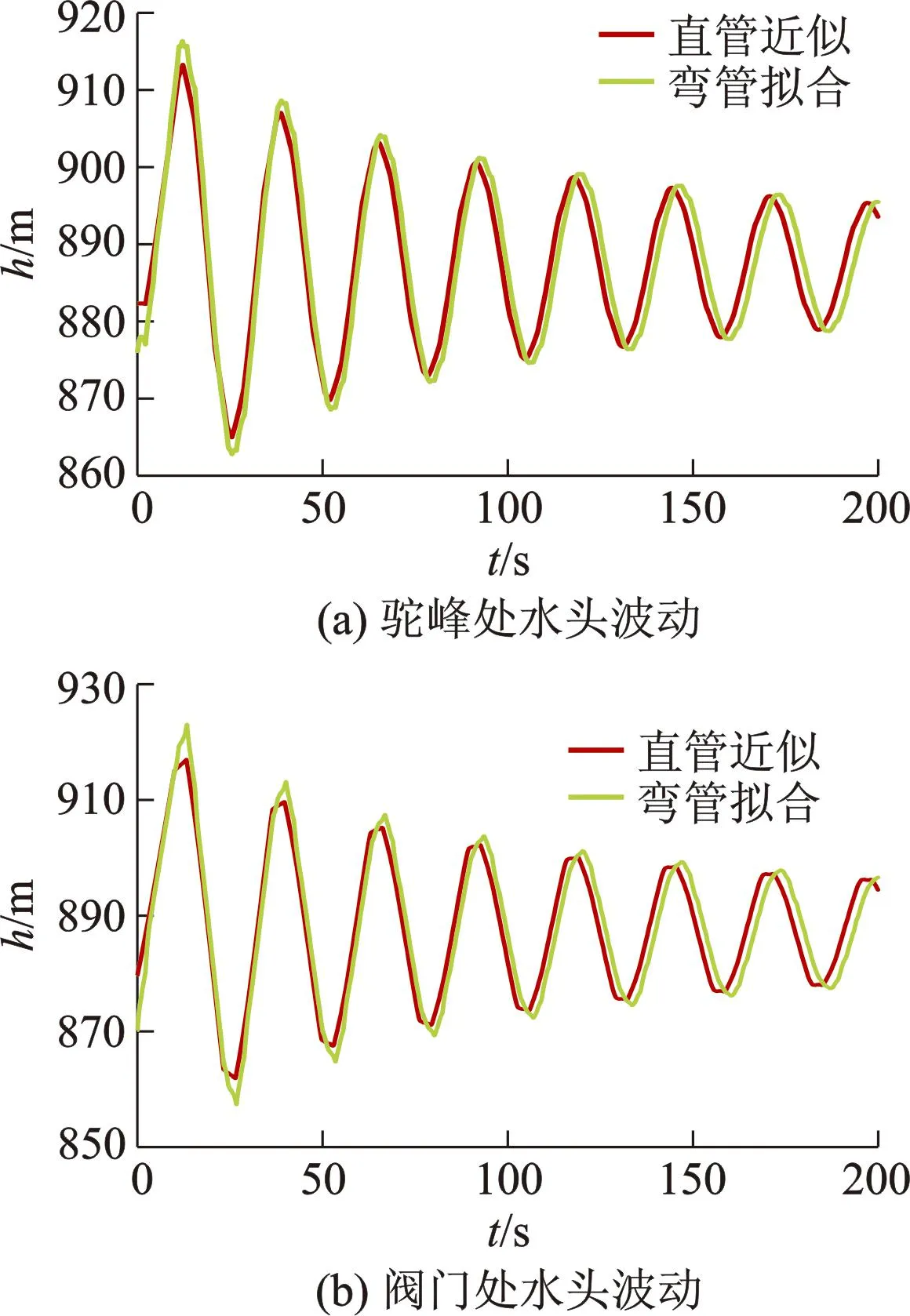
图4 2种方法的水头波动模拟结果对比

图4a显示的水头波动属于负压最大处的驼峰段(桩号K1+300),此处为弯管.从图中可以看出,采用2种方法模拟的结果趋势大致相同.但是,采用弯管拟合方法模拟所得的正负水头峰值明显高于传统方法,其计算结果与文献[16-17]中弯管的水头大于直管产生的水头的结论相符.由此可以看出,文中所提出的方法提高了水锤在弯管处的模拟精度,可以为预防驼峰处的负压提供参考.

图4b为管道末端阀门处的水头波动,从图中可以看出,采用弯管拟合方法模拟得到的阀门水头大于传统方法得到的水头值,也即相较于直接近似为倾斜直管道,采用弯管拟合的方法对弯管处水头的模拟结果亦会对管道末端阀门处的水头产生影响,其最大值由原来的916.978 m增大为923.021 m,增大了6.043 m,该增大值对实际工程产生的影响需引起重视.

3.3 最优关阀控制时间及水锤防护措施

水锤的压力波由阀门到水池传播一个来回所需要的时间段Ts称为一个相长.

(19)

对于该管道系统,如果阀门关闭时间T

选取该管道输水工程中桩号K0+497(驼峰1)、桩号K1+300(驼峰2)和桩号K1+710(驼峰3)3处可能产生较大负压的大起伏驼峰断面,以及产生水锤最大的阀门断面进行计算,分为10,15,20,30,40,50,60,80,120 s等9种不同的关阀时间工况,即管道系统末端阀门分别用以上9种关阀时间线性关闭,每次模拟运行时间持续200 s,采用文中提出的弯管拟合方法对工程中管道系统的水锤进行模拟分析.

为了便于分析计算结果,确定阀门关闭的最优时间,并提出相应的水锤防护方案,分别将9种关阀工况下,管道系统末端阀门处和3处驼峰位置产生的最大水头、最小水头进行比较,模拟计算结果见表1.

表1 不同关阀工况下水锤模拟计算结果

如果遇到突发情况管道末端阀门突然关闭时,从表1中可以看出,在没有采取防护措施的工况下,4处特征断面处正水头最大达到87.58 m,发生在管道末端的阀门处;3处驼峰位置均发生负水头,最小-3.09 m,最大达到-20.06 m,此时压力水头降至汽化压力水头(-10.00 m)以下,管道内可能出现汽化,对管道的危害极大.为了消减突发状况下的正、负水头给管道带来的破坏,应采用进排气阀和超压泄压阀联合防护的水锤防护措施.在3个大起伏驼峰最高点,也就是负压相对极大点设置进排气阀,当管道内出现负压时及时吸入空气从而达到消减负压的目的,在运行时进排气阀还可以排除管道内存在的气体;在末端控制阀门前设置超压泄压阀,当输水管道系统突然出现过高正压时及时打开超压泄压阀释放部分高压水,从而起到保护管道的作用.布置防护阀的具体位置和选型还需根据计算和规范进一步确定,从而更有效地满足该工程中水锤防护的要求.

输水管道系统运行中,如遇特殊情况需要关闭管道末端阀门时,可以寻求最优关阀时间来避免水锤对输水管道系统造成的破坏.图5为最大水头和最小水头随关阀时间变化情况.如图所示,当阀门关闭时间T>50 s以后,关闭阀门产生的水锤对管道系统的压力影响逐渐减小并趋于稳定,压力影响发生变化的转折点作为关阀最优控制时间的上临界点.此外,考虑到工程运行中关阀时间不宜过长,从图5中可以看出,当阀门关闭时间T>120 s后,压力变化与之前的工况比较变化很小,因而将120 s关阀时间作为最优控制时间的下临界点.

图5 最大水头和最小水头随关阀时间变化图

因此,该工程实例中最优的关阀时间确定为50 s≤T≤120 s.

4 结 论

1) 针对山丘区长距离输水管道系统的特点,提出了将输水管道系统分为弯曲管道和倾斜直管相结合的水锤计算方法,弯曲管道采用极限的思想拟合为多段等效直管,建立了自压输水管道的数值计算模型,提高了水锤的计算精度.

2) 以陕西省千阳县一山丘区长距离自压输水管道工程为例,采用特征线法与文中所提方法分别进行水锤计算分析,并通过比较模拟计算结果验证了该方法的合理性.

3) 通过模拟该工程9种不同关阀时间工况下产生的水锤情况,分析对比并提出了相应的水锤防护措施,得到了工程运行中关阀的最优时间.所提出的方法可为山丘区长距离自压管道输水工程建设与管理提供参考.但所提方法未进行水锤试验与实测值验证,今后仍需进一步研究.