B-Spline曲线聚风装置直线翼垂直轴风力机启动性能数值模拟

李岩,马云飞,佟国强,杨胜兵,肖振军

(1. 东北农业大学工程学院,黑龙江 哈尔滨 150030; 2. 寒地农业可再生资源利用技术与装备黑龙江省重点实验室,黑龙江 哈尔滨 150030)

中国长期坚持大力发展绿色能源,随着“3060”碳达峰碳中和目标的实施,分布式发电和离网发电因其具有节省投资、降低能耗以及提高电力分配灵活性的特点,成为研究与发展节能减排的重要举措之一[1-4].其中小型风力机的研究和应用一直是研究的热点[5-7];垂直轴风力机(vertical axis wind turbine, VAWT)尤其是直线翼垂直轴风力机(straight-bladed vertical axis wind turbine, SB-VAWT)在近年来得到了长足的发展[8-10].

然而,垂直轴风力机由于下游叶片来流能量损失较大,且叶片在某些角度会产生阻力,影响启动,所以启动性能相对较差是限制其应用的最重要原因之一[11].研究人员已从不同角度对直线翼垂直轴风力机的启动性能进行优化[6],例如KATO等[12]开发了TWT系列的特殊翼型.此外,一些研究人员改变了叶片形状,使叶片具有一定的阻力剖面,在低风速下的起动性能得到改善[13].ABDALRAHMAN等[14]研究了不同叶尖转速比下叶片节角的变化.莫岳平等[15]设计了一种基于最佳叶尖速比的模型自校正复合自抗扰控制器.WANG等[16]对螺旋叶片进行了一系列三维数值模拟,并将其与传统的直线翼垂直轴风力机进行了比较.姬俊峰等[17]提出了一种沿来流方向在直线翼垂直轴风力机周围安装防风罩的方法,可以引导来流并提高风轮附近来流风速.CHONG等[18]提出了带全方位导叶的直线翼垂直轴风力机,提高了风轮的风能利用率.黄娟等[19]还提出了一种带导叶的直线翼垂直轴风力机,导叶沿来流方向安装在转子周围,研究结果表明导叶改善了风轮的启动性能.以上设计的聚风装置都是利用XOY平面的气流,但Z坐标轴方向的来流聚风效果欠佳.文献[20-21]创新地提出了一系列棱台、圆外形型的聚风罩(wind gathering device, WGD),该系列装置可以安装在距风轮的上、下端面一定距离处,以聚集包括Z轴方向在内的风轮迎风面的来流,并提高风轮附近来流风速.

文中利用B-Spline曲线生成方法,对聚风装置的主要外形结构参数进行进一步研究和优化,以设计出具有凸流线型的聚风装置.

1 聚风装置B-Spline曲线生成原理

在风轮上下加装聚风装置可显著提升直线翼垂直轴风力机的启动性能;聚风装置的空气动力学外形结构直接影响其捕风及加速来流的能力.

SCHOENBERG于20世纪40年代提出了B-Spline曲线.如今由DE BOOR和COX分别提出的递推定义[22],可表示为

(1)

式中:k为B样条的幂次;t为节点;下标i为B样条的序号.

从式(1)可以得出,欲确定第i个k次B样条Ni,k(x),需要ti,ti+1,…,ti+k+1共k+2个节点,方程中n+1个控制顶点di(i=0,1,…,n)要用到n+1个k次B样条基函数Ni,k(x) (i=0,1,…,n).

由式(1)得出,k次B-Spline曲线的参数为x∈[ti,ti+1]的一点P(x)至多与k+1个顶点dj(j=i-k,i-k+1,…,i)有关,与其他顶点无关[22].

图1为B-Spline曲线示意图.研究中的聚风装置曲线轮廓由类似于图中所示的红色曲线由三次四阶B-Spline曲线构成,具体的设计方法与参数将在下文第2.2条介绍.

图1 B-Spline曲线示意图

2 模型设计与研究方法

主要通过使用ANSYS-Fluent软件进行数值模拟,将不同设计参数的各组聚风装置分别与3叶片风轮组合,进行二次旋转正交组合,并筛选最优模型.

2.1 直线翼垂直轴风力机

在数值模拟中建立的风轮模型所采用叶片为3枚对称翼型NACA0018,弦长100 mm,叶片高度为500 mm,旋转半径为300 mm.图2为风轮平面工作示意图.定义三叶片风轮如图2a位置时,上段叶片弦长与来流方向平行,方位角记为0°;旋转一定角度后,此时方位角如图2b记为φ.

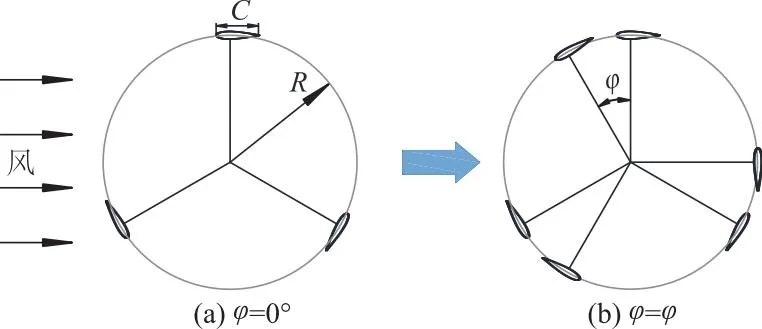
图2 风轮方位角示意图

2.2 聚风装置设计

图3为聚风装置设计图,聚风装置设计共选取5个结构设计参数,分别为聚风装置与风轮间隙距离ΔL、聚风装置底圆半径R1、聚风装置顶圆半径R2、入口角α1和出口角α2.图3a中以红色标出的聚风装置曲线轮廓为设计部分,具体设计方法如图3b所示.聚风装置的厚度h设为150 mm.当聚风装置有确定的R1和R2时,设R1端点为P1,R2端点为P4.点M和点N均为线段P1P4上的三等分点,分别过点M和点N作线段P1P4的垂线;再过点P4作一条射线,射线与线段P1P4的夹角为α1.显然,来流进入聚风装置后,气流的偏转角为α1与β1的角度之和.因为当h,R1和R2确定时,角度β1固定不变,α1是影响气流偏转角的唯一因素,故设α1为入口角.同理,过点P1作一条射线与线段P1P4的夹角为α2,称为出口角.所作的两条射线分别与过点M和点N的两条垂线相交,交点分别为P2和P3.将点P1,P2,P3和P4作为生成三次四阶B样条曲线的4个控制点,得到了图3b中聚风装置的凸流线型轮廓.

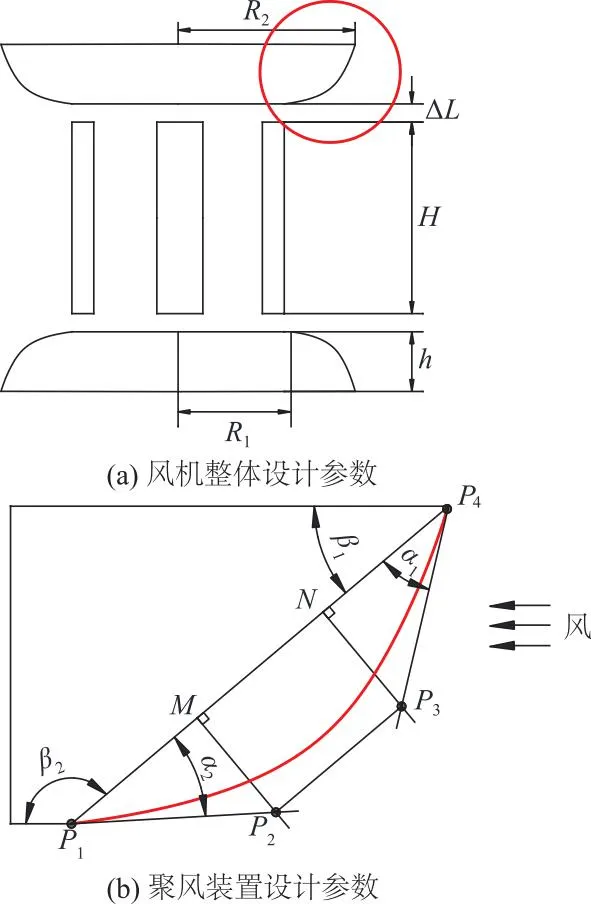
图3 聚风装置设计图

2.3 数值模拟研究方法

2.3.1 计算域与边界条件设置

研究采用SSTk-ω湍流模型[23].风速U设为4 m/s.k和ω的值由风速、空气的流体密度和动力黏度以及风轮的旋转直径确定.压力-速度耦合采用SIMPLE算法.设置压力、动量、湍流动能和比耗散率的二阶迎风模式,残差设为欠松弛因子0.7,收敛误差设定为1.0×10-6,其他操作选择默认值.计算域如图4所示,D为风轮旋转直径.为方便动态流场计算,将计算区域划分为静态区域和旋转区域.

图4 计算域示意图

2.3.2 网格无关性验证

对上节所述模型采用非结构四面体网格,采用相同的网格生长方式,调节全局网格参数生成10种数量递增的网格进行计算,结果如图5所示,图中Cmas为平均启动力矩系数,Ng为网格数.

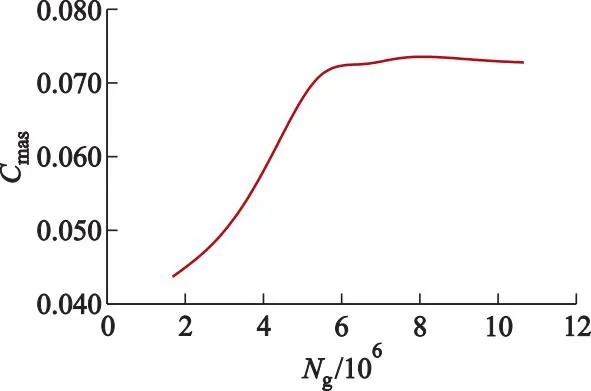
图5 各网格数对应的平均启动力矩系数(φ=100°)

根据计算结果,在网格数达到750万后,网格数继续增长但数值模拟结果变化微弱.所以选择750万作为网格数,并根据聚风装置的形状变化进行微小调整.

3 聚风装置对风力机性能影响

3.1 聚风装置参数优化

3.1.1 二次旋转正交组合设计

以团队以往研究[24]做参考,聚风装置5个设计参数均取整.具体五因素五水平编码见表1;式(2)为优化所得回归方程.

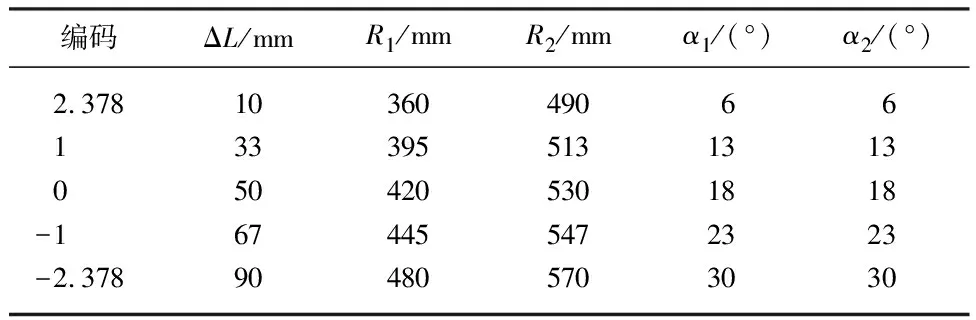
表1 因素水平编码表

(2)

式中:x1,x2,x3,x4,x5分别表示聚风装置与风轮间隙距离ΔL、聚风装置底圆半径R1、聚风装置顶圆半径R2、入口角α1、出口角α2;Y表示风力机平均启动力矩.

3.1.2 响应面分析

根据式(2)中显著的交互项x1x3,x2x4,x2x5分别绘制以风力机平均启动力矩Mas(average starting moment)为指标对应的ΔL和R2,R1和α1,R1和α2的三维响应曲面图,结果如图6所示.分析时其余因素均取0水平,得出聚风装置的最佳设计参数:ΔL为60 mm,R1为412 mm,R2为542 mm,α1为19°,α2为23°.模型如图7所示.采用此最佳参数组合进行数值模拟并对结果进行分析.

图6 交互项响应面分析

图7 优化后聚风装置示意图

3.2 聚风型风力机平均启动力矩系数及静态流场

3.2.1 平均启动力矩系数分析

图8对比了不同风速下风轮处在各方位角φ时,有无加装聚风装置的平均启动力矩系数Cmas特性.由图可知,各风速下有无聚风装置的风力机的Cmas随φ变化波动趋势基本一致.除去方位角10°的情况,装有聚风装置的风力机的启动性能在其余角度均优于无聚风装置的风力机.而在方位角为10°时,4个风速下的偏差仅为4.6%～5.5%.说明聚风装置能够整体提升风轮的启动特性.2种风力机在方位角0°～120°内Cmas曲线趋势均为波峰-波谷-波峰.曲线在方位角20°和100°时Cmas达到极大值,100°时为最大值(风速10 m/s的情况下,在30°和100°时达到极大值,100°时为最大值).在方位角0°和50°下达到极小值.

图8 2种风力机的平均启动力矩系数

第1个波峰时,2种风力机最大的Cmas值均在U=10 m/s时取到,聚风型风力机为0.081 6、非聚风型风力机仅为0.066 0,提升了23.6%.而提升效果最佳的工况在U=5 m/s时取到,聚风型风力机为0.073 6、非聚风型风力机仅为0.058 4,提升26.0%.

第2个波峰时,2种风力机Cmas最大值均在U=10 m/s时取到,聚风型风力机为 0.091 4、非聚风型风力机仅为0.073 3,提升24.7%.而提升效果最佳的工况在U=5 m/s时取到,聚风型风力机为0.080 3、非聚风型风力机仅为0.061 2,提升了31.2%.

图9和图10分别表示不同方位角下各风速的Cmas增量变化ΔCmas和Cmas提升百分比P(Cmas);表2为单个周期内Cmas的平均提升量.由图9可知,聚风型风力机仅在10°方位角时Cmas有微量的下降;在其余方位角时,则均有不同程度的提升.Cmas在方位角为20°～30°和80°～110°内增长明显.聚风装置对风力机自启动性能提升的角度范围,高达全部方位角的91.7%.将单个周期内各角度Cmas提升百分比的平均值和Cmas提升百分比最高的角度个数作为筛选聚风装置最佳工作风速的判据.由表2可知,U=5和4 m/s时,Cmas提升效果较好,其中U=5 m/s的Cmas平均提升百分比为24.7%.

表2 单个周期内Cmas的平均提升量

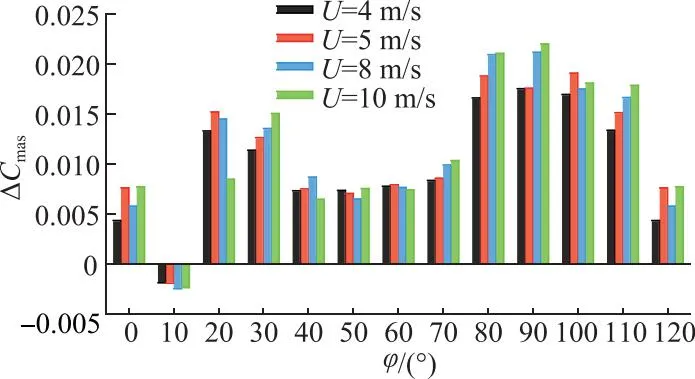
图9 聚风型风力机Cmas增量

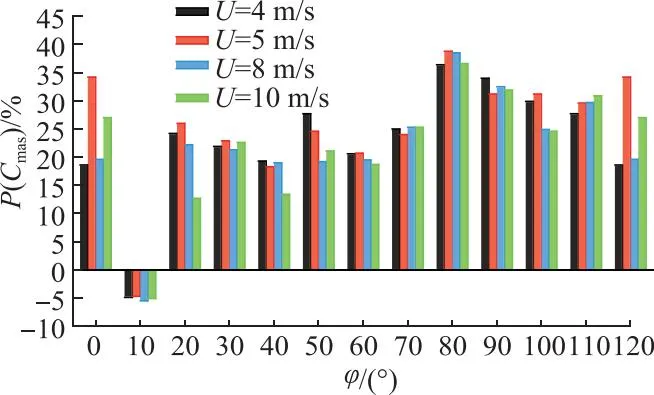
图10 聚风型风力机Cmas提升百分比

又由图10可知,当U=5 m/s,在方位角为0°,10°,20°,30°,60°,80°和100°时,Cmas提升百分比均为各风速下最高,并在80°达到最大,为38.8%.在一个周期内,提升效果为各风速条件下最高的角度个数,U=5 m/s时的占比达58.3%.由此可知,U=5 m/s为聚风装置的最佳工作风速.照此方法,U=4 m/s为第二适宜工作风速,提升效果为各风速条件下最高的角度占比达25%.

3.2.2 压力场分析

图11为选取叶片中心水平面z=0、叶片顶部端面z=0.25 m为研究对象,在工作风速U=5 m/s、风轮处在φ=100°(Cmas最大)时,叶片附近的压力p分布情况.叶片分别为blade1,blade2和blade3,记为b1,b2和b3.由图可知,风轮在φ=100°时,各截面的压力分布较为相似.在截面z=0处,b1的正负压区规则地分布在叶片两侧,根据正负压各自的中心位置可以看出:b1产生正力矩,对风轮启动有积极影响;b2尾缘和腹面存在正压区,前缘和背面存在负压区,所以b2受气动合力推动,产生正向的启动力矩;b3则因为腹面正压和背面负压的共同影响下产生阻力,对风轮启动有负面影响.在截面z=0.25 m处,b1所受的气动合力几乎与b1所在的半径平行,对风轮启动影响微弱;b2与b3分别与其自身在截面z=0时的状况类似.

图11 2种风力机的叶片压力场分布

由加装聚风装置后的压力分布可知,聚风装置对各截面压力分布有极大改善.在截面z=0处,由于聚风装置的聚风效果,b1的正压区面积呈放射状大幅度增加;负压区面积同样获得了扩大,绝对值增加,且负压中心下移.b1在腹背面压力梯度增大的优势背景下,因负压中心向下偏移,使b1产生的转矩在启动方向的分量大幅提升.b2的负压区也产生了类似于b1的扩张与偏移,同样导致了b2产生的转矩在启动方向的分量大幅提升.不仅如此,b2的腹面靠近前缘处存在负压区,更进一步地增加b2产生的启动力矩.b3的正压区减小,腹背面压差降低,减少了阻力的产生.

在截面z=0.25 m处,b1的正压区与聚风装置产生的高压区相接,负压区扩大,中心下移,并蔓延过叶片前缘.由于b1所受气动合力向启动方向偏移,且前缘阻力降低,所以b1产生的启动力矩有所提升.b2与b3的负压区均扩大且向前缘方向移动,在提升自身输出力矩的同时,也减少了启动阻力.

3.2.3 速度场分析

为了直观探究聚风装置加速风轮附近的来流效果与叶片附近的流动规律,提取截面z=0和z=0.25 m,在U=5 m/s的情况下,研究风轮φ=100°时的速度云图,如图12所示.由图可知,在截面z=0处,无聚风装置的情况下,叶片附近由于存在压力梯度,导致叶片正负压区产生局部加速流动,出现较高的风速.叶片附近出现面积最大的涡旋,涡旋会消耗叶片的动能,造成更大的阻力,并且会减少叶片上、下表面的压力差,进而减少气动合力.在加装聚风装置后,风轮附近的流速明显整体上升.且叶片前后速度差增大,汲取更多风能,并且极大地减少了涡旋的产生,进而减少能量[22]损失,使叶片能量转换的效率得以提升.

图12 2种风力机的叶片速度场分布

在截面z=0.25 m处,无聚风装置的情况下,风轮旋转范围内的流速大部分集中在5 m/s左右,气体从端面流过并汇集在叶片背风面.各角度下叶片的尾流速度较高,能量利用率较低.在加装聚风装置后,在靠近聚风装置壁面,由于壁面与叶片端面距离较近,对局部气体产生了更强的加速作用,所以流速提高的区域呈圆形分布.各叶片迎风面与背风面之间的速度梯度存在不同程度增大,能量利用率提高,其中2个下游叶片的变化较为明显.但下游叶片的前缘产生了较小涡旋,耗散了部分能量.

综上所述,聚风装置可以显著提升自身内流道的气体流速,提供能量密度较高的来流.同时,对不同角度下叶片的尾流均有较大程度改善,体现为降低局部气流紊乱程度、减小涡旋带来的能量损失,最终提升风轮的启动能力.同时聚风型风力机在叶尖端面处对叶片能量利用率的提升有很大的促进作用,但下游叶片产生涡旋的问题值得今后再做进一步研究,以进一步提升启动性能.

4 结 论

为提升直线翼垂直轴风力机的启动特性,基于B-Spline曲线生成方法,利用二次旋转正交试验设计筛选性能最优的聚风罩装置,运用数值模拟计算获得优化后聚风型风力机的启动特性.通过分析其平均启动力矩系数Cmas特性和压力场、速度场分布规律,得出以下结论:

1) 通过B-Spline曲线生成方法设计、二次旋转正交数值模拟优化后的聚风装置,明显提升了直线翼垂直轴风力机的启动性能.

2) 聚风装置与风轮组合后的聚风型风力机最佳工作风速为5 m/s,此时的平均启动力矩系数平均提升百分比为24.7%.在φ=80°时,Cmas提升最大,最高可达38.8%;在φ=100°时,Cmas达到峰值,相比无聚风型风力机最大可提升31.2%.

3) 通过压力场分析,得到聚风装置优化风轮启动特性的机理:① 改善叶片压力分布,增大叶片腹背面压差提升压力梯度,使叶片受到更大的气动合力;② 优化压力分布位置,产生更多有效正力矩;③ 减少叶片前缘阻力促进风轮启动.这3种优化方式的共同作用,使直线翼垂直轴风力机的启动性能获得明显的改善.

4) 通过速度场分析,聚风装置可以显著提升自身内流道的气体流速.对叶片尾流均有较大程度的改善,可以减小叶片产生的涡旋带来的能量损失,促进风轮的启动能力.