CAP1400核主泵叶轮动应力计算及疲劳寿命预测

汪家琼,王瑞芝,付强,朱荣生,徐伟,王耽耽

(江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)

叶轮是核主泵的核心部件,其作用是驱动冷却剂在核主泵中顺利流动.在核主泵实际运行过程中,叶轮直接接触高温、高压、强辐射的冷却剂流体,在工况变化或事故情况下,流经叶轮的流体温度、压力、流量会发生较大变化,叶轮可能会产生较大的应力及变形,将造成叶轮结构损坏,进而影响核主泵的安全稳定运行.同时,冷却剂循环带来的流量波动,使得叶轮承受由转子-定子干涉引起的周期性压力脉动[1-2].在核主泵60 a的设计寿命周期内,叶轮将在高温高压环境中运行上万次循环,同时受到周期性压力载荷的不断作用,叶轮承受应力值虽低于材料屈服极限,但仍可能发生疲劳破坏[3-4].然而,这类问题无法通过静强度分析和预测.因此,对叶轮的动力学特性和疲劳寿命进行分析对提高核主泵运行稳定性具有重要意义.

目前,国内外学者在流体机械核心部件的内部流动和力学特性方面做了大量研究.ZHOU等[2]、ZHANG等[5]分别对核主泵中转子-定子干涉引起的压力脉动特性进行了数值研究.NI等[6]将压力脉动测量方法和激光多普勒测速仪(LDV)相结合阐述了核主泵内部流动特性.钟伟源等[7]采用双向流-固耦合方法研究了核主泵叶轮应力和变形分布规律.朱荣生等[8]采用流-热-固耦合方法研究得到不同温度下不同材料的高温泵结构应力及变形规律.李颖[9]采用ANSYS/Fe-safe分析得到核主泵叶轮疲劳寿命分布云图.李璞[10]、吴广宽等[11]对水轮机转轮叶片出现裂纹原因进行分析,认为裂纹是由于叶轮承受交变动应力造成的.上述研究主要集中在旋转部件的内部流动特性以及流-固耦合作用下结构的应力变形分布情况,而对高温下核主泵叶轮结构的动应力分析和疲劳寿命预测较少.

流-热-固耦合[12]计算包括单向耦合和双向耦合.如果结构变形较大,则会导致流道区域变形,需选择双向耦合.如果结构的变形非常小,则单向耦合计算是可行的.文中数值计算采用CAP1400核主泵原型泵,与叶轮直径相比,叶片变形可以忽略不计,因此采用单向流-热-固耦合对叶轮承受的结构应力进行计算.将CFD计算得到的流体压力载荷和温度载荷传递给结构并施加离心力、重力等惯性力载荷进行应力分析,并基于MATLAB实现雨流计数法对应力-时间历程数据的统计分析,采用线性疲劳损伤累积理论对叶轮的疲劳寿命进行预测.

1 计算模型及设置

1.1 计算模型及网格划分

以CAP1400核主泵原型泵[4,13-14]为研究对象,其基本参数分别为设计流量Q=21 642 m3/h,设计扬程H=111 m,额定转速n=1 480 r/min,叶轮进口压力p=15.5 MPa,叶轮进口温度T=280.6 ℃.

流体域模型主要包括进口段、叶轮、导叶、蜗壳等.采用ICEM CFD对流体域划分5套不同网格方案,并进行网格无关性检验.当模型网格数大于360万时,扬程预测偏差小于1%.因此,考虑计算资源与计算精度,最终确定后续计算总网格数约为360万,总体网格质量在0.44以上.网格划分如图1所示,其中叶轮、进口段、导叶、蜗壳水体网格单元数分别为46.9万、143.5万、110.0万、59.7万.

图1 网格划分

固体域模型采用NX进行建模,主要包括核主泵叶轮和主轴.在ANSYS Workbench中采用自适应网格划分,综合考虑耦合计算资源和计算精度,由稳态流-热-固耦合计算的网格划分结果确定为瞬态流-热-固耦合计算的网格方案.考虑网格数会对应力计算结果产生影响,在Workbench结构模块中设置网格最大加密循环为5,加密深度为2,随着网格密度的减小,自适应网格在最大应力处进行自动加密.同时,对等效应力(equivalent stress)计算设置收敛条件,即允许应力波动2%时停止网格自动迭代,最终确定总网格节点数为1 122 029.

1.2 边界条件设置

1.2.1 计算边界条件

由于核主泵处于高温高压的工作环境,难以搭建试验台进行试验,故流-热-固耦合计算采用数值模拟方法.根据核主泵基本参数,应用ANSYS CFX进行非定常流热场计算,非定常计算以定常计算结果为初始条件,并结合核主泵运行条件[2,13],在CFX-pre中设置边界条件总压和总温进口、质量流量出口.转子部件和定子部件的动静耦合作用通过“Interface”进行传递.定常和非定常计算的坐标系变换分别采用“frozen rotor”和“transient rotor stator”模式.以叶轮旋转2°为一个时间步长,即0.225 20 ms,一个周期为0.040 54 s.

CFX数值计算结果以插值映射法在ANSYS Workbench中实现流体压力载荷和温度载荷向Mechanial的传递.同时,设置2个圆柱约束分别在主轴上安装轴承的位置,施加离心力载荷在叶轮上,施加固定载荷在轴末端,整体施加重力载荷.约束布置如图2所示.

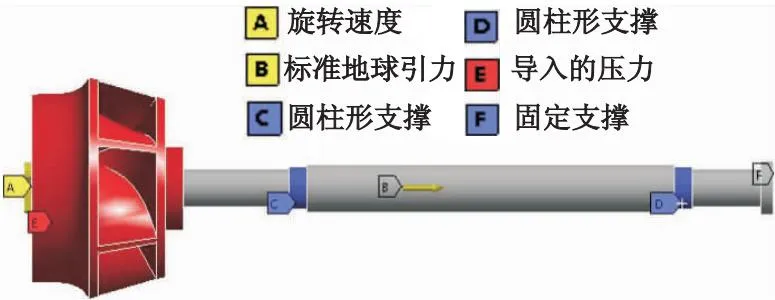
图2 固体域模型及约束布置

1.2.2 材料定义

流经叶轮的冷却剂为高温高压的硼酸溶液,其对叶轮的影响可以不计[15].因此,设定输送介质为清水.叶轮工作条件下,水的物性参数分别为摩尔质量M=18.02 g/mol,密度ρ=763.25 kg/m3,定压比热容cp=5.09 kJ/(kg·K),动力黏度μ=9.63×10-5Pa·s.叶轮材料[16]选用ASME 182 F6NM(13Cr4Ni),材料抗拉强度σb=620 MPa,屈服强度σs=525 MPa,在ANSYS Workbench中添加材料属性,并设置其随温度变化,其他相关参数由文献[17]获得.

2 数值计算结果及分析

2.1 流-热耦合下叶轮内部流动分析

2.1.1 温度场分析

图3为设计流量工况下叶轮和导叶在不同叶珊展向Span上的温度分布,各小图中左侧为叶轮,右侧为导叶.

图3 不同展向温度分布

由图3可以看出:在叶珊展向Span=0.1时,叶轮叶片进口边吸力面上均存在部分温度较高区域,但局部存在一些差异,这是由于一方面叶片附近流动受到导叶和蜗壳出口相对位置变化的影响,另一方面此处靠近叶轮轮毂,流体流入叶轮后,在重力作用下,流体对叶片进口边的冲击以及摩擦产生少量热量积累所致;在Span=0.5时,叶轮各流道内温度分布基本一致,但叶轮叶片吸力面上的温度有所降低(见图中虚线);在Span=0.9时,即靠近叶轮轮缘处,流道内温度分布比较均匀.

整体看,叶轮流道流体温度变化小于0.300 ℃,说明清水介质密度设置为定值是合理的.分析温度变化小的主要原因:一是核主泵的热源来自于进口处的热流,内部无其他发热源;二是流体在流道中停留时间短,叶轮做功产生热量与流体在流道中流动的热量损失基本相互抵消.

2.1.2 压力场分析

图4为设计流量工况下叶轮和导叶在不同叶珊展向上的压力分布,可以看出:叶轮叶片压力面的压力明显比吸力面的高,压力在不同流道分布相似,但在局部存在差异,这是由于导叶和蜗壳的存在,使得叶片附近流动随蜗壳出水口及导叶的相对位置变化而不同;在叶片进口边吸力面上出现部分低压区,这是由于流体进入叶片后冲击进口边,产生二次流,导致进口边出现部分低压区域,且压力梯度大,这也是易产生汽蚀的部位.

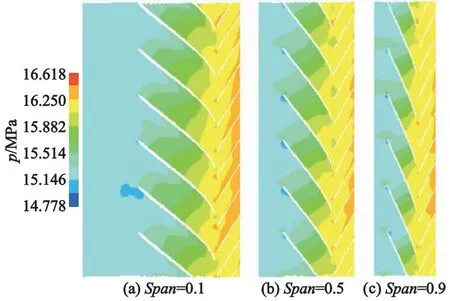
图4 不同展向压力载荷分布

整体看,在叶轮进口至叶片进口区域压力基本恒定,当流体流入叶片时,叶轮开始做功,压力逐渐上升,直至叶轮出口处达到最大值.

2.1.3 速度场分析

图5为设计流量工况下叶轮和导叶在不同叶珊展向上的流场速度分布,可以看出:在Span=0.1时,即靠近叶轮轮毂处,流体进入叶轮后连续绕流叶片,由于流体冲击叶片会产生部分水力损失,使得近轮毂处叶片附近流体速度较低;在Span=0.5时,即位于流道中间位置,叶轮叶片压力面的流速明显比吸力面的小,流体速度在各个流道分布较为均匀,这说明湍流得到了充分发展,此时能量损耗也相对较小;在Span=0.9时,即靠近轮缘处,由于叶轮旋转产生离心力的作用使得流速进一步提高.

图5 不同展向速度场分布

2.2 流-热-固耦合下叶轮应力分析

2.2.1 叶轮结构应力总体分布

图6为在设计流量工况下,t=0.405 40 s时,叶轮等效应力S分布及应力集中细节.

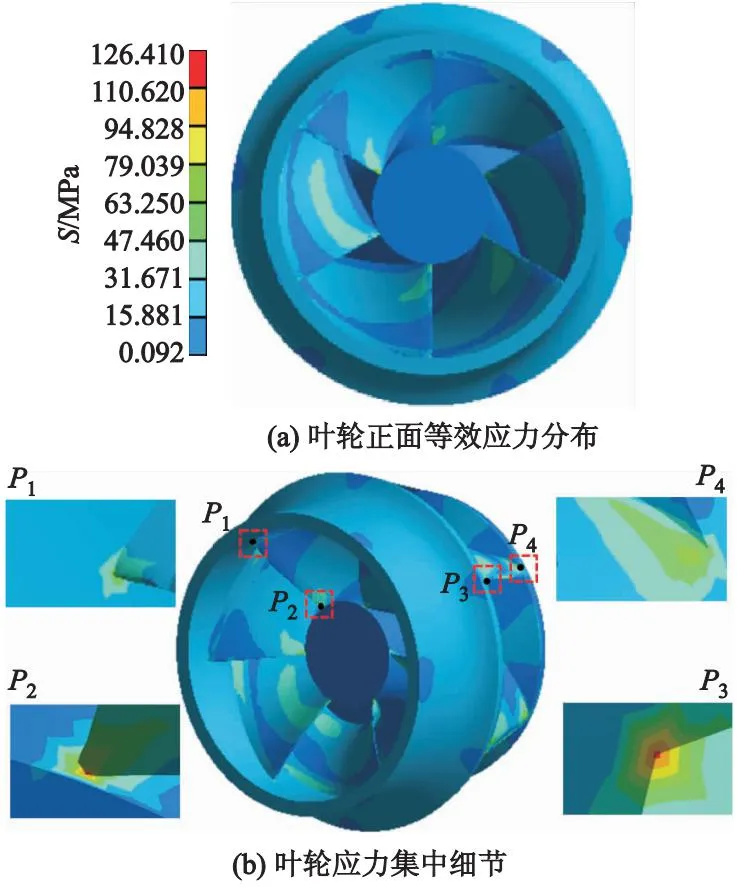
图6 叶轮等效应力分布

由图6a可以看出:叶轮应力在各个流道分布基本相似,但局部存在差异,这主要由于叶轮叶片受力随导叶和蜗壳出水口位置不同而发生变化;由于水流与叶片进口边相互作用较为强烈,使得叶片进口边出现部分较高应力区域.

由6b可以看出:叶片出口边的应力明显大于叶片进口边的应力,这是由于一方面叶片在出口边受到导叶对叶轮的动静干涉作用较为强烈,另一方面叶片旋转推动流体做功,出口边压力达到最大所致;叶轮叶片进、出口边与前、后盖板交接处4个区域容易产生应力集中(具体细节见各小图,其中监测点P1,P2分别位于叶片进口边与前、后盖板交接处,监测点P3,P4分别位于叶片出口边与前、后盖板交接处),这表明叶片进出口边对液流方向的改变比较敏感;同时,叶轮最大等效应力值出现在叶轮出口边与前盖板交接处.

2.2.2 叶轮进出口边动应力分析

叶轮应力最集中的部位主要在叶片进、出口边与前、后盖板交接处,即该4处为叶片的危险部位.为分析上述危险部位的动应力变化规律,在应力集中区域分别设置4个监测点,分别为P1,P2,P3,P4(见图6b).

图7为设计流量工况下4个监测点在10个叶轮周期的应力-时间历程,可以看出,各监测点动应力峰值和峰谷出现时间基本相同,而波动幅度不一致,且各点应力随时间变化均呈现出周期性.

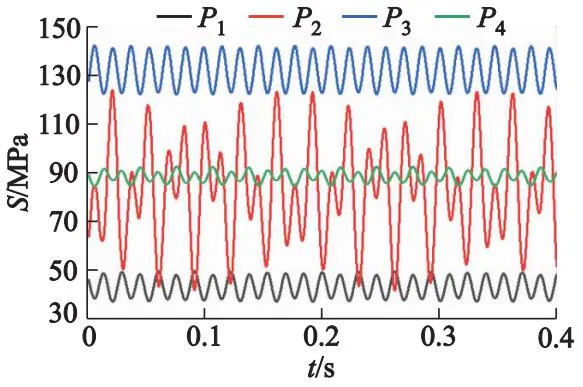
图7 各危险部位应力-时间历程

对各危险部位的应力-时间历程数据进行统计,如表1所示,表中Sm为应力均值;Sv为应力谷值;Sp为应力峰值;Sa为应力幅值.

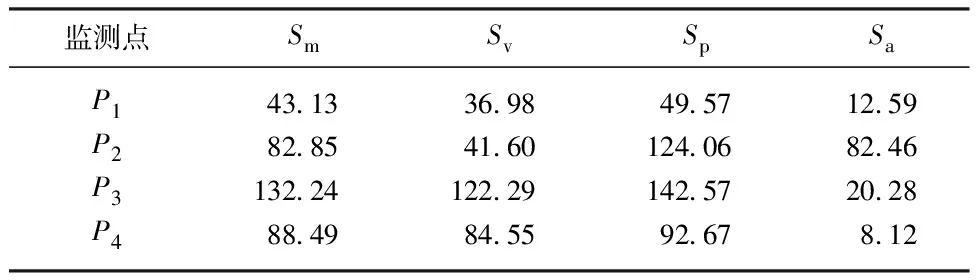
表1 应力数据统计

由表1可以看出,危险部位应力最大值均出现在叶片出口边与前盖板交接处,叶片进口边与后盖板交接处以及叶片出口边与后盖板交接处次之,叶片进口边与前盖板交接处动应力值最小.

叶片进口边与前盖板交接处动应力最大为142.57 MPa, 由第四强度理论可知,叶轮满足强度要求.计算应力均在材料的屈服极限内,这说明在此应力下发生的疲劳为应力疲劳.叶轮叶片进口边与后盖板交接处应力幅值最大,为82.46 MPa.因此,初步确定易产生疲劳破坏位置为叶片出口边与前盖板交接处和叶片进口边与后盖板交接处.

3 叶片疲劳寿命分析

3.1 雨流计数法统计计数结果

叶轮危险部位的应力曲线虽然整体呈周期性变化,但在具体应力值上仍存在很小的差值.由动力学分析得到的叶轮易产生疲劳破坏部位的应力-时间历程不能反映叶轮在寿命期内的载荷变化,也不能直接应用在疲劳分析中,因此需要采用统计学方法推断叶轮叶片在寿命期内所承受的应力变化规律.刘义伦[18]比较了各种计数法,认为雨流计数法可以记录载荷的起始点和中值以及应力的封闭环,能够提高疲劳寿命预测精度.因此,文中采用雨流计数法处理叶轮叶片易产生疲劳破坏部位监测点在10个旋转周期内的应力-时间历程数据,如图8所示,图中纵坐标N为循环次数.

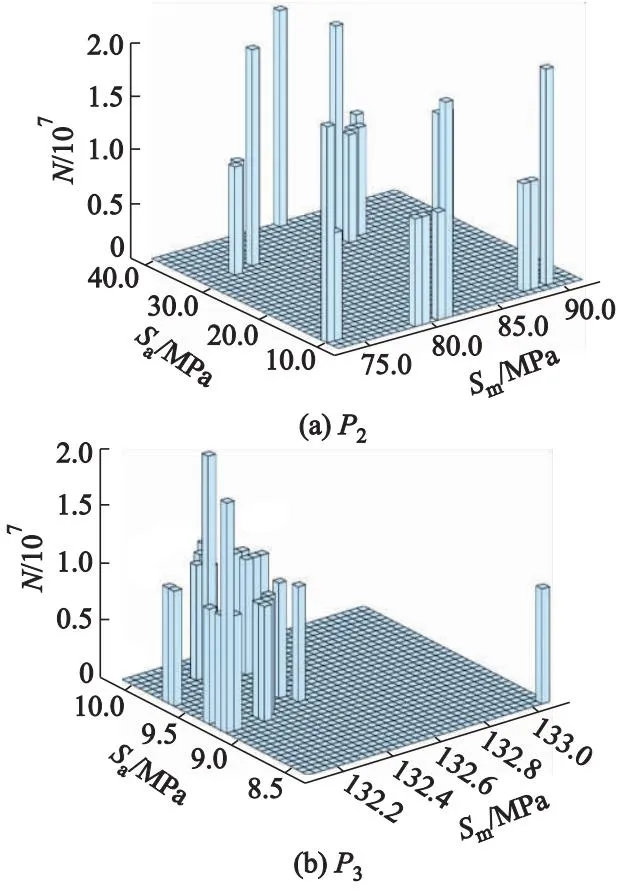
图8 危险点雨流计数法统计结果

3.2 疲劳计算参数的确定

材料的疲劳寿命曲线(S-N曲线)只代表加工精细的小尺寸试件的性能,实际零件表面光滑度、尺寸和形状各不一样,疲劳寿命分析须考虑这些因素对疲劳强度的影响[19].文中主要考虑4种因素,即应力集中、表面加工、结构尺寸和平均应力.其中,叶轮叶片危险部位即为应力集中部位,提取的应力数据为叶片危险部位的应力最大值,因此,不用进行应力集中的修正.表面加工和结构尺寸对材料疲劳寿命的影响可以采用修正系数进行修正[20].叶轮结构采用锻钢,对于叶轮叶片的结构尺寸,查得其尺寸系数ε=0.574 5,表面加工系数为β=0.567 8.平均应力对材料疲劳性能影响很大,利用Goodman直线[19,21]对雨流计数结果进行应力修正,将应力等寿命转换为对称循环(R=-1,Sm=0)下的应力水平,修正公式为

(1)

考虑各修正系数,则式(1)改为

(2)

式中:Sa(R=-1)为等寿命转换应力幅值.

3.3 S-N曲线

由于试验成本高,难以搭建高温高压试验台进行材料疲劳寿命试验.13Cr4Ni高温疲劳寿命曲线即S-N曲线采用最小二乘法拟合,查阅手册[20],拟合方程为

lgN=a+blgS,

(3)

式中:a,b为待定系数.

将N=1.0×103,S=0.90σb和N=1.0×107,S=0.45σb代入式(3),解得a=39.496 5,b=-13.287 7.

3.4 疲劳损伤计算

疲劳损伤本质是一个长期的积累过程,叶轮在10个旋转周期(0.405 4 s)内疲劳损伤是细微的.为了观察叶轮长时间受流体冲击的疲劳损伤程度,将危险部位10个周期雨流计数统计结果线性扩展绘制成1 000 h的载荷谱[21].疲劳损伤具体计算流程[19,21]:首先,基于雨流法计数结果,应用式(2)对各级应力幅值进行修正;其次,参照材料的S-N曲线,得到各级应力值下的疲劳循环次数Ni;然后,依据一段时间(0.405 4 s)与1 000 h之间的比例关系,求得各个应力值下的总循环次数ni;最后,计算各级应力循环造成的损伤di(di=ni/Ni),并进行累加,即可求得叶轮叶片的总疲劳损伤D.表2为设计流量工况下监测点P2处在1 000 h的疲劳载荷谱.

表2 监测点P2处1 000 h的疲劳载荷谱

依照上述方法,对设计流量工况下监测点P3进行疲劳总损伤计算,得到D=5.95×10-11.由此可见,监测点P2比P3的疲劳损伤高7个数量级,表明疲劳破坏会首先发生在叶片进口边与后盖板交接处,这与实际情况一致[9].

3.5 叶轮叶片疲劳寿命计算

根据线性疲劳累积损伤理论,叶轮叶片疲劳寿命和疲劳损伤关系[21]由式(4)表征,即

(4)

式中:L为叶片疲劳寿命;ΔT代表1 000 h.

根据式(4),计算得叶轮叶片的疲劳寿命为L=2 434 752.76 h,即277.94 a.

4 结 论

1) 对叶轮进行动应力分析可知,各危险点应力波动呈周期性,叶片进、出口边与前、后盖板交接处易产生应力集中,最大应力发生在叶片进口边与前盖板交接处,为142.57 MPa.

2) 对叶轮疲劳寿命进行分析可知,疲劳破坏首先发生在应力幅值最大的叶片进口边与后盖板交接处,而并非应力值最大部位.

3) 采用雨流计数法处理危险部位的动应力数据,据线性累积损伤理论编制1 000 h载荷谱,计算得到叶轮在设计流量工况下的疲劳寿命为277.94 a,验证了核主泵叶轮材料采用ASME 182 F6NM(13Cr4Ni)马氏体不锈钢的疲劳可靠性.