风向变化下不同材料叶片动态应力试验研究

汪建文,赵煜,张鹏,任彪,尹九俊

(1. 内蒙古工业大学能源与动力工程学院,内蒙古 呼和浩特 010051; 2. 内蒙古自治区风能太阳能利用机理及优化重点实验室,内蒙古 呼和浩特 010051; 3. 风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010051)

在“碳达峰,碳中和”的背景下,风力发电以其发电方式清洁、基建周期短等优点得到了国家的大力支持,风力机装机总量逐年提升.风力机工作于环境复杂多变的野外,自然风的大小及方向一直在发生变化,使得叶片的整个正常运行过程在各种复杂动态载荷作用下完成,叶片成为风力机上最容易受损的部件.风力机叶片抵抗载荷的能力越强,材料越轻,刚度和强度越高,叶片就可以做得越长,其捕风能力也就越强.所以研究风向变化下不同材料叶片载荷规律对风力机功率提升和安全稳定运行具有重要意义.

风力机叶片在运行过程中受到的载荷包括气动载荷、离心载荷、重力载荷和运行载荷等,对风力机叶片进行载荷分析显得尤为重要.目前,在风力机叶片应力特性研究方面,SANTO等[1]使用瞬态流固耦合仿真对风力机叶片进行了动态载荷和应力分析.BAQERSAD等[2]利用三维点跟踪和模态展开技术提取了任意激励下风力机叶片的全场动应变.FERNANDEZ等[3]介绍了一种可计算不同风况下风力机叶片整体和局部应力、应变结果的航空结构分析自动化程序.MENG等[4]采用基于应力的方法研究了不同尾迹条件下弯扭耦合效应引起的疲劳载荷.MOYNIHAN等[5]介绍了一种利用应变测量与数据采集计算运行中风力机叶片上应力和弯矩的方法.叶昭良等[6]基于CFD方法,对NREL Phase Ⅵ风力机进行了30°偏航角稳态和动态偏航气动特性模拟.白叶飞等[7]采用旋转机械应力应变无线遥测系统,对风力机叶片运行状态中的应力应变特性进行了试验研究.马剑龙等[8]对直径1.4 m的小型水平轴风力机风轮进行了振动频率及应力特性的试验研究.杜鹏程等[9]通过数值模拟对离心载荷作用下的叶片表面应力特性进行了研究.

风力机叶片所选材料不同,其各方面性能也会有所差异,当前用来制作叶片的主流材料有木材、玻璃纤维和碳纤维等.GUKENDRAN等[10]研究了4种不同类型的复合材料的性能,使用ANSYS Workbench对一种典型风力机叶片的变形、应变等进行了详细研究.YUAN等[11]研究了碳纳米管增强复合材料对不同风速下风力机叶片颤振行为的影响.WU等[12]对非定常气动载荷下黏合扩展复合材料风力机叶片的应变响应和疲劳寿命进行了研究.MUHAMMED等[13]使用ANSYS软件研究了复合材料在不同负载条件下对风力机叶片应用的适用性.张建平等[14]分析了碳纤维与玻璃钢材料的叶片在静止工况下的模态频率与振型,对比了2种叶片在额定工况下的应力与位移.马铁强等[15]基于连续介质损伤力学提出一种风力机叶片面内复合材料渐进损伤分析和预测的新方法.

从上述研究可知,关于风力机叶片载荷规律方面的研究,主要集中在单种材料叶片在风向不变情况下的数值模拟分析,对风向变化条件下不同材料叶片的载荷试验研究较少.当前,小型风力机叶片材料主要包括木质和玻璃纤维材料,少部分为全碳纤维制作,用于电动机转速较高的情况,能很好满足叶片质量轻且强度高的要求.因此,文中以木质、玻璃纤维和碳纤维材料的S型小型风力机叶片为研究对象,对3种材料叶片分别进行风向变化下的应力、应变试验研究,得到每种材料叶片在风向变化过程中的应力、应变变化规律并进行对比分析,旨在为不同材料小型风力机叶片在实际环境中的载荷分析、故障诊断等提供一定参考.

1 试验设备及方案

试验在内蒙古工业大学风能太阳能利用技术教育部重点实验室的直流式低速风洞开口段进行,风洞开口段直径2.0 m,所用风力机叶片为课题组自行设计的S型小型风力机叶片,翼型为SD2030翼型,风轮直径d=1.4 m,风轮旋转中心距离风洞开口中心0.5d,距地面高度h=1.7 m,额定风速v=8.0 m/s,额定尖速比λ=5.0,风轮圆周方向固定.S型小型风力机叶片展向各截面的形状参数如表1所示,表中R为半径,C为弦长,γ为安装角.

表1 叶展形状参数

试验所用叶片如图1所示,图中从左往右依次为木质叶片、玻璃纤维叶片和碳纤维叶片.

图1 3种材料风力机叶片

3种材料叶片的弹性模量E,泊松比μ和质量m如表2所示.

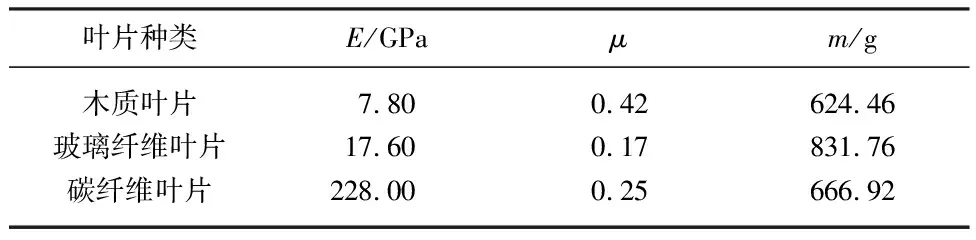
表2 3种材料叶片特性

由于风洞产生的来流风无法改变风向,所以使用安装在风力机塔筒底部的动态旋转平台带动风力机旋转,使风力机整机与来流风产生相对转速.

试验装置示意图如图2所示,首先对控制柜上的控制器进行编程,将控制器发出的信号传递至伺服电动机并使其转动,再由伺服电动机带动动态旋转平台及风力机整机按照设定好的转速转动至预设角度,与风洞产生的来流风共同模拟风向变化的过程.

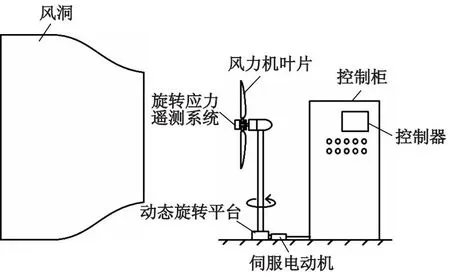
图2 试验装置示意图

试验装置如图3所示,图中从左往右依次为控制柜、伺服电动机、动态旋转平台和风力机整机.

图3 试验装置图

文中模拟的风向变化情况均为风轮平面由正对来流风的0°逆时针变化至45°的过程,模拟风向变化过程的俯视示意图如图4所示.

图4 模拟风向变化俯视示意图

试验中使用电测法测量叶片动态应变,由于叶片表面各位置处主应力的大小和方向都未知,所以需要测量同一测点处3个方向的应变,通过公式计算,才能确定主应力的大小和方向.故文中选择使用三轴应变花,测量测点处主应力的大小及方向.三轴应变花上的丝栅角度分别为0°,45°,90°,以测量测点处的3个方向的线应变,如图5所示.

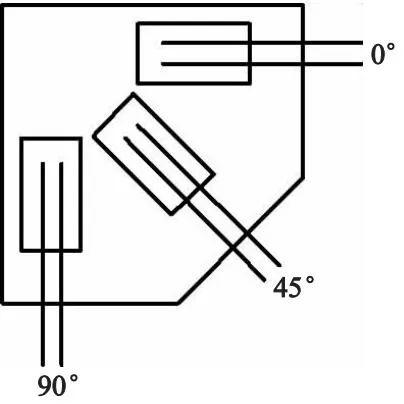
图5 三轴应变花示意图

由三轴应变花测得每一测点处3个方向的线应变数据后,通过DH5953G旋转信号采集仪将采集到的数据传输至DHDAS动态信号采集分析系统进行分析,该系统测试准确度为0.5%±3 μɛ.测试得到的主应变ε,主应力σ,最大主应力方位角θ的计算公式为

(1)

(2)

(3)

式中:ε0为0°方向线应变;ε45为45°方向线应变;ε90为90°方向线应变.

叶片在运行过程中主要受到气动载荷、重力载荷和离心载荷的作用.叶片单位长度截面受到的气动力为

(4)

(5)

式中:v为相对速度;ρ为空气密度;α为来流角;Cl为升力系数;Cd为阻力系数.

叶片单位长度的重力为

ρ0F0=∑ρiFi,

(6)

式中:ρ0为叶片截面折算密度;F0为叶片截面折算面积;ρi为每部分截面的密度;Fi为每部分截面面积.

离心载荷计算公式为

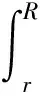
(7)

式中:Fz为离心力载荷;mi为每部分单位质量;ω为叶轮旋转角速度.

根据式(4)—(7)可知,在相同工况(同风速、同叶尖速比)下,由于3种材料叶片外形相同,受到的气动载荷一致,但3种材料叶片重量不同,重量较大的叶片受到的重力载荷和离心载荷较大,则相同测点处应变花3个方向线应变较大,由式(1)得知测点处的最大主应变较大;根据式(2)得知叶片的最大主应力受3个方向线应变、叶片材料弹性模量E和泊松比μ共同影响.

对叶片进行模态敲击试验,获得3种材料叶片的节线位置,考虑到以往课题组对木质叶片应力和应变规律研究较多,为与以往研究成果形成对照,选择以木质叶片的节线位置为依据进行应变花的布置.木质叶片的前三阶模态振型如图6所示.应变花布置位置示意图如图7所示.

图6 木质叶片低阶测试模态振型

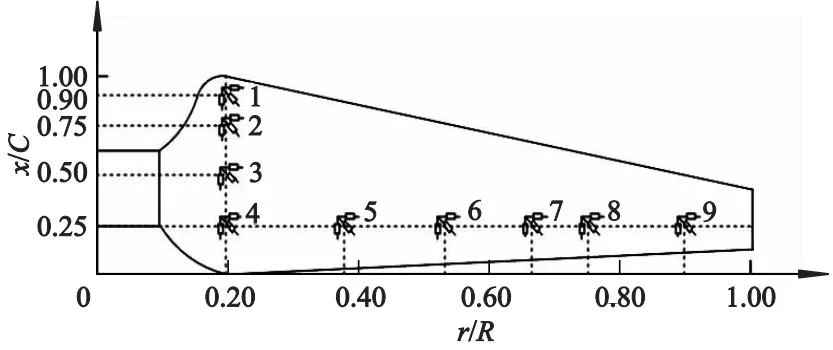
图7 应变花布置位置

由图6可得,木质叶片一阶振动节点在0.20R处,二阶振动节点出现在0.20R,0.75R处,三阶振动节点出现在0.20R,0.53R,0.90R处.结合叶片设计结构,选择在3种材料叶片压力面沿叶片展向距离叶根0.20R,0.39R,0.53R,0.67R,0.75R,0.90R与叶片展向气动中心线的交点位置,以及距离叶根0.20R处弦向0.90C,0.75C,0.50C,0.25C位置分别粘贴三轴应变花,对风向动态变化过程中叶片的应力、应变变化情况进行测量.

2 测试结果及分析

2.1 测试误差分析

在试验过程中,由于外部环境、人为因素和设备精度等问题使得试验结果往往存在误差.故在相同条件下分别对3种材料叶片进行试验,并对试验数据进行了相对误差分析,试验条件为风速8 m/s,叶尖速比为5.0,来流风向垂直于风轮平面,对测点4的最大主应力值每秒统计一次,重复5次.表3为碳纤维叶片不同组测点4实测最大主应力值σmax.

表3 碳纤维叶片不同组测点4实测最大主应力值

表4为不同组碳纤维叶片测点4最大主应力值相对误差δ.

表4 碳纤维叶片不同组测点4最大主应力值相对误差

由表4可知,碳纤维叶片试验数据的最大相对误差为4.711%,另外,木质、玻璃纤维叶片数据相对误差由于篇幅原因在此不再给出,其最大相对误差分别为-4.890%,4.942%,基本满足试验精度要求.

2.2 叶根弦向应力变化规律分析

选择额定工况即风速8 m/s,尖速比为5.0的条件下,对风向变化角以5°/s的角速度由0°变化至45°过程中叶根处的应力变化规律进行分析.3种材料叶片叶根处最大主应力变化曲线如图8所示,其中横坐标为时间,纵坐标为最大主应力值,每一时间的最大主应力值取该时间±0.5 s内的平均值.

图8 叶根处应力值随时间变化曲线

图8中,在t=5 s时,风向角开始以5°/s的角速度变化,当t=14 s时,风向角停止转动,此时风向角为45°.

由图8可知,在整个测量时间内,3种材料叶片根部应力分布有所差别,但应力值基本呈现由前缘(0.25C)向后缘(0.90C)递减的趋势,即靠近前缘位置处应力值较大,靠近后缘位置处应力值较小.风向动态变化过程中,即t=5～14 s内,各测点应力值均随时间的增加而减小,这是由于来流风速与翼型截面弦线的夹角逐渐增加,风轮扫风面积减小导致气动载荷减小,并且风轮转速随风向角的增加而逐渐减小导致离心载荷产生的展向拉伸减小,使得应力值下降.当t=14 s时,风向变化至45°并保持不变,此时气动载荷大小不再变化,但由于转动惯量继续释放,风轮转速会继续减小一段时间直至稳定,离心载荷产生的拉伸作用减小,应力值也随之减小一段时间直至稳定.当3种材料风力机叶片应力值在风向角为45°的情况下达到稳定时,叶根处各测点应力值趋于一致并接近于0.

2.3 叶片展向应力变化规律分析

当风速为8 m/s,尖速比为5.0时,风向角以每秒5°的角速度由0°变化至45°过程中3种材料叶片展向6个测点位置的最大主应力随时间的变化曲线如图9所示.

图9 叶片展向应力值随时间变化曲线

由图9可知,3种材料叶片展向的最大主应力值均呈现由叶根(0.20R)向叶尖(0.90R)逐渐递减的趋势, 即靠近叶根位置处应力值大,靠近叶尖位置处应力值小,这是由于S型叶片叶根处扭角及重量较大,在离心载荷及气动载荷二者耦合作用下,最大主应力的作用效果集中在叶根部位,使得不同材料S型风力机叶片叶根位置均为叶片最容易发生损坏的部位.

木质叶片和碳纤维叶片应力值由叶根向叶尖减小的程度较为均匀,而玻璃纤维叶片根部比叶片展向其他位置处的应力值有明显增幅,说明由于叶片材料不同,导致同翼型叶片表面的应力分布不同.风向变化开始后,由于来流风速与翼型截面弦线的夹角逐渐增加,风轮扫风面积减小并且风轮转速逐渐降低,气动载荷和离心载荷逐渐降低,3种材料叶片展向各位置应力值逐渐下降,下降趋势同叶根处应力值下降趋势相似,都呈反S型下降曲线.碳纤维叶片展向应力值最先出现明显下降趋势,之后依次为玻璃纤维叶片和木质叶片.

2.4 测点4综合分析

选择测点4进行分析主要有以下2个原因:① 最佳位置,测点4既是展向方向上的测点,又是弦向方向上的测点,是弦向与展向测点的交界处;② 应力变化规律,3种材料叶片表面应力值基本呈现由前缘向后缘,由叶根向叶尖减小的趋势,测点4作为叶根前缘处的测点,其应力值在叶片表面是较大的.

2.4.1 测点4应力值随时间变化规律

最大主应力随时间的变化曲线如图10所示.由图可知,碳纤维叶片测点4处应力值远大于木质、玻璃纤维叶片测点4处的应力值,这是由于碳纤维叶片的弹性模量值远大于其他2种材料叶片的弹性模量值,使碳纤维叶片发生一定弹性变形所需的应力也就越大,即在同风速、同尖速比的条件下,刚度较大的碳纤维叶片在气动载荷、离心载荷和重力载荷耦合作用下产生的弹性变形最小.木质叶片弹性模量最小,其刚度最小,所以其应力变化曲线的值最小.此试验结果印证了文献[14]中刚度较高的碳纤维叶片应力响应值相对较大的数值模拟结论.风向变化开始后,碳纤维叶片应力值在t=6 s左右时有明显下降的趋势,而玻璃纤维叶片和木质叶片分别在t=8 s和t=9 s左右时开始有明显下降趋势,说明叶片材料弹性模量值越大,其抵抗弹性变形的能力越大,气动载荷和离心载荷减小后,其应力值出现明显下降趋势的时间越早.

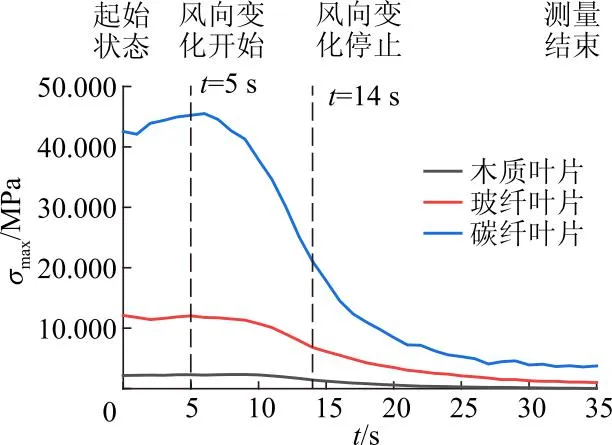
图10 3种材料叶片测点4应力值变化曲线

2.4.2 测点4应变值随时间变化规律

根据胡克定律σ=Eε可知,同一叶片同一位置处的应力值和应变值呈倍数关系,即应力值变化曲线和应变值变化曲线的变化规律一致. 文中3种材料叶片测点4应力值由大到小的顺序依次为碳纤维叶片、玻璃纤维叶片和木质叶片,但由于弹性模量E值的不同,使得3种材料叶片应变值从大到小的顺序会出现不同.

3种材料叶片测点4处最大主应变随时间的变化曲线如图11所示.

图11 3种材料叶片测点4应变值变化曲线

由图11可知,风向变化开始后,碳纤维叶片的应变值最先出现明显下降趋势,之后依次为玻璃纤维叶片和木质叶片.图中整个测量过程中,玻璃纤维叶片的应变值始终保持最大,这是由于在小型风力机正常运行过程中, 离心力对叶片表面动态应变影响的程度显著大于气动力,玻璃纤维叶片质量(831.76 g)比木质叶片质量(624.46 g),碳纤维叶片质量(666.92 g)分别大33.20%,24.72%,所以玻纤叶片重力载荷最大,并且在同风速、同尖速比的条件下,离心载荷产生的拉伸最大,其应变值也就最大.木质叶片与碳纤维叶片质量相近,相同风速及尖速比条件下的重力载荷、空气动力载荷和离心载荷较为接近,但碳纤维叶片比木质叶片刚度大,其抵抗弹性变形的能力比木质叶片强,所以碳纤维叶片的应变值最小.

由图10和图11可知,对于测点4,碳纤维叶片应力值虽然最大,但其在风向变化过程中的应变是最小的.风力机运行在风向变化的自然环境中时,叶片长期存在过大的应变会增加其断裂的风险,从叶片应变角度来说,碳纤维材料以其低应变性,比玻璃纤维和木质材料叶片更适用于电动机转速高的小型风力机上.

2.4.3 测点4的3个方向线应变变化规律

图12为3种材料叶片在风向变化过程中测点4的3个方向线应变随时间的变化曲线.

图12 测点4的3个方向线应变变化曲线

由式(1)可知,试验中测得的最大主应变值与弹性模量和泊松比无关,仅由应变花3个方向的线应变值决定,故应变花3个方向的线应变出现明显变化趋势的顺序依然为碳纤维叶片、玻璃纤维叶片和木质叶片.由图12可知,风向变化开始后,3种材料叶片测点4线应变的绝对值基本呈现随风向角增加而减小的趋势.

这是由于来流风速与翼型截面弦线的夹角逐渐增加,风轮扫风面积减小并且风轮转速逐渐降低,气动载荷,离心载荷逐渐降低,测点4处3个方向线应变的绝对值也减小;风向变化停止后,风轮转动惯量继续释放,3个方向应变值逐渐减小至稳定并接近于0.由测试结果可知,对于测点4,木质叶片和碳纤维叶片的0°线应变,玻纤叶片90°线应变值为正值,受到拉伸力作用;木质叶片45°和90°线应变,玻纤叶片0°和45°线应变,碳纤维叶片45°和90°线应变值为负值,受到挤压力的作用. 所以,对于同一翼型表面上同一测点位置,材料不同会导致测点3个方向应变值的大小和正负不同,即受到拉伸或挤压作用的效果的大小不同.

2.4.4 测点4最大主应力方位角变化规律

根据应变花的布置方向和接线方式,定义应变花水平方向为0°线,垂直于0°线上方的线段为-90°线,垂直于0°线下方的线段为90°线,最大主应力σmax与0°线的夹角θmax称为最大主应力方位角,单位为(°),可由公式(3)计算得到.当σmax位于0°线上方时,方位角为负值,指向叶片后缘;σmax位于0°线下方时,方位角为正值,指向叶片前缘.最大主应力方位角如图13所示.

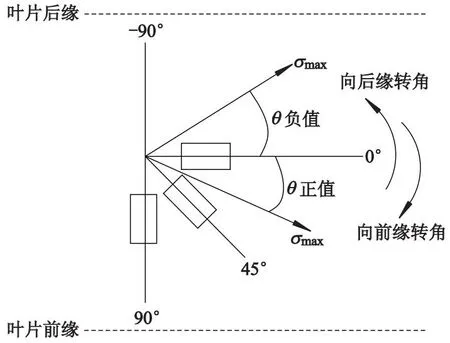
图13 最大主应力方位角

图14为3种材料叶片在风向变化过程中测点4最大主应力方位角随时间的变化曲线.

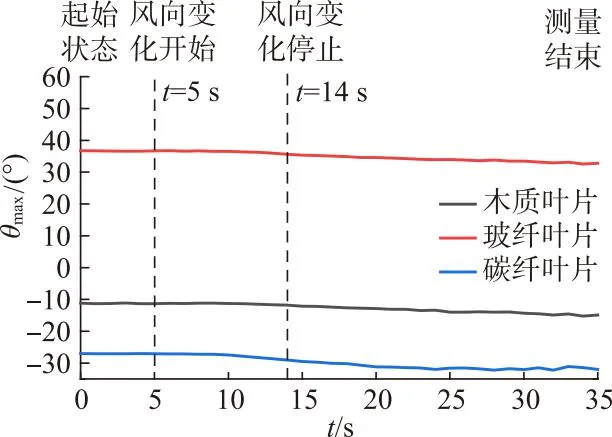
图14 测点4最大主应力方位角随时间变化曲线

由图14可知,当风向变化角速度为每秒5°时,整个测量过程中最大主应力方位角的值较为稳定,3种材料叶片测点4的最大主应力方位角仅在风向变化开始一段时间后有略微减小的趋势.木质叶片和碳纤维叶片最大主应力方位角为负值,位于0°线上方,说明最大主应力作用方向为指向叶片后缘,这是由于在图12中,木质叶片和碳纤维叶片测点4应变花0°方向线应变最大,使得方位角向后缘转角、玻璃纤维叶片最大主应力方位角为正值,位于0°线下方,说明最大主应力方向指向叶片前缘,同理,由于玻纤叶片测点4应变花90°方向线应变最大,使方位角向前缘转角.由此可知,对于同一翼型表面的同一测点,叶片材料不同会导致最大主应力方位角产生较大差异.

3 结 论

1) 3种材料叶片展向和叶根弦向应力分布有所差异,但总体基本呈现由前缘向后缘,叶根向叶尖递减的趋势.风向变化开始后,各材料叶片测点处应力值均逐渐减小,风向变化至45°且稳定不变后,应力值继续随转速的减小而减小,直至稳定并接近于0.应力值随时间减小的趋势呈反S型曲线.

2) 同风速、同尖速比条件下弹性模量较大的碳纤维叶片叶根前缘处应力值远大于玻璃纤维,木质叶片叶根前缘处的应力值.重量较大的玻璃纤维叶片重力载荷及离心载荷大于木质和碳纤维叶片,其叶根前缘处应变值最大,而碳纤维叶片叶根前缘处应变值最小.

3) 风向变化开始后,刚度较高的碳纤维叶片叶根及展向应力,应变值最先出现明显下降的趋势,之后依次为玻璃纤维叶片和木质叶片.

4) 同一翼型表面上同一测点位置,材料不同会导致测点3个方向线应变的大小和正负不同,即受到拉伸和挤压作用的效果大小不同.

5) 相同翼型表面的同一测点,叶片材料不同会导致最大主应力方位角产生较大差异.