基于变分模态分解和集成学习的光伏发电预测

邱书琦，蹇照民，方立雄，秦婧雯，万俊岭，袁培森

（1.国网新疆电力有限公司营销服务中心，新疆乌鲁木齐 830000；2.南京农业大学人工智能学院，江苏南京 210095）

0 引言

分布式光伏具有投资小、清洁保护及供电可靠等优点，当前大规模的光伏发电系统作为清洁能源发展迅速[1]。而光伏发电易受到气象及其他因素的影响，因此产生的随机性、间歇性与波动性对电力系统的经济、安全与可靠运行造成了很大困扰[2]。研究表明光伏并网发电容量大于电力系统总发电量的15%后，光伏并网发电的波动性将引起电力系统崩溃[3-4]。因此实现光伏发电量的准确预测对电网调度及光伏电站运行具有重要意义[5]。

近年来，研究者使用变分模态分解（Variational Mode Decomposition，VMD）方法研究电力负荷信号的分解[6]。俞敏等[7]采用VMD 方法将光伏功率序列分解成不同频率的子模态，通过皮尔逊相关性分析确定影响各模态的关键气象因子。商立群等[8]利用VMD 方法对非平稳的光伏发电功率序列进行平稳化处理，得到若干个规律性较强的子序列，减小在分解预测重构时的误差，具有更好的适应性和分解效果。由于分解模态个数K和带宽限制α的选取对VMD 方法的分解效果影响很大，使用寻优算法能快速选择合适的参数组合，文献[9-10]使用了参数寻优算法来改进VMD。VMD 与其他数据处理方法相结合往往能提高光伏数据集的处理效果，文献[11-12]使用了特征选择和VMD 的组合数据处理方法，能够得到更可靠的光伏发电功率预测结果。

集成学习算法可分为Bagging[13]，Boosting[14]和Stacking[15]3 种：Stacking 通常考虑异构弱学习器，而Bagging 和Boosting 通常考虑同构弱学习器；Stacking 使用元模型组合基模型，而Bagging 和Boosting 按照确定性算法组合弱学习器。杨荣新等[16]以极端梯度提升（Extreme Gradient Boosting，XGBoost）[14]、轻度梯度提升机（Light Gradient Boosting Machine，LigtGBM）[17]、随机森林（Random Forest，RF）[18]3 种机器学习算法作为Stacking 集成学习的第1 层个体学习器，以线性回归作为第2 层元学习器，提出了1 种基于Stacking 集成学习的光伏发电量预测方法，相较于单一的机器学习模型，提升了预测精度。崔树银等[19]提出了1 种在Stacking集成学习框架下融合Bagging 和Boosting 算法的短期光伏功率预测模型，结果表明Stacking 模型相较于单一模型有着更小的误差和更高的预测精度。

综上所述，针对当前光伏发电量预测方法发电量数据的分解效果不好、单一模型的预测准确率提升有限以及相关研究较少等问题，本文基于贪心算法选择模态分量改进了VMD，结合特征选择、改进VMD 和集成学习技术提出了1 种基于改进VMD 和集成学习的光伏发电量预测方法。通过特征选择去除不相关或冗余特征获得光伏特征子集，使用基于贪心算法的模态分量子集选择方法来改进VMD，选择预测表现最好的模态分量参与光伏发电量预测，提高预测的准确度；借助集成学习方法将几个简单的模型集成起来构造发电量分量子集预测模型，从而实现对光伏发电量的准确预测。

1 光伏发电量预测

1.1 预测过程

本文采用基于改进VMD 和集成学习的预测方法进行光伏发电量预测。预测流程如图1 所示，包括以下5 个步骤：

图1 基于VMD和集成学习的光伏发电量预测流程图Fig.1 Flow chart of photovoltaic power generation prediction based on VMD and ensemble learning

1）使用极端随机树（Extremely Randomized Trees，ERT）进行特征选择，得到光伏特征子集。极端随机树方法是基于随机特征点进行划分的方法，其最终得到的决策树泛化能力强于RF[20]。

2）采用VMD 方法分解光伏发电量数据，得到K个模态分量（Intrinsic Mode Functions，IMF）和原始残差。

3）使用贪心算法进行IMF 分量选择，被选中的IMF 分量i，j，k等组成IMF 子集，计算新残差。

4）在光伏特征子集上分别训练用于预测IMF子集和新残差的Stacking 模型。

5）将测试集的光伏特征子集分别输入Stacking模型，得到IMF 子集和新残差的预测结果。把预测结果得到的各个分量的预测结果进行组合叠加，重构后得到光伏发电量的最终预测结果。

1.2 预测算法

1.2.1 改进VMD

VMD 是一种能够将多分量信号一次性分解成多个单分量调幅调频信号的时频分析方法[21]。VMD方法在获取固有分量IMF 时，将信号的分解引入到变分模型中进行解决，利用寻找约束变分模型最优解的过程进而实现信号的分解[22]。其分解过程最终转化为求变分问题的最优解过程。

本文使用VMD 算法进行光伏发电量数据分解，算法的输入是原始光伏发电量序列，输出{uk} 表示分解得到的发电量IMF 分量的集合，uk为调幅调频信号。算法的步骤为：（1）首先初始化第k个IMF分量的uk，第k个IMF 分量的瞬时频率ωk和拉格朗日乘数λ，令迭代次数n=0；（2）n=n+1，对所有频率ω≥0，从k=1 开始根据式（1）和式（2）更新uk和ωk；（3）每更新一次k自增1，直到k=K，再根据式（3）更新λ，直至满足式（4），停止迭代，否则转到步骤2）继续执行分解；（4）返回{uk} 。

式（1）—式（3）分别为uk，ωk和λ的更新函数，式（4）是VMD 算法的迭代约束条件。

式中：τ为噪声容忍度；ε为精度。

贪心算法是一种解决最优化问题的简单策略[23]，它通过逐步局部最优化求解，实现全局最优。

本文使用贪心算法进行IMF 分量选择。算法的输入Q表示IMF 分量候选集合，输出S表示选择的IMF 子集，S0是用来暂存未扩展S的临时变量。算法的步骤为：（1）首先初始化S和S0为空；（2）然后用S0暂存当前S，从Q中选择最大决定系数对应的IMF 分量q作为候选分量，尝试把q加入S；（3）从Q中删除q，比较使用加入q后的分量子集S和未加入q的分量子集S0进行发电量预测的决定系数大小；（4）如果S对应的决定系数反而小于S0，说明q并不参与构成最优解，从S中删除q；（5）重复执行步骤（2）—（4）直到Q为空，返回IMF 子集S。

1.2.2 Stacking集成学习

Stacking 方法[24-25]中有2 个阶段的模型：第1 个阶段是以原始训练集为输入的模型，称为基模型；第2 个阶段是以基模型在原始训练集上的预测作为训练集，以基模型在原始测试集上的预测作为测试集的模型，称为元模型。

本文Stacking 方法的流程图如图2 所示。

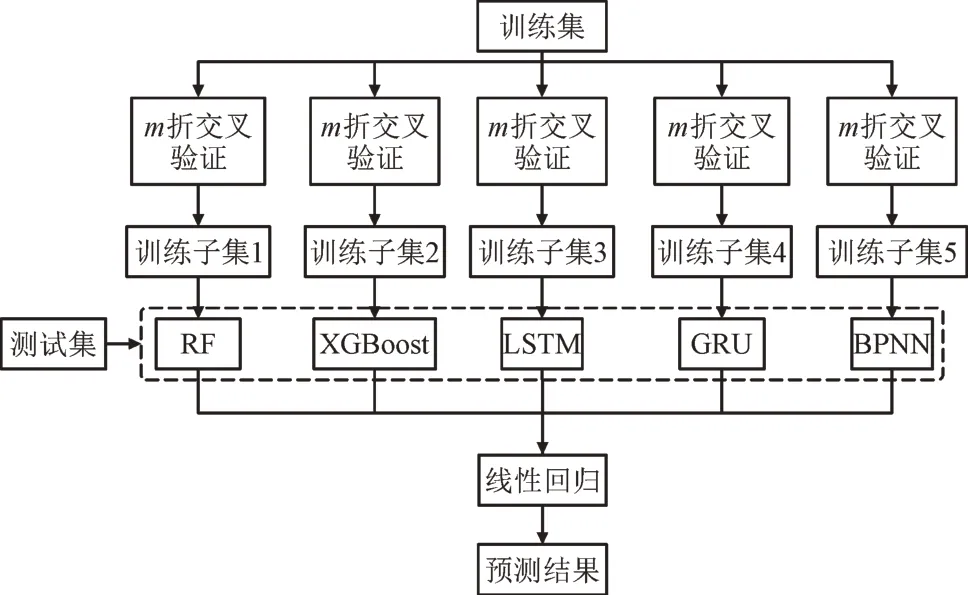
图2 基于RF，XGBoost，LSTM，BPNN和GRU的Stacking算法流程图Fig.2 Flow chart of Stacking algorithm based on RF，XGBoost，LSTM，BPNN and GRU

首先通过m折交叉验证构造训练子集，分别构造RF，XGBoost，长短期记忆网络（Long Short-term Memory，LSTM）、反向传播神经网络（Back Propagation Neural Network，BPNN）、门控循环单元（Gated Recurrent Unit，GRU）共5 种模型作为个体学习器；然后使用训练子集训练这些个体学习器得到基模型，再构造线性回归模型作为元学习器，使用这些基模型的输出训练元学习器。在测试集测试时，先使用基模型进行预测生成新的测试集，再对测试集进行预测。

光伏数据集是1 个时间序列，因此使用时间序列交叉验证法[26]划分数据集。光伏数据集的划分如图3 所示。

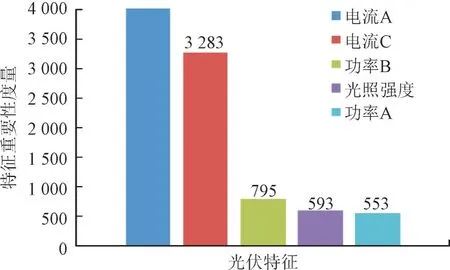
图3 按特征重要程度降序排序的前5个光伏特征Fig.3 Top 5 Photovoltaic characteristics in descending order by feature importance

根据式（5）将数据集D划分为m个大小相似的互斥子集，假设前h折数据为训练集，第h+1 折数据为验证集，返回的训练集索引和验证集索引分别是{1,2,…,h}和h+1。

式中：Dh为第h个数据子集。

2 实验结果及分析

2.1 实验平台及数据集

本文的实验环境为macOS Monterey12.6，CPU为Apple M2，内存16G，GPU 为Apple M2。算法基于Scikit-learn 1.2.1，Tensorflow 2.9.1 使用Python 3.9 实现。本文数据集来自https://www.datafountain.cn/competitions/303/datasets，该数据集包含21 个特征，包括ID、板温、光照强度、发电量等共9 000 条数据。本文按照8:2 将数据集划分为训练集和测试集。

2.2 结果评价指标

本文采用决定系数R、均方误差（Mean Square Error，MSE）（量值为EMS）、平均绝对误差（Mean Absolute Error，MAE）（量值为EMA）等作为评价指标，衡量模型对光伏发电量预测的效果。

决定系数用于评估预测值和真实值的符合程度，其计算如式（6）：

式中：t为样本数量；ye为第e个样本的真实值；为第e个样本的预测值；为所有样本真实值的平均值。

均方误差用于计算预测值和真实值之间差平方的平均值，其计算如式（7）：

平均绝对误差用于计算真实值与预测值之间绝对差的平均值，其计算如式（8）：

一般决定系数越接近1、均方误差和平均绝对误差越小表示回归分析中自变量对因变量的解释越好。

2.3 特征选择

本文构造Extra-Trees 模型[20]用于评估特征的重要性。以MSE 作为特征重要性评分的依据，MSE越小特征重要程度越高，在训练集上拟合Extra-Trees 模型，获取被选中的特征。光伏数据集19 个特征按特征重要程度排序的前5 个特征见图3。由图3 可知，光伏数据集特征重要程度前5 个特征分别是光照强度、电流A、电流C、功率A、功率B，因此选择这5 个特征组成光伏特征子集。其中电流A为采集点a处汇流箱电流值，电流C 为采集点c处汇流箱电流值，功率A 为采集点a处的功率Pa，功率B 为采集点b处的功率Pb。

2.4 变分模态分解参数优化

本文使用粒子群优化算法（Particle Swarm Optimization，PSO）[27-28]确定VMD 的分解模态个数K和带宽限制α。PSO 算法迭代的全局最优适应度曲线如图4 所示。

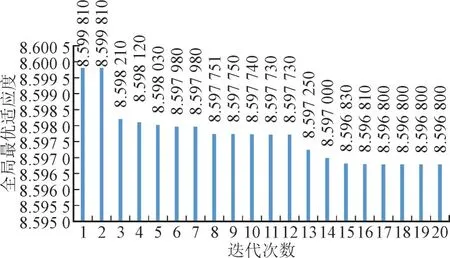
图4 PSO算法迭代的全局最优适应度曲线Fig.4 Global optimal fitness curves for PSO algorithm

由图4 可知，从第18 次迭代开始，上一次迭代后全局最优适应度与本次迭代后全局最优适应度之差小于1×10-6，全局最优适应度保持稳定。此时对应的分解模态个数K和带宽限制α分别是5 和8 009，因此分解模态个数K和带宽限制α的最佳参数组合是5 和8 009。

2.5 IMF子集选择

VMD 分解得到的5 个IMF 分量对应的预测模型决定系数如表1 所示，候选集Q是{IMF0，IMF1，IMF2，IMF3，IMF4}，其中IMFi表示第i个IMF 分量[29]。IMF2 的决定系数最大，因此第一个加入IMF子集S的为IMF2。

表1 VMD分解的IMF分量预测模型决定系数Table 1 Determinant coefficient for IMF component prediction model by VMD

IMF 子集S扩展过程中所有候选S的预测模型决定系数R2如图5 所示。使用贪心算法选择IMF子集，得出最终S为{IMF2，IMF3，IMF4}。

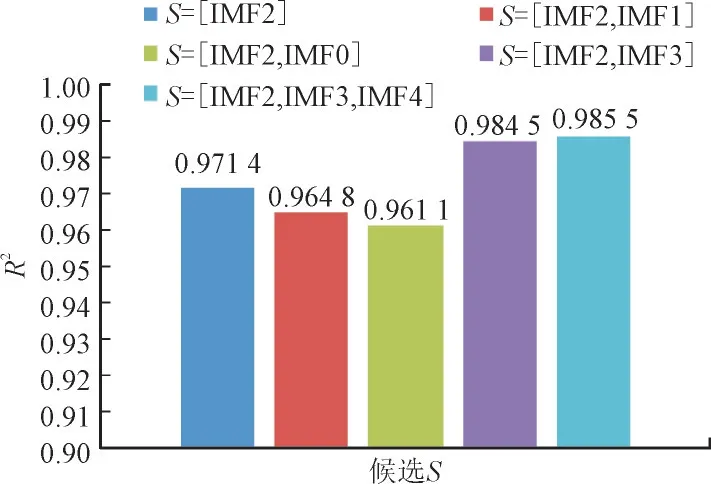
图5 VMD分解的IMF子集S上预测模型的决定系数Fig.5 Determinant coefficient for IMF subsets of S prediction model by VMD

由图5 可知，当IMF 子集S为{IMF2，IMF3，IMF4}时，预测模型的决定系数最大。因此，最终IMF 子集为{IMF2，IMF3，IMF4}。

2.6 预测结果对比分析

本文在特征选择、改进VMD 基础上采用Stacking 集成学习方法进行光伏发电量的预测，并将本文方法与基学习器、VIS 算法、其他几种分解方法和不进行分解的方法进行对比。比较指标包括EMS，EMA和R2。

下文中，VIS 表示改进变分模态分解和Stacking集成学习的组合预测方法，其与本文方法的不同之处在于使用全部特征参与预测；FEIS 表示特征选择、改进经验模态分解（Empirical Mode Decomposition，EMD）和Stacking 集成学习的组合预测方法，其与本文方法的不同之处在于使用改进EMD 方法分解光伏发电量数据；FVS 表示特征选择、VMD 和Stacking集成学习的组合预测方法，其与本文方法的不同之处在于使用未改进的VMD 方法分解光伏发电量数据；FES 表示特征选择、EMD 和Stacking 集成学习的组合预测方法，其与本文方法的不同之处在于使用未改进的EMD 方法分解光伏发电量数据；FS 表示特征选择和Stacking 集成学习的组合预测方法。

本文使用均方误差MSE、平均绝对误差MAE、决定系数R2评估算法的预测效果。

2.6.1 与基学习器预测结果的对比与分析

采用本文方法以及基学习器RF，XGBoost，LSTM，BPNN 神经网络、GRU 算法对光伏发电量进行预测，测试集上算法的MSE，MAE，R2值如表2 所示。

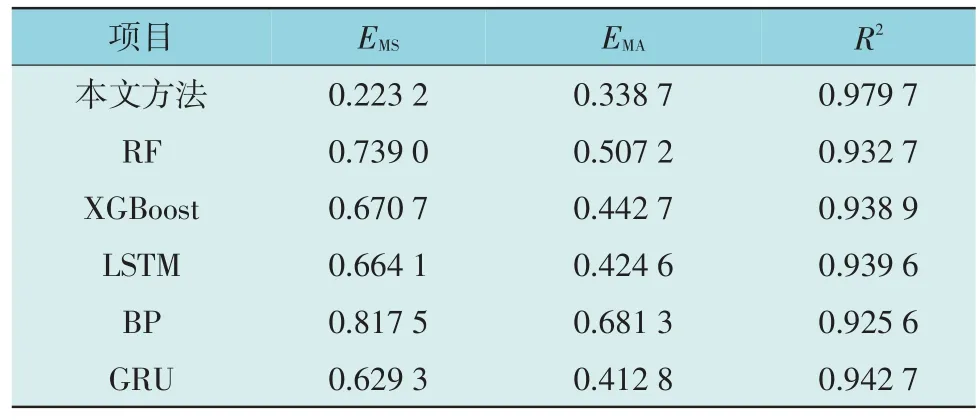
表2 本文方法与基学习器的预测结果对比Table 2 Comparison of prediction results between the proposed method and base learners

由表2 可知，本文方法相较RF，XGBoost，LSTM，BP，GRU 的均方误差值分别下降了69.80%，66.72%，66.39%，72.70%，64.53%；平均绝对误差值分别下降了33.22%，23.49%，20.23%，50.29%，17.95%；决定系数值分别上升了5.04%，4.35%，4.27%，5.84%，3.92%。

2.6.2 与特征选择预测结果的对比与分析

本文方法与VIS 算法在测试集第1 000～1 050条数据上预测结果与真实值的拟合图像如图6 所示。图6 中用序号0 表示第1 000 条数据，50 表示第1 050 条数据。从图6 可以看出，本文方法与VIS 算法的预测结果都能与真实值较好地拟合，但本文方法比VIS 算法拟合效果更好。

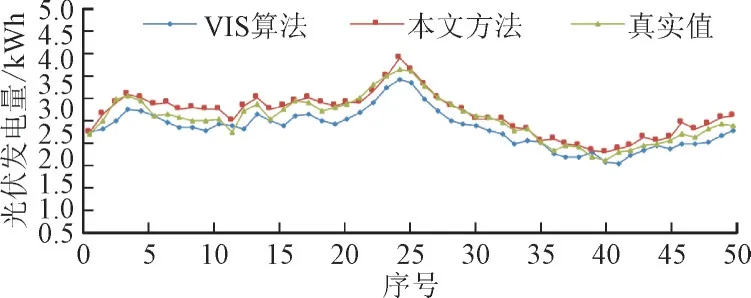
图6 本文方法与VIS算法预测结果与真实值的拟合曲线Fig.6 Fitting curves between predicted result and real value with the proposed method and VIS algorithm

采用本文方法与VIS 算法对光伏发电量进行预测，测试集上算法的MSE，MAE，R2及运行时间如表3 所示。

表3 本文方法与VIS算法的预测结果对比Table 3 Comparison of prediction results between the proposed method and VIS

由表3 可知，本文方法相较与VIS 的均方误差值下降了2.36%，平均绝对误差值上升了7.73%，决定系数值上升了0.05%，计算性能提升18.87%。

2.6.3 不同分解方法预测结果的对比与分析

采用本文方法以及FEIS，FVS，FES，FS 算法对光伏发电量进行预测，测试集上算法的MSE，MAE、R2值及运行时间如表4 所示。

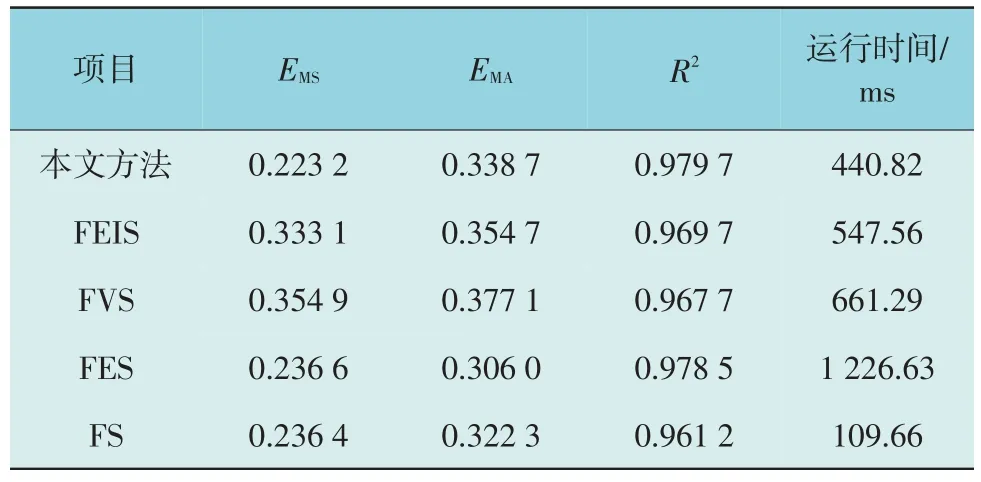
表4 本文方法与其他分解方法的预测结果对比Table 4 Comparison of prediction results between the proposed method and different decomposition methods

由表4 可知，本文方法相较FEIS，FVS，FES，FS的均方误差值分别下降了32.99%，37.11%，5.66%，5.83%；本文方法相较FEIS 和FVS 的平均绝对误差值分别下降了4.51%，10.18%，相较FES 和FS 的平均绝对误差值分别上升了10.69%，5.09%；本文方法相较FEIS，FVS，FES，FS 的决定系数值分别提升了1.03%，1.24%，0.12%，1.92%；文方法相较FEIS，FVS，FES 的计算速度分别提升了19.50%，33.34%，64.06%。

综上所述，本文方法在测试集上的MSE 最小，R2最大，且计算速度快，对光伏发电量预测具有好的效果。

3 结语

本文提出了基于改进VMD 和集成学习的光伏发电量预测方法。通过改进VMD 方法分解光伏发电量数据，得到发电量分量，使用集成学习方法构建模型预测发电量分量，再将发电量分量的预测值进行组合进行预测。实验结果表明了本文方法可提高光伏发电预测的准确性和稳定性，且有更快的计算速度。