电网电压不平衡下六边形变换器的微分平坦控制策略

程启明，沈治超，王为涛，罗力珲，张 梁，渠博岗

（上海市电站自动化技术重点实验室（上海电力大学自动化工程学院），上海 200090）

0 引言

随着“双碳”计划的提出，人们逐渐将目光投向于具有环保性、可再生性和经济性等优势的海上风电中[1-2]。其中，低频交流输电（Low Frequency Alternating Current，LFAC）技术，相比于其他输电技术，只需使用一个陆上AC/AC 变换器就可实现，显著的降低了成本[3-5]。目前适用于海上风电的AC/AC 变换器主要有模块化多电平变换器（Modular Multilevel Converter，MMC）[6]、模块化多电平矩阵变换器（Modular Multilevel Matrix Converter，M3C）和六边形变换器（Hexagon Converter，Hexverter）等[7]。其中六边形变换器（Hexverter）在M3C 的基础上电压传输比突破了0.866 的限制[8-9]，提高了功率和电压等级[10]，将桥臂数量从9 个减少到了6 个，削弱了系统的耦合电平程度，且拓扑结构只有1 个循环电流路径，设备的体积和建设成本显著降低[11]，使其在众多AC/AC 变换器中脱颖而出。

文献[11]中首次提出了六边形的拓扑结构，并建立起桥臂电流电压的数学模型，但并未验证六边形变换器相比于其他变换器的功能性。文献[12]采用磁耦合支路电感器改进六边形变换器，并运用实例验证了耦合支路电感的六边形变换器的功能性，但并未对桥臂功率和子模块功率进行控制，控制效果需进一步提升。文献[13]虽根据六边形变换器的桥臂数学模型，提出了一种适用于所有工作点的桥臂能量控制方法，但控制难度和开关损耗较高。文献[14]提出了一种基于最优零线电压和环流的策略，将电容电压限制在特定范围内的同时将开关损耗降至最低，但未考虑电网电压不平衡下的所面临的控制问题。文献[15]首次将六边形变换器通过LFAC 应用于海上风电并网的控制方案，并引入双dq变换推导了六边形变换器的频率解耦数学模型，验证了六边形变换器的可行性与有效性，但该控制需要调节多组PID（Proportional-Integral-Derivative）控制器调节器，参数难以整定。文献[16]根据六边形变换器的各支路电压和功率间的关系，提出了一种新型电池荷电状态（State of Charge，SOC）平衡控制方法。

目前Hexverter 变换器的控制策略多停留于线性PID 控制，该控制方法结构简单、适应性强且易于实现[17-18]，但对于Hexverter 变换器自身的非线性特性，控制效果并不理想。且文献[11-16]都是针对Hexverter 在电网电压平衡状态下进行分析研究，而实际系统中电网三相电压常处于不平衡状态。电网不平衡的负序分量会导致Hexverter 产生谐波电压，加重了电网的不平衡程度[19]。

为解决Hexverter 变换器采用PID 控制和在三相电压不平衡中所遇到的问题，本文将微分平坦控制策略（Differential Flattenting Control，DFC）运用到了Hexverter 中。微分平坦控制相较于PID 控制，对系统的外来扰动具有较好的鲁棒性，且结构简单、易于实现[20-21]。首先，本文对Hexverter 的拓朴结构和工作原理进行介绍并推导出其数学模型。随后分析了Hexverter 的平坦性与稳定性，提出了微分平坦控制策略，并介绍了电网电压不平衡下的控制目标。最后在Matlab 和RT-LAB 实验平台中搭建Hexverter 的双侧DFC 控制和双侧PID 控制，并通过3 种不同工况下的模拟实验，来证明DFC 控制策略的先进性与正确性。

1 Hexverter的电路建模与数学模型

1.1 Hexverter的拓扑结构

Hexverter 的拓扑如图1 所示，其由6 个桥臂组成，每个桥臂均由n个子模块（sub-modular，SM），一个等效电阻R和一个电感L串联而成。每个子模块由一个H 全桥和一个直流电容C并联而成。当Hexverter 投入工作中时，可以根据不同的电压和功率需求调整子模块的数量，使得桥臂得到相应的电压需求。因此可将桥臂上的子模块等效为受控电压源，其等效电压为ubk，桥臂电流为ibk（其中k=1，2，…，6），循环电流为icir，2 个端口中性点分别为N，O，uNO为N点相对O点的中性点偏移电压差。

Hexverter 系统由U，V，W和A，B，C6 个端点引出u，v，w 和a，b，c 2 种不同频的三相交流连接端口，其中频率为fs的低频侧三相端口电压和电流分别为uu，uv，uw和iu，iv，iw；频率为fl的工频侧三相端口电压和电流为ua，ub，uc和ia，ib，ic。其中，低、工频侧频率可取为fs=50/3 Hz，fl=50 Hz。

1.2 Hexverter的数学模型

根据图1 中Hexverter 的拓扑结构，由基尔霍夫定理可以得到Hexverter 端口电压和桥臂电流为：

式中：t为单位时间。

环流电流为：

由式（1）—式（3）可知，6 个桥臂的电压电流分量与2 种不同频率的交流分量相互耦合并通过电路的连接相互影响，直接控制难以实现。因此，为方便推导，将1，3，5 桥臂定义为组1（用下标“1”表示），将2、4、6 桥臂定义为组2（用下标“2”表示），然后分别对2 组进行坐标变换，可得dq坐标系下的数学模型为:

式中：ubsdi，ubsqi和ubldi，ublqi（i=1，2）分别为低频侧、工频侧不同组桥臂在d，q轴上的分量；usd，usq和uld，ulq分别为低、工频侧端口电压在d，q轴上的分量；isd，isq和ild，ilq分别为低、工频侧端口电流在d，q轴上的分量；ωs，ωl分别为低频侧、工频侧的角频率。

2 Hexverter的控制策略

2.1 Hexverter桥臂的微分平坦控制策略

基于微分平坦理论设计的控制器结构简单、易于实现[22]，相比于传统PID 控制，DFC 控制对系统参数变化和外来摄动具有鲁棒性较强、超调及振荡现象较小等特点[23-24]。其基本原理如下：

设非线性系统为：

式中：x为状态变量矩阵；y为输出变量矩阵；u为输入变量矩阵；Rn为n维状态变量；Rm为m维输入；变量上方的“·”为变量的1 阶求导。

若x，y，u满足式（10），则该非线性系统满足微分平坦理论。

式中：α，β分别为状态变量、输入变量的微分阶数。

微分平坦控制系统框图如图2 所示。图2 中，yref为期望输出，uref.c为前馈控制生成的期望值，uref.b为误差模型生成的期望值，uref为最终输入控制量期望值，Δy为误差反馈值，Δyref为误差反馈设定值。

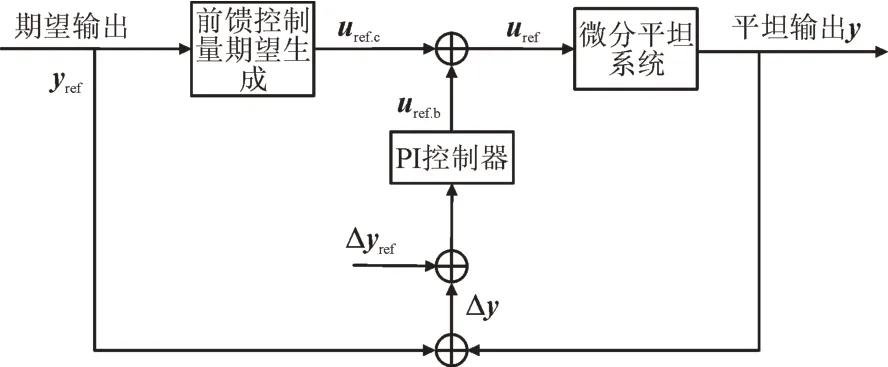
图2 微分平坦控制结构图Fig.2 Structure diagram for DFC

2.1.1 Hexverter的平坦性证明

为了方便后续推导，记：

由于Hexverter 变换器具有对称性，因此本文以低频侧时的y和u为例进行推导计算。在低频侧以式（5）为例可得输入变量为：

状态变量为：

由式（12）和式（13）可以看出，系统输入变量和状态变量可由输出变量y及其1 阶导数y˙表示，说明该系统满足微分平坦性。

2.1.2 微分平坦控制器设计

根据2.1 节所述的的控制原理，以第1 组桥臂的低频侧控制为例，根据式（5）可得DFC 控制器的前馈参考输入控制量为：

式中：ubsdref1.c和ubsqref1.c分别为第1 组桥臂的低频侧前馈参考输入控制量在d，q轴上的期望值；isdref和isqref分别为低频侧端口电流在d，q轴上的期望值。

令系统状态误差为：

式中：Δisd和Δisq分别为低频侧端口电流在d，q轴上的误差反馈值。

将式（15）带入到式（5）中可得误差反馈补偿值为：

式中：Δubsdref.b和Δubsqref.b分别为第1 组桥臂的低频侧误差模型生成的控制量在d，q轴上的期望值；Δisdref和Δisqref分别为低频侧端口电流在d，q轴上误差反馈设定值；Krefsp，Krefsi分别为低频侧DFC 控制器的PI 控制的比例系数、积分系数；s为拉普拉斯算子。

为了消除误差，令：

于是微分平坦控制的参考输入控制量为：

式中：ubsdref1和ubsqref1分别为第1 组桥臂的低频侧参考输入控制量在d，q轴上的期望值。

2.2 电压不平衡工况下Hexverter控制策略

电网电压不平衡是低频输电的常见问题[25]。为保证Hexverter 系统在不平衡工况下仍能正常运行，在DFC 控制的基础上进行了正负序分离操作，得到了DFC 的不平衡控制策略。以低频侧为例，在不平衡状态下Hexverter 的功率可表示为：

式中：Ps，Qs分别为有功和无功功率的总功率；Ps0，Qs0分别为有功和无功功率的直流量；Ps2sin，Qs2sin分别为有功和无功功率的2 倍频的正弦幅值；Ps2cos，Qs2cos分别为有功和无功功率的2 倍频的余弦幅值。

将式（19）写成矩阵形式可表示为：

式中：usd+，usq+，usd-，usq-和isd+，isq+，isd-，isq-分别为低频侧电压和电流在dq坐标系下的正、负序分量。

由于式（20）中6 个被控变量对应4 个控制变量，因此需根据不同电网需求选择被控目标。本文将控制目标分为以下3 种。

1）平衡电网电流

该控制目的在于平衡三相电网电流，使负序电流均为0。公式如下：

式中：i+sdref为d轴电流正序分量期望值；i+sqref为q轴电流正序分离期望值；i-sdref为d轴电流负序分量期望值；i-sqref为q轴电流负序分离期望值。

2）消除有功功率纹波

该控制目的在于消除有功功率的2 倍频分量，其公式如下：

3）消除无功功率纹波

该控制目的在于消除无功功率的2 倍频分量，其公式如下：

电网电压不平衡下Hexverter 系统的总控制框图如图3 所示。图3 中，Psref和Qsref分别为低频侧有功功率和无功功率的给定值，Plref和Qlref分别为低工频侧有功功率和无功功率的给定值，uuvw和iuvw为低频侧电压与电流值，uabc和iabc为工频侧电压与电流值。

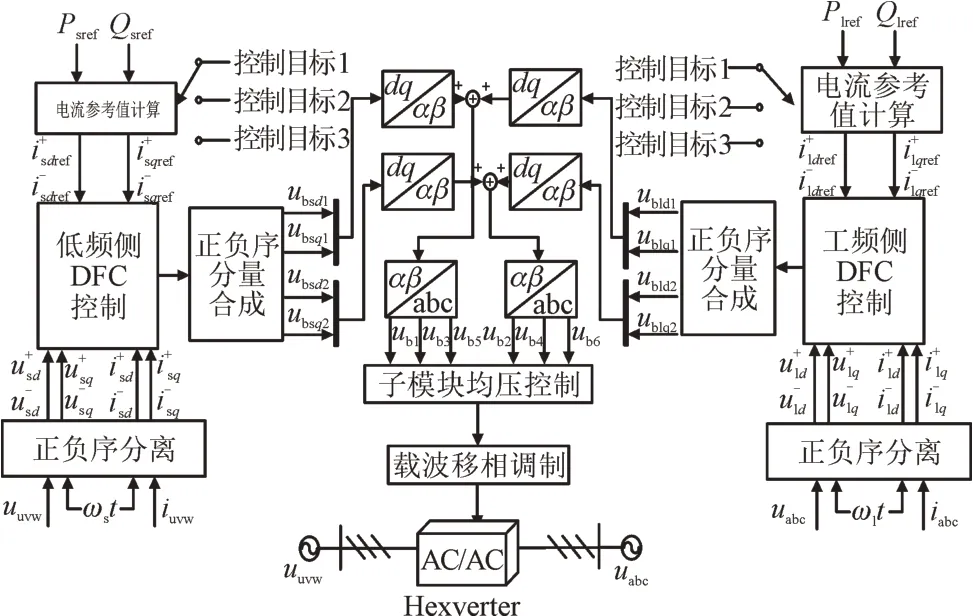
图3 电网电压不平衡下Hexverter系统总控制框图Fig.3 General control block diagram of Hexverter system under grid voltage imbalance

3 软件仿真分析

为了验证本文提出的微分平坦控制策略运用于Hexverter 系统上的可行性与先进性，在Matlab/Simulink 软件上搭建了Hexverter 控制系统的仿真（Hexverter 系统参数见表1）。并在3 种不同工况下对DFC 与PID 2 种控制效果进行对比。

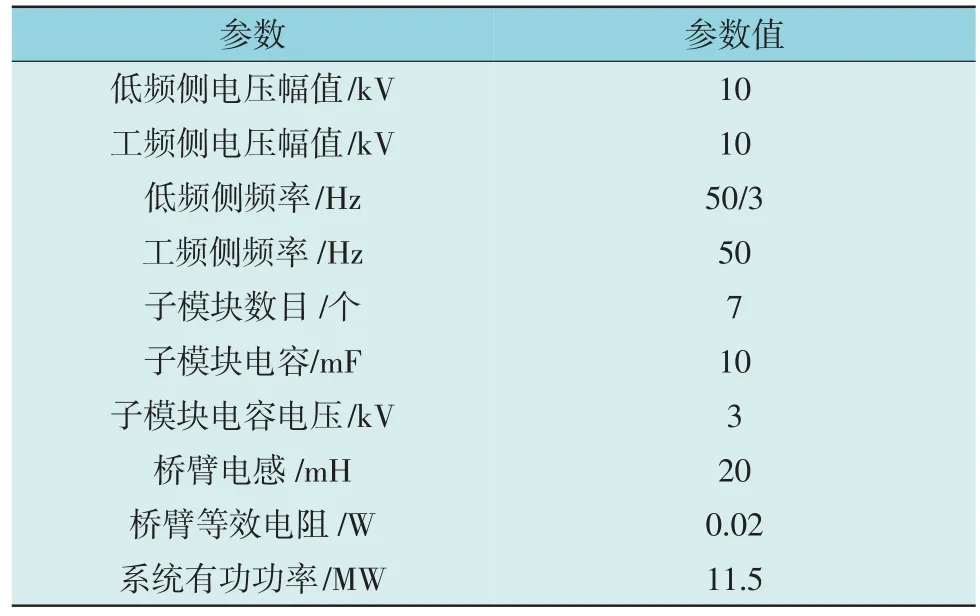
表1 Hexverter系统仿真参数Table 1 Simulation parameters of Hexverter system

3.1 Hexverter正常工况仿真分析

在正常工况下运行时，Hexverter 的DFC 控制策略的仿真波形图如图4 所示。从图4（a）—（d）可以看出，Hexverter 的低频侧与工频侧电压和电流波形均满足三相对称性；图4（e）和（g）中可以看出，低频侧于工频侧的dq轴电流分量均可以迅速稳定在由外环控制得到的期望值上；从图4（f）中可以看出，低频侧的有功功率可以快速跟踪给定Psref，使有功功率保持在11.5 MW 且无功功率为0 MW；图4（h）—（l）表明系统环流，桥臂电压、桥臂电流的波形良好，桥臂中各子模块的电容电压电压和子模块平均电容电压均很好的跟踪在给定值附近。

图4 在正常工况下Hexverter微分平坦控制的仿真波形Fig.4 Simulation waveforms of DFC strategy for Hexverter under normal operating condition

3.2 Hexverter不平衡工况仿真分析

为验证在不平衡工况下微分平坦控制策略的可行性，本文提出了2 种工况来进行验证。

1）工况1：两侧的电网不平衡控制目标由目标1（平衡电网电流）变为目标2（消除有功纹波）再变为目标1。

在0～0.1 s 时，系统正常运行，此时的低频侧与工频侧均选择控制目标1，且Ps=Pl=11.5 MW；在0.1～0.2 s 时，低频侧u 相电压跌落10%，且此时低频侧选取控制目标2，且Ps=5.75 MW，工频侧保持不变；在0.2～0.3 s 时，工频侧的b 相电压跌落12%，同时选取控制目标2，且Pl=5.75 MW；在0.3～0.4 s 时，低频侧与工频侧均恢复到控制目标1 时的状态。

2）工况2：两侧的电网不平衡控制目标由目标1（平衡电网电流）变为目标3（消除无功纹波）再变为目标1。

在0～0.1 s 时，系统正常运行，此时的低频侧与工频侧均选择控制目标1，此时Ps=Pl=11.5 MW；0.1～0.2 s 时，工频侧a 相电压跌落10%，且此时工频侧选择控制目标3，且Pl=6.5 MW，低频侧保持不变；0.2～0.3 s 时，低频侧u 相电压跌落10%，且选取控制目标3，且Ps=6.5 MW；0.3～0.4 s 时低频侧与工频侧均恢复到控制目标1 时的状态。

3.2.1 工况1仿真实验

图5 为工况1 下波形。表2 为工况1 下2 种控制策略的低、工频侧的电流分析。通过图5 和表2 数据可知，在0～0.1 s 系统正常运行时，DFC 控制下的总谐波失真（Total Harmonic Distortion，THD）更小；0.1～0.2 s 时，低频侧的u 相电压跌落10%，控制目标切换为目标2，此时PID 控制下的系统低频侧电流在0.120 5 s 达到稳定状态，谐波含量为0.58%，而DFC 控制下的系统低频侧电流在0.101 s达到稳定状态，谐波含量为0.29%；在0.2～0.3 s 时，工频侧的b 相电压跌落10%，控制目标切换为目标2，此时系统两侧均为不平衡状态，通过表2 数据可知传统PID 控制相比其稳定性与动态性能明显更好；在0.3～0.4 s 时，两侧均恢复平衡状态，在不平衡状态切换为平衡状态时DFC 控制更优。

表2 工况1下电流分析Table 2 Analysis of current under operating condition 1

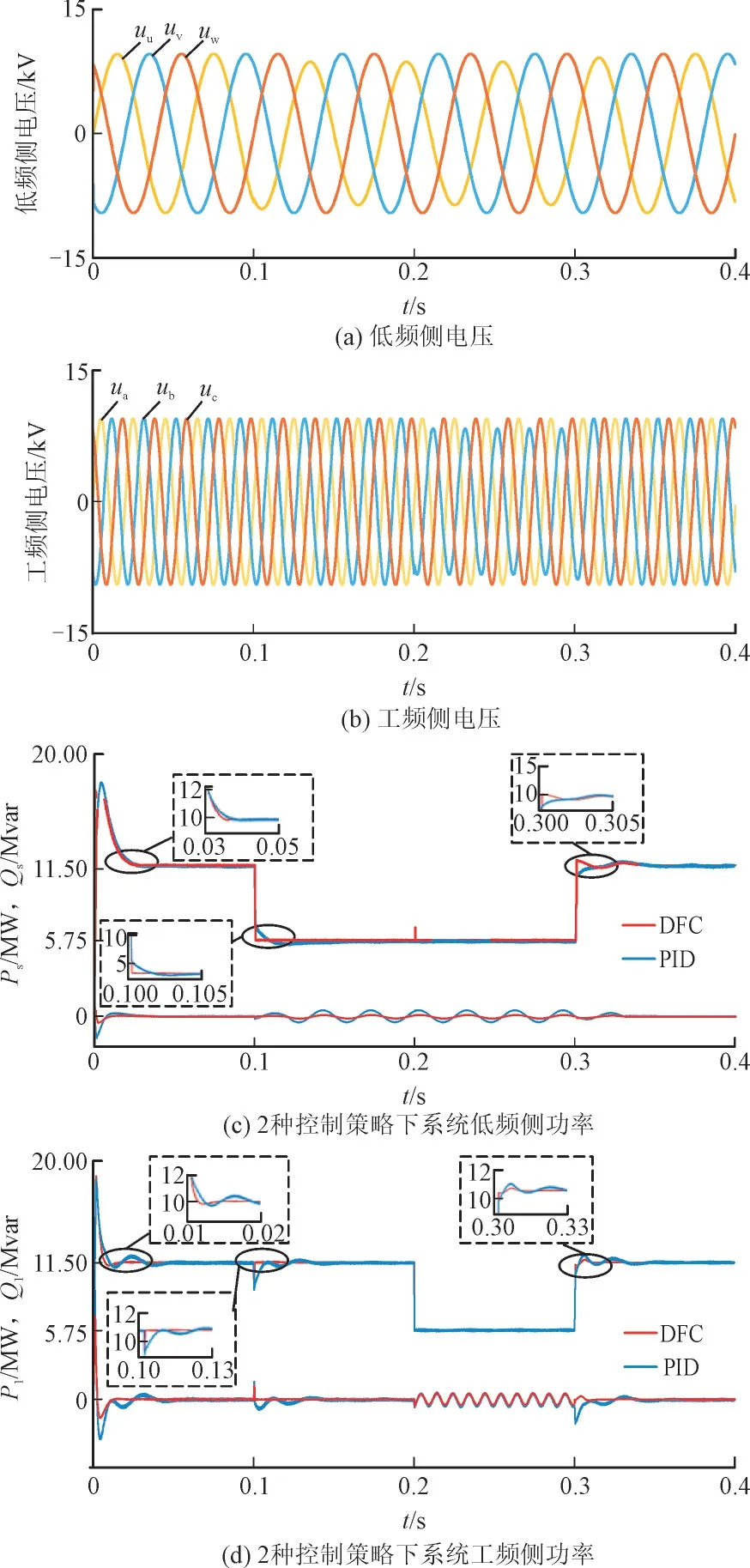
图5 工况1下波形Fig.5 Waveforms under operating condition 1

3.2.2 工况2仿真实验

图6 为工况2 下波形。表3 为工况2 下低频侧与工频侧的电流分析。通过图6 和表3 数据可知。在0～0.1 s 时，系统正常运行，两种控制策略低频侧和工频侧的电流幅值一致，且DFC 控制的稳定性与动态性能明显更好；在0.1～0.2 s 时，工频侧a相电压跌落10%，系统进入不平衡状态且选择控制目标3，由表3 可知，PID 控制下的工频侧电流在0.138 s 到达稳定状态，谐波含量为0.52%，而DFC控制下的工频侧电流在0.100 6 s 就到达稳定状态，且谐波含量仅有0.06 %；在0.2～0.3 s 时，低频侧u相电压降低10%，系统两侧均为不平衡状态，此时DFC 控制下系统低频侧与工频侧电流的稳定时间和谐波畸变率均要优于PID 控制，说明了DFC 控制在不平衡下具有较好的动态特性、快速性与稳定性；在0.3～0.4 s 时，系统两侧恢复到平衡状态，控制目标均从3 切换回控制目标1，表3 可知，在不平衡状态切换到平衡状态时DFC 控制更优。

表3 工况2下电流分析Table 3 Analysis of current under operating condition 2

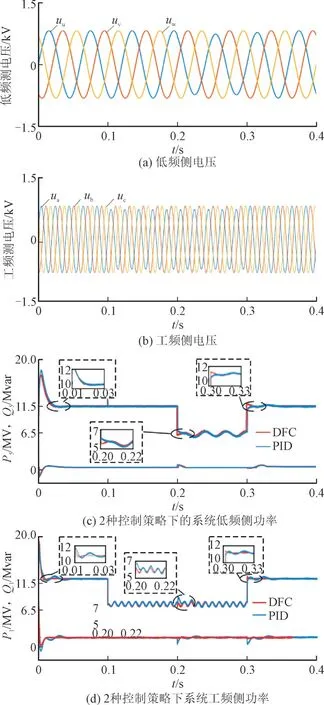
图6 工况2下波形Fig.6 Waveforms under operating condition 2

根据工况1 和工况2 实验结果分析可知，微分平坦控制策略在平衡和不平衡工况下均可正常运行，且DFC 控制的控制效果要优于PID 控制。

4 结论

本文针对Hexverter 系统运用于海上风电场中所存在的实际问题，将微分平坦控制策略运用到Hexverter 系统中，并通过理论分析和仿真实验得出以下结论：

1）本文所提微分平坦控制（DFC）策略能够满足Hexverter 的正常运行，且低频侧与工频侧的电流、电压、功率等电量都较好；系统在电网电压双端不平衡的工况下仍能正常运行，且对3 种不同控制目标的切换具有较好快速性与稳定性。

2）在电网电压不平衡工况中，无论是在低频侧和工频侧功率变化，还是低频侧和工频侧电压等级突变等工况下，本文所提DFC 控制策略的稳态性能和动态性能都要优于PID 控制策略，且两侧的电流谐波含量也要更低，控制效果也更加出色。

3）Hexverter 双端DFC 控制相比于PID 控制电流响应速度更快、动态性能更高、谐波含量更低、整体控制效果更好。