基于序优化的配电网负荷三相不平衡优化策略研究

陈申宇，陈 维，刘起蕊，冯庆燎，陈志健，邹红波

（1.广东电网有限责任公司广州供电局，广东广州 510000；2.三峡大学电气与新能源学院，湖北宜昌 443000）

0 引言

居民生产、生活的实际过程中，以单相电力负荷需求为主[1]。然而，交流输配电网传输的是三相交流潮流，为满足三相系统平衡，需要综合考虑各单相负荷所接入的相序[2]。尽管配电网规划设计时对单相负荷进行了三相平衡性分配考虑，但在实际状况下，由于电力新技术的推广应用以及家用电器的多样化发展等，用户的电能需求仍具有较大的随机性[3-5]。大功率的单相用电器一旦接入，必然给整个供电台区三相系统的平衡性造成冲击，从而导致配电网电能质量下降甚至断路器跳闸，严重影响居民“获得电力”的满意度[6-8]。因此，合理安排单相负荷接入配电网的相序可以从根本上解决配电网负荷三相不平衡问题。

现有调整单相负荷接入配电网相序的措施一般分为两类：人工换相和智能换相[9-12]。人工换相是指配网人员根据各单相电力用户的用电量数据，平衡分配相序。因人工换相费时费力，加之智能电力设备的更新迭代，智能换相已经成为相序调整的主要途径。智能换相是指利用优化算法合理计算相序后，将换相信息发送给由电力电子器件组成的智能换相装置中，实现相序的实时智能调整。因此，无论是何种调整单相负荷接入配电网相序的措施都需要以合理的相序优化算法为基础。

针对配电网负荷三相不平衡优化问题的探索，国内外专家学者进行了广泛的研究。文献[13-14]采用线性规划方法近似处理非线性三相不平衡问题，复杂度较高而精度不高。文献[15-17]使用粒子群优化算法研究了配网中单相负荷优化接入问题，文献[18-19]使用遗传算法通过模拟实际配网负荷接入来实现三相平衡，均未有效解决陷入局部最优问题。文献[20]提出了一种动态智能三相负荷平衡算法，求解效率不高，且未考虑换相开关的损耗问题，实用性不强。文献[21]提出了一种自适应混合差分进化算法，但计算效率和准确率依赖于参数手动设置，适应性不高。综上所述：从算法来看，现有研究具有两个较为突出的缺陷：一方面，这些算法未有效解决求解效率与精度间的矛盾；另一方面，较为常用的智能型算法难以解决易陷入局部最优问题，无法快速有效求取全局最优解。从三相不平衡优化问题本身来看，上述研究针对的仅仅是某一时间间隔内负荷需求不变情况下的三相负荷平衡优化，并没有考虑实际负荷的波动性。换句话说，采用上述文献算法，每次配电网中负荷动态变化时，都需要反复执行计算，这种模式占用了大量的CPU 计算资源，严重时会造成负荷换相系统宕机。

序优化算法[22-23]基于序比较思想，不寻求最优解，转而寻求足够好解，在求解包含离散型变量问题方面具有精度高、求解时间快的明显优势。目前已在工程界已经得到广泛应用，并获得较理想结果。序优化思想主要包含两步：（1）用排序比较值代替精确求值；（2）目标软化，即当精确求解目标函数的最优解在计算量上不可行或较为复杂时，松弛目标函数。本文引入序优化思想，从配网负荷三相不平衡优化问题特征入手，以分阶段逐步缩小解集范围的思路进行求解。该求解方法分为两个阶段：第一阶段，建立粗糙模型对各单相负荷接入三相系统的方式进行初筛；第二阶段，建立精确模型对初筛解集进行精确梳理，求取最优解。第一阶段以换相周期内换相开关最小动作次数为基本约束，在保证工程实际可行性的同时保留了负荷波动的区间。第二阶段利用序优化算法求解流程，基于负荷的实际测量值，求取最优的相序调整策略。

1 单相负荷接入三相系统数学模型

单相负荷连接到三相配电系统示意图如图1所示。

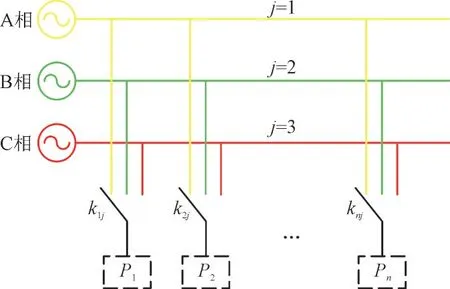
图1 单相负荷连接示意图Fig.1 Schematic diagram of single-phase load connection

图中，P1，P2，…，Pn分别为连接在配电网中的负荷值P1，负荷值P2，…，负荷值Pn；i为第i个负荷；n为负荷总数；j为相序，j=1 为负荷接于A 相，j=2 为负荷接于B 相，j=3 为负荷接于C 相；kij为负荷Pi连接在j相母线上的开关状态，kij∈{0，1}，i∈{1，2，…，n}，j∈{1，2，3}。

则配电网中全部负荷可表示为：

式中：Ptotal为连接在配电网中的总负荷值。

同时，总负荷值也可以表示为各单相负荷值之和：

式中：PA，PB，PC分别为连接在配电网母线A 相、B 相、C 相的负荷值。

各负荷连接到特定相序是通过特定换相开关实现的。如图1 所示，各相母线上的负荷表示为：

kij=0 为负荷i与j相母线未连接；kij=1 为负荷i与j相母线连接。由于换相开关同时刻只有一个切换状态，kij还应满足以下约束：

式（1）—式（4）仅表示单一时刻下各单相负荷间的关系。然而，要研究较长时间段内负荷三相不平衡问题的治理需要考虑不同的时间间隔。

每个时刻t，A 相负荷与换相开关间的关系表示为：

式中：PTA为每时刻T连接在A 相上的负荷；kTn1为每时刻T第n个负荷需求连接在A相上的负荷。

对式（5）求和后整理后可得三相负荷与换相开关间关系：

1.1 目标函数

配电网负荷三相不平衡治理的首要目标是维持负荷三相不平衡度最小。同时，配电网中，换相开关一般是由电力电子器件组成，其寿命与转换次数密切相关。转换次数越高，开关寿命越短，因此，换相开关的动作次数也应该作为目标函数考虑。

以三相不平衡度[24-25]构成的目标函数F1表示为：

以换相开关动作次数构成的目标函数F2表示为：

总目标函数F为目标函数F1与目标函数F2的加权：

式中：λ1为目标函数F1所占的权重，代表三相不平衡所带来的成本损失[24]；λ2为目标函数F2所占的权重，代表转换次数所带来的成本损失[24]。

1.2 约束条件

约束条件包含：换相开关动作逻辑约束、换相开关动作次数约束、功率平衡约束、负荷与换相开关间耦合约束、三相不平衡度约束。

1）同一时刻每个负荷的换相开关只有一个切换状态，如式（4）所示。

2）每时刻T每个换相开关动作次数的受上限约束：

式中：Nki为换相开关z在每时刻T转换次数的上限。3）任意时刻每相负荷之和等于该时刻总负荷：

4）三相负荷与换相开关间的耦合约束如式（6）所示。

5）受线损等因素影响，配电网负荷三相不平衡度应小于某一数值：

式中：UBA，UBB，UBC分别A 相、B 相、C 相负荷不平衡度的上限。

2 基于序优化算法的模型求解

序优化算法[26-27]是一种适用于离散型变量模型求解的高效算法。本文引入序优化算法，在序比较的过程中保证求解精度并实现求解效率的提升。首先以换相开关为变量构造粗糙模型对初始解空间进行预筛选，大幅度减少变量解空间的规模，得到选定集合；然后再构造考虑负荷平衡等约束的精确模型对选定集合中的解进行排序，最终求得最优解。如图2 所示。图中OPC 为排序性能曲线（Order Performance Curve，OPC）。

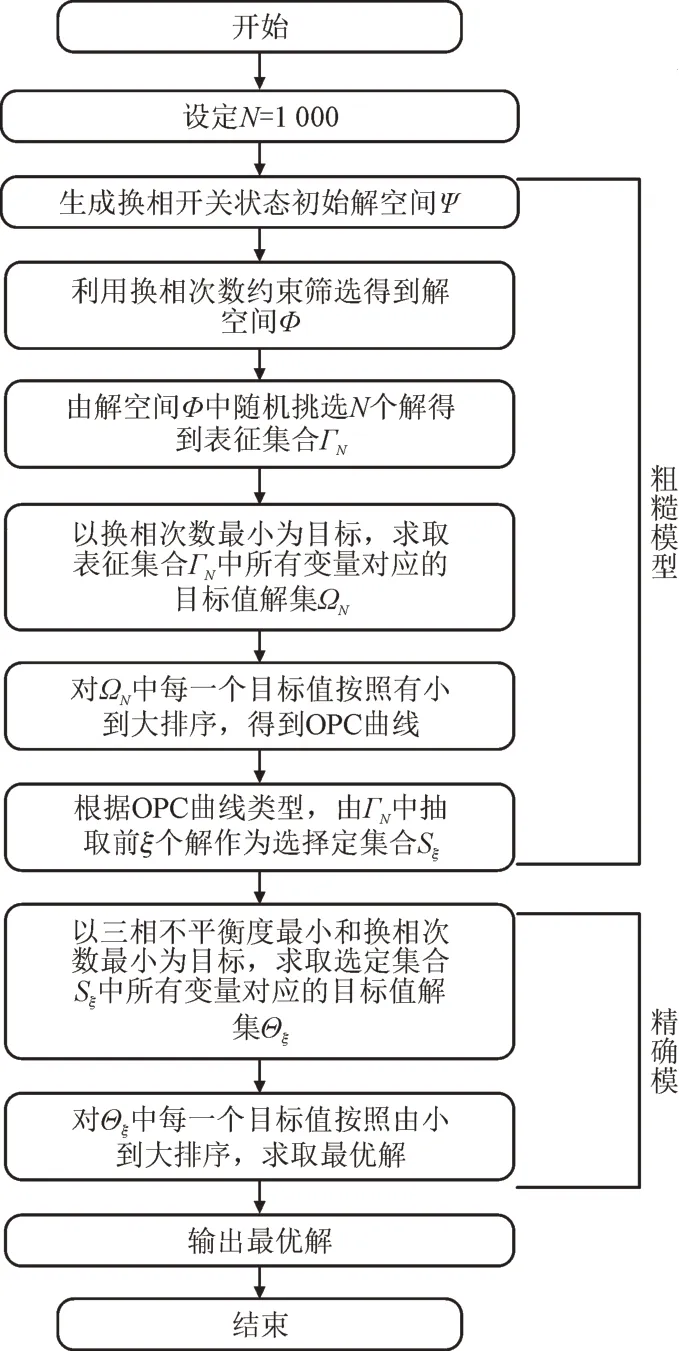
图2 序优化算法的求解流程Fig.2 Solving process of OO algorithm

2.1 序优化算法求解步骤

序优化模型的建立及求解包含2 方面；（1）粗糙模型：以换相开关为变量，考虑换相开关状态约束，以换相次数最小为目标，初筛目标解集；（2）精确模型：以初筛目标解集中的换相开关为变量，考虑三相负荷约束，以三相不平衡度最小和换相次数最小为目标，求解最终结果。

2.2 粗糙模型求解步骤

以换相开关动作逻辑、换相开关动作次数为基础，对换相开关状态集合进行粗筛。

1）生成换相开关状态初始解空间Ψ。

2）利用换相次数约束式（4）筛选得到解空间Φ。

3）由解空间Φ中随机挑选N（N=1 000）个解得到表征集合ΓN。

4）以换相次数最小为目标，求取表征集合ΓN中所有变量对应的目标值解集ΩN；目标函数为式（8）；约束条件为式（4）和式（10）。

5）对ΩN中每一个目标值按照有小到大排序。

常见的OPC 曲线有Neutral 型、Steep 型、Flat型、Bell 型、U-Shaped 型5 种，如图3 所示。

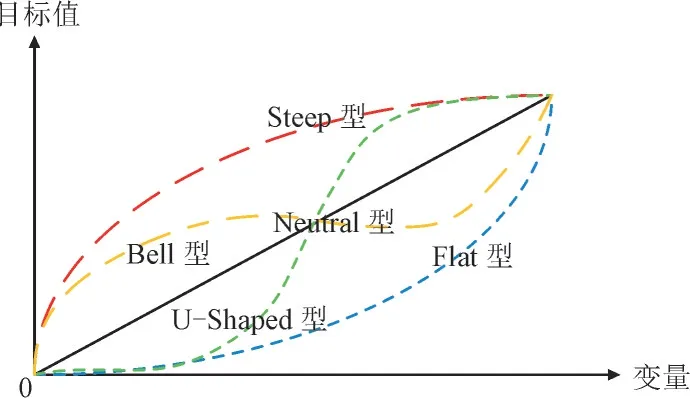
图3 OPC曲线的几种类型Fig.3 Several types of OPC curves

6）对比图3 确定本文方法的OPC 曲线类型。根据OPC 曲线类型确定式（15）中的参数值，并最终求得ξ的值。在经过排序处理后的ΓN集合中选取前ξ个解构成选定集合Sξ，Sξ的求解公式为：

式中：e为常数，e≈2.718；ξ为选定集合Sξ中解的数量；f为足够好解的数量；g，ξ0，ρ，γ为回归参数；η为随机噪声分量，其值查文献[25]。

2.3 精确模型求解步骤

1）以三相不平衡度最小和换相次数最小为目标，求取选定集合Sξ中所有变量对应的目标值解集Θξ；目标函数为式（9）；约束条件为式（6），式（11）—式（14）。

2）对目标值解集Θξ中的每一个目标值按照由小到大排序，选取目标值最小的解对应的变量值作为模型的最优解。

3 算例分析

本章分别在2 个配电系统上验证所提方法的有效性。首先验证所提方法在模拟配电网系统中的有效性，然后节选实际配电网验证所提方法有效性。最后，将所提方法与现有典型的配电网负荷三相不平衡优化方法应用情况进行对比。

设定相序调整周期Γ=72 h，每24 h 调整计算1次换相开关状态。计算在英特尔酷睿i5-7500 处理器，16 GB 内存计算机上完成，算法基于Matlab 2019a 平台编程实现。

3.1 基于模拟配电网的求解结果

本节以20 个单相负荷节点组成的模拟配电网为基础验证算法的有效性。表1 为20 个单相负荷换相开关的初始状态，0 表示负荷未接入该相，1 表示负荷接入该相。图4 为20 个单相负荷连接到配电网A，B，C 三相的总负荷需求曲线。

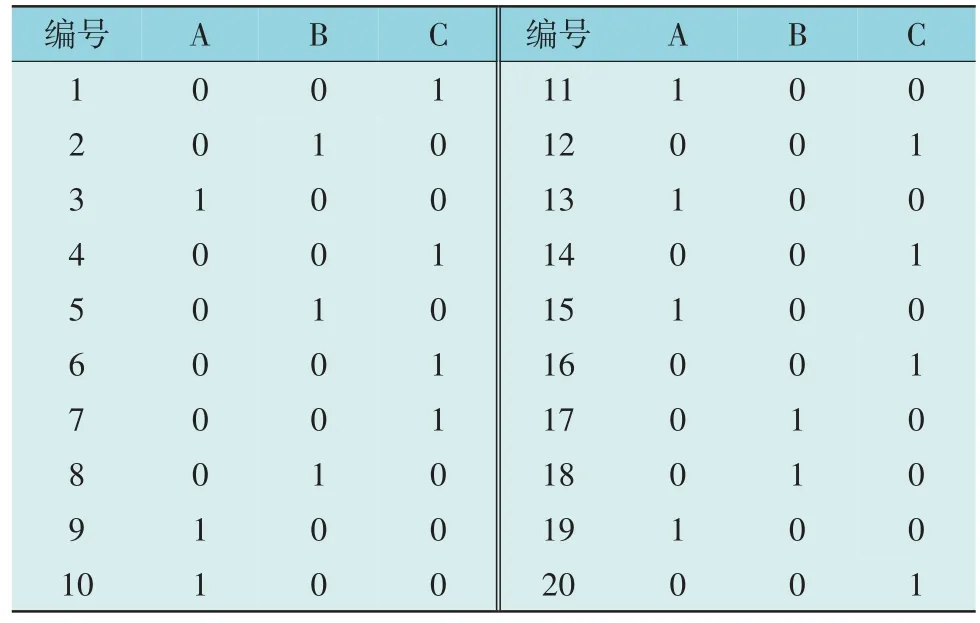
表1 20个单相负荷换相开关的初始状态Table 1 Initial state of 20 single-phase load transfer switches

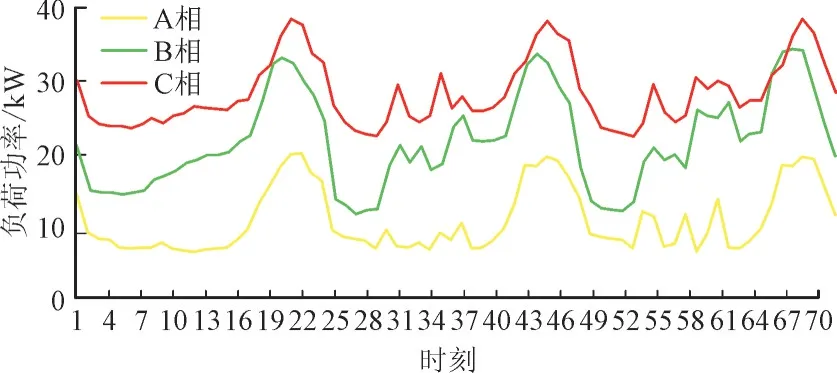
图4 优化前配电网A，B，C三相总负荷需求曲线Fig.4 Demand curves for three-phase total load of distribution network before optimization

按照式（7）计算图4 的三相不平衡度为0.21。

3.1.1 算法求解过程分析

按照2.2 节序优化粗糙模型求解得到的OPC曲线如图5 所示。

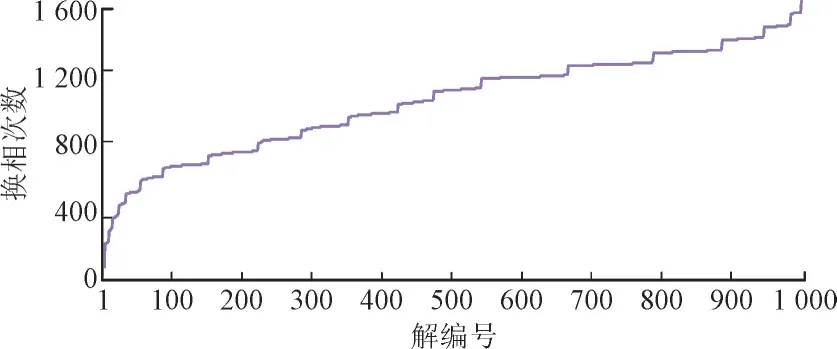
图5 序优化粗糙模型获得的OPC曲线Fig.5 OPC curve obtained by OO rough model

由图5 可以看出，计算求得的OPC 曲线呈阶梯状，其原因是，不同方案对应的换相次数可能相同，而同一换相次数可能对应多个负荷分配结果。对比标准OPC 曲线，确定本文方法的OPC 曲线类型为Bell 型。根据文献，确定Bell 型OPC 曲线下式（15）中的各项参数分别为：ξ0=8.199 8，ρ=1.916 4，γ=-2.025 0，η=10，g=20，f=1。将参数代入式（15），求得ξ=19，即选定集合Sξ中解的个数为19。将粗糙模型筛选得到的选定集合Sξ中解代入2.3 节精确模型求解，求解结果如图6 所示。

图6 精确模型的求解结果Fig.6 Solution results of accurate model

从Sξ集合中选择目标函数（F值）最小方案对应的换相开关状态作为三相不平衡优化模型的决策结果。求解的换相开关状态如表2 所示。表中编号表示单相负荷所连接的相序，例如“001”表示该负荷连接在C 相。按照所提方法优化后的三相负荷曲线波动情况如图7 所示。

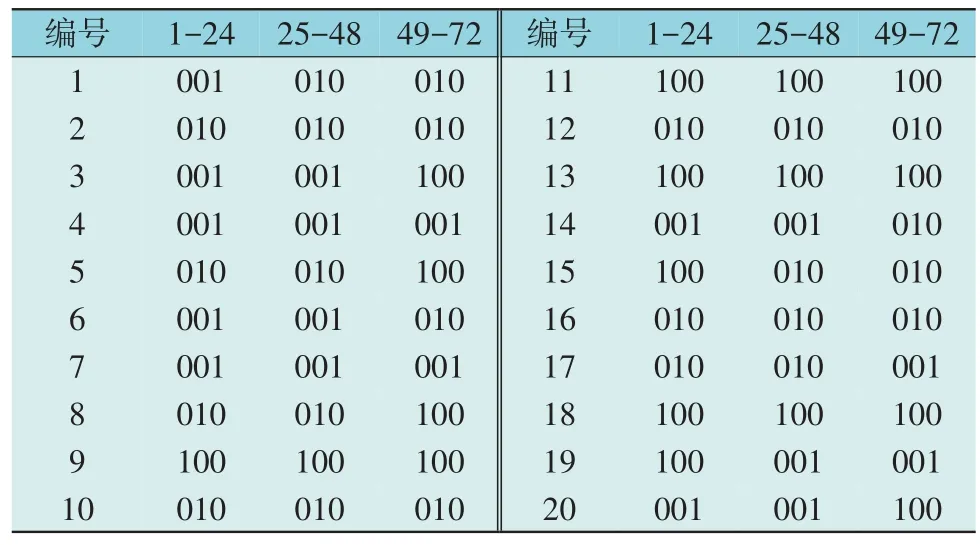
表2 20个单相负荷换相开关状态Table 2 State of 20 single-phase load transfer switches

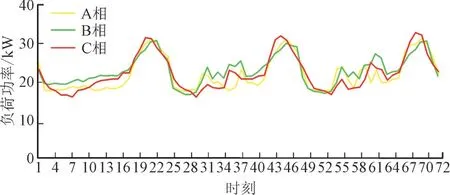
图7 优化后的配电网A，B，C三相总负荷需求曲线Fig.7 Demand curves of three-phase total load of distribution network after optimization

优化后的负荷三相不平衡度为0.03，相比于初始系统，三相不平衡度降低了18%。

对比图4 和图7 可知，采用三相不平衡优化方法优化后三相负荷基本达到平衡。对比表1 和表2可知，换相开关次数最多为2 次，表明所提方法有效考虑到了换相开关频繁动作带来的成本增加问题。综上所述，所提方法有效解决了单相负荷三相不平衡问题。

3.1.2 算法稳定性分析

为进一步验证序优化算法的稳定性，本节随机生成20 组单相负荷换相开关的初始状态和对应的配电网A，B，C 三相总负荷需求曲线，然后计算分析20 个算例的三相不平衡度（式（7））。其结果如表3 所示。

表3 20个算例的三相不平衡度Table 3 Three-phase unbalance degree of 20 examples

由表3 可以看出，所提方法在不同负荷分配模式下求解的三相不平衡度稳定在0.03 左右，表明该方法具有较好的稳定性。

3.2 基于实际配电网的求解结果

为了进一步验证所提方法在实际配电网的有效性和优越性，本节将对比所提方法与文献[13]、文献[15]、文献[18]、文献[20]4 种方法的计算效率与精度情况。为突出算法对比的有效性，各文献方法均以本文建立的多目标模型为基础进行求解。

为验证所提方法在面对负荷小范围波动情况下求解效率的稳定性，设定10 个可变负荷算例，其负荷范围值为标准负荷的98%～102%。标准负荷值取自河南省某市实际配电网数据，图8 为河南省某市实际配电网低压380 V 三相系统网架图，其中系统中单相负荷有48 个。以式（9）为目标，各方法求解结果如表4 和表5 所示。

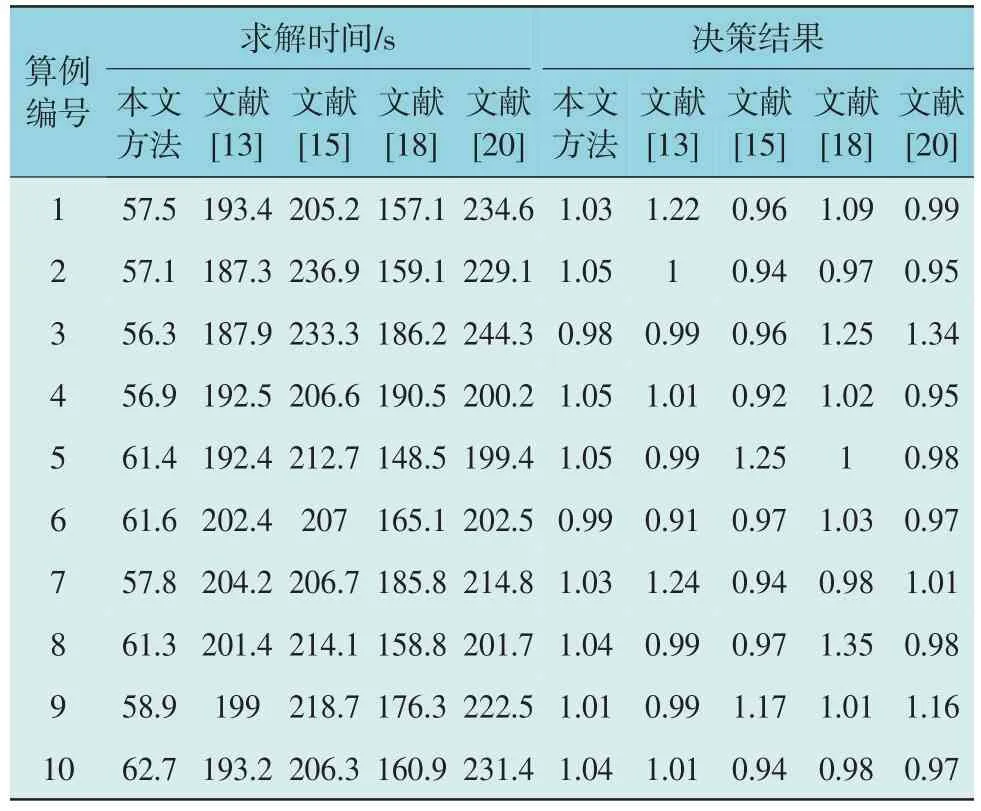
表4 各方法求解结果对比Table 4 Comparison of solution results among various methods

表5 各方法求解结果的统计指标对比Table 5 Comparison of statistical indicators for solution results among various methods

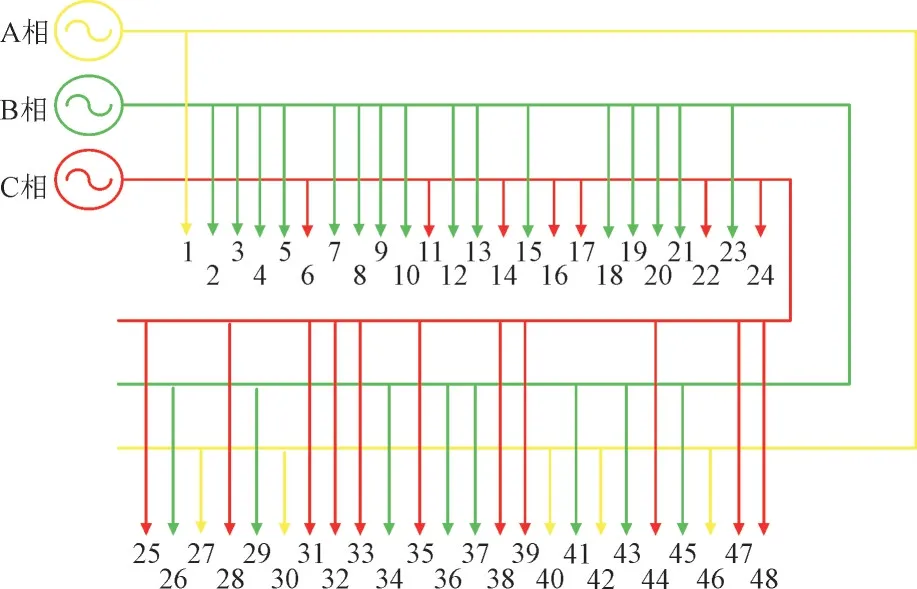
图8 实际配电网三相系统图Fig.8 Three-phase system diagram of actual distribution network

由表4 和表5 可以看出，就平均求解精度而言，本文的序优化算法的决策结果会存在略高于其他文献方法的情况，其原因是，序优化理论的基本思想就是通过放弃寻求最优解，转而致力于寻求足够好解来实现其大幅度提升算法求解效率的目的。同时，通过对比各文献方法求解结果的方差指标可以看出：本文方法的方差值最小，表明本文方法求解精度的稳定性较好。

就平均求解效率而言，与其他算法相比，本文方法求解效率得到了显著提升，其求解效率比文献[20]算法提升了约5 倍，比文献[18]的方法提升了约3 倍。本文提出的改进约束序优化算法计算效率得到提升的主要原因是：（1）通过序优化粗糙模型、精确模型筛选解空间，有效降低了解空间的维度，从而大幅提升了序优化算法的计算效率；（2）序优化粗糙模型仅初筛了换相开关的状态解集，该解集能够有效包含小范围负荷波动，在面对配电网中负荷动态变化情况时，无需反复执行计算，缩短了求解时间。另外，通过对比各方案求解时间的方差指标可以看出：本文方法的方差值最小，表明本文方法求解时间的稳定性较好。

综上所述，对比结果表明本文方法的求解稳定性较高，在不失求解精度的前提下提升求解效率约3-5 倍以上。

4 结论

本文提出了一种基于序优化的配网负荷三相不平衡优化策略，适用于具有高聚集特征的配电台区。通过仿真算例结果得到以下结论：

1）所提方法能够有效避免配电网负荷三相不平衡问题求解易陷入局部最优的情况。与其他方法相比，在提高了计算效率的同时保证了较高的求解精度。

2）基于序优化的求解方法能够有效适应负荷小范围波动情况，无需每次反复执行计算，提高了求解效率。

3）所提方法在面对不同配电网网架和不同负荷需求情况下仍然能够保持较强的稳定性。