区域一致趋同的分布式负荷频率控制方法研究

周一辰，杨 洋，李永刚，楚玉建，李金泽，林 卉

（新能源电力系统全国重点实验室（华北电力大学），河北保定 071003）

0 引言

新型电力系统大力发展以风光为代表的可再生能源发电方式[1]，传统火电机组的占比不断下降，频率调整能力逐渐弱化。电力系统逐渐表现出源荷双端不确定性[2-4]，系统干扰发生的频次与幅度均有所增加[5-6]，有功功率不匹配引起的频率波动幅度增大，亟需发展更加高效地频率调整方式。

负荷频率控制（Load Frequency Control，LFC）负责将电力系统频率以及联络线交换功率维持在预定值。按频率控制信号求取方式的不同可将LFC 的研究分为3 种类型，分别为集中式LFC、分散式LFC和分布式LFC（Distributed Load Frequency Control，DLFC）。集中式LFC 由中央控制器负责求取调节信号[7]，通过最优控制[8]或智能算法等方式确定控制器参数。集中式LFC 需要借助大量系统信息，对控制器计算性能和通信可靠性要求很高[9]。分散式LFC 各区域控制器独立运行，缓解了集中式控制的计算与通信压力；但系统互联程度高时，由于控制器相互独立而未考虑区域间的关联，其调节缺乏全局性[10]。DLFC 在分散式LFC 基础上结合区间通信，借助本地信号与区域信息得到调节信号，既减小了计算量又考虑了控制的全局性，是当前主要研究方向[11-12]。

电力系统广域量测技术与通信技术的发展，促使分布式控制广泛应用[13-14]，并使区域间互联互通以提高系统调节性能。文献[15]对分布式模型预测控制在电力系统中的应用做了综述与展望。文献[16]提出了一种基于分布式模型预测控制的DLFC 系统，然而调节信号的物理意义并不清晰。随着电力系统逐渐呈现高比例可再生能源与高比例电力电子设备“双高”特征，系统的频率时空分布差异化愈发明显[17]，在电力系统出现扰动后不同区域的频率动态将存在显著差异，这需要提高区域间的互济水平，以避免对互联系统的稳定运行产生不利影响。近年来，在多智能体一致性问题的研究中，一致性算法具有使各智能体状态趋同的特性。文献[18]采用无领导一致性算法设计各区域LFC 控制器提高了多区域频率调节的关联性，然而所有状态的一致并不符合调频特性，同时区间信号传输过程存在的时滞问题也需要考虑。

本文提出一种结合多智能体一致性算法与动态面控制的电力系统DLFC 方法，并将区域频率间的偏差量作为频率调节的一部分，以频率调节过程中区域间频率的一致性作为调节需求，降低区间调频过程的差异性，同时保障在时滞环境下的频率调节性能。首先，构建分布式LFC 系统的模型框架，并设计一种具有双重观测功能的分散式观测器。其次，考虑通信时滞以修正多智能体一致性算法（Multi-agent Consensus Algorithm，MAC）并基于动态面控制法（Dynamic Surface Control，DSC）设计控制器结构。最后，基于2 区域与4 区域互联系统算例验证方法的控制效果与性能。

主要贡献包括：（1）建立新型DLFC 系统，提高频率调整性能；（2）设计具有状态与干扰双重观测功能的分散式系统观测器，获取未知系统信息；（3）结合时滞修正的多智能体一致算法与动态面控制法设计控制器，适应通信时滞环境。

1 DLFC系统设计

DLFC 系统设计中，首先引入互联电力系统的区域聚合频率控制模型，然后介绍系统框架以及分布式控制间的通信设置。

电力系统根据电网各节点频率变化的相似程度以及地理接线结构可以划分出多个经联络线互联的区域子系统并设置对应频率控制中心，各子系统连接关系如图1（a）所示，频率控制中心间经通信实现信号传递。

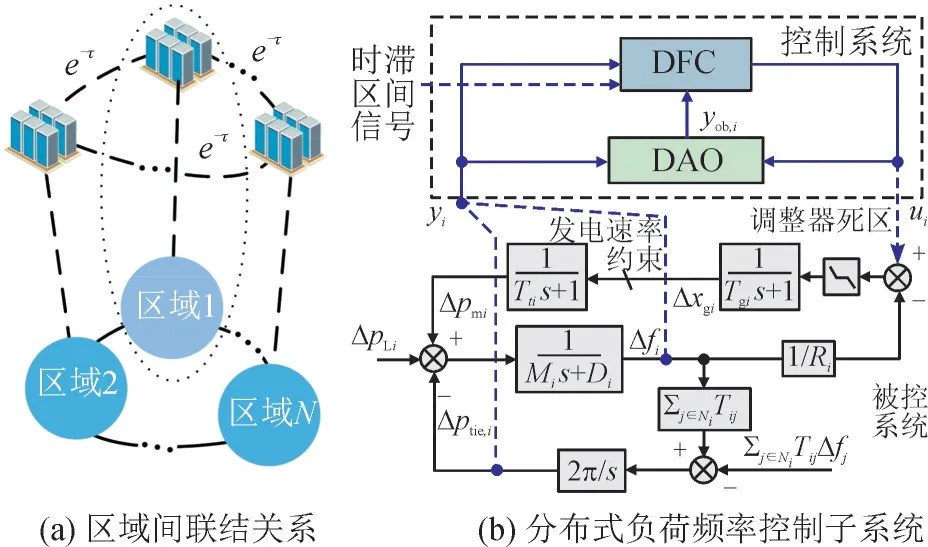
图1 分布式负荷频率控制系统模型Fig.1 Distributed load frequency control system model

考虑到各区域内通常具有多台机组，其频率控制模型不仅维数过高，而且也不利于控制器设计，为简化模型，基于聚合频率响应模型将多机结构聚合[19]，并采用等效发电机作为惯量中心（Center of Inertia，COI）代表整个区域所有发电机组[20]。将联络线动态的耦合部分视为扰动信号，以非再热式火电机组为例，第i个区域的聚合被控系统模型如式（1）所示：

式中：i为第i个区域；xi(t)为区域i中聚合模型的状态向量；ui(t)为控制信号；di(t)为区域i中干扰向量；yi(t)为输出向量；Δfi为频率偏移量；Δptie,i为联络线功率偏差量；Δpmi与Δxgi分别为等效原动机机械功率与调速器输出位置变化量，通过设计观测器获取；ΔpLi为负荷增量；Tij为区域i与区域j间联络线同步系数；N为互联区域个数；Ai，Bi，Ei，Ci分别为区域聚合模型状态、控制、干扰与输出矩阵；Tti为等效原动机惯性时间常数；Tgi为等效调速器惯性时间常数；Ri为一次调差系数；Mi为机组惯性常数；Di为阻尼系数；ACEi为区域i中控制偏差信号；βi为响应系数。

DLFC 系统如图1（b）所示，核心包括分散式区域观测器（Decentralized Area Observer，DAO），负责提供聚合模型定义的观测信号；还包括分布式频率控制器（Distributed Frequency Controller，DFC），负责计算频率调节信号。受多智能体一致性研究的启发，将频率偏差量视为区域间的一致变量，将其纳入频率控制中可以降低调频过程中各区域间的频率差异。所需要的测量信号，如Δfi与Δptie,i，经同步相量单元实时采集处理，再通过广域测量系统区内通信传送到各区域控制中心。同时区域频率偏移量以及观测信号将由各控制中心的电力调度数据网实现区间通信交换。

在所设计的框架中，区间与区内两种通信均基于TCP/IP 协议保证信号传输的可靠性。而对于因通信而产生的延迟现象，将信号传输耗时与操作耗时统一考虑为通信时滞。考虑各控制中心间基于高速通信骨干网进行实时通信，其通信时延在50 ms左右，然而通信中大于1 s 的操作时延将显著增大区间通信时滞[21]。对于区内通信则主要考虑远程终端单元、控制器与调节设备间测量与控制信号的传输[22]，文献[23]实测区内通信时滞约100 ms，因此在控制器设计中不考虑该时滞。

在区间信号传输过程中，对于第i个区域的信号xi(t)，经过通信时滞τ其它区域接收到信号为xi(t-τ)，基于2M 专用通道进行通信传输将保证每一个信号的时滞具有上界，即τ∈(0,τmax]。

2 DAO设计

基于输入解耦的思想[24]，设计出一种具有状态与干扰双重观测功能的DAO，其结构如式（2）所示：

式中：zi∈ℜ4×1，qi∈ℜ4×1分别为区域i中状态与干扰观测部分的辅助向量；Fi，Hi，Ti，Ki为状态观测部分的设计参数矩阵；为干扰观测的设计参数矩阵；yi为输出向量；yob,i为观测器的输出向量；Cob,i为观测器的输出矩阵；Dob,i为观测器的直接传递矩阵；为等效原动机机械功率变化量的观测值；为等效原动机调速器输出位置变化量的观测值；为负荷增量的观测值；为设计观测器定义的辅助系数矩阵；Ii为4阶单位矩阵；04×4为4阶零阵；I1×4为1行4列矩阵；01×3为1行3列矩阵。

由观测器中定义的辅助向量可以得到被控系统的状态向量以及干扰向量的观测向量，观测向量与辅助向量间的关系为：

3 DFC设计

作为DLFC 的核心，各区域DFC 负责计算区域控制信号。为便于控制器设计，首先对被控系统作线性变换得到严格反馈型系统结构，然后基于此描述形式，结合MAC 与DSC 设计出误差面以及控制律，完成DFC 设计。

3.1 被控系统形式改写

考虑到原系统中联络线功率偏差量Δptie,i可测量，故将式（1）降阶后进行线性变换，得到具有严格反馈形式的系统描述式（4）。

式中：xi,1，xi,2，xi,3分别为改写系统描述的状态变量；uLTi为待设计控制信号；为输出信号；fi,1与fi,3为已知状态量函数项；gi,2与gi,3为未知状态量的函数项；di,1为干扰项。

严格反馈型系统描述下，各状态变量只受下级状态变量以及外界输入量影响。其结构如图2 所示。

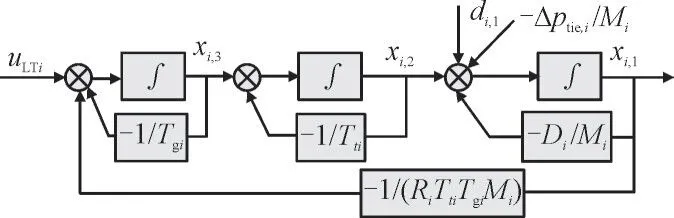
图2 严格反馈型系统结构Fig.2 Strict feedback system structure

3.2 基于DSC法的控制律设计

系统调频的关键在于维持供需端功率匹配，控制律计算各发电设备出力的调节信号。基于DSC法首先应构造误差面，而后根据误差面设计实际控制律。

误差面描述了系统状态与期望动态间的误差关系，基于MAC 算法将各区域频率偏移信号视为一致变量作为协同误差量的一部分，在系统调节过程中促使各区频率变化趋于一致。同时，将本区域的ACE信号作为协同误差量的另一部分以提高频率控制性能。以区域i为例，定义各区域误差面：

式中：ei,m(m=1,…,3) 为定义的系统误差面；ei,1为协同误差量；ei,2和ei,3分别为状态变量xi,2和xi,3与基于DSC 法设计的虚拟控制律αi,1和αi,2间的误差量；y′j为区域j的输出信号；Ni为区域i的邻接点集；aij为区域i与区域j的邻接权重，相互通信的区域权重不为零；bi,1为ACEi信号权重。

考虑到通信时滞现象，并结合DSC 法设计要求与观测器的影响，对误差面做以下修正与分析：

1）针对区间通信存在的通信时滞，定义区域i与区域j间通信时滞为τij，经过通信时滞τij的区域j输出信号为y′j(t-τij)，为使控制器具备时滞适应性，修正协同误差量ei,1。根据代数图论定义节点入度，并考虑ACE信号的定义式整理得：

2）虚拟控制律表征系统期望动态，但式（5）定义的误差ei,2和ei,3会导致控制律设计引入高阶微分，产生“微分爆炸”问题。将αi,1和αi,2分别用其低通滤波值λi,1和λi,2代替则转化为代数运算以解决，修正误差量ei,2和ei,3为：

一阶低通滤波环节表达式如下：

式中：τi,l为滤波时间参数；λi,l(0)=αi,l(0)；l=1，2。

滤波器输出误差为ηi,l=λi,l-αi,l，表征低通滤波值与虚拟控制律间的误差。记ψi,l=，滤波输出误差的动态可表示为η˙i,l=-ηi,l/τi,l-ψi,l。

3）在控制设计中使用DAO 输出的观测值将引入观测误差：

联立式（7）、式（9）和式（10）得到关系式：

设计控制律保证所定义的误差面稳定收敛，则系统状态按照所设计的各虚拟控制律运动，提高频率控制性能并保证互联系统频率变化的整体性。逐级构造关于误差面的能量函数并考虑干扰补偿，以区域i为例，基于文献[25]的方法，设计出各虚拟控制律以及实际控制律如式（12）。

定义误差面式（6）和式（7），设计控制律式（12），完成DFC 设计。图3 为DFC 的结构框图，在展示上存在一定简化，如par代指对应信号经整理后的系数，邻接信息项代指经区间通信接收的相邻区域信号，F()· 代表有关变量的函数。

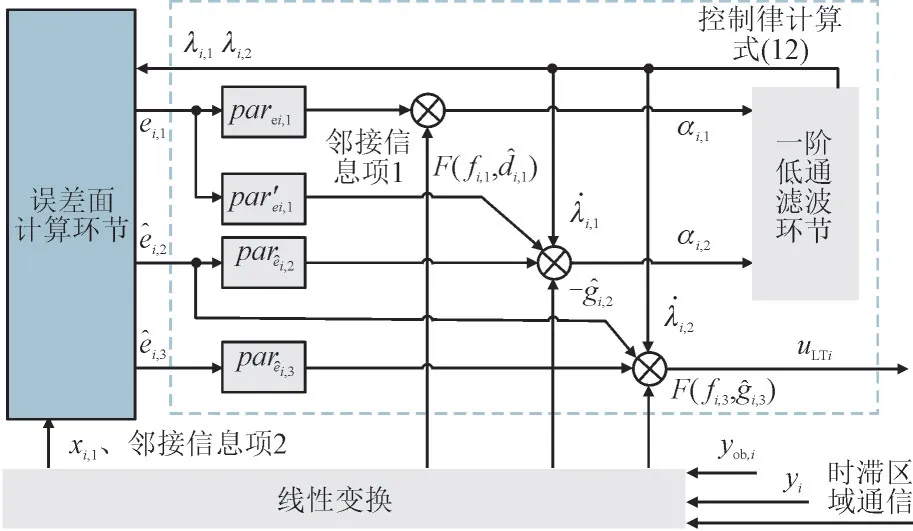
图3 控制器结构框图Fig.3 Structure diagram of controller

4 算例分析

对所设计DLFC 系统的频率调整效果进行检验。电力通信时延一般为百毫秒，固定操作时延2 s，设置区域间最大通信时滞为2.5 s，区域内最大通信时滞为200 ms。

4.1 2区互联系统的LFC控制效果分析

通过2 区互联系统验证DFC 设计的有效性与优越性。考虑2 个区域各有6 台火电机组，机组参数相同，原动机部分非线性环节中发电速率约束与调速器死区分别取为0.001 7 p.u./s 与0.033 Hz[26]，基于文献[19]计算等效模型参数，各类参数设置详见表1与表2，Km为各火电机组输出比例系数。区域1 与区域2 间联络线系数T12=T21，均设置为0.2 p.u.，频率控制器的设计参数取为：c1=0.1，c2=0.2，c3=1。

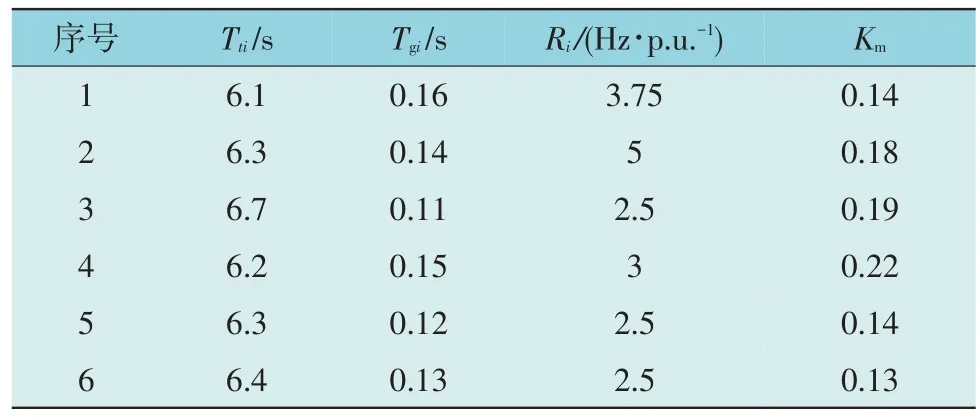
表1 6台火电机组参数Table 1 Parameter settings of six thermal power units

表2 聚合系统参数Table 2 Parameter settings of aggregated system

在t=1 s 时刻为区域1 施加0.06 p.u.的阶跃干扰量，考虑系统二次调频，分别对比传统比例积分控制器（PI）、DFC 以及文献[27]提出的分布式控制器的LFC 效果。在3 种调频措施作用下，区域1 的频率变化过程如图4 所示。

DFC 与文献[27]所设计的频率控制器均利用了干扰信息[28]，提高了干扰发生初期的反应速度；因此，频率最大偏移量Δfnadir分别为0.15 Hz 与0.16 Hz，恢复至稳定的调节时间ts分别为7.5 s 与12.4 s。传统PI 控制下系统频率最大偏移量为0.21 Hz，系统动态则需要26.8 s 的调节时间恢复稳定。从图4中可看出DFC 作用下系统动态变化平缓，有利于频率稳定。

表3 为3 种控制措施下的频率控制性能指标，相比于传统PI 控制，采用DFC 后时间乘以误差绝对值积分指标（Intergral Time Absolute Error，ITAE）提升73.1%，频率最大偏移量减小0.06 Hz。相较于传统PI 控制器，DFC 明显改善了系统干扰后频率最大偏移量与恢复速度，提高了系统频率响应性能。

表3 频率控制性能指标Table 3 Performance indicators for frequency control

4.2 4区互联系统的LFC控制效果分析

在具有明显互联特征的4 区互联系统下验证DFC 对于系统整体调频特性的改善，图5 展示了互联系统区域间通信拓扑，虚线代表区间通信。各类参数设置如表4 所示。

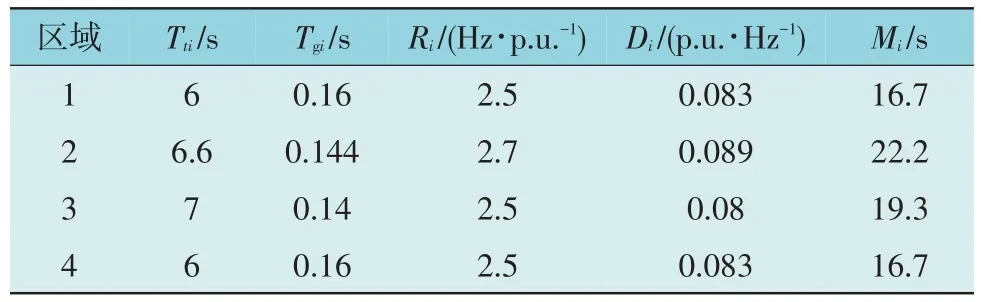
表4 4区域系统参数Table 4 Parameter settings of four-area interconnected system

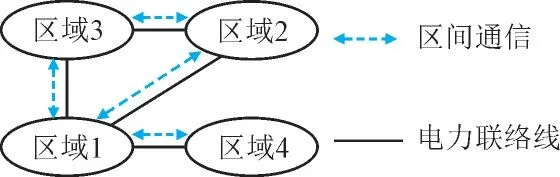
图5 互联系统通信拓扑Fig.5 Topology of communication among areas in interconnected system

区域i与区域j间联络线系数Tij均为0.2 p.u./Hz，DFC 的设计参数取为：c1=0.5，c2=2，c3=5。

在t=1 s 与46 s 时刻依次为区域1、区域4 施加0.06 p.u.的阶跃负荷干扰，在DFC 以及传统PI 控制器各自作用下，各区域动态过程如图6 所示。

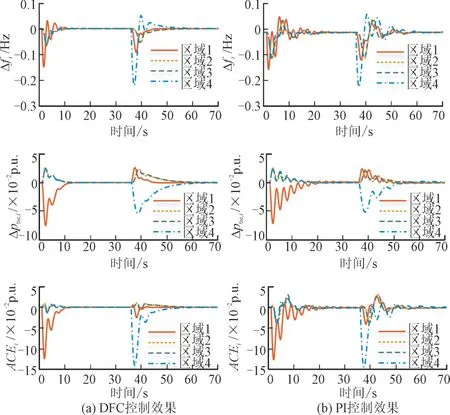
图6 4区域互联系统动态过程Fig.6 Dynamic of four-area interconnected system

从图6 可以看出，在传统PI 控制作用下系统频率调节过程中各区域的频率间差异性较大，基于本文所设计的EF指标，传统PI 控制器EF指标为3.34，DFC 的EF指标为2.17，相比之下区域间频率的差异性降低了35%。同时根据仿真结果可以看出，在DFC 作用下，各区域频率动态不仅更加平稳，且在恢复过程中具有相似的变化趋势，降低了区域间频率的差异性。在系统频率调节过程中，经联络线实现区域间有功功率的互济，直观展现了DFC 保障了区域协同的特性。同时随着系统频率变化趋势的一致，联络线功率偏差量也不再振荡，并最终恢复稳定。

5 结论

为提高广域互联电力系统频率调节性能，建立了分布式负荷频率控制系统。基于输入解耦的思想设计分散式区域观测器提供系统未知信息观测值，基于多智能体一致性算法与动态面控制法设计出分布式频率控制器。主要结论包括：

1）基于时滞修正MAC 所设计的控制器具有了时滞适应性，保证了时滞环境下的控制效果。

2）与传统控制措施相比，频率控制性能指标提升明显，且频率最大偏移量也有较大程度降低。

3）分布式控制提高了各区域的协同性。各区域频率变化趋势具有一致性，降低差异性，同时保证了区域间有功功率的互济。