关于简谐运动周期与机械波波速计算的教学思考——基于中日高中物理教材的比较

张明硕 于 佳,2 黄致新 吴春晓,3

(1.华中师范大学物理科学与技术学院,湖北 武汉 430079; 2.华中科技大学附属中学,湖北 武汉 430074;3.成都市第七中学,四川 成都 610041)

教材是学生获取科学知识、掌握科学方法的直接来源,是教师提取教学内容、设计教学思路的重要基础.在面对教学中的疑难问题时,综合考量不同教材的内容来设计教学过程,或许就能够寻求到突破疑难问题的方法.因此,本文选取我国广泛使用的人教版高中物理教材[1]以及日本物理教师几乎人手一本的高中物理教材《川胜教授的中学物理教案》[2]为研究对象,以简谐运动周期与机械波波速的计算问题为例,展开了对比研究,并提出了相应的教学建议.

1 中日高中物理教材简谐运动周期计算相关内容的研究

1.1 中国教材简谐运动周期计算的内容梳理

在我国人教版教材中,涉及简谐运动周期计算的内容分布在选择性必修第1册“机械振动”一章下的“简谐运动的描述”和“单摆”两节.

在“简谐运动的描述”一节,教材首先给出了做简谐运动的物体的位移x与运动时间t的关系,即正弦函数关系x=Asin(ωt+φ).随后给出了周期的定义,即做简谐运动的物体完成一次全振动所需要的时间,并根据正弦函数的规律,相位(ωt+φ)在每增加2π的过程中,函数值x循环变化一次,计算[ω(t+T)+φ]-(ωt+φ)=2π,解出ω=2π/T,可得T=2π/ω,其中ω叫作简谐运动的“圆频率”.在得到周期的计算方法之后,教材在“做一做”栏目给出了实验“测量小球振动的周期”,定性地得出了结论,弹簧振子的振动周期与其振幅无关,并且说明所有简谐运动的周期均与振幅无关.

在“单摆”一节,教材从回复力的角度证明了“在摆角很小的情况下单摆的运动可看成是简谐运动”.

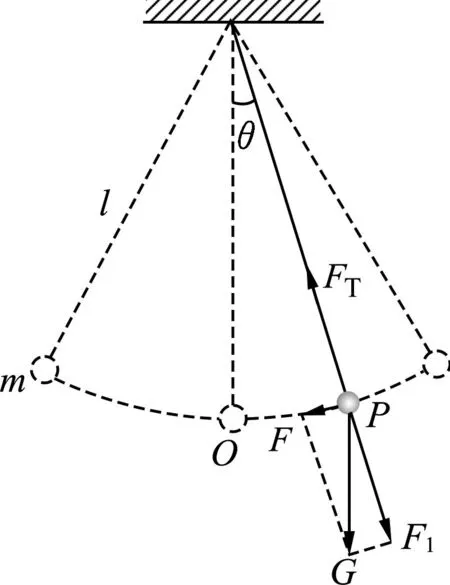
图1 单摆的回复力

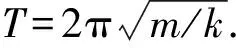
在数学教材中,[4]三角函数是利用圆来引入的.在简谐运动中,ω叫作简谐运动的“圆频率”,大小不变;而在匀速圆周运动中,ω表示角速度,完成一次匀速圆周运动所需时间也可通过“T=2π/ω”进行计算.学生在此不禁会思考,为何简谐运动周期的计算方法“T=2π/ω”在匀速圆周运动中同样适用,换言之,简谐运动与匀速圆周运动是否存在某种内在联系呢?

在大学阶段,可以利用简谐运动的合成,得到结论“振动方向垂直、振幅相等、频率相等,相位差为π/2的两简谐运动合成后的结果为匀速圆周运动”,从而说明简谐运动是匀速圆周运动的分运动.

那么在中学阶段,如何论证匀速圆周运动与简谐运动的关系,又是否可以从匀速圆周运动求出简谐运动周期的计算公式呢?

1.2 日本教材简谐运动周期计算的内容梳理

在日本教材《川胜教授的中学物理教案》中,涉及简谐运动周期计算的内容分布在第4章“振动与碰撞”下的第42讲“简谐运动的周期”和第43讲“各种各样的简谐运动”之中.

在“简谐运动的周期”一讲,教材根据简谐运动和匀速圆周运动的数学表达式,在数学上说明“简谐运动是匀速圆周运动的投影”,随后从匀速圆周运动出发,如图2所示,展开了对简谐运动周期公式的推导.

图2 简谐运动与匀速圆周运动的关系

F为向心力,r为运动半径,θ为相位.向心力大小为mω2r,质点m在x轴上的投影相对于圆心O的位移x为rcosθ.

分析向心力在x轴方向上的分量,可得Fx=-mω2rcosθ,用常量K代替mω2,x代替rcosθ,则Fx=-Kx,负号表示向心力分量Fx方向与位移x方向相反.在回复力与位移的关系上,匀速圆周运动在x轴方向上的投影与简谐运动一致,向心力分量Fx扮演了回复力的角色,K则为回复力系数.

在此需要向学生强调,正是“向心力分量Fx与位移x满足做简谐运动的物体所受回复力与位移的特点”这一事实,给 “简谐运动是匀速圆周运动的投影”这一数学结论提供了物理支撑.

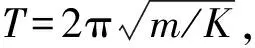
2 中日高中物理教材机械波波速计算相关内容的研究

2.1 中国教材机械波波速计算的内容梳理

为了计算机械波波速,就先需要理解什么是机械波,知道波的形成过程.

人教版教材将波定义为振动的传播,而机械波是指机械振动在绳、水、空气等介质中传播而形成的波.

教材以绳上的横波为例,展示了波的形成过程.设想把一条绳子分成一个个相连的质点,质点之间存在着弹性力.当手握绳端上下振动时,绳端带动相邻的质点上下振动,这个质点又带动更远一些的质点,以此类推绳子上的质点都跟着振动起来,绳端振动的状态也就沿着绳子这一介质传播开来,整体上形成了凹凸相间的波形.

结合具体的时刻分析,如图3所示,质点P0上下振动,依次牵动其余质点振动.在t=T/4时刻,质点P0向上到达了最高点,P2刚要开始运动.质点P0到达最高点后又开始下落,当t=T/2时,它又回到平衡位置,而这时P2刚刚到达最高点,质点P4则刚要开始运动,以此类推可以得到3T/4、T时刻各质点的位置及波的形状.

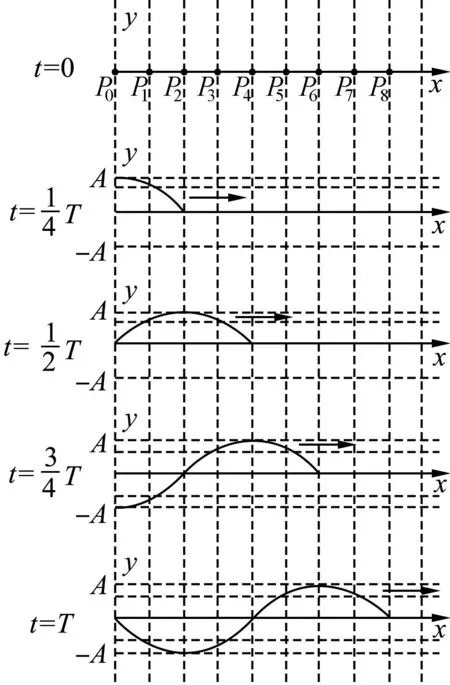
图3 绳上横波的形成

在对各时刻质点振动状态的分析中,其实已经隐含了波传播距离和传播所需时间的信息.根据波形图可知,在T时刻,质点P0与P8的振动状态相同,都是即将向上振动,那么波长就是质点P0与P8之间的距离.换言之,经过一个周期T,P0的振动状态在绳上传播了一个波长λ的距离到达了P8,波传播的速度即为v=λ/T.随后,教材说明“机械波在介质中的传播速度由介质本身的性质决定”,在不同的介质中,波速是不同的,并指出声速还与温度有关.

通过以上梳理可见,人教版教材给出了波速的计算方法v=λ/T.关于波速的影响因素,教材指出声波波速与温度有关,而对于其他类型的机械波的波速,教材则较为笼统地用“由介质本身的性质决定”进行了概括.

根据人教版教材的内容展开教学,学生能够利用v=λ/T计算出波速,但也会疑惑波速的影响因素到底有哪些;知道“组成介质的质点之间有相互作用,一个质点的振动会引起相邻质点的振动”,所以可能会提出猜想,认为波速与介质上质点间的相互作用也就是力有关,但不能给出清晰的解释,也难以推导出相关的波速公式.

关于机械波波速的影响因素,以图3所示的绳上的简谐波为例,根据大学阶段的物理知识,可利用简谐波的运动学方程y(x,t)=Acosk(vt-x),分别求方程对时间t和对坐标x的二阶偏导数,整理得到波动方程

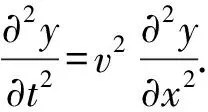
(1)

拉紧的绳上存在张力,结合牛顿第二定律与极限思想,[5]可以推导出波动方程的另一种形式,即

(2)

其中F为绳上张力的大小,ρ为绳的线密度.

2.2 日本教材机械波波速计算的内容梳理

日本教材也将波定义为运动状态的传播,并指出波的传播需要介质.关于波的产生机制,日本教材也是从介质之间的相互作用展开论述的.如图4所示,给予静止的弹簧一个扰动,箭头方向为质点所受回复力的方向,A点即将向下运动,B点与C点向上运动,随后带动D点与E点运动,以此类推,各质点依次运动,也就形成了波.

图4 弹簧上的扰动

解释了波的传播过程之后,教材开始求解绳波的波速.如图5所示,原本静止的绳,绳的一端以一定的速度u向上运动一段很小的时间t,波的传播速度为v,经过时间t波传播到了B点,AB段绳的线密度为ρ,在A点,绳与地面夹角为θ,绳子上的张力为T.

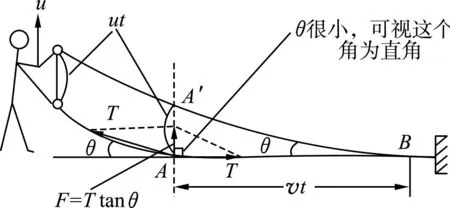
图5 绳波的波速

AB段的质量为ρ(vt),AB段上各质点获得的速度为u,受力的冲量为Ft,根据动量定理,可知

Ft=ρ(vt)u.

(3)

此时,以质点A为受力对象,当θ很小时,水平方向的合力为T-Tcosθ=0,竖直方向的合力为Tsinθ=Ttanθ.从图中我们可以看出,tanθ=ut/(vt).结合以上分析可以得出,AB段所受合力为

(4)

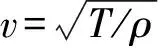
3 教学启示

3.1 注重前后知识的关联

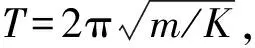
因此,在教学时应注重对各知识点之间关系的把握.结合前后所学内容,推动学生将较为分散的知识点转化为较为完善的物理观念,深化学生对物理概念的理解.

3.2 聚焦物理公式的本质

因此,教学要聚焦物理公式的本质含义.在分析具体的物理实例时,应从物理本质出发,进行演绎推理,以此实现物理公式在不同物理情景下的迁移应用.

3.3 渗透大中衔接的内容

因此,中学物理教学要关注大学物理与中学物理的衔接问题.[6]大学物理与中学物理并不是完全平行与割裂的,在本文公式的推导过程中,大学物理既有大学阶段的新方法,也有中学物理的旧知识.在教学中寻求合适的教学内容,在中学物理的范畴得出大学物理的结论,既是对中学物理教学的深化,也是对学生在大学阶段的物理学习进行的预热,有利于学生实现从中学物理到大学物理的平稳过渡与顺利进阶.

4 结语

对比分析不同国家的教材,可以开阔教学视野,[7]拓展教学思路,丰富教学资源.关于如何计算简谐运动周期与机械波波速,中日教材给出了不尽相同的思路与方法.面对学生的疑问,教师可以综合考量两国教材的内容,阐明物理知识之间的联系,把握计算公式的物理本质,渗透与大学物理的衔接内容,结合学生的认知情况设计合适的教学方案,切实解答学生疑惑,满足学生求知欲望,激发学生探索物质世界的兴趣.