学会思维:赋能物理高考关键能力

王 高

(江苏第二师范学院,江苏 南京 210013)

古人云:善学者,师逸而功倍;不善学者,师劳而功半.新时代物理教师教学中落地核心素养,不仅要帮助学生“学会”知识和方法,更要促进学生“会学”,就是说要学生学会思考,成为“思考能人”,以充分发展智能,培养关键能力.

物理高考关键能力包括:理解能力、推理论证能力、模型建构能力、实验探究能力和创新能力.仔细分析可以发现:理解能力与“物理观念”紧密相关,是物理概念、规律的深度理解与迁移应用;推理论证能力是“科学推理、科学论证”在问题解决中的综合体现;模型建构能力是在“模型建构”的基础上形成的重要思维能力;创新能力是以“质疑创新”为基础的高阶思维能力;实验探究能力是物理实验与科学探究深度整合的实践思维能力,如图1所示.可见,物理高考关键能力与学科核心素养的价值指向是一致的,其中科学思维是关键能力的核心.

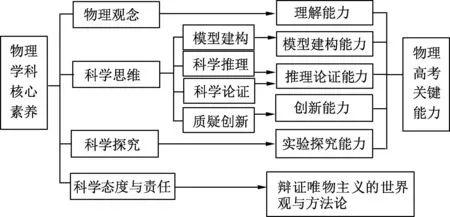
图1 物理核心素养与高考关键能力之间的关系

新时代的物理教学要求以核心素养为目标,而高考聚焦关键能力考查、突出思维品质与创新精神.对于学生而言,提高高考关键能力是最重要的任务.《礼记·中庸》中描述的求知过程是:博学之,审问之,慎思之,明辨之,笃行之.审问、慎思、明辨、笃行的核心是学会思维,学会思维赋能物理高考关键能力.

1 学会审问,激活思维

杜威指出:思维是从直接经验的情境中产生的,思维的目的和结果都是由产生思维的情境决定的.情境是激发学生思维的载体,物理知识的生成与应用都是基于真实情境的.教师要训练学生从试题情境审问、思考、分析中,抓住情境背后的物理本质,清晰其中蕴含的物理原理,并与已知的、熟悉的物理试题形成良好的链接.增强学以致用和活学活用的力度,培养学生分析解决实际问题的能力,实现从“解题”到“解决问题”的转变.

例1.(2023年江苏高考第10题) 达·芬奇的手稿中描述了这样一个实验:一个罐子在空中沿水平直线向右做匀加速运动,沿途连续漏出沙子.若不计空气阻力,则图2中能反映空中沙子排列的几何图形是

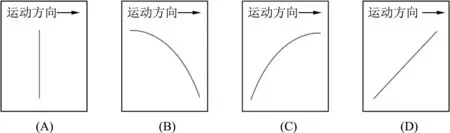
图2 空中沙子排列情况

解析:达·芬奇的实验创设了一个真实的问题情境,但学生熟悉的是某一物体在一段时间内的位置分布,即轨迹,而题中问的是同一时刻空中沙子排列的几何形状,比较陌生.教师可引导学生从熟悉的运动情境飞机水平匀速飞行时投弹情况(如图3)入手,进而思考当飞机水平匀加速飞行时

图3 飞机匀速飞行投弹

投弹情况(如图4):沿水平方向向右做匀加速运动,竖直方向做自由落体运动,则水平方向位移增加量与竖直方向位移增加量比值一定,连线的倾角是一定的,答案为(D).这里就是模型迁移的思维方法应用,提升了学生理解能力、模型建构能力和推理论证能力.

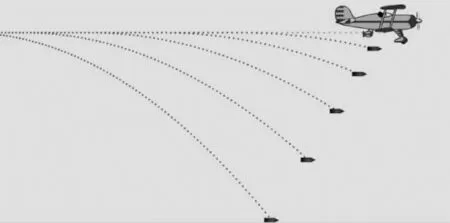
图4 飞机匀加速飞行投弹

2 学会慎思,进阶思维

思维或思考不仅是一种能力,也是一种超越知识的价值取向.思维方法好似一只“看不见的手”,始终“牵引”着学生的物理学习.挖掘和应用思维方法可以解决“怎么做”的问题.培养综合批判性思维、创造性思维和解决问题的能力,所以,教师的使命在于有意识地渗透思维方法并智慧地应用,帮助学生解题悟道,启智增慧,在面对真实、陌生的问题解决中得心应手.

例2.(2022年全国高考甲卷第21题)地面上方某区域存在方向水平向右的匀强电场,将一带正电荷的小球自电场中Р点水平向左射出.小球所受的重力和电场力的大小相等,重力势能和电势能的零点均取在Р点(如图5).则射出后

图5 小球在电场中运动

(A) 小球的动能最小时,其电势能最大.

(B) 小球的动能等于初始动能时,其电势能最大.

(C) 小球速度的水平分量和竖直分量大小相等时,其动能最大.

(D) 从射出时刻到小球速度的水平分量为零时,重力做的功等于小球电势能的增加量.

解析:题中对于小球的运动需要学生分析题意构建出运动模型——类斜抛运动模型,再利用模型遵从的规律推理分析,进而实现问题的解决,培养学生的模型建构能力、推理论证能力.

带电小球受到水平向右的电场力和竖直向下的重力作用,如图6所示,且Eq=mg.故等效重力G′的方向与水平方向成45°.

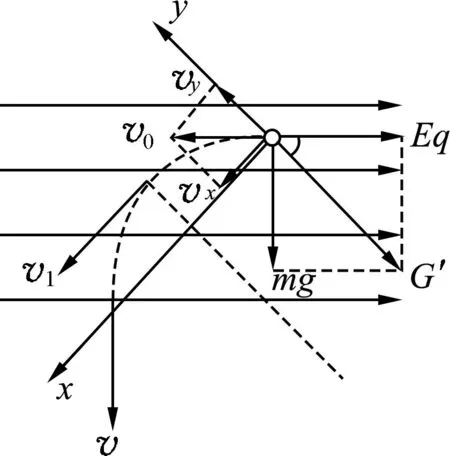
图6 小球在电场中的受力分析图

当vy=0时速度最小为vmin=v1,由于此时v1存在水平分量,电场力还可以做负功,故此时电势能不是最大,故(A)错误.

当速度为v1时,速度水平分量与竖直分量相等,动能最小,故选项(C)错误.

教学中教师应从“授鱼—授渔—学渔”转变,学渔就是学会思维,善于灵活选用思维方法(如本题中的转化法)分析、解决问题,实现了从知识立意走向关键能力立意的转变,实现从低阶思维向高阶思维的进阶.

3 学会辨析,理性思维

学会思维的重要作用是提高人的理性精神,具有理性精神的人一般不会盲目跟着感觉走,遇事会多问几个为什么,努力透过现象看清本质,既不盲从,也不迷信权威,坚信让实验说话、逻辑思维、推理有据的理性精神.让学生从自然状态的思考走向善于思考、科学思考,能根据已有的事实质疑、推理、论证和解释,使理性思维成为一种习惯.杜威说过,教育在理智方面的任务是形成清醒的、细心的、透彻的思维习惯.

例3.(2019年北京高考第21题)牛顿设想,把物体从高山上水平抛出,速度一次比一次大,落地点就一次比一次远,如果速度足够大,物体就不再落回地面,它将绕地球运动,成为人造地球卫星.

同样是受地球引力,随着抛出速度增大,物体会从做平抛运动逐渐变为做圆周运动,请分析原因.

解析:平抛运动与匀速圆周运动模型学生都很熟悉,但是对于它们之间的联系与区别缺少深度思考,认识不够清晰,本题将两种模型置于熟悉的“牛顿大炮”情境中,考查学生的理解能力、模型建构能力、推理论证能力和创新能力.

水平抛出物体的初速度较小时,运动距离很小,引力可以视为恒力——重力,此时物体做平抛运动;随着抛出的初速度增大,运动空间范围变大,引力不能再看作恒力了;当物体初速度达到第一宇宙速度时,则做圆周运动而成为地球卫星,此时的引力提供物体做圆周运动的向心力——方向时刻在变化.

分析中关键是要领悟两种变化.

量变:速度增大——万有引力从恒力(重力)变为变力(提供向心力).

质变:运动性质变化——从平抛运动(匀变速曲线运动)变为匀速圆周运动(变加速曲线运动).

这里,物理问题解决中运用了辩证思维,能进一步加深学生的理解.

我们再来研究匀速圆周运动向心加速度公式推导的另一种思路,如图7所示.

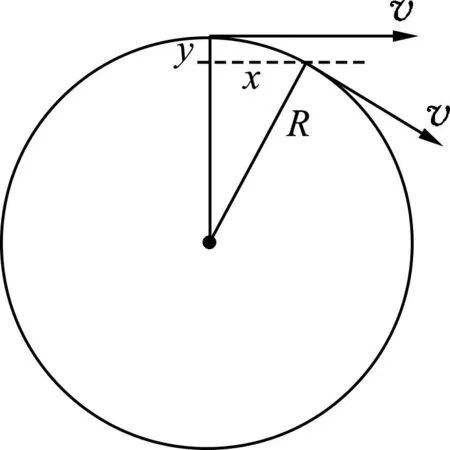
图7 匀速圆周运动分析图

对于平抛运动取一个很短时间Δt,则有

x=vΔt.

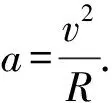
平抛运动与匀速圆周运动是不同性质的运动,但在一定条件下(极短时间内)又是统一的,我们要学会应用联系的观点去分析、解决问题.

在培养学生理性思维时,可以按照《论语》中的“勿意、勿必、勿固、勿我”来要求.勿意——做事不能凭空猜测主观臆断,一切以事实证据为依据.勿必——对事物不能绝对肯定或否定,要有辩证思维.勿固——不能拘泥固执,要灵活善变.勿我——不要自以为是,要善于理性思考.

例4.(2022年上海高考第6题)运动员滑雪时运动轨迹如图8所示,已知该运动员滑行的速率保持不变,角速度为ω,向心加速度为a,则

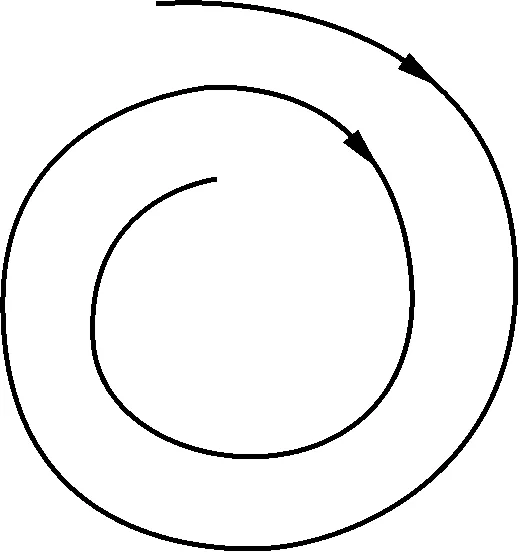
图8 运动员滑雪轨迹

(A)ω变小,a变小.

(B)ω变小,a变大.

(C)ω变大,a变小.

(D)ω变大,a变大.

解析:由题意可知,运动员滑行的速率不变,做匀速率曲线运动,轨迹很像螺旋线,不是学生熟悉的圆周运动,给学生的分析带来一定的困难.需要突破思维,构建出合理的物理模型,考查学生模型建构能力、推理论证能力和创新能力.

从运动员短时间运动来看,轨迹接近圆弧,可近似为圆周的一部分,所以,运动员的运动在短时间内可视为匀速圆周运动.

根据v=ωr可知,r减小,角速度ω增大;根据向心加速度公式a=v2/r可知,r减小,向心加速度变大,选项(D)正确.

通过微元法分析运动员的运动,发现在短时间内运动员的运动可视为匀速圆周运动,进而建构了匀速圆周运动模型.将运动员的运动视为匀速圆周运动需要大胆质疑,是思路可行的.

教师通过营造思维场,引发学生思维需求,通过深度学习、质疑反思等方式,鼓励学生大胆质疑,培养批判精神和创造性思维,提高分析问题和解决问题的能力.

4 学会迁移,升华思维

学会思维不仅要强化思维内涵的理解,还要在迁移应用中培养创新精神和实践能力,不断升华思维,实现学科育人的价值.

例5.(2016年全国高考新课标卷第16题)一含有理想变压器的电路如图9所示,图中电阻R1、R2和R3的阻值分别为3 Ω、1 Ω、4 Ω,A为理想交流电流表,U为正弦交流电压源,输出电压的有效值恒定.当开关S断开时,电流表的示数为I;当S闭合时,电流表的示数为4I.求该变压器原、副线圈匝数比.

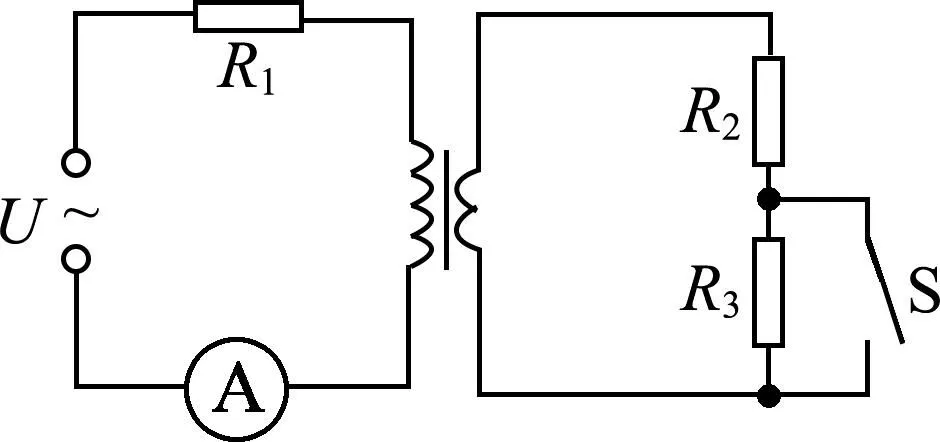
图9 理想变压器电路

解法1:解析法.

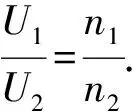
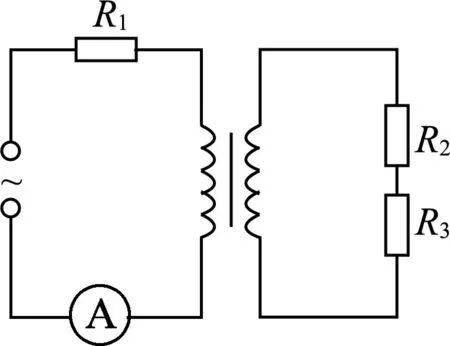
图10 S断开时电路

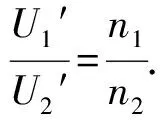
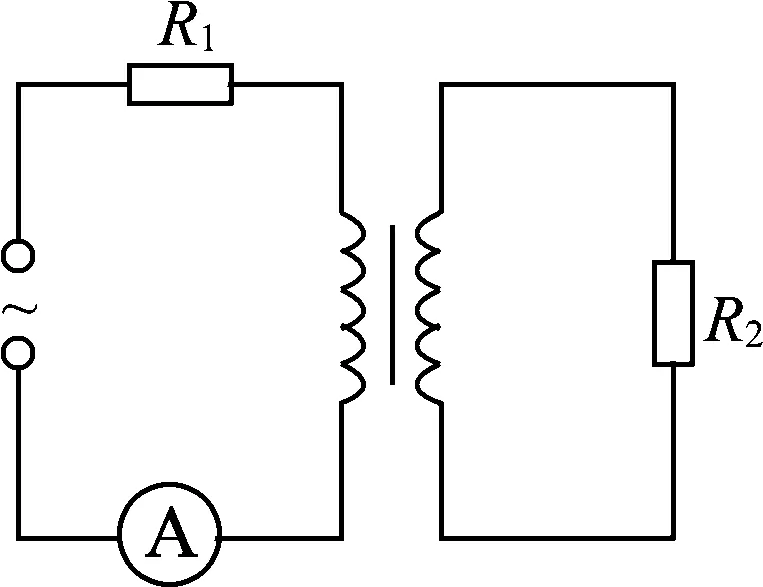
图11 S闭合时电路

解法2:等效电阻法.

将变压器和负载等效为一个电阻R′,如图12所示.

依据题意有

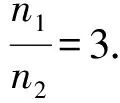
高考关键能力是核心素养的价值体现,真实情境是关键能力考查的载体,教师通过情境设计,让学生思维放飞,在思考、应用、迁移中学会思维,提高物理关键能力.