试论科学思维素养之模型建构要素的实质与培养

陈 刚

(华东师范大学教师教育学院,上海 200062)

科学思维素养是物理学科核心素养组成成分,科学思维素养包含:模型建构、科学推理、科学论证、质疑创新等要素.关于模型建构“在物理学中,突出问题的主要因素,忽略次要因素,建立理想化的物理模型,并将其作为研究对象,是经常采用的一种科学研究方法”.[1]关于模型建构的教学建议:教师在教学中要让学生体会建构这些物理模型的思维方法,理解物理模型的适用条件……,教师引导学生经历物理概念的建构过程和物理规律的形成过程是发展科学思维的重要途径.[2]

从以上描述,我们可以了解到模型法是一种科学研究方法,那么

问题1:构建物理模型过程中有哪些基本思维方法?

问题2:如何引导学生经历物理概念的建构过程,从而达成培养学习者模型建构能力的目标?

从学习者角度,模型建构显然是一个解决问题的过程.本文以问题解决相关研究对上述问题做出回答.

1 问题解决

认知心理学提出:问题解决是解决者运用认知策略从认知结构中选择出解决问题所需必要技能的过程.[3]

因此,问题是否能得到解决,取决于:其一,问题解决者是否具备解决问题的必要技能;其二,问题解决者是否具备解决问题的策略.

认知策略是提高问题解决效率的技能,是面对待解决的问题时,引导个体思考方向以选择出并组合解决问题所需技能的技能.[4]解决问题的原则、途径、环节、要素、思路、方法等,都是提高解决问题效率,从认知心理学视角,它们都属于认知策略这一类学习结果,只是解决问题的效率存在差异,有些属于解决问题的弱方法,有些属于解决问题的强方法.[4](因为方法、策略属于同一类学习结果,以下不做区分.)

认知策略的操作对象是个体已习得的、存储于内部认知结构中的知识(广义的知识,包含陈述性知识和程序性知识),因而,认知策略是对“内”操作的技能;又因为认知策略是对解决问题所需必要技能的选择、组合,因此,外显可以表现为引导解决者思考方向的步骤.

如运用“惯性”概念解释日常生活现象的方法,其一般步骤为:(1) 明确研究对象; (2) 确定研究对象原先处于的状态;(3) 突然发生何种变化;(4) 由于存在惯性,研究对象要保持原有状态;(5) 出现什么现象.

当学习者面对需要运用惯性概念解释现象的问题时,上述步骤,可以引导学习者的思考方向,从认知结构中逐一选择出解决该问题所需的技能,提高学习者解决“惯性运用类”问题的效率.

2 模型建构素养的实质

2.1 模型建构的过程

在学习中,个体如何建构物理模型呢?本文以杠杆模型的建构为例,尝试做出解释.

日常生活和生产中有许多运用杠杆的场合,如图1所示.从图1中杠杆情境到最终概括出杠杆模型,如图2所示,即模型建构的过程.

图1 各种杠杆

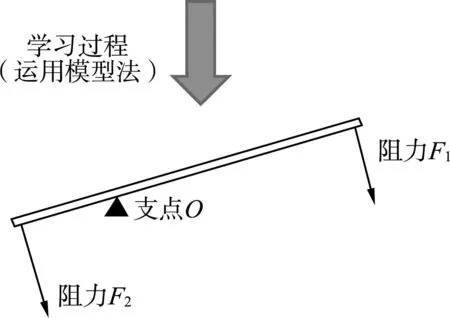
图2 杠杆模型

追寻学习者杠杆模型建构过程,大致可能经历如下几个阶段.

2.1.1 学习者面对杠杆的实际情境

学习者面对如图1所示实例.

2.1.2 学习者概括杠杆基本工作特征

问题:学习者如何从如图1所示多个实例中提取出杠杆的基本特征?

从多个实例中,概括出杠杆这类对象的共性特征,实际需要学习者形成本课例“研究对象”与“工作的基本特征”间的联系.

(1) 解决问题的机制.

个体形成两个因素间的因果联系的方法是逻辑的,主要有归纳推理中的求同法、差异法、求同求异法、共变法等.

[求同法] 求同法是通过考察被研究现象出现的若干场合,确定在各个场合先行情况中是否只有另外一个情况是共同的,如果是,那么这个共同情况与被研究的现象之间有因果联系.其结构可以如表1所示.

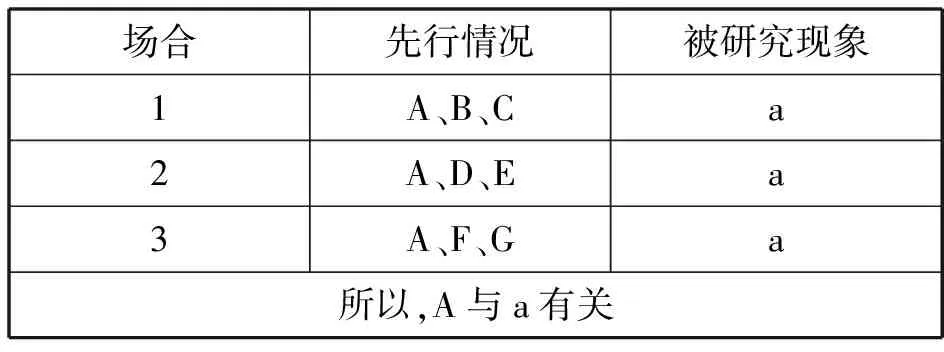
表1 求同法的结构

(2) 本例确定杠杆工作特征所运用的方法.

本例中通过3个实例,概括出待研究的对象,是通过运用求同法实现的,如表2所示.

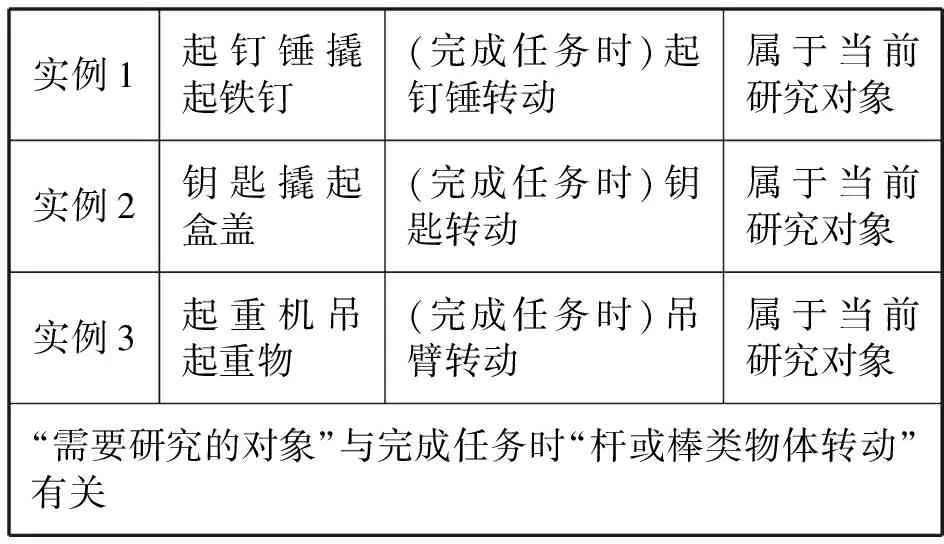
表2 求同法概括研究对象

此类,通过杆或棒类物体转动完成任务的工具(简单机械),即杠杆.

2.1.3 学习者明确杠杆的主要因素

问题:学习者如何确定研究对象的主要因素?

主要因素是研究对象必不可少的因素.从学习角度,同样需要学习者形成待研究对象与相关因素间的因果关系.

(1) 解决问题的机制.

[差异法] 差异法是通过考察被研究现象出现和不出现的两个场合,确定在这两个场合中是否只有另外一个情况不同,如果是,那么这个不同情况与被研究现象之间有因果联系.其结构可以如表3所示.

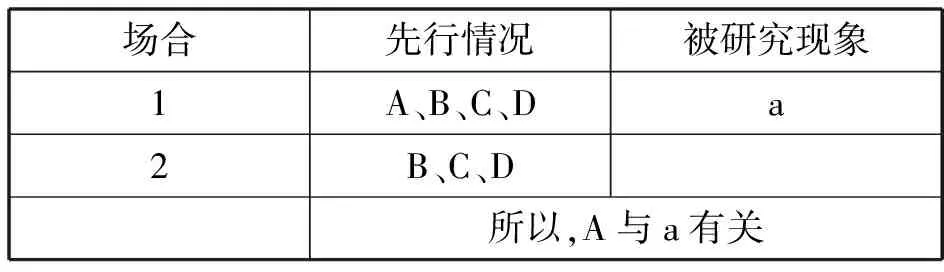
表3 差异法的结构

[求同求异法] 求同求异法是考察两组事例,一组是由被研究现象出现的若干场合组成的,称为正事例组;一组是由被研究现象不出现的若干场合组成的,称为负事例组.如果在正事例组的各场合中只有一个共同的情况并且它在负事例组的各场合中又都不存在,那么,这个情况就是被研究现象的原因.其结构如表4所示.

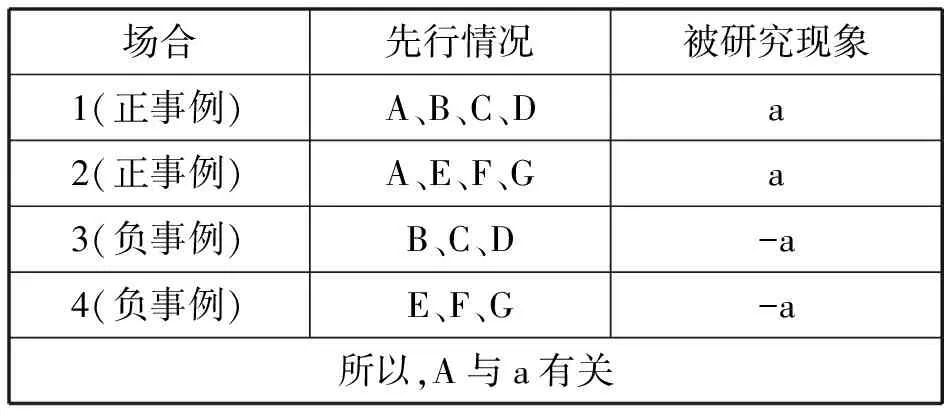
表4 求同求异法的结构

(2) 本例确定杠杆的主要因素所运用的方法.

① “杠杆”与“受两类转动效果相反的力”有关,如表5所示.

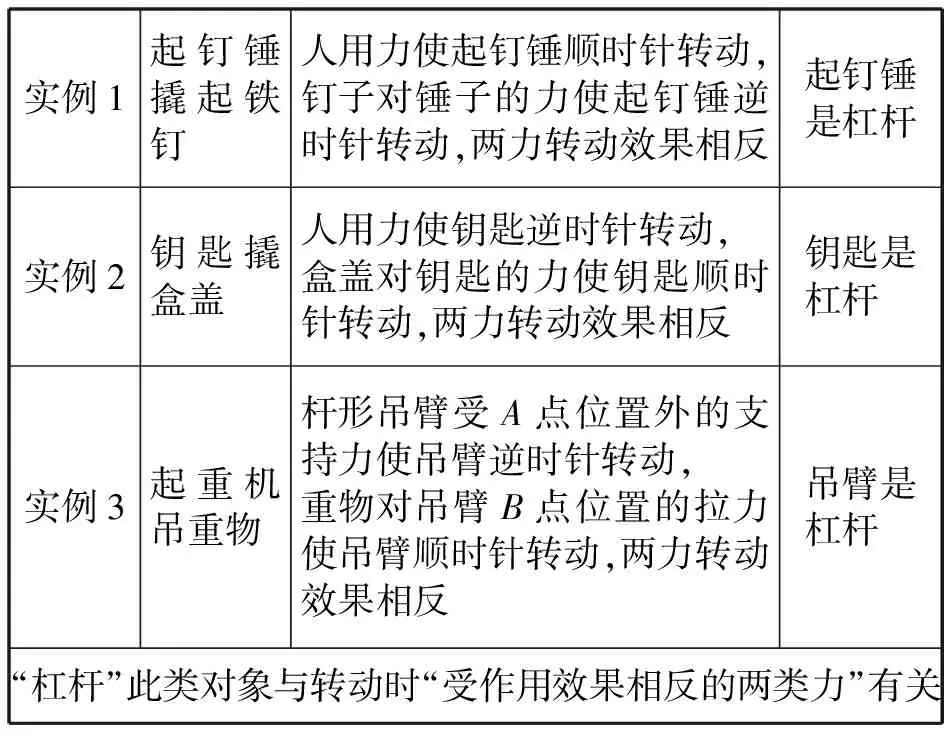
表5 求同法概括杠杆模型的主要因素

② “杠杆”与完成任务时棒的“硬”有关.

在教学中,为了突出杠杆需要棒“硬”,提供如下实例.

实例1:用钥匙撬盒盖,钥匙转动撬起盒盖,此时钥匙是杠杆.

实例2:用吸管撬盒盖(如图3),吸管已变形,无法转动撬起盒盖,吸管不是杠杆.

图3 吸管撬盒盖

实例3:用吸管挑出杯中的柠檬片,吸管尽管有变形,仍完成将柠檬片挑(即撬)起,此种情况下吸管是杠杆.

通过以上3个实例,学习者识别出有效信息,遵循求同求异法形成“杠杆”此类简单机械与棒在使用时的“硬”有关系,结构如表6.

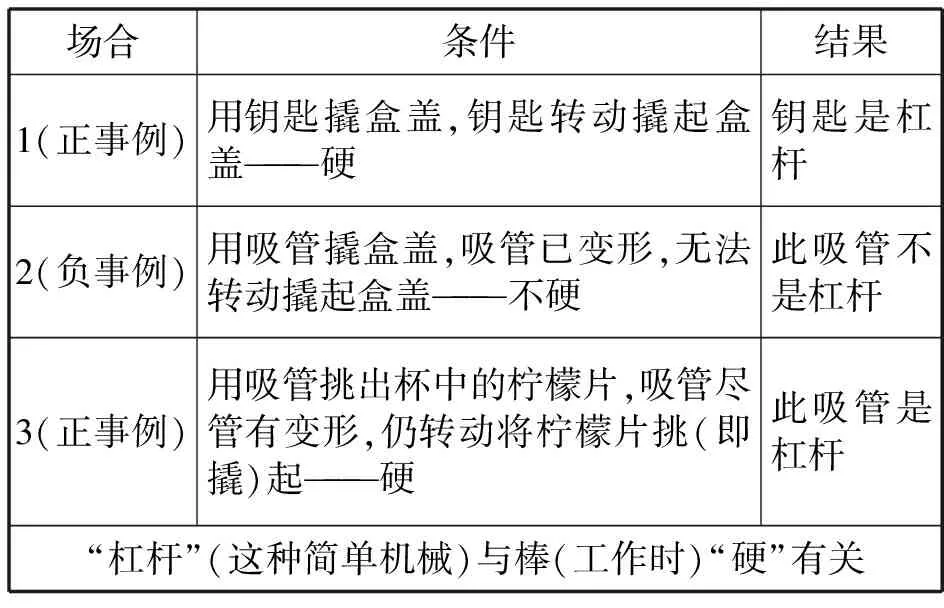
表6 求同求异法概括杠杆模型的主要因素

2.1.4 学习者明确杠杆的次要因素

问题:如何确定待研究对象的次要因素?

次要因素是指在引起结果发生的诸因素中起非主导和非决定作用的因素.简言之,次要因素与结果的发生与否不存在必然关系.

(1) 解决问题的机制.

物理概念和规律学习过程中,除了要形成物理概念间存在定性、定量的因果关系,往往还需要排除两个因素间不存在因果联系.

排除两个因素间不存在因果关系,是通过以因果关系为大前提的演绎推理实现的.

因果关系归结为:等价的原因→等价的结果.

由此,可以获得两种前提:

前提1:如果本质原因存在,则结果也应存在.

前提2:如果本质原因改变,则结果也应变化.

以此为前提,可有两种排除物理量因果联系的演绎推理方式.

推理形式1:

如果A与B有因果联系,则A变化,B亦变化.

推理形式2:

如果A与B有关,则A不变化,B亦不变化.

(2) 本例确定排除杠杆次要因素运用的方法.

① 形状不是杠杆的主要因素.

如图1所示案例中,有直形棒、弯形棒,都属杠杆.

如果A与B有因果联系,则A变化,B亦变化.

② 材质也不是杠杆的主要因素.

因为材质不同,如吸管挑起柠檬片、钥匙撬起盒盖,它们都是杠杆.如同前述的演绎推理,可知材质不是杠杆必不可少的因素,即为次要因素.

2.1.5 学习者概括出杠杆模型

在分析出杠杆的主要因素、次要因素后,可忽略形状、材质等次要因素,突出工作时杆或棒绕点转动、受两类转动效果不同的力等主要因素,概括出如图2中的杠杆模型.

2.2 模型建构的实质

模型建构本质上是学习者解决问题的过程.解决此类问题,也存在有助于提高解决者完成此项任务的策略或者说方法.结合杠杆模型建构过程,可提出物理概念和规律学习中的模型法.

物理概念和规律学习中的模型法:通常用在提出问题环节.若需抽象物理模型,其基本步骤为

(1) 从具体情境中初步确定待研究对象;

(2) 确定待研究对象以及属性(通常用求同法等);

(3) 分析待研究属性出现的必要条件(通常用差异法、共变法、求同法、求同求异法等);

(4) 分析待研究属性的次要因素(通常用排除因果联系的逻辑方法等);

(5) 突出主要因素、忽略次要因素,概括待研究的物理模型.

如果在物理课程学习中,当学习者面临问题:如何抽象物理模型?上述步骤(1)～(5)可以帮助学习者有序地进行思考,避免低效率的盲目思考.

如果进一步追问:如何分析出待研究对象的主要因素?括号中相对具体的逻辑方法,又可以给予学习者一定思考方向,助力学习者解决这一子问题.

所以,模型建构是在不同层次方法引导下解决问题的过程.在物理课堂学习中的抽象模型,大体上可以运用上述方法加以解决.

以上为对问题1的回答.

此处模型法揭示出课堂学习中形成研究对象共性特征、概括研究对象主要因素、排除研究对象次要因素等可用的逻辑方法,相较于文献[1]描述性的界定,可以帮助学习者更好地理解模型法用在何处以及如何运用.

3 模型建构的培养方案

如果模型建构要求学习者经历运用模型法抽象物理模型的过程,那么实际教学中,教师就应该遵循模型法的步骤,引导学习者经历模型化的每一子过程,并在每一子环节中引导学生识别相应结论获得的有效信息(根据结论获得逻辑结构),帮助学生最终抽象出物理模型.

例如杠杆模型建构的教学(如表7所示)中,学生在形成“杠杆这类对象与棒转动中受两种相反作用效果的力”有关时,是运用求同法实现的,所以,教学中应遵循求同法的逻辑结构以及信息呈现方式,引导学生依次识别共同结果(步骤4,确定3个实例中的杠杆)、共同条件(步骤 5～6引导学生完成受力分析,为转动效果分析提供必要信息;步骤7引导学生识别共同条件),并引导学生形成共同结果和共同条件间的联系(步骤8,将杠杆与受转动效果两类力形成因果联系).

表7 杠杆模型建构的教学

以上教学步骤并不严格僵化,实际教学中,是引导学生先分析次要因素再分析主要因素,或先分析杠杆与“硬”的关系还是先分析杠杆与“受转动效果”不同两类力等,这都是可选择的,但整体都应包含模型法的各子步骤,每一具体子结论的获得应遵循结论获得的逻辑结构.

以上是针对问题2的回答.

经过运用模型法抽象物理模型的教学,学习者能够表现出从实际情境中有逻辑地抽象研究对象的基本属性、能够有序识别并有逻辑地确定研究对象存在的主要因素以及次要因素,进而忽略次要因素,突出主要因素,概括出待研究的物理对象,从而一定意义上达到培养学习者模型建构能力的目标.