透过现象看本质 切忌教条学方法——由一道中考试题谈控制变量法

朱文军

(江苏省教育科学研究院,江苏 南京 210013)

1 提出问题

浮力的大小与物体浸入液体中的深度是否有关,要分成两种情况进行讨论.当物体浸没后,浮力的大小与物体浸入的深度无关,这种情况实验操作简单、学生也容易理解;第二种情况是物体浸没前,这种情况一直困扰着很多师生,大家的观点很难统一.在2022年中考试题中就出现了这样一个有待商榷的试题.

(2022年某地中考试题)兴趣小组探究影响浮力大小的因素.

提出如下猜想.

猜想1:与物体浸在液体中的深度有关.

猜想2:与物体浸在液体中的体积有关.

猜想3:与液体的密度有关.

小组为验证上述猜想,用弹簧测力计、4个相同的小长方体磁力块、2个分别盛有水和盐水的烧杯等,按图1(甲)步骤进行实验:

图1 原题图

① 利用磁力将4个磁力块组合成长方体物块;

② 根据图A、B、C的测量结果,小明认为猜想1是正确的,小华却认为不一定正确.你觉得小华的理由是;

③ 小华为了证明自己的想法,利用上述器材设计实验D,根据A、B、D的测量结果,可得:浮力大小与物体浸在液体中的深度无关,请在图1-D中画出她实验时长方体物块的放置图.

题目给的参考答案是:②没有控制物体排开液体的体积相同.③如图2所示.

图2 答案图

笔者认为此题值得商榷.针对影响浮力大小的因素提出的猜想之间应该是相互独立的.根据题目给的实验器材,物体浸没前浸入的体积和浸入的深度之间存在V排=Sh的关系,V排和h不是相互独立的.

2 设计实验 遵循逻辑

为什么要用控制变量法?这是我们应该思考的一个问题.在传统逻辑的发展过程中遇到如何探究两个事物之间是否有因果联系的问题,弗兰西斯·培根最早做过研究,后经穆勒进行归纳总结,形成了溯因推理经常用到的“穆勒五法”,包括求同法、求异法、求同求异法、共变法和剩余法.“穆勒五法”是在长期的生产生活实践中概括总结出来的,得出的结论不具有必然性,而具有或然性.考查的情况越多,得出结论的可靠程度就越高.

2.1 求同法

求同法是指在某个事物A出现的若干场合中,都有唯一的相同情况a出现,则a和A之间很可能有因果关系.公式如表1所示.

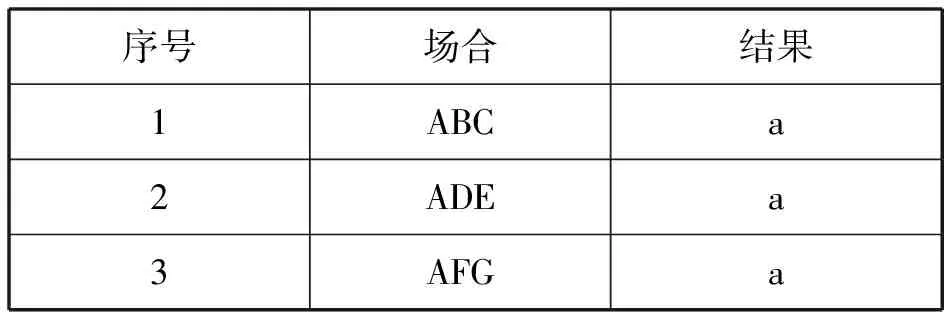
表1 求同法

则:A和a之间很可能有因果关系.

在探究声音是如何产生时,就可以用求同法来进行研究.把敲击后的音叉接触悬挂着的乒乓球,看到乒乓球被弹开(说明音叉在振动),同时听到音叉发声;被敲击的锣发声,用手摸发声的锣感觉到它在振动;在发声的音箱纸盆上放一些小泡沫球,看到小泡沫球上下跳动;说话时用手摸喉结,感觉到声带在振动……利用求同法,可以得出声音是由物体振动产生的.

2.2 求异法

求异法是指在某个事物a出现与不出现的两个场合中,只有唯一的不同(对应着A的出现与否),则a和A之间很可能有因果关系.公式如表2所示.

表2 求异法

则:A和a之间很可能有因果关系.

探究声音的产生条件也可以用到求异法.用敲击后的音叉接触悬挂着的乒乓球时,乒乓球被弹开(说明音叉在振动),同时听到音叉发声;用没有敲击的音叉接触悬挂着的乒乓球时,乒乓球没有被弹开(说明音叉不振动),也听不到音叉发声.得出声音是由物体振动产生的.

2.3 求同求异法

为了使结论的可靠程度更高,在进行溯因推理时会用到求同求异法.现象a出现和不出现的情况都有几种,这时可以在现象a出现的组内求同、现象a没有出现的组内也求同,两组之间求异.

2.4 共变法

在探究两个物理量之间是否有因果联系时,经常用到共变法.在被研究现象发生一定程度变化的各个场合中,如果其中只有一个情况(A)发生一定程度的变化,而其他情况保持不变,那么这个唯一变化的情况(A)很可能就是被研究现象(a)变化的原因(或结果),如表3所示.

表3 共变法

当学生提出滑动摩擦力的大小可能与压力和接触面粗糙程度有关时,应该分别研究接触面粗糙程度相同时滑动摩擦力大小是否随压力的变化而变化、压力相同时滑动摩擦力大小是否随接触面粗糙程度的变化而变化,从而根据现象得出结论.

在设计此实验时要用到控制变量法,在根据实验现象(数据)推理、论证得出结论的过程中要用到“穆勒五法”中的共变法.

2.5 剩余法

已知复合因素(A,B,C,D)是复合现象(a,b,c,d)的原因,又已知B是b的原因,C是c的原因,D是d的原因,那么剩下的A就是a的原因.

从中可以发现,在探究事物之间是否有因果联系时,在推理、论证的过程中无论用到“穆勒五法”中的哪一种方法,设计实验时都要用到控制变量法.求同法要求各个场合中相同因素只有一个;求异法要求各个场合中不同的因素只有一个;共变法要求变化的物理量只有一个;剩余法要求剩下的因素只有一个.

3 把握本质 用好方法

用控制变量法设计实验探究事物之间是否有因果联系,是用“穆勒五法”进行溯因推理的必然要求.首先要明确相同的因素或者不同的因素(物理量)只能有一个.

3.1 求同法中相同的因素要唯一

在探究电荷之间相互作用规律时,可以设计用相同方法摩擦(两根一样的玻璃棒与同一块丝绸摩擦、两根相同的橡胶棒与同一块毛皮摩擦、两根一样的吸管与同一个塑料袋摩擦、两个同样的梳子与同一位学生的头发摩擦等),现象是两个用同样方法摩擦的物体放在一起都相互排斥,各个场合的两个物体都是带同种电荷.根据求同法得出同种电荷相互排斥.当发现丝绸摩擦过的玻璃棒和毛皮摩擦过的橡胶棒相互靠近时吸引,根据“同种电荷相互排斥”可以得出玻璃棒和橡胶棒带的不是同种电荷,不是同种电荷就应该是异种电荷,进一步推理出异种电荷相互吸引.当后来遇到两个物体相互排斥时,根据“异种电荷相互吸引”可以知道这两个物体带的不是异种电荷,那就应该是同种电荷.同理,两个带电体相互吸引时,根据“同种电荷相互排斥”可以得出这两个物体带的不是同种电荷,那就应该是异种电荷.可以发现,“同种电荷”与“相互排斥”是等价的关系,也就是充分必要条件(充要条件);“异种电荷”与“相互吸引”也是充要条件.

3.2 求异法中不同的因素要唯一

“二力平衡”的教学逻辑顺序是由图片(视频)介绍平衡状态的定义、平衡力的定义、二力平衡的定义,然后请学生根据生活经验和课堂上的实验现象猜想二力平衡中的两个力要满足哪些条件.当学生提出大小相等、方向相反、作用在同一直线上这3个猜想(条件)时,就需要用求异法进行推理论证、控制变量法进行设计实验.可以做4次实验,第1次同时满足3个条件,后面3次每次只满足其中2个条件,实验过程和现象如表4所示.

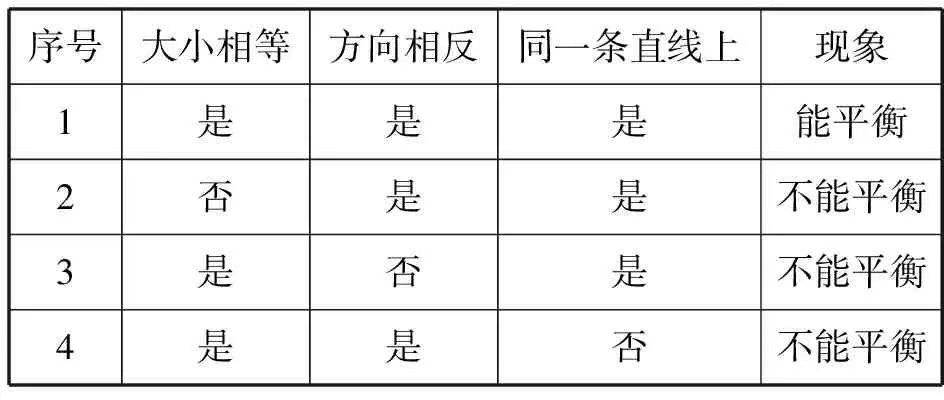
表4 “二力平衡”实验设计

比较实验2和1可以知道大小相等是必要条件;比较实验3和1可以知道方向相反是必要条件;比较实验4和1可以知道两个力在同一直线上也是必要条件.

第3次实验两个力在一条直线上方向不相反,学生很容易想到设计的实验要让两个力方向相同;第4次实验要求研究对象受到的两个力方向相反但不在同一直线上,学生经过思考会想到几何中学习的同一平面内两条直线的位置关系——平行,如图3所示.而图4和图5的设计方案都是错误的,这两种设计和第1次实验相比(求异)都有两个因素不同(既不共线也不反向),根据实验3和实验1求异得出的结论“方向相反是必要条件”,那不管“共线”是不是必要条件物体都不能保持平衡状态.

图3 卡片受力方向平行

图4 往下拉卡片

图5 向上拉卡片

顺便说明一下,探究二力平衡的条件实验无须探究两个力是否要作用在一个物体上,二力平衡的定义已经明确规定是一个物体只在两个力的作用下处于平衡状态.

有教师在A、B两个大试管中各装入50 mL常温水,用导管C把水蒸气导入试管B 中,发现试管B中的温度计示数上升,如图6所示,从而根据这个实验现象来说明液化放热,这种设计和推理逻辑上是错误的.我们可以假设液化既不放热也不吸热,由于液化成的100 ℃水比试管B中原来水的温度高,也会对试管B中的冷水放热,提高水温.

图6 希望说明液化放热实验装置

3.3 共变法中变化的物理量要唯一

研究弦乐器的音调与哪些因素有关,是中学物理教学中最先用到控制变量法设计实验、用共变法推理的探究性实验,学生往往会提出弦的材料、粗细(横截面积)和松紧程度.设计实验时要设计3组实验分别进行研究.

在探究重力大小与哪些因素有关实验时,大陆现行各版本义务教育阶段物理课本用的研究对象都是钩码,主要考虑钩码的质量已经知道无须测量(用天平测量物体质量比较耗时),用弹簧测力计测量重力可以练习使用弹簧测力计.这样的设计考虑了取材方便、操作简单、节约时间,但是有师生认为这里使用钩码是为了控制变量,控制物体的密度相同.当2013年南京市中考物理试题问“乙同学取了质量不同的苹果、小木块、小铁球各一个,并分别测出它们的质量和重力,来探究物体所受重力大小与质量的关系能否完成实验”时,很多学生就认为不可以.研究重力和质量关系时,质量是自变量,只要质量变化就可以了,至于怎么改变质量那是另外一个问题了.根据m=ρV可以知道,选质量不同的物体方法有3种:密度相同改变体积(教材的方法)、密度不同体积相同的物体、体积和密度都不同的物体.当然,要使得出的实验结论可靠程度更高,除了教材上用钩码做实验以外,还要选很多其他物体进行研究.教材只是限于版面和教学时间选取了一个特例,指导我们怎么进行研究.

有一位教师让学生提出研究影响重力大小的因素,学生猜想有物体的质量、体积和密度,教师说“质量和体积容易测量、密度不容易测量,那我们就来研究重力与体积、质量的关系吧!”很明显逻辑上是说不通的,不能因为容易测就研究,不容易测就不研究.况且,质量和体积测量出来了,密度自然就可以计算出来了.学生会发现,无法用控制变量法研究物体受到的重力与质量、体积、密度这3者之间是否有关.原因是猜想的这3个因素不是相互独立的,必须要丢下一个.

如果丢下质量,研究重力和密度、体积的关系,会得出“物体所受到的重力大小与物体的密度成正比、与物体的体积成正比”;如果丢下密度,研究重力和质量、体积的关系,会得到“物体所受到的重力大小与物体的质量成正比,与物体的体积无关”.一次得出重力大小与体积成正比(有关),一次得出重力大小与物体体积无关.根据矛盾律知道这两个结论不可能都对,根据排中律知道不可能都错(既不是有关也不是无关).要么无关,要么有关(成正比).问题出在哪里呢?

仔细研究会发现,因为m=ρV,如果物体所受的重力大小和物体的密度、体积都有关系,那一定与质量有关;如果与密度和体积都没有关系,肯定和物体的质量也无关;如果物体受到的重力大小只与密度、体积中的一个因素有关,那物体所受重力大小也和质量无关.

所以,在学生提出物体所受重力大小可能与物体的质量、体积、密度有关时,应该先放下质量这个因素,去探究重力与体积、密度的关系,发现“物体所受重力大小与物体的密度和体积都成正比”,自然也就与物体的质量成正比.

学生在提出影响浮力大小的因素的猜想时,会说出与研究对象有关的物理量:物体的体积、物体的密度、物体的质量、物体的重力.其实,这4个物理量不是相互独立的,如果直接用控制变量法是无法设计实验的.考虑到G=mg,把g当作常量,如果浮力大小与物体的质量有关,那一定与物体所受重力大小有关.同理,m=ρV,如果浮力大小与物体的体积和密度都有关系,那一定和物体的质量有关(浮力大小与物体体积和密度都没有关系,那一定与物体质量无关;浮力大小如果只和物体的密度或者物体的体积有关,浮力大小与物体的质量无关,这点难理解).此时应该先把物体的重力和物体的质量这两个量放在一边,设计两组实验分别探究浮力大小与物体的密度、物体的体积是否有关.涉及到液体的物理量,学生也可能会提出猜想:液体的体积、液体的密度、液体的质量,处理方法同前.最困扰广大师生的问题是物体浸没前,所受浮力的大小与物体浸入液体的体积是否有关?有教师根据柱形金属在浸入液体的过程中(浸没前)观察到浸入深度增加、弹簧测力计示数减小的现象,得出“浸没前,物体所受浮力大小与浸入深度有关”;也有教师认为柱体金属浸没前,随着深度的增加物体排开液体的体积也在增加,把浸入深度增加当作表象、排开液体体积增加当作本质,从而认为浮力大小与浸入深度无关;还有教师设计出图1所示中考题的实验方案来证明第二种观点.

根据前面的分析知道,在研究一个物理量与几个物理量是否有关时,提出来的猜想应该是相互独立的、同一个层次的物理量.如表5所示,我们知道,可以说物体所受浮力大小与物体排开液体的重力有关(F浮=G排);也可以说物体所受浮力大小与物体排开的液体质量有关(F浮=m排g);还可以说物体所受浮力大小与物体排开液体的体积和液体的密度有关(F浮=ρ液V排g);那对于柱形的物体浸没前,能否说物体所受浮力大小与柱体的横截面积、浸入深度和液体的密度有关呢?对于柱形物体来说,浸没前所受浮力大小可以写成F浮=ρ液Sh浸g,可以发现答案是肯定的.因此,2022年某地命制的中考物理试题从逻辑上来说是不合理的,所给答案自然也是错误的.

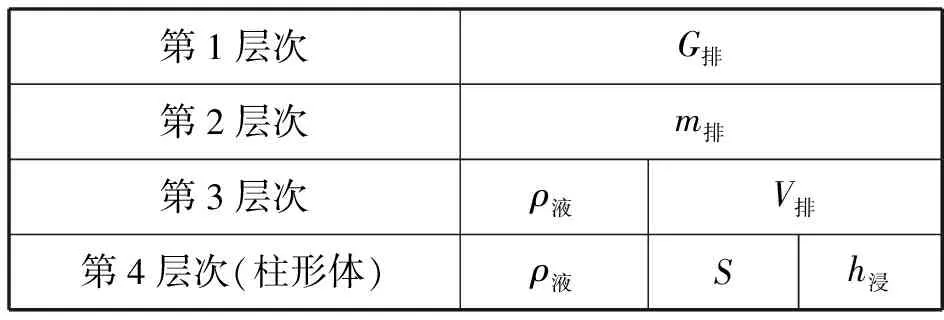
表5 影响浮力大小的因素

在研究电流大小与哪些因素有关时,要分开研究电流与电压、电流与电阻的关系.有师生根据表6的数据推理出“当导体两端电压一定时,导体中通过的电流与导体电阻成反比”的结论.

表6 研究电流与电阻关系的数据(UR=2 V)

初中学生已经学习了一次函数(含正比例函数)、反比例函数和二次函数,在I-R直角坐标系中通过这3个点的图像函数,有可能是反比例函数(I=2/R),也有可能是一个二次函数(令I=aR2+bR+c,把3组实验数据代入可以解出a、b、c的值).有教师提出,描绘I-(1/R)图像,发现是一条过(0,0)点的倾斜直线,从而说明I与1/R成正比,即I与R成反比.从数学的角度来说,这只是一种可能,也有一种可能是I与R是一个二次函数关系.要排除学生已经学过的二次函数可能,可以增加一次实验,例如15 Ω电阻.但是还有可能是一个三次函数图像,那可以做5次实验来排除这种可能……物理学家坚信,物理规律应该是遵循简单性原则的,所以,电流与电阻更有可能是反比例关系.

在研究电热与哪些因素有关时,总有学生会提出电流、电压和电阻3个猜想,有教师也很困惑,怎么把电压这个猜想排除呢?事实上,对于纯电阻电路,研究电热和任意两个物理量的关系都可以(根据控制变量的思想,这3个量不是相互独立的,必须要先“放下”一个).焦耳当年在父亲的酿酒车间发现电动机工作时发热,他就着手对电动机产生的热量进行了研究,发现与电流平方成正比、与电阻成正比.后来在研究纯电阻用电器发热时,发现用Q=I2Rt,Q=UIt,Q=U2t/R都可以,为了使得结论更简洁,当然是把两种情况进行“求同”,用一个式子Q=I2Rt统领各种情况.

4 理解方法 甄别真伪

教学中有时为了解决复杂的探究过程而采用“化繁为简”的设计方案,例如探究凸透镜成像性质与哪些因素有关这个实验,决定凸透镜成像性质的是物距和焦距之间的关系,可以说影响凸透镜成像性质的有物距和焦距两个因素.常见的处理方式有3种,一种是限定物距范围(分别是大于两倍焦距、两倍焦距和一倍焦距之间、一倍焦距以内),用同一个凸透镜分别做3次实验找规律,这种方案最简单,适合于基础薄弱的学生.第二种是限定成像性质(倒立缩小的实像、倒立放大的实像),用同一个凸透镜分别做几次实验,对数据进行分析、概括后推理、论证得出结论,这种方案适合于中等以上的学生,在分析论证中对学生的思维要求很高.第三种设计对成像性质和物距都没有限定,给一个凸透镜让学生进行自主探究.这种方案对学生思维能力要求最高,学生在完成大量实验的基础上要进行分类,归纳总结得出结论.上面每种方案用的都是焦距确定的凸透镜,但不能认为是控制变量法,我们完全可以给每组两种及以上规格的凸透镜来进行探究,但是问题就会变得复杂.之所以用焦距一定的凸透镜,是为了降低探究的难度.

“分析”表7的数据,很多学生会直接说出教师喜欢的答案:“成倒立缩小实像时,物距大于两倍焦距,像距在一倍焦距和两倍焦距之间.”事实上,根据表格中的数据,得不出成倒立缩小实像时物距大于两倍焦距(物距也大于2.5f,1.9f…).教学中,教师要引导学生如何分析数据,首先横着看,有数感的学生就会发现60比12大,再看第2行、第3行,也有这样的规律,于是可以得到“凸透镜成倒立缩小实像时,物距比像距大”(结论1).横着看(看静态)完再竖着看(看动态),会发现物距从60减小到40、30,像距从12增大到13.3、15,得出“凸透镜成倒立缩小实像时,随着物距的减小,像距在变大”,如果能同时再竖着观察像高这一列,又可以补充到“凸透镜成倒立缩小实像时,随着物距的减小,像距在变大,像也在变大”(结论2).如果还要去找规律的话,可以把表格中数据竖着相减,得到“凸透镜在成倒立缩小实像时,随着物距的减小,像距的变化量小于物距的变化量” (结论3);表格中数据横着相加,得到“凸透镜在成倒立缩小实像时,随着物距的减小,像和物之间的距离在减小”(结论3的推论);表格中数据横着相减,得到“凸透镜在成倒立缩小实像时,随着物距的减小,物距与像距的差在减小”(结论3的推论).但是,无论如何是得不出类似“成倒立缩小实像时,物距大于两倍焦距”这样结论的.那怎么办呢?

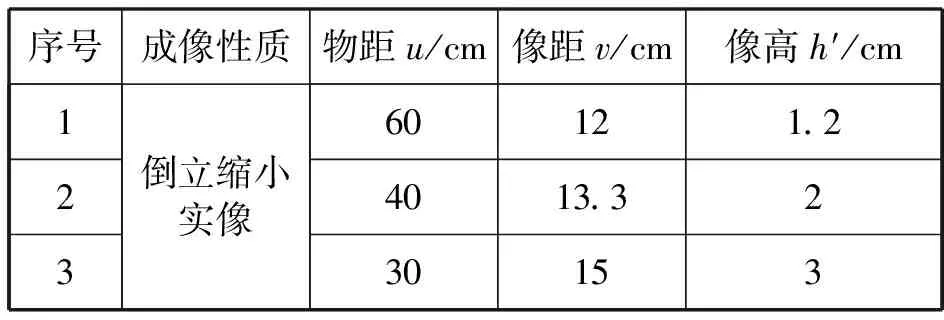
表7 凸透镜成倒立缩小实像实验数据焦距f=10 cm 物高h=6 cm

接着,去研究成倒立放大实像的情况(如表8所示),可以根据数据得出类似上面的几个结论,然后提出问题:如图7所示,凸透镜既然能成倒立缩小的实像、也能成倒立放大的实像,那有没有可能成其他性质的实像呢?如果有,像最有可能在哪两个像位置之间?物体最有可能在哪两个物体位置之间?通过几何画板去找到这样的位置,最后用焦距不同的凸透镜去验证,也可以用实验去不断试误找到成倒立等大实像时物体和像的位置.

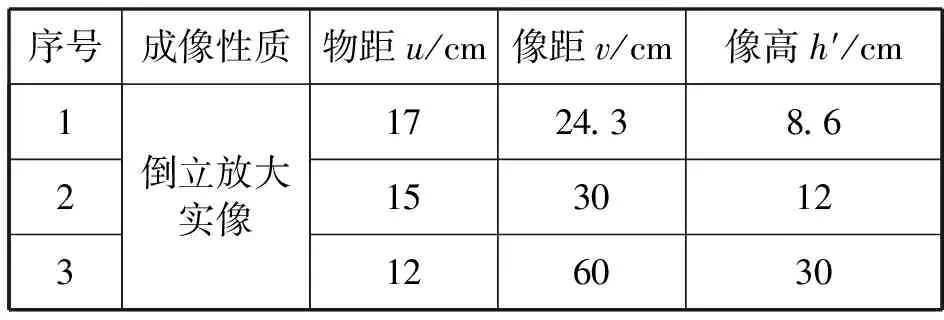
表8 凸透镜成倒立放大实像实验数据焦距f=10 cm 物高h=6 cm

图7 用磁性箭头表示物体和像

这样来探究凸透镜成实像规律才是课堂上真正应该发生的过程,也是学生思维发展并飞跃的过程.

这样就可以明显地发现,在探究凸透镜成像规律时,虽然用焦距一定的凸透镜进行实验,但不是为了控制焦距这个变量,第一种方案限定的是物距范围、第二种限定的是成像性质,这都不能叫控制变量法.

在探究杠杆平衡条件的实验中,苏科版教材的实验步骤3是“在下列情况下测量并记录动力F1、动力臂l1、阻力F2、阻力臂l2的大小.(1) 保持钩码和弹簧测力计的位置不变,改变钩码的数量;(2) 保持钩码的数量和位置不变,改变弹簧测力计的位置;(3) 保持弹簧测力计的位置和钩码的数量不变,改变钩码的位置”.有教师认为这是控制变量法,每次只改变了一个物理量,分别是阻力、动力臂和阻力臂.事实上,在第一次实验的基础上,后续实验可以改变动力臂、阻力和阻力臂中的1～3个物理量,记录动力,然后寻找这4个物理量之间的数量关系有什么共同特征.教材上每次只改变一个物理量,是为了方便实验,不能理解成只能这么做,更不能理解成是因为需要控制变量法才只能这么做.

5 学理论精髓 育优秀学生

高质量发展是全面建设社会主义现代化国家的首要任务,提高人才培养质量是高质量发展的核心目的和重点.要提高人才培养质量,必须要有一批高素质的教师队伍,教师要得到高质量发展.作为中学物理教师,在探究两个事物之间是否有因果联系时一般要用到“穆勒五法”,其中求同法要求相同点只能有一个,求异法要求不同点只能有一个,共变法要求自变量只能有一个.在探究两个物理量之间是否有因果联系设计实验时要用到控制变量法,其背后的逻辑依据是共变法.对可能的影响因素提出猜想时要保证几个不同的猜想是相互独立的,是同一个层次的物理量.不是所有的探究性实验用到的方法都是控制变量法,例如探究凸透镜成像规律和探究杠杆的平衡条件.一线物理教师要深入学习《义务教育物理课程标准(2022年版)》,把握科学思维中的科学推理和科学论证的理论精髓,要发挥逻辑知识在物理教学中的应有作用,充分发挥物理实验的综合育人功能,为党和国家培育出更多有理想、有本领、有担当的时代新人!