基于共形几何的面部模型插值构建算法

庞 敏，张 元，熊风光，焦世超，霍昕恬

(1.中北大学 计算机科学与技术学院，山西 太原 030051；2.中北大学 机器视觉与虚拟现实山西省重点实验室，山西 太原 030051；3.中北大学 计算机科学与技术学院 山西省视觉信息处理及智能机器人工程研究中心，山西 太原 030051；4.太原理工大学 信息与计算机学院，山西 太原 030023)

0 引 言

三维面部模型构建是计算机视觉、虚拟仿真领域的重要研究方向[1，2]。传统三维面部模型构建方法包括扫描建模、基于图像建模和基于三维模型重构建模。

研究者利用三维扫描设备对面部扫描得到高质量模型的方法成本高、耗时长、要求被扫描对象姿态稳定。这些特点造成该方法多适用于实验室[3]，且不易获取连续维度多表情面部模型。

基于图像的三维建模方法难以准确体现面部包含的高频信息，容易丢失褶皱、酒窝等细节[4，5]。侯守明等[6]提出三维人脸建模算法利用Kinect获取对象的色彩和深度信息，依据彩色图像建立标准面部模型，再结合深度信息对其进行拉普拉斯变形得到真实感更强的三维模型。汪淑贤等[5]提出基于图像的三维重建算法，选取同一面部不同朝向的多张图像后再根据颜色信息进行聚类、分割获取面部轮廓，基于轮廓包含的特征对面部图像立体匹配，获取带有深度的稀疏视差图进而生成面部模型的平滑点云。

基于三维变形的模型重构方法包括自由变形、骨骼变形、微分变形和基于深度学习的变形。自由变形和骨骼变形均不适用，因为他们无法为具有丰富几何细节却缺乏棱角的面部模型创建合适的约束[7，8]。基于深度学习的变形需要大量数据来支撑深度学习算法的训练，且算法适用领域也和训练数据相关，相对缺乏普适性[9]。吴越等[10]提出直接利用无三维标签的二维数据进行三维建模，通过设计弱监督损失函数使其仅根据图像进行学习；通过缩小渲染人脸与输入人脸间的差距实现三维重建。微分变形可用于具有丰富几何细节而表面缺乏棱角的模型重建，但控制点的选择会影响模型变形效果[11]。张红颖等[12]提出通过优化变形参数实现面部模型构建，改进位置映射图网络获取更准确特征，以此为基础定义初始模型参数，再融合回归方法得到参数来优化模型参数，最后优化变形模型得到最终面部模型。以上各方法都直接在三维空间实现模型构建，更容易发生畸变。

针对以上模型构建方法存在的问题，本文提出基于共形几何的模型插值构建算法通过引入共形几何三维变形降维到二维平面；提出多表情模型形状特征的插值计算来定义过渡表情建模的约束条件；提出自适应模型选择算法从不同表情的多面部模型中选择和将生成的过渡模型最接近的面部模型作为建模基础模型。本文提出的模型构建算法在保证建模效率的同时还提高了表情发生大幅度变化时模型构建的鲁棒性，相比于直接在三维空间变形建模更好避免了畸变的发生。

1 基本原理

1.1 问题描述

以现有的多个不同表情三维面部模型为基础，基于共形几何插值构建它们的过渡表情，实现表情连续维度的丰富表达。

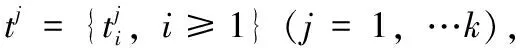
1.2 三维模型配准及特征提取

三维模型配准首先利用Super4PCS[13]算法对不同坐标系下的多个三维面部模型进行粗配准；再通过改进的ICP(iterative closest point)算法对这些三维面部模型进行精配准，将不同坐标系下的多个三维面部模型统一到同一坐标系。具体配准过程如图1所示。

图1 三维面部模型配准过程

在三维面部模型的配准过程中，首先将连续维度三维面部模型和面部模板模型依次进行主成分分析，生成累计贡献率曲线，通过对该曲线配准，获取每个面部模型和模板面部模型之间的比例因子[14]，再将二者归一化到同一尺度；之后利用Super4PCS[13]算法进行三维面部模型粗配准，在三维面部模板模型中选取同平面的4个顶点作为基点，根据交比一致性在另一三维面部模型中查找和基点对应的四点集的集合，同时求出该三维模型上每一个四点集与基点的变换矩阵；通过比较最大化公共点集，选择配准精度最高的变换矩阵进行全局变换，实现三维模型粗配准。

将经过粗配准后获取的旋转参数和平移参数作为之后基于ICP的精配准初始参数。在原始不同表情面部模型Sn中选取点pi，在原始面部模板模型Q中寻找它的最邻近点qi，过pi作点法向量ni，过qi作该点的切平面li，此时ni和li的交点为si，查找si的最邻近点，若邻近点不变还是qi，则设置|pisi|和|siqi|的边界阈值，同时剔除该阈值区域之外的所有si点，获得满足最小阈值的点对，组成集合Pn和Sn，然后再次计算变换矩阵并根据所计算的变换矩阵和集合Pn，由式(1)得到新的三维顶点集合，同时通过式(2)计算距离diskk+1，当其大于指定阈值时，继续循环执行以上步骤，直到迭代达到指定次数或disk小于指定阈值，算法停止

(1)

(2)

Rn和Tn分别是第n次迭代后获取的旋转变换矩阵和平移变换矩阵，σ为给定的收敛阈值，它的取值会影响模型配准结果的准确性，当满足distk+1<σ时，三维模型精配准算法结束。配准结果如图2所示。

图2 精配准结果

本文提出利用式(3)表示的配准精度RA来衡量精配准的准确性，配准精度是将模型配准结束时两个三维模型顶点集合的均方根误差和模型第一次配准后的两模型顶点集合均方根误差相比较来获取的。表1表示σ的取值对配准精度的影响。可以看到σ=0.001时配准精度接近于1，也就是模型配准结束时两模型顶点集合的均方根误差接近于0，即此时配准效果较好

(3)

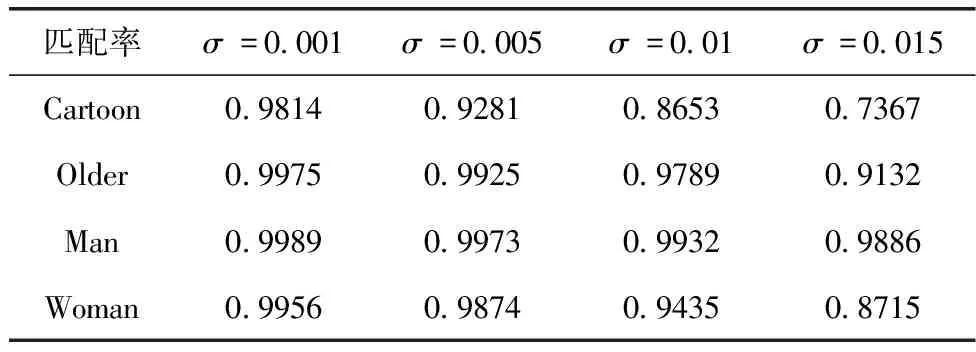
表1 σ的取值对匹配精度的影响

1.3 三维面部模型插值重构

1.3.1 面部模型3D→2D的降维处理

计算共形几何可以将几何学问题转化到工程计算领域。共形映射、准共形映射是共形几何的研究基础，在保持局部特征条件下利用解析函数将处于一种空间区域的研究对象映射到另一种空间区域。根据这一理论，共形几何为三维变形提供一种新思路，将三维空间中的变形操作降维到二维平面。

共形映射、准共形映射研究了在保持局部特征条件下如何在不同空间维度实现共形变换[15]。本文以准共形映射的局部保角性为基础研究了三维面部模型向二维平面的转换。

φ*g2=e2λg1

(4)

则此时φ是一个共形双射，两张曲面M1和M2共形等价，具有相同的共形不变量。准共形映射是对共形映射的扩展，在实际中应用更广泛，利用它实现的共形变换虽然从整体上看会存在较大畸变，但却可以保持了局部特征不变。以此为依据，本文提出了基于准共形映射的从三维空间到二维平面的降维算法。首先计算原始三维面部模型的边界，记录边界点集；其次计算模型边界线长度与角度，并将模型边界参数化到圆盘边界；最后计算模型内部顶点集合的余切拉普拉斯矩阵，并将内部顶点集合参数化到二维圆盘内部。

图3表达了三维面部模型通过准共形映射从三维空间到二维平面的降维，图3(a)是一个复杂几何属性的三维面部网格模型，图3(b)是它的降维结果。可以看到经过准共形映射降维后模型的曲率变为零，整体存在了较大畸变，但是眉眼鼻唇的局部细节特征却得到了完整的保持。

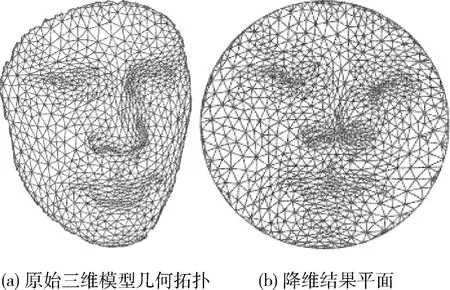
图3 三维面部模型的降维处理

1.3.2 插值计算过渡模型特征点

(5)

式中：j代表通过式(5)生成的表情过渡模型索引值，i代表模型中特征点索引值，α代表每个面部模具有的权值，定义了包括模板模型和不同表情连续维度面部模型在内的所有原始模型对将生成的过渡模型的影响，α的定义如式(6)

(6)

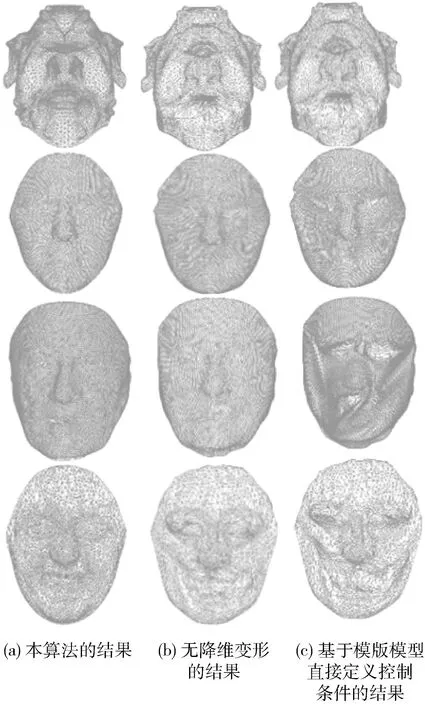
(k-1) 为除模板模型外原始模型数量，di索引值为i的原始模型与模板模型对应特征点中最大距离差。dm为生成的表情过渡模型与面部模板模型的距离，0

1.3.3 自适应定义基础模型

(7)

1.3.4 面部模型构建

利用式(5)获取的特征点集合Tj为控制点，引导利用式(7)定义的基础模型的二维平面准共形迭代，获取具有过渡表情的面部模型的二维平面数据，具体算法如下：

步骤1 从基础模型的特征点集合t中选取控制点，利用特征点集合Tj中与选取的控制点对应的顶点，通过式(8)、式(9)计算处理，得到集合t和Tj所包含的对应顶点之间的初始变换关系f0和v0

(8)

v0=μ(f0)

(9)

其中，μ为贝尔特拉米系数[17]；Fb为线性贝尔特拉米求解器[17]。

步骤2 利用基础模型的网格结构顶点信息vn，通过式(10)～式(12)分别计算μn+1、fn+1和vn+1

(10)

(11)

(12)

其中，A为拉普拉斯平均算子，δ为参数化到二维平面顶点坐标构成的矩阵。

图4显示了准共形迭代处理结果，其中图4(a)是面部模型降维得到的二维平面，图4(b)是对二维平面准共形迭代的处理结果。

图4 准共形迭代的运行结果

将准共形迭代得到的二维模型的拓扑信息和部分顶点的几何信息为依据，实现模型从二维平面到三维空间的转换。

首先根据二维模型拓扑信息和几何信息计算模型的余切拉普拉斯矩阵；然后以一部分顶点为依据定义约束条件；最后引入最小二乘法构建尽可能满足约束条件的三维模型顶点信息，得到具有过渡表情的三维面部模型。具体算法如下：

步骤1 根据式(13)计算模型的余切拉普拉斯矩阵

(13)

其中，在二维平面中边 (xi，xj) 会与其它顶点构成三角形，αij和αji是该三角形中与边 (xi，xj) 相对的角的度数。当 (xi，xj) 为二维平面内部边时，可以和两个顶点分别构成两个三角形，此时就出现两个 (xi，xj) 边的对应角，度数分别为αij和αji；而当 (xi，xj) 是边界边时，则只能和一个顶点构成三角形，只有一个对应角度数为αij。

步骤2 将三维空间的x、y、z坐标结合余切拉普拉斯矩阵构建线性系统：Wx=0，Wy=0，Wz=0。

步骤3 从非特征点所在区域选择m个顶点保存到集合C中，C={s1，s2，s3，s4，…sm}，每个顶点为Vs=(xs，ys，zs)，s∈C，将这m个顶点和步骤2构造的线性方程相结合，构建长度为 (n+m)×n的系统，如式(14)～式(19)所示。其中A的计算由式(15)、式(16)所示

Ax=bx

Ay=by

Az=bz

(14)

(15)

(16)

(17)

(18)

(19)

步骤4 利用最小二乘法求解满足如式(20)线性方程的最小值，得到x=(ATA)-1ATbx，y=(ATA)-1ATby，z=(ATA)-1ATbz，则最终所求的顶点坐标为Vnew=(x，y，z)

(20)

图5显示了模型在不同空间的转换效果，图5(a)表示了二维平面模型，图5(b)表示了利用本方法空间转换得到的三维面部模型。

图5 2D→3D模型转换算法

2 分析与讨论

本文以Matlab为开发工具，以美国纽约州立大学宾汉姆顿分校的BU3DFER三维人脸数据集作为数据源，验证了所提出的利用插值构建面部模型算法的准确性。

2.1 算法运行效果

图6中第一行是原始模型，包括图6(a)模板模型和连续维度的不同表情模型。本实验选择眼睛和嘴巴部分的特征点定义约束条件，插值生成不同表情的过渡模型。图6第二行显示了各原始模型中选取的特征点。图7显示了本文算法的插值重构结果，其中图7(a)显示的是原始模型中满足差值最小条件的表情模型被降维得到的二维平面，以及在该平面上定义的约束条件，其中圆圈代表来自原始表情模型特征的控制点起始位置，方框代表来自插值后特征点目标位置。其中图7(b)利用约束条件引导二维模型准共形迭代获取的结果模型，图7(c)显示了通过三维模型恢复算法将图7(b)表示的模型从二维平面转换到三维空间，得到的具有过渡表情的三维面部模型。

图6 原始模型

图7 重构结果模型

图8给出了将本文提出的算法应用于不同性别、年龄的面部模型的实验效果，其中图8(a)列表示面部模板模型，图8(b)列和图8(c)列表示连续维度的不同表情面部模型，图8(d)列和图8(e)列是从不同角度展示了利用本算法生成的过渡模型。可以看到图8(a)～图8(c)列的眼睛和嘴巴包含了闭合和打开状态，图8(d)、图8(e)显示的结果模型则在保持眼睛和嘴巴等面部局部细节特征同时面部表情又发生一定变化。

图8 本文算法的模型插值结果

2.2 传统模型构建算法效果对比

构建面部这类细节丰富而没有明显棱角特征的三维模型时，基于FFD变形或基于骨架变形的重构方法都不适用，所以研究者多选择使用基于微分变形的重构方法来处理此类模型。表2将本文提出的算法和基于拉普拉斯算子的面部模型重构算法及基于微分坐标的面部模型重构算法的性能进行比较，包括定义约束条件时需要的控制点个数和算法运行时间。可以看到本文算法是在二维空间实现模型变化，所以相较于三维空间的变形，需要的控制点更少，且算法运行时间更短。图9显示了3种算法的运行结果，其中图9(b)是本文算法结果模型，图9(c)是基于拉普拉斯算子的面部模型重构算法的结果模型，图9(d)是基于微分坐标的面部模型重构算法的结果模型，可以看出利用他们提出的模型重建算法，直接在三维空间发生形变实现三维模型重建的算法时，对于特征丰富、形变较大的区域，如唇眼部分很容易发生畸变。而本文提出的算法，由于模型变化在二维实现，此时不需要处理深度信息，使重构结果在保持细节的同时产生更少的畸变。

表2 本算法和其它算法的性能比较

图9 不同模型重构算法处理结果比较

2.3 消融实验

为了验证该模型构建算法中共形几何部分和插值构建部分的重要性，将在BU3DFER数据集上进行过渡表情模型构建的消融实验。消融实验根据本文提出算法中包含的重要设计分为以下3个部分：

(1)本文方法：构建了包含本文提出的基于共形几何的模型降维处理及基于多模型形状特征插值生成的模型构建约束条件的完整过渡表情模型构建算法。

(2)对变形算法进行替换，将基于共形几何的降维变形替换成直接在三维空间进行的微分变形，不再对三维模型进行降维处理，其它结构不变。

(3)对变形基础模型和变形约束条件进行替换，将利用多模型特征点插值得到的控制约束条件和根据特征点自适应选择的基础模型替换为以根据模板模型到某个表情模型特征点距离定义约束条件、以模板模型为基础模型，其它结构不变。

消融实验构建过渡表情的面部模型结果如图10所示。图10(a)是本文方法得到的建模结果，图10(b)是将基于共形几何模型构建方法替换为微分变形的建模结果，图10(c)是将本文的控制约束条件的定义及自适应选择基础模型替换为按单一特征点距离构建约束条件及使用模版模型作为基础模型的建模结果。相比于图10(a)本文算法的建模结果，图10(b)中模型的较大变化区域会出现扭曲，如第一行模型的鼻子、嘴巴和第二行模型的眼睛；而图10(c)中模型在较大的变形区域内也会出现明显的畸变，如第三行模型的嘴巴和眼睛出现明显的扭曲。

图10 消融算法的定性结果

可以看到，本文提出的模型构建方法的效果是更好的，验证了共形几何模块和插值定义特征点及自适应选择基础模型模块在构建过渡表情面部模型时的重要性，它们都提高了模型变形重构的运行效果。

3 结束语

综上所述，本文在对模型配准的基础上通过准共形映射将其降维到二维平面，解决了现有建模方法不易在三维空间构建连续维度多表情模型的问题；然后基于多面部模型特征点插值生成过渡模型特征点并构造控制约束条件；同时根据插值生成的特征点选择和其距离最小的表情模型，自适应定义变形基础模型；最后利用控制约束条件引导基础模型准共形迭代，生成具有过渡表情的面部模型。实验验证了本文提出的算法在保持面部模型局部特征的同时很好实现了连续维度多表情模型的构建。在今后的工作中，将进一步研究连续维度不同表情中如果出现大幅度变化表情时配准效果欠佳的问题，并考虑在获取面部模型特征点时引入深度学习算法，得到更合理的特征点引导面部模型重构。