基于三支特征表示的抽象画情感聚类分析

赵婧琦，李宇蕊，杜明晶+，刘静玮

(1.江苏师范大学 美术学院，江苏 徐州 221100；2.江苏师范大学 计算机科学与技术学院，江苏 徐州 221100；3.中国航天科工集团第二研究院 七〇六所，北京 100854)

0 引 言

长久以来，针对绘画作品情感分析的研究备受关注。随着计算机视觉技术的日益成熟，研究人员开始运用计算机进行大规模的绘画情感分析[1]。

相对于具象画，抽象画采用的是无逻辑的创作风格和非具象的表现手法[2]。由于缺少具体物象的描述，因此其较难与特定的情感建立直观联系。这使得抽象画的情感分析变得非常困难和复杂。该问题引起了诸多学者的关注，涌现了诸多采用监督学习方法的抽象画情感分析的研究。监督学习表现取决于数据集规模和标注质量，但人工标注耗时且易受主观影响。因此，无监督学习在抽象画情感分析中具有极大的应用前景。

针对抽象画的情感分析问题，本文提出了一种基于三支特征表示的多核聚类方法(multiple kernel K-means using three-way features，MKKM-3WF)。首先采用本文提出的基于三支决策的颜色特征表示方法和纹理特征表示方法以及改进的深度学习模型，分别提取抽象画的颜色特征、纹理特征和高层语义特征；然后使用核函数构建不同特征的相似度矩阵；最后采用多核聚类算法完成多特征融合与图像的情感划分。

1 相关工作

1.1 抽象画情感分析

本节主要探讨抽象画图像情感分析领域的研究进展。该领域的早期研究深受自然语言处理工作的启发。例如，Yanulevskaya等[3]将文本处理中的词袋模型引入到抽象画图像处理中，提出了一套视觉词袋表征框架，并运用支持向量机分类模型实现情感预测。Sartori等[4]将该算法运用到了业余抽象画的情感分析中，也取得了良好的预测结果。在图像情感分析中，纹理特征也扮演着至关重要的角色。文献[5]通过所设计的特征滤波器提取这些灰度图像的纹理特征，在此基础上采用支持向量机进行情感分类。深度学习技术的出现给抽象画情感分析注入新的动力。文献[6]除了利用人工特征表示方式提取抽象画图像底层颜色、纹理特征外，还运用卷积神经网络提取图像的高层语义特征。白茹意等[7]在卷积神经网络的基础上引入迁移学习的思想，提取抽象画图像的高层语义信息。杨子文等[8]针对抽象画图像标注困难、标注较少的问题，提出了两层迁移学习卷积神经网络设计方案。上述抽象画图像情感分析工作均采用监督学习策略，而应用无监督学习方法的工作尚未得到广泛关注。

1.2 三支决策

为解决现实世界中的不确定信息决策问题，Yao[9]提出了三支决策(three-way decisions，3WD)理论。近年来，学者们将三支决策进行了拓展，构建了诸多理论模型，如三支属性约简[10]、三支分类[11，12]、三支聚类[13，14]和三支冲突分析[15]等。针对混合型数据，胡声丹等[16]将三支决策和主动学习思想引入标签传播算法中，提出了三支标签传播的半监督属性约简方法。Du等[17]结合序贯三支决策的思想，提出多步三支聚类方法。为解决q环正交模糊信息中的冲突问题，Li等[18]提出基于三支决策和粗糙集理论的三支冲突分析和解决模型。三支决策理论在处理复杂动态的不确定性问题方面得到了广泛应用。该理论在信用评价[19]、文本分析[20]和推荐系统[21]等领域发挥着重要作用。但是，当前鲜有应用于图像特征表示的相关工作。

2 基于多核的情感聚类

2.1 基于三支决策的颜色特征

本文选择使用HSL颜色空间，该颜色空间基于人类对颜色的感知能力，更适用于图像的情感分析工作。此外，相比于其它类似的颜色空间，如HSV颜色空间和L*a*b*颜色空间，HSL颜色空间在后续划分操作中更具优势。

HSL颜色空间将颜色分为3个分量：色调(Hue)、饱和度(Saturation)和明度(Lightness)。色调通过角度来表示，范围为0°到360°。从0°的红色开始，逆时针旋转，经过120°的绿色和240°的蓝色，然后回到360°的红色。圆柱的直径方向表示饱和度，圆柱轴心的饱和度为0，表示最低饱和度；圆柱边缘的饱和度为1，表示最高饱和度。圆柱的垂直方向表示明度，圆柱顶部的明度为1，呈现白色；圆柱底部的明度为0，呈现黑色；圆柱中间部分的明度为0.5，表示中等明度，对应HSV中亮度V等于1的情况。

传统的颜色量化方式采用的是硬化分的方式，将某个区间指定为某种颜色，即颜色量化采用二支划分的方式(属于或者不属于)。这种划分方式将导致非此即彼的问题，而人类对颜色的视觉感知具有模糊特性，因此会产生与人们视觉感知的偏差。本文采用三支决策理论来解决该问题。

下文将介绍本文提出的三支决策方案。首先，从HSL颜色空间中提取出3类不包含色彩信息的颜色，它们分别是白色、黑色和灰色。白色的范围是明度L>0.95；黑色的范围是明度L<0.05；灰色为明度处于0.05≤L≤0.95且饱和度S<0.1。

接下来，将针对剩余的颜色空间开展三支划分。在H通道上，我们将依据人类对颜色的感知将色调设定为10个子集，并将它们命名为红、橙、黄、绿、青、天蓝、蓝、紫、洋红、玫红。在S通道上，我们将饱和度设定为2个子集：不饱和与饱和。在L通道上，我们将明度设定为3个子集：暗、中、明。

(1)

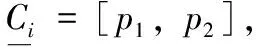
(2)

通过笛卡尔积，可以将3个通道上的子集组合成60个HSV颜色空间的子集，再加上3种不含色彩的颜色子集(白色、黑色和灰色)，共63个颜色特征。

2.2 基于三支决策的纹理特征

本文提出一种基于三支决策的纹理特征表示方法可以有效地获取抽象画中的纹理信息。

首先，将抽象画图像转换为灰度图像，该灰度图像表示为矩阵G。

接着定义4种滤波矩阵形式，分别是近似(低通)矩阵、细节(高通)矩阵、伴随近似(伴随低通)矩阵和伴随细节(伴随高通)矩阵。

近似矩阵A中各元素的定义如下[22]

(3)

式中：下标 (i，j) 被用来标识矩阵A的i行第j列的元素。

细节矩阵D中各元素的定义如下[22]

(4)

伴随近似矩阵A†中各元素的定义如下[22]

(5)

伴随细节矩阵D†中各元素的定义如下[22]

(6)

接下来，对灰度图像矩阵进行二级小波变换，提取图像水平、垂直和对角方向的信息。一级小波分解得到的低频子图的计算公式如下[22]

G′2n×2m=A†2n×4n·G4n×4m·A4m×2m

(7)

式中：下标2n×2m表示矩阵G′是一个2n行2m列的矩阵。其它矩阵的下标也采用这种表示方法标识矩阵的大小。

在子图G′2n×2m的基础上进行二级小波分解，所得水平、垂直和对角方向的子图分别表示为TH、TV和TD，它们的计算公式如下[22]

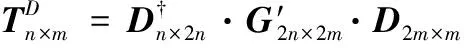
(8)

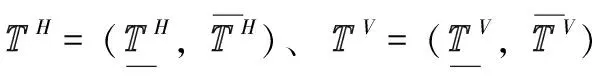
类似于颜色特征的计算，纹理特征上的三支量化计算公式为

(9)

式中：[p1，p2]为纹理特征子集Ti的最小区间，[b1，b2]为其最大区间。

通过笛卡尔积，可以将3个方向的信息子集组合成8个纹理特征。

2.3 高层语义特征

本文提出VGG16的改进模型，用于提取抽象画图像中的高层语义特征。

为去除特征中无用信息和噪声，在VGG16的输出层之前增加一层包含10个神经元的全连接层。本研究在原VGG16最后一个全连接层(包含4096个神经元)和新增的全连接层(包含10个神经元)之间，增加了两个全连接层。这样做是为了让网络结构更稳定，并且增强模型的非线性变换能力和表达能力。两个额外添加的全连接层的神经元个数分别为1024和256。本文最终目标是提取最后一层全连接层(包含10个神经元)上的权重，这样的低维特征有助于提升后续处理步骤的效率和聚类精度。

2.4 多核k均值聚类

本文采用多核k均值算法(multiple kernel K-means，MKKM)[23]实现图像的聚类。

在多核学习中，X={x1，x2，…，xn} 表示一个包含n个样本的数据集。φp(·) 表示第p个特征映射函数，这类函数可以将数据从原始空间映射到新的特征空间。因此，数据x在m个特征函数的融合表达形式为φβ(x)=[β1φ1(x)T，…，βmφm(x)T]T，其中β=[β1，…，βm]T为m个特征函数的权重向量。因此，融合后的核函数形式如下所示[24]

(10)

式中：Kp(·，·) 为第p个特征映射函数φp(·) 所对应的核函数形式。

可以用上述核函数形式，把原始数据集表征转换成核矩阵形式Kβ[24]

(11)

式中：Kp是第p个核函数所转换的数据核矩阵。

在上述定义的基础上，MKKM的目标函数可以定义为如下形式[25]

(12)

式中：H是一个聚类划分矩阵，大小为n×k，其中n是样本数目，k是聚类数目；In和Ik分别表示大小为n×n和k×k的单位矩阵；βp为权重向量β的第p个分量。

可以通过一种两步迭代优化算法来自适应地更新权重β并求解式(12)的目标函数[26]。

(1)固定β，更新H。该种情况下，式(12)与下式等价[27]

(13)

可以通过特征分解进行求解，H的最优解为Kβ最大的前k个特征值所对应的特征向量。

(2)固定H，更新β。该种情况下，式(12)与下式等价[27]

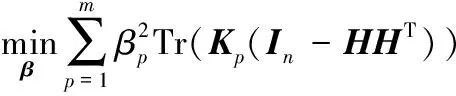
(14)

可以将上述问题看作带有线性约束条件的二次规划问题，进而求解相应的β。

2.5 基于特征融合的聚类情感分析

基于特征融合的聚类情感分析框架如图1所示。

图1 本文方法框架

首先对抽象画图像进行预处理：将不同规格的图像缩放为统一大小；将部分灰度图像转换到RGB空间中。

第一个核心阶段是使用2.1节～2.3节描述的方法分别提取抽象画图像的颜色特征、纹理特征以及高层语义特征。

本文选用高斯核函数作为特征映射函数。高斯核函数是多核学习中最常用的核函数之一，其形式如下

(15)

式中：σ为高斯核函数的带宽参数，控制着高斯函数的宽度。本文将该参数设置为1。

令K1、K2、K3分别表示使用高斯核函数对抽象画图像的颜色特征、纹理特征和高层语义特征计算得到的核矩阵。可以使用加权平均的方式得到初始融合核矩阵，其形式如下

(16)

第二个核心阶段是使用2.4节描述的MKKM聚类算法实现抽象画图像情感划分。

3 实验部分

3.1 数据集

本文选用广泛应用于抽象画情感分析领域的MART数据集和DeviantArt数据集[3，4]。MART数据集共包含500张专业的抽象画作。DeviantArt数据集共包含500张业余爱好者绘制的抽象画作。

3.2 基准算法

为了验证所提方法的有效性，本文选择了几种性能优异的聚类方法作为基准。

PCA+k-means[28]：对原始图像采用主成分分析(principal component analysis，PCA)进行降维，在降维后的特征上进行k-means聚类。本文将此种策略记作PCA+k-means。

UMAP+k-means[29]：对原始图像采用统一流形逼近与投影方法(uniform manifold approximation and projection，UMAP)[30]进行降维，在降维后的特征上进行k-means聚类。本文将此种策略记作UMAP+k-means。

AE+k-means[31]：采用自动编码器(AutoEncoder，AE)[32]对图像进行特征提取，在提取的特征上进行k-means聚类。本文将此种策略记作AE+k-means。

DCEC[33]：一种经典的深度卷积嵌入聚类模型，该模型直接可以读入图像数据并给出聚类结果。本文将此种策略记作DCEC。

3.3 评价标准

为衡量聚类结果的好坏，本文采用3种常用的聚类评价指标：准确度(accuracy，ACC)、Fowlkes-Mallows指数(Fowlkes-Mallows index，FMI)和归一化互信息(norma-lized mutual information，NMI)。

3.4 对比实验

将本文的方法与4种基准聚类方法进行对比，表1展示了这些方法在MART和DeviantArt数据集上的聚类效果。从表1中可以看出，本文方法在ACC、FMI和NMI这3类指标上都显著优于其它4种基准方法。在MART数据集上，本文方法的ACC指标达到了0.872，而4种方法的ACC值均低于0.7；本文方法的FMI值为0.807，其相较于4种基准方法平均提高了20个百分点；在NMI指标上，本文方法得分为0.46，超过4种基准方法一个数量级以上。而DeviantArt数据集上，本文方法的ACC指标达到了0.884，而4种方法的ACC值均低于0.6；本文方法的FMI值为0.819，其相较于4种基准方法提高了26个百分点以上；在NMI指标上，本文方法得分为0.543，同样超过4种基准方法一个数量级以上。

表1 方法性能

综上所述，该方法明显优于其它基准方法，包括两种基于深度学习的基准方法(AE+k-means和DCEC)。这充分说明在处理抽象画图像的情感分析问题时，采用多特征融合的聚类策略具有更为明显的优势。3种不同特征(颜色特征、纹理特征和高层语义特征)能够捕捉抽象画的不同方面或视角。多核聚类算法有助于发现这些特征之间的一致性和差异性，通过整合3种特征，实现信息的互补和校正，从而提供更全面、更准确的情感表征，最终达到更高的聚类精度。

3.5 消融实验

本节通过消融实验验证本文提出的颜色特征表示方法和纹理特征表示方法的有效性。将本算法中基于三支决策的颜色特征分别替换为Itten颜色特征[34]和颜色命名特征[35]，并分别记作MKKM-Itten和MKKM-Name。将本算法中基于三支决策的纹理特征分别替换为GLCM纹理统计特征[36]和Tamura纹理特征[37]，并分别记作MKKM-GLCM和MKKM-Tamura。此外，还同时替换掉了颜色特征和纹理特征。将本算法使用颜色特征和纹理特征同时替换Itten颜色特征[34]和GLCM纹理统计特征[36]，将此种模型记作MKKM-IG。将本算法使用颜色特征和纹理特征同时替换颜色命名特征[35]和Tamura纹理特征[37]，将此种模型记作MKKM-NT。

表2展示了消融实验的结果。从表中的聚类结果可以看出，本方案的聚类表现明显优于改动方案。相较于基于颜色特征的改动方案(MKKM-Itten和MKKM-Name)，本方案在ACC、FMI和NMI上的平均提升分别为31个、24个和49个百分点。相较于基于纹理特征的改动方案(MKKM-GLCM和MKKM-Tamura)，本方案在ACC、FMI和NMI上的平均提升分别为15个、15个和26个百分点。相较于颜色和纹理特征同时改动的方案(MKKM-IG和MKKM-NT)，本方案在ACC、FMI和NMI上的平均提升分别为36个、26个和50个百分点。基于三支决策的颜色特征相较于两种经典的颜色特征(Itten颜色特征和颜色命名特征)，在应对抽象画情感聚类任务时具有明显优势。同样地，基于三支决策的纹理特征相比于两种经典的纹理特征(GLCM纹理统计特征和Tamura纹理特征)，也有较大提升。同时融合三支决策的颜色特征和纹理特征的方案相较于同时融合经典颜色特征和纹理特征的方案具有非常显著提升，且优于仅改动一种特征的方案。这可能源于三支决策在不确定处理方面具有天然优势。

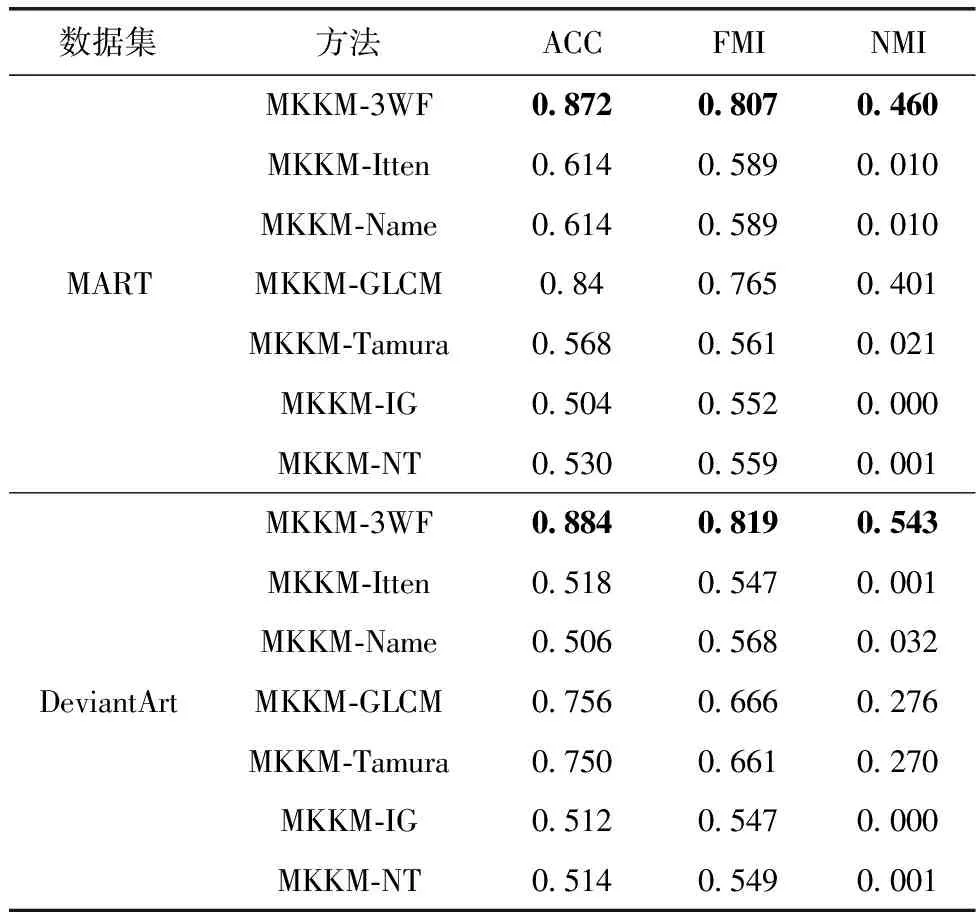
表2 消融结果

综上所述，本文提出的两种图像特征表示方式显著提高了抽象画的情感聚类分析表现。

4 结束语

本文提出了一种抽象画图像自动情感聚类方法。所提出的基于三支决策的颜色特征表示方法和纹理特征表示方法以及改进的深度学习模型能够有效地提取抽象画中的颜色特征、纹理特征和高层语义特征。多核k均值算法能够自适应地融合从抽象画图像中提取的3种特征，并实现情感聚类分析。实验结果表明，相较于4种基准方法，本文方法取得了更好的聚类表现。多模态环境下的情感聚类分析是未来的研究方向。