基于标签挖掘的个性化推荐算法

时光洋，于万钧，陈 颖

(上海应用技术大学 计算科学与信息工程学院，上海 201418)

0 引 言

推荐算法的价值在于帮助用户解决信息过载问题，做出更好选择。现有的推荐算法一部分主要有，深度矩阵分解算法[1]、强化学习推荐算法[2]、用户记忆网络顺序推荐[3]。它们的特点是加强了对隐含特征的学习，通过神经网络模型训练来提升推荐效果，但对于存在的显式特征没有充分挖掘出价值。例如，用户使用的标签信息和用户评分[4]。对此，有部分研究人员是关注标签信息的挖掘，Lin等[5]利用层次结构分析标签之间的关联特征，但没有考虑到用户自身对于不同标签的喜好程度大小。Zhu等[6]对标签推荐列表长度进行了优化，考虑了列表中标签的相关性，却忽略了不同标签所占的权重。Dai等[7]从评论中提取出特征及其情感程度，构建用户商品的特征权重，在计算方式中没有考虑到用户使用标签的显式作用对于用户商品特征权重的影响。

为解决上述问题，本文从用户对标签兴趣和用户对标签的评分信息两个方面展开研究，提升对用户兴趣挖掘的准确性。主要工作在以下几个方面：

(1)对用户所使用的标签进行操作，通过自定义函数确定用户对标签偏好值：分别计算用户对标签喜好值和用户对标签依赖度，将两者进行乘积运算得到用户标签偏好值。

(2)将用户对物品评分迁移为用户对所使用的标签评分，以此来计算标签在同一用户所使用的所有标签中所占权重。当其它用户使用相同标签时，则用户间相似度高。

(3)将标签偏好值与标签权重进行线性组合，从而计算出用户最终的标签兴趣度。引入矩阵分解算法，对评分进行预测。

实验结果表明，相比于其它评分预测算法，本文算法模型预测精准度有所提高，取得较好效果。

1 相关工作

1.1 计算标签相似度方法

Jaccard标签相似度、皮尔逊系数标签相似度和TF-IDF标签相似度是主要计算标签相似度的推荐方法。基于Jaccard标签相似度主要是利用集合操作来处理标签，不同标签所占权重缺乏考虑，导致推荐精度较低。皮尔逊相关系数计算标签相似度是将用户所打标签看作变量，计算它们之间的皮尔逊相关系数，但皮尔逊相关系数假设数据是正态分布的，如果数据未能满足这个假设，计算结果可能会失效。TF-IDF标签相似度计算根据标签使用次数，忽略了评分信息因素。

1.1.1 Jaccard标签相似度

Jaccard相似系数定义请参见文献[8]，计算公式如下[8]

(1)

1.1.2 皮尔逊相关系数标签相似度计算方法

皮尔逊相关系数是用于度量两个变量X和Y之间的相关性，其值介于-1与1之间。相关系数的绝对值越大，相关性越强，反之相反。皮尔逊相关系数计算公式如下[9]

(2)

1.1.3 TF-IDF标签相似度计算方法

令标签集合T={t1，t2，…，td}，d为标签数量。wi表示给物品i打上标签ti的用户数量。每个标签ti对应权重为wi，全部标签对应的权重集合为W={w1，w2，…，wd}。对标签集T进行统计，得出所有标签被用户使用次数的集合D，D={d1，d2，…，dd}，其中dj表示标签ti被用户使用次数。TF-IDF计算步骤分为以下几步[10]：

步骤1 计算标签词频(TF)，即每个标签i在每个物品使用次数。计算公式如下所示

(3)

步骤2 为计算标签的逆文档频率(IDF)，用以表示标签的常见度，利用以下公式进行计算

(4)

步骤3 合成IF-IDF公式，计算公式如下

TF-IDF=TFi*IDFi

(5)

1.2 矩阵分解模型

1.2.1 隐语义模型

隐语义模型(latent factor model，LFM)是推荐系统领域一个热门研究问题，核心思想是通过隐含特征关联用户兴趣和物品，通过矩阵分解对用户-物品评分矩阵R进行分解，分解成用户-特征矩阵P和物品-特征矩阵Q[11]。其结构如图1所示。

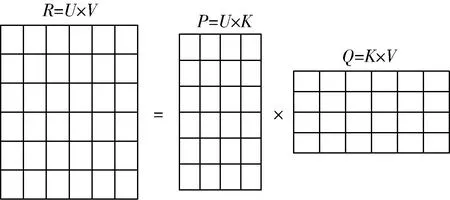
图1 矩阵分解模型

其中，K表示特征个数。

令pj和qk分别代表用户潜在特征向量和物品潜在特征向量，评分预测计算公式如下

(6)

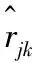
(7)

式中：μ表示用户评分均值，bj表示用户偏置项，bk表示物品偏置项。

1.2.2 隐式反馈SVD++模型

LFM和带有偏置项隐语义模型(BiasSVD)都过度依赖用户-物品评分矩阵，BiasSVD模型中虽然加入评分平均分μ、用户偏置项bj和物品偏置项bk，却没有考虑显示用户历史行为对用户评分预测的影响。在SVD++模型中，考虑了用户对其所有有过评分行为的物品的隐式反馈[12]。所以隐式反馈SVD++模型的预测表达式为

(8)

式中：Nk表示物品ik受到用户的评分集合，xv表示用户uv的特征向量。

根据上文描述，本文主要是在现有理论TF-IDF算法和SVD++模型基础上，将用户对标签的依赖度和用户标签兴趣相似度的概念结合起来，并将其引入到SVD++模型中。这样做可以提升模型的推荐效果。具体而言，利用TF-IDF算法计算每一个用户对标签的依赖度，即某个用户对某个标签感兴趣的程度。通过这种方式，可以更加准确地描述用户的兴趣特点，从而提高推荐系统的推荐质量。另一方面，在传统的SVD++模型中，主要考虑了用户对物品的评分数据，并未考虑用户兴趣的细节。为了更准确地描述用户的兴趣特点，本文引入了用户标签兴趣相似度的概念，通过标签来反映用户之间的相似度。通过这种方式，将用户对于标签兴趣引入到SVD++模型中，从而更好地体现用户的个性化需求和偏好。综上所述，本文通过引入TF-IDF算法计算用户对标签的依赖度以及用户标签兴趣相似度的概念，对传统的SVD++模型进行了改进，以提高推荐系统的性能和准确性。

2 用户标签兴趣度和标签权重

2.1 建立用户-资源评分矩阵

令用户集合为U={u1，u2，…，um}，物品集合为V={v1，v2，…，vn}，且|U|=m，|V|=n。建立用户-物品评分矩阵为R，R=[rij]m×n是一个m×n的用户-物品评分矩阵，rij表示用户ui对物品vj的评分，其中i=1，2，…，m，j=1，2，…，n。对于物品的评分完全是根据用户是否愿意给物品打分或用户是否与物品发生过交互，用户没有与物品产生过交互或者用户不愿给物品打分，那么用户u对于物品v的评分不存在，则rij=0。在实际推荐中，用户与物品发生交互的次数远少于物品本身数量，并且存在发生交互没有打分情况。在两种因素下，用户-物品评分矩阵R通常是一个稀疏的矩阵。矩阵R如下

(9)

令标签集合为T={t1，t2，…，td}，且|T|=d。将用户对物品的评分看作为用户对物品及其相关标签的评分，并构建用户-标签评分矩阵P，puitj代表用户ui对于标签tj的评分，其中m=1，2，…，m，t=1，2，…，d。矩阵P如下

(10)

根据用户-标签评分矩阵P，构建用户-标签交互矩阵Z=[zut]m×d，zuitj代表用户ui是否与标签tj发生交互，当put≠0时，zut=1即用户u与标签t发生交互，反之zut=0则未发生交互。zut计算公式为

(11)

2.2 用户对标签偏好值

标签是用户描述、整理、分享网络内容的一种新的形式，也是反映用户自身的兴趣和态度。用户对于标签的喜好可以使用二元关系表示，如“喜欢”或“不喜欢”；也可以使用“连续数值”表示喜好程度。二元方法表示虽然简单明了，但是描述精度不够，对标签进行喜好程度大小排序时，无法区分标签之间的差异。所以，这里采用“连续数值”来表达用户对于标签的偏好值。

计算用户对标签喜好值，相同标签用户可能会用来标记不同物品，不同的标签也会标记相同的物品。因此，用户对标签的喜好值计算公式如下，其中u∈U，t∈T

(12)

假设用户评分次数较少，通过上面计算方法可能使得计算结果存在较大误差，利用TF-IDF算法计算用户对标签的依赖程度。首先，计算TF-IDF算法中TF部分，即标签使用频率，计算公式如下

(13)

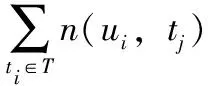
目前，社交标签的使用已经成为一种普遍现象，导致互联网中存在“马太效应[13]”，即随着热门标签的展示次数增多，它们变得越来越受欢迎，冷门标签随着使用次数较少变得越来越冷门。事实上，冷门标签的使用能够更好体现出用户的个性和特点，为了消除马太效应的影响，更加准确的挖掘用户偏好，本文利用TF-IDF算法中IDF部分，对热门标签进行数值惩罚。公式如下

(14)

综合上述，用户对标签依赖度数值计算公式为

TF-IDF(u，t)=TF(u，t)×IDF(u，t)

(15)

综合考虑，用户对于标签的主观喜好值和利用TF-IDF算法计算用户对于标签的依赖度数值，可以得到用户对于标签的偏好值为

Pre(u，t)=Deg(u，t)×TF-IDF(u，t)

(16)

2.3 标签权重值

在用户对物品进行评分时，通常情况下会同时给物品打上自己喜欢的标签，这些标签代表了用户对物品的主观评价[14]。例如，当用户观看了一部动漫电影并且非常喜欢，为了表达他们的喜爱，用户可能给这部电影评分为5分，并添加“cartoon”这个标签。这个标签在用户打过的所有标签中的权重会更大，如果其它用户也使用了这个标签来标记自己看过的物品，那么可以认为这些用户之间的相似度较高。

通过利用物品评分来计算标签权重，计算公式如下

(17)

2.4 用户标签兴趣度

用户对标签的兴趣度表示了用户对该标签的兴趣程度的大小，若用户对于某个标签的兴趣度较大，则类似标签或该标签标注的其它物品可以向用户推荐。计算用户对标签的兴趣程度，定义函数Int(u，t)，其中u∈U，t∈T。综合考虑用户对标签偏好值和标签权重对用户标签兴趣度的影响，将标签偏好值Pre(u，t) 和标签权重Wu，v(t) 进行线性组合，函数Int(u，t) 计算公式为

Int(u，t)=α×Pre(u，t)+β×Wu，v(t)

(18)

式中：α和β分别表示用户对标签偏好值和标签权重的权重，α和β的具体取值在实验结果中得出。

3 基于标签挖掘的个性化推荐算法

3.1 用户标签兴趣相似度

用户标签兴趣相似度被用来衡量用户之间的兴趣相似性的大小，如果两个用户之间的标签兴趣相似度越大，那么表示他们的兴趣更为相似，反之则相反。定义函数Sim(uj，uv)，其中uj∈U，uv∈U。计算公式如下

(19)

式中：Int(uj，tl) 和Int(uv，tl) 分别代表用户uj和用户uv对标签tl的兴趣度，Tj，v表示用户uj和用户uv共同使用过标签的集合。

3.2 改进的SVD++模型

SVD++模型是在BiasSVD模型基础之上，根据实际推荐中用户评分行为较少来进行改进的，进一步引入隐式反馈信息。在隐式反馈中，假设存在一个与每个用户进行过隐式交互的物品集合相对应的k维隐向量。通过将与用户有过隐式交互的物品的隐向量相加，可以从一个新的维度来表示用户的兴趣爱好。这种改进方法能够提升一定的模型性能，但是还存在着不足。首先，没有考虑社会化标签的使用网站中存在“马太效应”。其次，用户对物品打分后，使用的标签在一定程度上反映出了用户对于该标签的喜好程度，物品评分能够类似于标签所占权重。对此，标签评分权重往往被忽视。

为解决以上问题，在SVD++算法模型的基础上将用户标签兴趣相似度引入其中，对SVD++算法模型进行改进。通过利用用户标签兴趣相似度，可以计算用户之间的相似度。这种改进方法具有以下优势：首先，在计算用户对标签偏好时，能够更准确地考虑到他们的兴趣相似度，考虑社会化标签的“马太效应”，对热门标签进行了数值惩罚，在一定程度上能够缓解“马太效应”。其次，通过物品评分来计算出标签权重，并引入最终的用户对于标签的兴趣度，使得最终结果更加具有泛化性。改进后的计算公式为

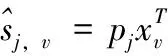
(20)

损失函数用于衡量模型预测评分与实际评分之间的差异。模型的准确度与损失函数值呈负相关，即模型准确度越高，损失函数值越小。然而，过小的损失函数值可能导致模型出现过拟合，从而降低了其泛化能力。为了提高模型的泛化能力，引入正则项用于限制损失函数的下降幅度，确保在具有较高预测精度下，模型仍具备良好的泛化能力。计算公式如下

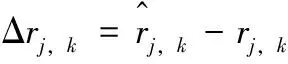
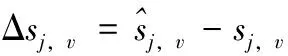
(21)

使用随机梯度下降(stochastic gradient descent，SGD)法进行参数迭代，直到测试集误差不在变化。公式如下

(22)

(23)

(24)

(25)

(26)

3.3 算法步骤

本文所提出的基于标签挖掘的个性化推荐算法记为PRMT模型，该算法大体分为输入和输出两步，根据用户、物品、标签和评分生成用户-物品评分矩阵、用户-标签评分矩阵和用户-标签交互矩阵。算法流程如下：

算法：基于标签挖掘的个性化推荐算法

输入：R：用户-资源评分矩阵；P：用户-标签评分矩阵；Y：用户-标签交互矩阵；正则化系数λ、权重系数λ1，α，β和学习率η

步骤：S1：读取数据并划分训练集和测试集，根据式(9)～式(11)分别构建用户-物品评分矩阵R、用户-标签评分矩阵P和用户-标签交互矩阵Y；

S2：根据式(12)～式(16)计算用户对于标签偏好值；

S3：根据式(17)计算用户标签权重；

S4：利用S2和S3计算所得值，根据式(18)计算用户标签兴趣度；

S5：利用S4计算所得值，根据式(19)用户间偏好相似度；

S6：将SVD++模型进行改进，将S5所得的用户偏好相似度带入改进后的SVD++模型，即本文所提算法模型PRMT；

S7：训练PRMT模型，根据式(20)～式(26)训练迭代参数，来寻找各参数的最优值，若模型迭代达到损失函数阀值，则进行S8，否则继续本步骤；

4 实验及结果分析

4.1 衡量标准

为了衡量本文提出算法模型效果，使用均方根误差(root mean square error，RMSE)和平均绝对误差(mean absolute error，MAE)进行检验，作为实验结果衡量标准。反映测试值与真实值之间的误差，RMSE和MAE值的大小与推荐精度呈负相关，即RMSE和MAE值越小，推荐精度越高。RMSE和MAE计算公式如下

(27)

(28)

4.2 数据集

本实验采用MovieLens数据集中的ml-25M，ml-25M数据集是MovieLens数据集中最大版本，包含了25 000 096条评分数据和1 109 927条标签数据，以及58 000部电影和280 000名用户，包括多个用户对电影的评分和标签，电影评分范围在0.5～5之间。同一用户可以给多个电影标注不同标签，且同一电影可以被不同用户标注不同标签。

对于数据集的处理，首先，我们利用用户编号和电影编号作为合并字段，将标签编号合并到含有用户编号、电影编号和评分的文件中；其次，对标签使用次数进行统计，将使用次数低于5次的标签以及所在行的全部数据删除，对处理后标签数据重新进行编号；最后，检查处理后的数据，查看是否有异常值或空值，然后保存到新文件中，用于后面模型训练。部分具体数据示例见表1。

表1 部分处理后数据集展示

4.3 参数确定

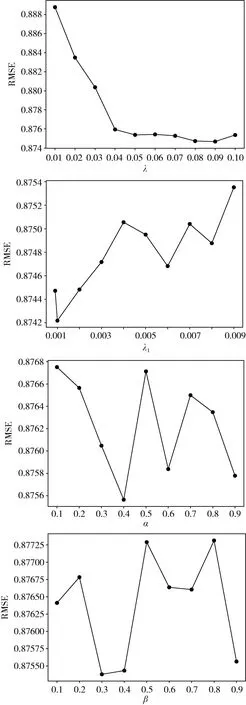
图2 各参数实验结果

根据图2中的实验结果曲线变化，可以得出：

(1)不同参数值的情况下，RMSE的值有增有减，其变化规律趋势无法确定。从图中变化曲线我们可以看出，对于参数值的选择不能一味的增大或减小，只有通过大量实验，选择最为合适的参数值，才能保证模型预测精度达到最佳。

(2)当α=0.4，β=0.3，λ=0.09，λ1=0.001时，RMSE的值最小，算法模型的精准度最大。

4.4 多模型之间推荐结果对比

本文选择对比模型有，LFM、SVD++、概率矩阵分解[15](PMF)、电影相似性协同过滤推荐模型[16](UB-HUS)、信任感知和领域专家的协同过滤模型[17](TrustMF)、个性化马尔可夫链和社交网络联合模型[18](JSR)、基于概率矩阵分解的协同过滤模型[19](IC-US-PMF)、用户标签相似度的矩阵分解模型[20](UTagJMF)，进行对比实验，实验结果如图3所示。

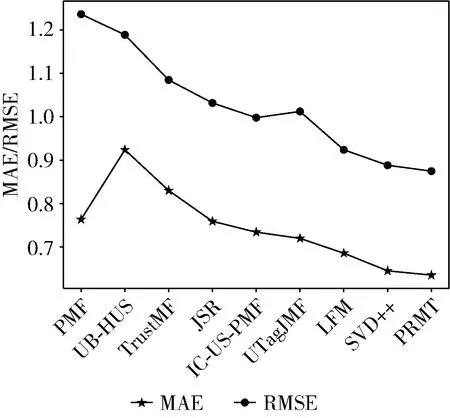
图3 不同模型之间对比

根据图3曲线变化，可以得知，PMF模型的RMSE和UB-HUS模型的MAE预测精度均为最低。模型TrustMF、JSR、IC-US-PMF、UTagJMF的MAE和RMSE值都有所下降，但都没有低于模型LFM和SVD++，而本文所提模型PRMT的RMSE和MAE值是最低的。

对此，将与本文所提模型PRMT性能最为相近的两个模型LFM和SVD++作为基准对比模型，将其单独拿出与PRMT模型对比RMSE和MAE。结果如图4所示。

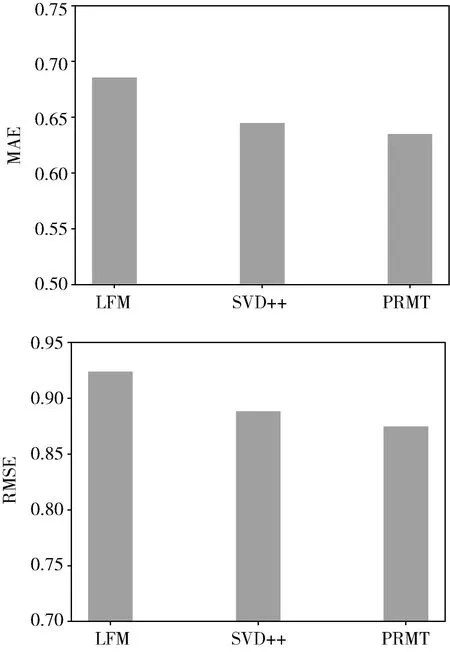
图4 3种模型之间比较

根据图4实验结果，能够得出以下结论：

(1)3种模型中，LFM模型RMSE和MAE值依旧最大，分别为0.9242和0.6855，模型预测精度依然最低。

(2)SVD++模型RMSE和MAE分别为0.8883和0.6448，相对于LFM模型预测精度提升4.04%和4.07%；PRMT模型RMSE和MAE分别为0.8742和0.6348，相对于LFM模型和SVD++模型预测精度在RMSE分别提升了5%和1.41%，MAE分别提升了5.07%和1%。

(3)3种模型在ml-25数据集上，PRMT模型RMSE和MAE值最小，表明预测精度最高。由此可见，本文算法模型明显优于其它几个模型，具有良好的预测精度。

5 结束语

推荐系统目前在各个领域都有所应用，矩阵分解算法是推荐系统中一个重要算法。本文所提算法，主要从用户对于标签的偏好值和标签权重来进行融合实验，在一定程度上挖掘出了用户更深层次的兴趣，算法综合考虑标签对于推荐精度的影响，同时对传统算法模型进行了改进，在一定程度上提高了推荐精度和改善推荐效果。

对于后续研究可以利用神经网络来深入挖掘用户兴趣的潜在特征，进一步提高推荐精度和效果。