谐波激励下压气机叶片多模态耦合振动特性研究

李 鑫,陈官峰,秦秀云,程 前,潘 容,2,王春健,张呈波

(1.中国航发四川燃气涡轮研究院,成都 610500;2.南京航空航天大学 能源与动力学院,南京 210016; 3.天津航天瑞莱科技有限公司,天津 300450)

作为航空发动机中的关键零件,随着发动机性能的不断提高,发动机叶片在工作过程中承受的载荷也越来越大。在所有发动机研制和使用过程中,几乎都发生过叶片振动问题,叶片振动故障大约占发动机结构故障的三分之一[1-3],因此在发动机研制阶段,必须对发动机叶片的振动疲劳特性进行充分的研究分析及试验验证。

航空发动机压气机叶片在工作环境中受到发动机高低压转子基频、来流尾迹等多个激励源的影响,发动机叶片在工作时很可能被同时激起多阶模态,形成多模态耦合振动,进而导致叶片出现高周疲劳断裂故障。目前工程上一般采用振动台对进行叶片的振动疲劳特性及性能进行测试,试验时通过多个工装将试验件安装在振动台上,振动能量传递时经过工装连接位置的多个摩擦界面。这使得振动台的简谐激励信号在传输过程中会出现谐波分量。基于此可以利用振动台形成多模态共振,用以研究叶片的耦合振动。

国内外多位研究学者对谐波振动特性进行了研究,胡家顺等[4]研究了呼吸裂纹梁在外部激励下的谐波振动特性,在众多谐波分量中,接近系统频率的谐波其能量幅值大于远离系统频率的谐波。蔡逢春等[5-6]研究了裂纹梁在简谐激励下的动力学特性,在较大幅值的简谐激励作用下,会激起结构的几何非线性,系统相应也会出现谐波成分。马晓峰等[7]研究了叶冠间接触的动力学特性,碰撞使得叶片的振动响应产生许多高频分量,使得能量分散在各频谱上,而不是集中在激振频率或者固有频率上。韩刚等[8]研究了航空发动机压气机含呼吸裂纹叶片在转子位移激励下的动力学特性,发现裂纹导致系统存在多种联合共振响应。Johnson等[9]研究了一个单自由度双刚度理论模型,并进行了裂纹梁的有限元分析,表明激励频率接近两倍线性固有频率时亚谐波成分明显。

在振动响应分析方面,田少杰等[10]研究了气流激励下叶片振动响应分析方法,通过模态叠加法对转子叶片强迫振动响应进行了分析。Jia等[11]采用一种基于时域系统识别的方法分析了涡轮机械的耦合模态。Ghasemloonia等[12]采用线性轴向-横向耦合动力学模型分析了钻井钻头在旋转过程中的横向耦合振动。K Hayat等[13]采用时域分析的方法分析了弯扭耦合大型风力涡轮机叶片的颤振性能。Chen等[14]基于模态分解方法揭示了大型柔性管道多模态共振过程中的振动特性。Chen等[15]提出了一种基于模态能量的预测方法分析了剪切流作用下细长电缆的多模式涡激振动。

虽然目前已有大量关于谐波振动的文献,但是主要集中在理论研究方面,对于谐波共振产生的条件没有进行深入的探索。同时关于叶片谐波振动相关的试验研究较少,且没有对由于谐波振动导致的叶片多模态耦合共振现象及响应分析进行研究。

本文通过开展航空发动机叶片振动疲劳试验,研究了叶片多阶模态耦合振动时的振动特性,基于振型叠加法获取了叶片在多模态耦合振动下的振动应力。通过分析不同叶片的耦合振动特性的差异,探索了叶片发生谐波共振的频率阈值,给出了叶片设计时激振频率倍频与固有频率之间的设计裕度。

1 试验件设计与试验方法

1.1 试验件设计

当发动机叶片的高阶固有频率与低阶固有频率的倍频的频差很小时,利用振动台的简谐激励信号在多个工装的传输过程中出现高阶谐波分量的现象,通过激振频率谐波分量激起叶片高阶模态,进而发生多模态耦合振动现象。

基于上述的设计思路,本文采用有限元仿真的方法开展了叶片振动设计,设计出一种二阶频率与一阶频率的二倍频十分接近的叶片。叶片前6阶固有频率和模态计算结果如表1所示。前2阶振型及振动应力分布图如图1所示。根据表1的计算结果可以看出,叶片第2阶固有频率与第1阶固有频率二倍频的频差仅为9 Hz,因此在振动台上采用叶片1阶固有频率作为激振频率进行高周疲劳试验时,会出现激振频率的二次谐波响应,从而诱发叶片一二阶振型耦合振动的现象。

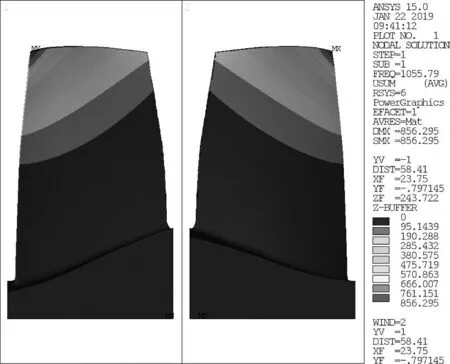
(a) 一阶振型

表1 前六阶固有频率

1.2 试验件装夹

为了便于试验件安装,在试验件底端设计了两个相互平行的夹持面,图2给出了叶片的结构示意图。试验时夹持块通过8个M12的螺栓沉孔与振动台连接;夹持块通过2个M12螺栓夹紧,配合4个M12螺栓将夹持面顶紧。

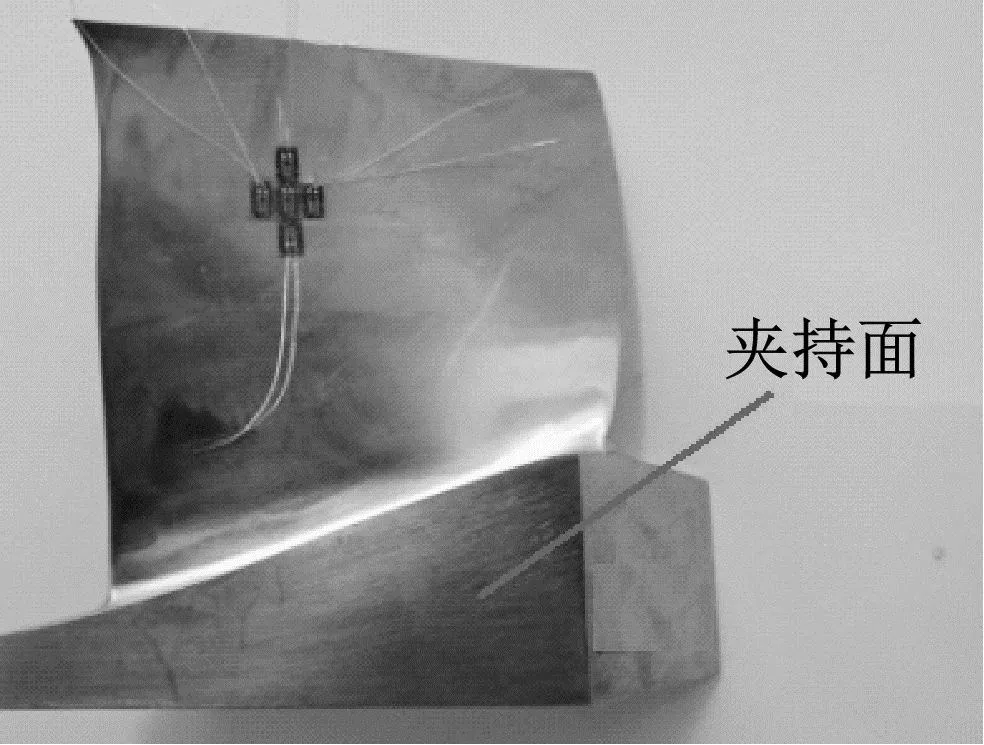
图2 试验件及装夹方式

1.3 试验方法

在进行高周疲劳试验时,叶尖幅值与叶身应变通常呈线性关系,长时的疲劳试验中应变片通常会失效,为持续监测试验过程中叶片的振动应力水平,在小应变水平时对叶尖幅值和应变片幅值进行标定,实际开展疲劳试验时采用激光位移传感器测取叶片振动幅值,间接测量叶片的振动应力。图3给出了叶片试验现场图。

注:1.试验件; 2.振动台; 3.激光位移传感器。

试验时首先对叶片开展多阶次模态位移-应变标定试验,首先记录叶片的振动疲劳试验中的叶尖位移信号和应变信号,其次利拟合得到各阶振型的位移和应变的转换关系,最后获取多阶次模态位移与应变的标定拟合曲线以及叶片的振动特性。

2 试验结果与分析

2.1 多阶次标定试验结果

由于谐波振动的影响,叶片在进行试验时已经不是在单一模态下进行振动,而是出现多模态耦合振动的情况。采用传统的单一模态位移应变标定的方法仅能换算得到叶片在激振频率下的振动应力,没有考虑叶片的谐波振动激起的高阶模态振动应力,且谐波振动响应与激励幅值存在明显的非线性关系,当激励达到一定程度后可能会出现高阶模态振动应力大于激振模态振动应力的情况,因此在进行试验时就需要考虑高阶模态的振动应力。

据叶片振动原理,叶片振动应力和弹性线的曲率成正比,对于确定的振型,其振型函数也是一定的,因此对于确定的振型,振动应力与位移也是成正比的。基于此本文提出了一种多阶次模态位移应变标定的方法,在进行标定时对叶片多阶模态振型同时进行标定,即在试验过程中不仅对激振频率下的位移应变结果进行标定,同时对谐波振动阶次下的位移应变结果也进行标定。图4给出了叶片标定试验中叶片应变测点位置示意图,速度测点选取的是叶身中部位置,应变测点选取激振频率下的叶片振动应力响应最大点G点以及谐波振动频率下叶片振动应力响应大应力区L点,其中L点的标定结果如图5所示。可以看出叶片在一阶振型(激振频率)和二阶振型(谐波振动频率)下的位移(速度)与应变均为线性关系,与理论结果一致。

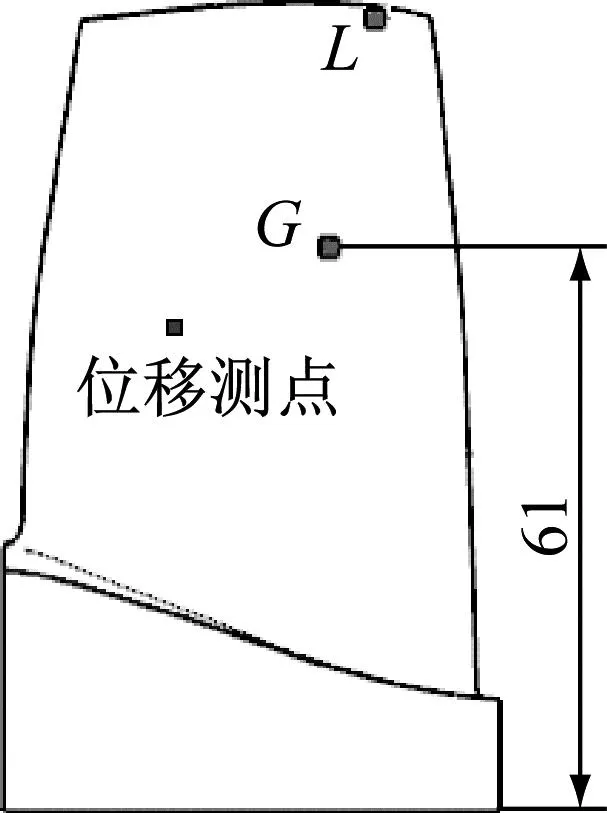
图4 应变测试位置

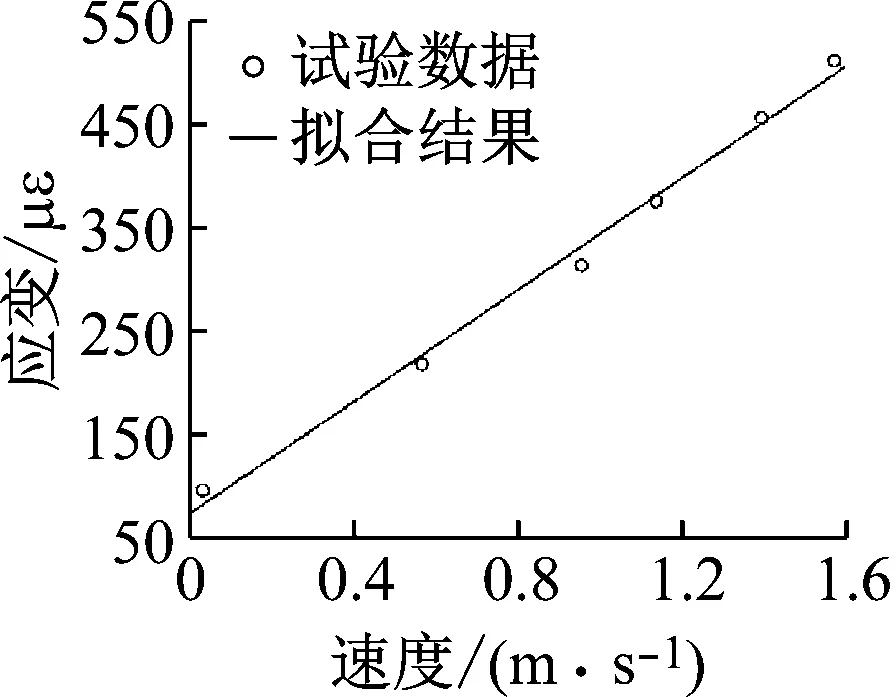
图5 叶尖L多阶次标定试验结果

2.2 谐波振动特性分析

叶片振动特性试验结果如图6所示。试验时叶片的激振频率为一阶固有频率,根据图6可以看出,试验时同时激起了叶片的激振频率以及激振频率的二次谐波频率,其中位移频谱图为激光位移传感器实测结果,应变频谱图为应变片实测结果。随着激振输入的持续增大,叶片的二次谐波应变幅值响应ε2f的增速大于激振频率的应变幅值响应εf,表2和图7给出了ε2f与εf的关系。根据图7可以看出二次谐波响应幅值与激振频率响应幅值的二次方呈线性关系,同时激振频率响应幅值和系统的激励幅值呈线性关系,因此可知二次谐波响应幅值与系统的激励幅值二次方也呈线性关系。

图6 振动特性试验结果

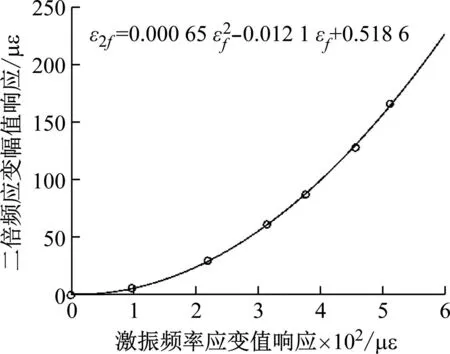
图7 谐波响应幅值与激励幅值关系

2.3 耦合振动响应分析方法

本文采用模态叠加法计算了叶片的振动响应。模态坐标系下的振动方程为

(1)

式中:yi为模态坐标;ωi为第i阶的系统固有频率;ζi为模态阻尼比;α为非线性项系数;gi为非线性项;fi为外载荷。

对于简谐激励,fi可以写为

fi=feieiΩt

(2)

式中:fei为简谐激励的复数幅值;Ω为简谐激励的频率。

根据2.2节的振动特性分析结果可知,叶片主要振动响应阶次为激振频率及激振频率倍频,根据试验结果发现,叶片的倍频响应主要为2倍频,3倍频和4倍频较小,其他倍频响应不明显,因此倍频成分本文主要考虑2、3、4倍频,忽略其余倍频成分,因此式(1)的近似解可以写为

(3)

式中:Yei为激振频率的复振幅;Yj·ei为倍频的复振幅;φj为激振频率响应与倍频响应的相位差。

同一阶次的位移和应变响应,其相位角是完全一致的,因此对于位移响应和应变响应,式(3)可以写为

(4)

(5)

式中,D和Ε表示位移和应变响应。

在获取位移响应后只需获取各阶振型下位移幅值和应变幅值的关系即可求得应变响应,即应变响应的结果为

(6)

式中:hi多阶次标定试验激振频率的位移应变标定结果;hj·i倍频下应变位移标定结果。

2.4 耦合振动响应分析结果

图8给出了叶片测量得到的位移响应时域/频谱图以及基于模态叠加法计算得到的应变响应时域/频谱图,可以看出试验叶片叶尖处的谐波振动响应已经超过了激振频率下(一阶)振动应力最大点的响应。对比叶尖L处及G点的应变时域曲线可以看出,不同时刻叶尖L处及G点的应变比值是不同的,这说明此时叶片已经不是在单一模态下的振动响应,而是发生了多模态耦合振动。此时叶片的危险点已经不是单一模态下的振动应力最大点,而是多模态振动应力叠加后的最大点,根据图8中叶尖与G点的振动应力时域曲线可以看出,叶尖L处的振动应力幅值已经是G点位置振动应力幅值的2倍。

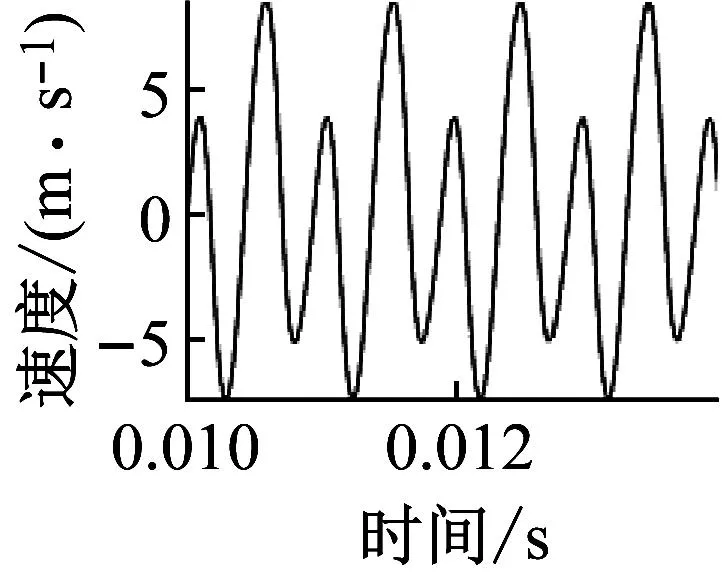
(a) 速度时域曲线-叶身中部

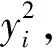
(7)

式中:ω0为固有频率;ω为激振频率。

当仅考虑前两阶振型时,可假设式(7)的解为

y(t)=Acosωt+Ccos 2ωt

(8)

式中,A和C分别为激励频率以及二次谐波分量的幅值。

将式(8)代入式(7)中可得

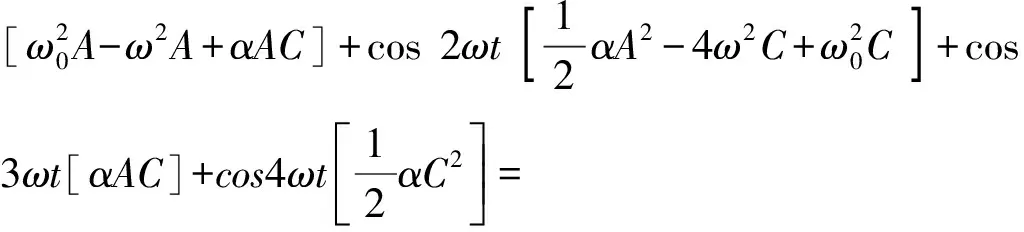
Fcosωt

(9)

由于响应结果仅包含激振频率及二倍频,因此忽略cos 3ωt和cos 4ωt的项,并令式(9)两边cosωt和cos 2ωt的系数相等,得:

(10)

(11)

根据式(11)可得

(12)

根据式(12)可知二次谐波分量的振幅与激励频率幅值的平方成正比,这与图7的试验结果相一致。当激振能量很小时,此时仅能激起一阶模态,叶片主要以一阶模态为主进行振动。随着激振能量的逐步增大,叶片的二阶模态逐渐被激起。由于二阶模态响应幅值与一阶模态响应幅值的二次方成正比,因此二阶模态响应的增速明显高于一阶模态。当激振能量足够大时,此时二阶模态响应已经远远大于一阶模态,叶片此时主要以叶片的二阶模态为主进行振动,整个过程就是叶片模态由一阶模态逐步向二阶模态转化的过程。

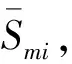
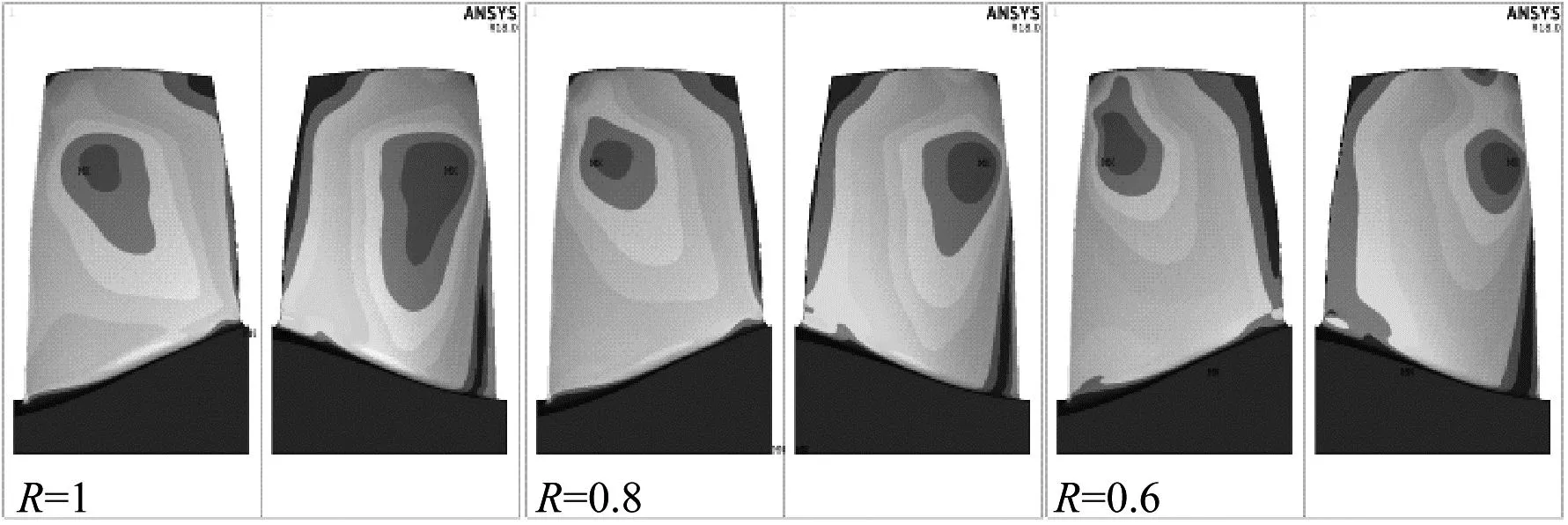
图9 模态叠加结果

图10给出了基于应变响应频谱图(R=0.15)计算得到的叶片相对振动应力分布图,可以看出叶片在一二阶同时出现共振时最大振动应力在叶尖位置L处,此位置为二阶振动大应力位置,且一阶振动应力也较为明显,在多阶模态耦合振动下叶尖位置L处的振动应力最大,最终振动疲劳试验结果显示此处出现裂纹。图11给出了叶片的断口分析结果,根据分析结果可知,断口呈明显的疲劳特征,其源区位于叶尖顶端与叶背侧的交角,点源,源区呈磨损形貌,裂纹从源区起始,向叶根、叶盆以及前缘方向扩展。裂纹传播的路径与理论分析的大应力区一致,验证了振动应力响应分析的正确性。

图10 耦合振动应力分析及试验结果

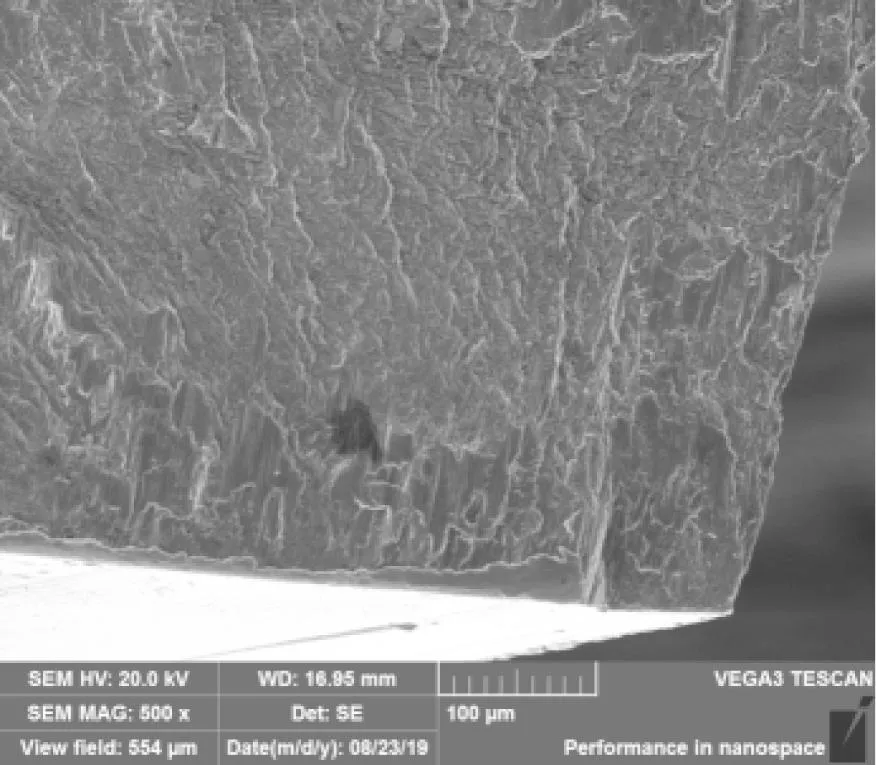
图11 断口分析结果

2.5 耦合振动特性分析

当高阶模态固有频率与谐波频率重合或者相近时,会发生谐波频率激起的高阶模态共振,谐波频率与高阶模态频差的大小直接决定了谐波振动响应的大小。为了进一步研究谐波共振发生的条件,本文选取9件试验件进行了谐波振动特性试验,表3给出了试验结果。其中f1为叶片的一阶实测固有频率,f2为叶片的二阶实测固有频率,2f1为叶片的一阶实测固有频率二倍频,δ2为一阶频率的二倍频与二阶频率的频差。为了便于后续分析,将谐波振动应变响应与激励频率响应的比值ε2/εf1定义为耦合系数m。

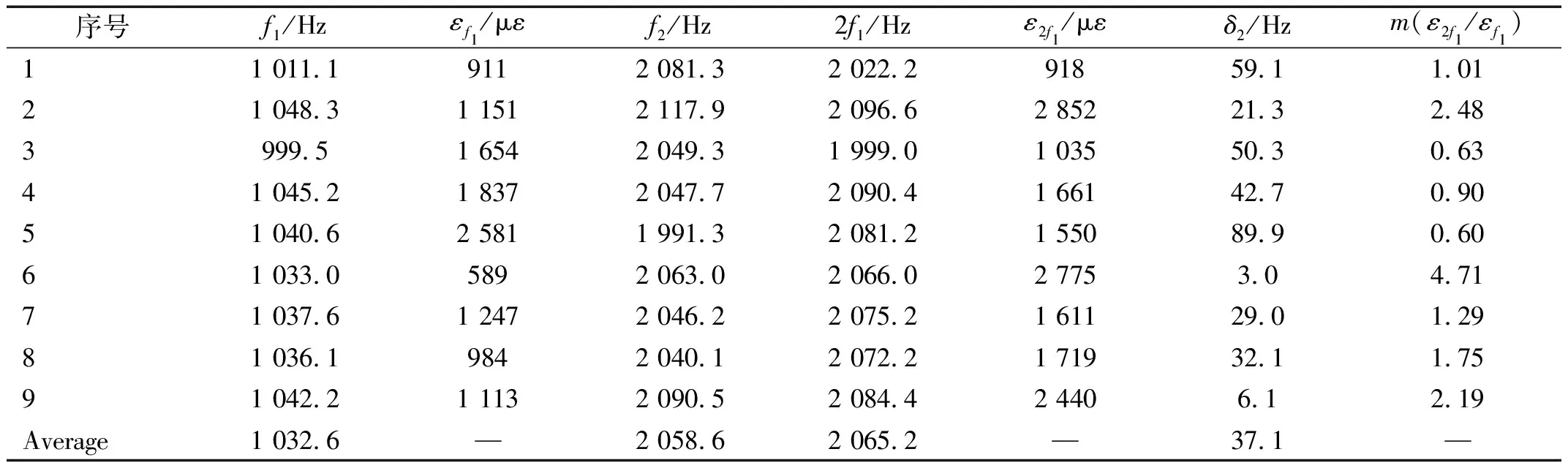
表3 耦合振动测试结果分析

根据航空发动机压气机叶片设计经验,为避免叶片发生耦合振动,其频率裕度应该大于10%,由于缺少大频差数据点,因此本文假定当频率裕度达到10%时不发生耦合共振,即耦合系数m等于0。基于此对耦合系数m随频差δ2的变化规律进行数据拟合分析,得到中值拟合函数为m2=4.275e-0.032 17δ2。图12给出拟合分析的结果,根据分析结果可知,当频差大于158 Hz即频率裕度(δ2/f2)大于7.68%时,耦合系数小于0.1,谐波振动的响应小于激励频率响应的10%,此时叶片发生耦合振动的可能性较小。

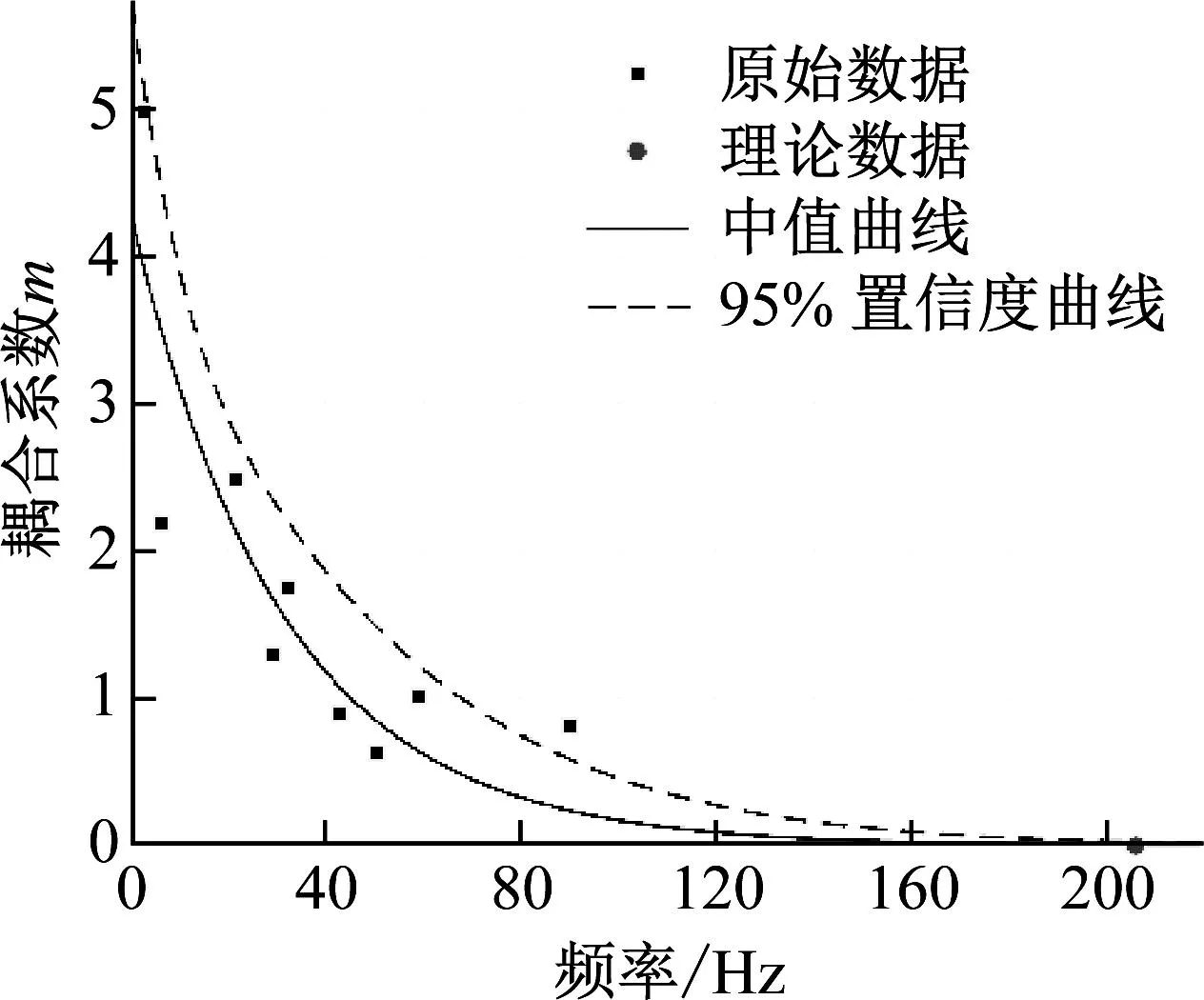
图12 耦合系数与频差之间的关系

考虑到压气机叶片复杂的工作环境,叶片受到的激励频率成分复杂,单个激励的形式不仅仅为简谐激励,也可能是脉冲激励、三角激励或形式更加复杂的激励。当这些激励的谐波分量与叶片固有频率接近时就很可能导致叶片存在多模态耦合振动的现象。因此在设计发动机叶片时,除了考虑激振频率和固有频率的频率裕度外,还需考虑激振频率倍频和固有频率之间的频率裕度,考虑到一定的数据分散性,建议激振频率倍频和固有频率之间频率裕度应大于8%。

3 结 论

基于航空发动机叶片多模态耦合振动特性,本文开发了一种叶片多模态耦合振动特性的测试及响应分析模型,得到了如下结论:

(1) 针对叶片存在多模态耦合振动的现象,提出在进行试验时同时对叶片的多阶模态进行标定试验,同步获取多阶模态叶片的位移应变关系。

(2) 获取了叶片谐波振动特性的特点。当叶片的高阶模表态频率与叶片的激振频率的倍频相近时,叶片会出现明显的谐波振动响应。随着激振能量的逐渐增加,谐波振动的响应增加速度明显大于激振频率的响应,二次谐波响应幅值与激励幅值二次方呈线性关系。

(3) 给出了叶片多模态耦合振动响应的测试及分析方法。基于标定结果和模态叠加法,给出了耦合振动下叶片的响应分析方法,并根据方法计算得到叶片振动应力最大点位于叶尖位置,试验结果与理论分析结果一致,验证了分析方法的有效性。

(4) 探明了叶片谐波共振发生的条件。随着谐波频率与叶片高阶固有频率频差的逐渐增大,谐波共振的响应以指数形式下降,当频率裕度大于7.68%时,谐波振动的响应小于激励频率响应的10%,此时叶片发生耦合振动的可能性较小。因此在设计发动机叶片时,除了考虑激振频率和固有频率的频率裕度外,还需考虑激振频率倍频和固有频率之间的频率裕度,考虑到一定的数据分散性,建议激振频率倍频和固有频率之间频率裕度应大于8%。