基于密度的凹版专色叠印色光谱预测模型的研究及应用

张宜洋，郭凌华，武城运，海敬溥，王荣欣，陈睿

基于密度的凹版专色叠印色光谱预测模型的研究及应用

张宜洋1,2，郭凌华1,2*，武城运1,2，海敬溥1,2，王荣欣1,2，陈睿1,2

（1.陕西科技大学 轻工科学与工程学院，西安 710021； 2.中国轻工业功能印刷与运输包装重点实验室，西安 710021）

建立一种基于密度与光谱反射率关系的专色叠印色光谱预测模型。首先建立前景色、后景色密度与其光谱反射率关系；基于此建立叠印色光谱反射率的计算方法；其次对模型进行优化，完成专色叠印色光谱预测模型的建立；再通过凹版印刷实打样30张专色叠印色样张，基于Malab利用色差以及拟合决定系数2对预测模型进行验证；最后在相同工艺条件下实打样专色叠印色样张进行预测，通过色差完成对模型的精度检验。验证表明，不同专色叠印色在同一网点面积率下与其对应的前景色、后景色密度之间存在较强相关关系，其拟合决定系数2均大于0.9；模型精度检验中，73.7%的模型预测值与样张实测值色差为0～2.5个CIE1976色差单位，大部分色块色差为0～2个CIE1976色差单位，占总频率的60.54%，整体平均色差为1.92个CIE1976色差单位。本文所建模型具有较高的预测精度，能基本满足对颜色预测的需求。

专色叠印；油墨密度；光谱反射率；预测模型

凹版印刷因其色彩丰富、适用性广以及防伪效果强等优势被广泛应用于包装印刷。许多厂商在进行产品设计时常将专色叠印色应用于包装产品中，旨在增强防伪效果和刺激消费者的购买欲望，专色叠印色在包装印刷中应用广泛。然而，目前针对专色颜色预测的研究多基于专色实地或专色阶调，对专色叠印色预测的颜色模型较少，如经典的Kubelka-Munk[16-18]理论多用于专色实地印刷的颜色预测以及验证专色油墨配方的准确性，无法应用于专色叠印色的颜色预测。传统四色叠印预测模型多基于Neugebauer方程[1-7]，但由于专色数量庞大，传统叠印预测模型应用于专色叠印预测时存在着计算复杂、需求样本数过多等问题。因此，开发一种能够精确预测专色叠印色、具有高精度且计算简便的专色叠印色预测模型具有重要意义。

随着专色叠印色在包装市场的需求日益增加，关于专色叠印色预测模型的研究也开始兴起。目前，国内学者杨慧芳等[8]通对专色和叠印色分别进行光谱分析的方法，模拟两者之间的关系，对光散射、叠印率、透明度等物理因素进行修正，建立了专色叠印预测模型。国外学者Van de Capelle等[9]以方程系数来表达油墨叠印率、透明度、光的散射透射等因素对呈色的影响，通过预先设计色靶求出系数，代入方程系数完成对不同颜色叠印后光谱值的预测。此外，Deshpande等[10]开发了一种专色叠印预测模型，该模型通过预先设计色靶，经分析求解得到专色三刺激值以及对应网点面积率的相关系数，从而完成专色叠印色的预测。上述模型均计算简单且精度尚可，但都是应用于胶版印刷的预测模型，是基于半色调呈色的预测模型。然而，凹版印刷通过半色调与墨层厚度相结合的方式呈色，对特定颜色的油墨，印刷厚度不同则油墨的吸光能力不同，导致颜色密度不同[11]。因此，在凹版专色叠印色预测中，这些模型的使用不可避免地会产生一定的误差。

综上所述，颜色密度能更准确地反映凹版印刷半色调与墨层厚度相结合的呈色特性。因此，本文通过研究密度与光谱反射率的关系建立前景色、后景色、叠印色三者间密度关系，基于此关系结合光谱密度与光谱反射率建立凹版专色叠印色光谱预测模型。

1 专色叠印预测模型

1.1 叠印色计算

当光线照射到反射物体表面时，由于物体表面结构的多样性，导致了选择性吸收的形成。可见光谱中特定波长被吸收，其余波长则被反射。可通过反射物体的光谱反射率（比）来量化选择性吸收这一特性，即利用反射光通量p()与入射光通量0()之比来描述，其准确地反映了反射物体对各波长单色光的反射比例，是波长的函数。()的定义为：

类似地，可以使用反射物体的光谱密度来表示其对光的吸收量：

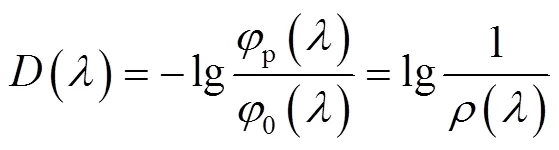
由式（2）可将物体的光谱密度转化为光谱反射率，具体如式（3）所示。

因此，就一具体专色叠印色而言，其前景色、后景色以及叠印色光谱反射率对应的光谱密度可表示为式（4）～（6）。

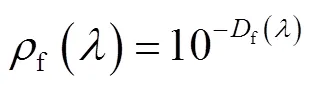
对比式（4）、式（5）和式（6）表达式可知，通过借助前景色、后景色光谱值以及对应的主密度值，对前景色、后景色光谱反射率进行次方即可实现对专色叠印色光谱值的预测。具体如式（7）所示。

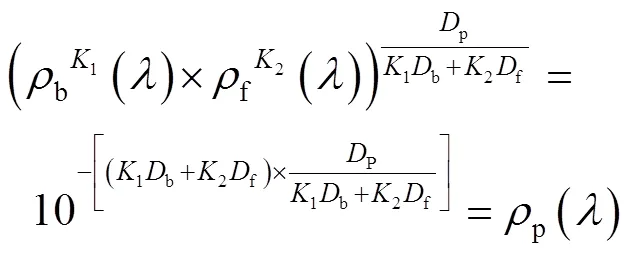
式中：p()为叠印色光谱反射率；b()为后景色光谱反射率；f()为前景色光谱反射率；p()为叠印色光谱密度值；b()为后景色光谱密度值；f()为前景色光谱密度值；1、2为模型比例系数。

式（7）通过对前景色、后景色光谱反射率进行次方变化，可得专色叠印色光谱反射率为前景色、后景色光谱反射率次方的乘积。利用此公式可在已知前景色、后景色光谱值时预测叠印后所得专色叠印色的光谱反射率值。但印刷时承印物对油墨呈色的影响不可忽视，而式（7）并未考虑承印物因素，因此将引入相对密度来对模型进行优化，并完成预测模型的建立。

1.2 专色叠印色光谱预测模型的建立

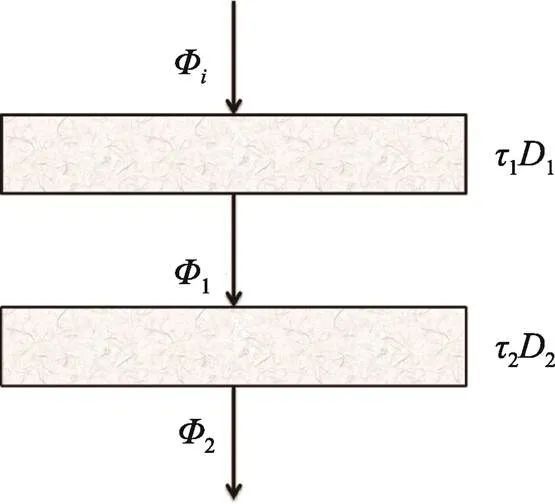
图1 密度叠加计算

则当光连续穿过2层物质后合成透射率与合成密度值分别见式（8）、式（9）。

合成透射率：

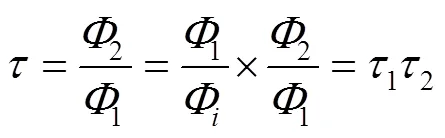
合成密度：

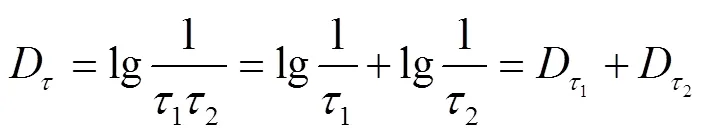
即光通过2个物体后的合成透射率为对应物体透射率之乘积，合成密度为对应物体密度之和。又因为光透射率与光密度均为光谱波长的函数，所以可将式（1）、式（2）分别写成：

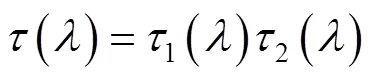
式中：()为光谱透射率；D()为光密度。

在凹版印刷中，油墨以一定的厚度附着于承印物之上来表现颜色，即实验测量所得密度均为墨层厚度与承印物的叠加密度[11]。则由式（11）可知，叠印色、后景色、前景色的相对密度见式（12）。

假设前、后景色密度与叠印色密度之间的关系为：

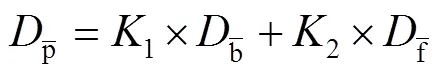
则在承印物上得到的叠印色密度为：

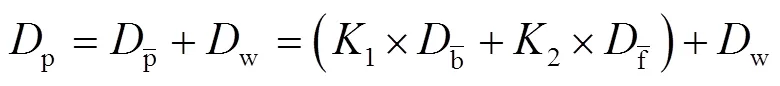
结合式（7）可得式（15）。

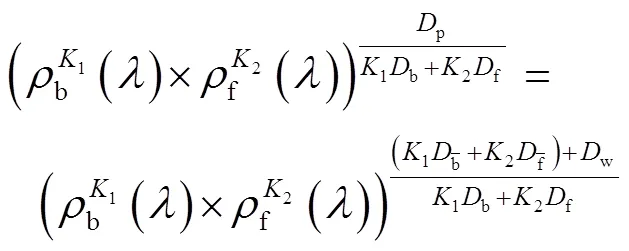
将式（12）带入式（15）化简可得最终模型式（16）。

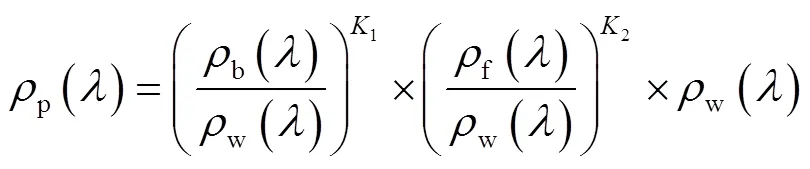
式中：p()为叠印色光谱反射率；b()为后景色光谱反射率；f()为前景色光谱反射率；w()为承印物光谱反射率；1、2为前景色、后景色与叠印色的比例系数。

1.3 预测模型评价方法及指标

对于该模型的验证，可利用Matlab函数拟合工具箱中自定义方程功能完成。导入对应专色光谱反射率数据后，通过最小二乘法，以式（16）为拟合函数得到2最大时1、2值。多项式拟合中通过样本的决定系数2表示回归拟合程度的好坏。2的取值范围为0～1，其值越接近于1，说明拟合效果越好。

另外可使用光谱均方根误差和色差2个参数来评价模型性能。选择不同凹版专色进行叠印，实打样凹版专色叠印色样张并测量其光谱值、Lab值，通过模型计算得到预测专色叠印色光谱值，计算预测色与实打样色光谱均方根误差，预估预测结果的准确性。最后依据式（17）、式（20）将预测色光谱值转化Lab值与实打样样张测量所得Lab值基于式（22）计算CIE1976Lab色差[13-15]，完成对模型的性能评价。

其中：

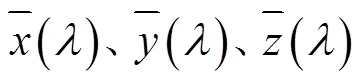
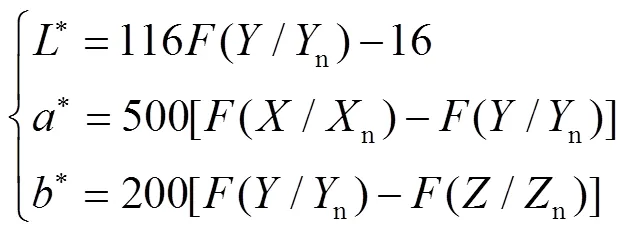
式中：、、分别为测量三刺激值；n、n、n分别为CIE标准照明体三刺激值；*、*、*分别为CIE Lab颜色值。

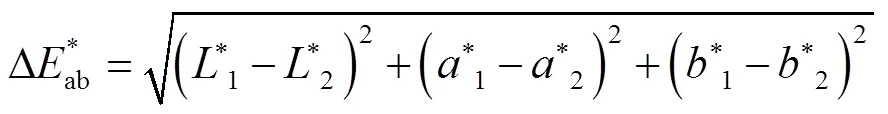
2 实验结果与分析

2.1 样张输出与数据采集

选取凹版雕刻工艺参数：扁菱形网穴，70线，120°针，以5%网点面积率为间隔雕刻专色叠印色试验凹印版。选择里印工艺，以PET薄膜为承印物，选取60种不同的专色油墨，利用三正精机凹印打样机两两叠印输出30张叠印色样张。具体过程：利用预先雕刻的凹印版印刷前景色、清洗并顺时针旋转印版180°、印刷后景色、在薄膜上实地印刷一层白色基底，从而得到如图2所示的叠印样张。

图2 叠印色样张示意图

在平整台面上将白色纸张垫于薄膜下，使用爱色丽分光光度计测量所有样本的Lab值、密度值以及光谱反射率，对同一样本取3次测量的平均值作为样本的最终测量值。测量条件为D50光源，10°视场；光谱反射率波长为400～700 nm；采样间隔为10 nm。基于测量数据，绘制部分专色叠印色光谱反射率与前景色、后景色光谱反射率乘积曲线，如图3所示。

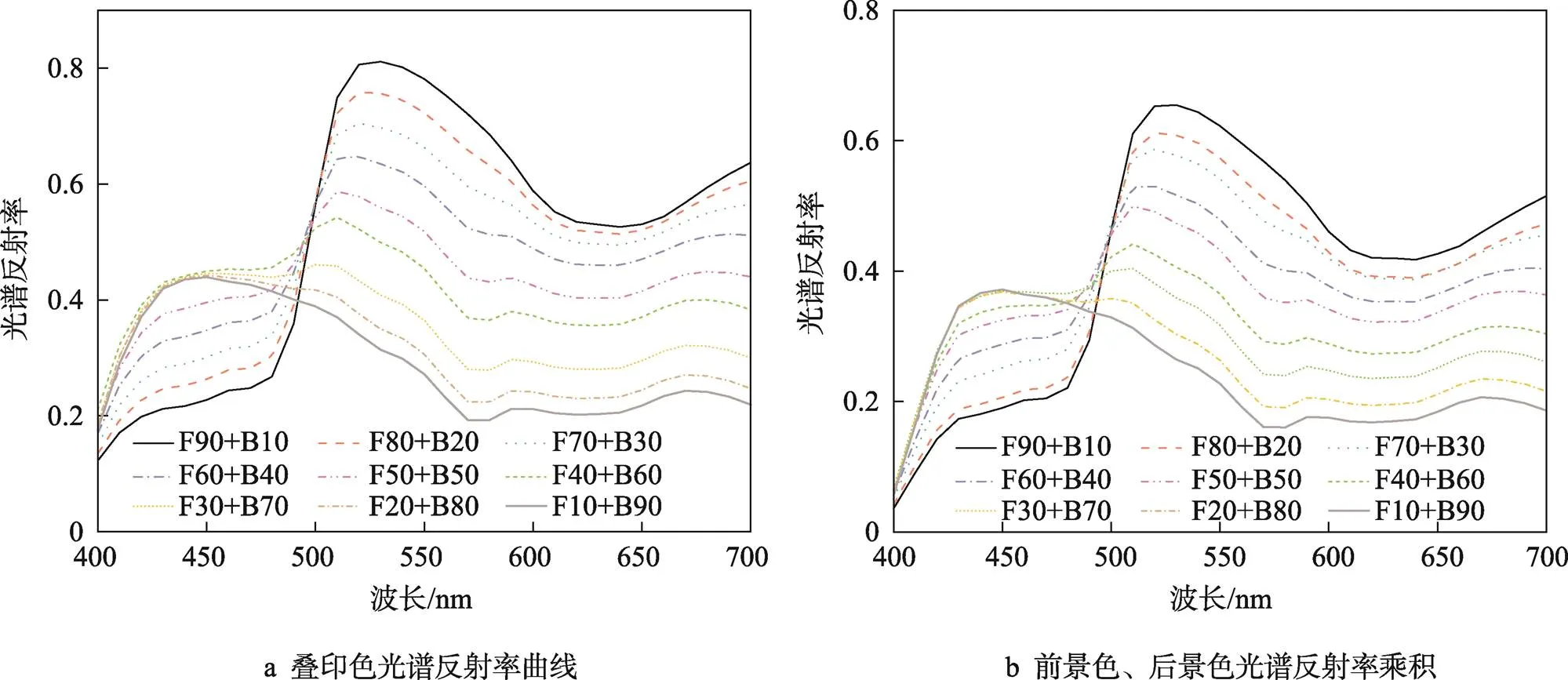
图3 专色1三者光谱反射率关系曲线

图3a为叠印色专色1光谱反射率曲线；图3b为专色1叠印前对应前景色、后景色光谱反射率乘积曲线。图3a中曲线F90+B10表示网点面积率为10%的后景色与网点面积率为90%的前景色叠印后所得专色的光谱反射率曲线；图3b中曲线F90+B10则为叠印前，对应网点面积率后景色、前景色两色光谱反射率乘积，图3中其他线段含义诸如此类。从图3中不难看出前景色、后景色光谱反射率乘积曲线与叠印色的光谱反射率曲线变化趋势十分接近，即前景色、后景色光谱反射率与叠印色光谱反射率存在相关关系。

2.2 前景色、后景色与叠印色密度关系验证

将30张叠印色样张测量所得前景色、后景色和叠印色密度值减去对应承印物密度值得到三者实际密度值；将所得实际密度值导入Matlab中，利用函数拟合工具箱以式（13）拟合，得到确定系数2以及模型比例系数1、2。具体拟合结果如表1所示。

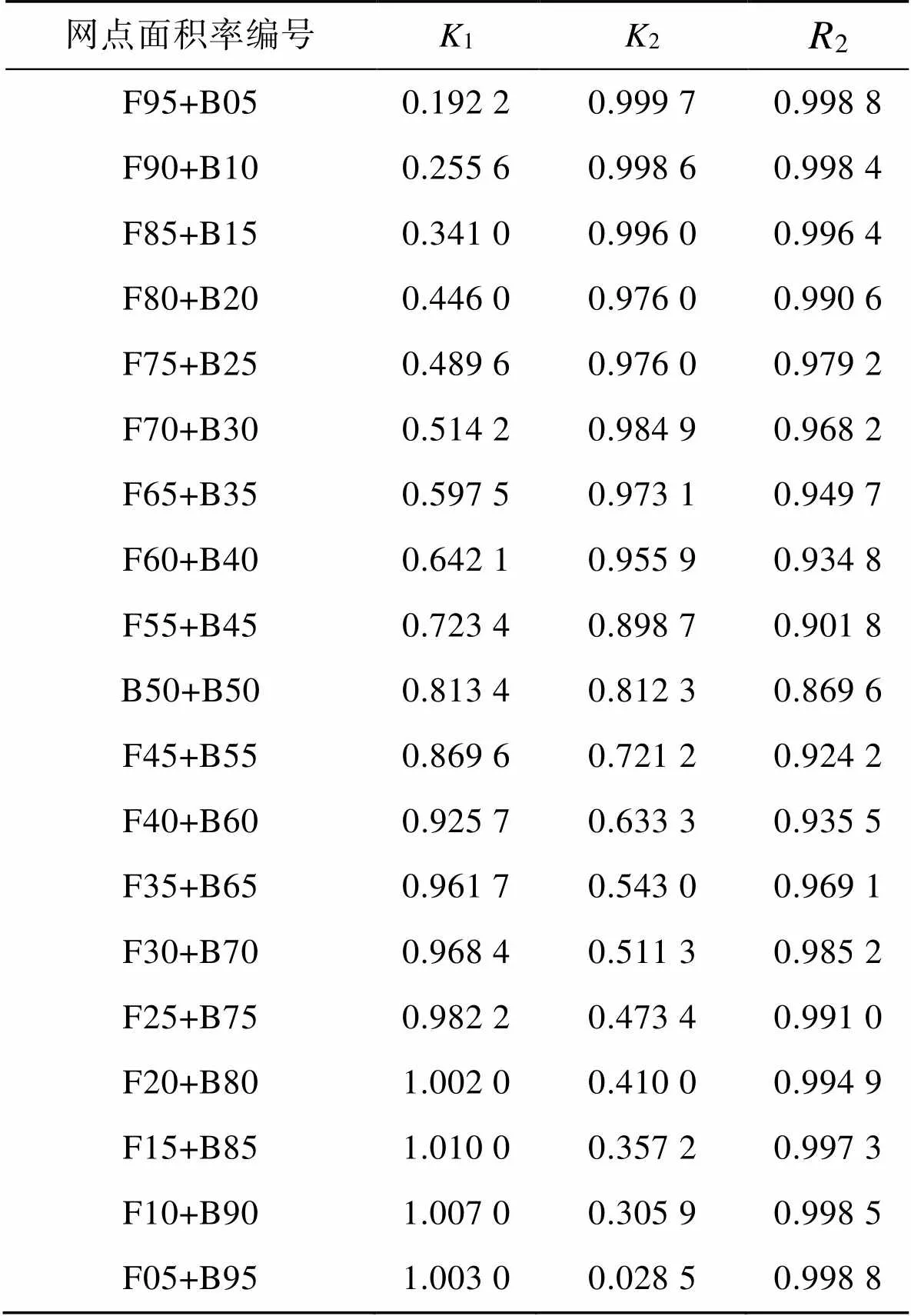
表1 密度关系拟合结果

Tab.1 Fitting results of density relationship

注：表中F95+B05表示以前景色网点面积率为95%叠印后景色网点面积率5%，其他编号以此类推。

从表1中可以看到绝大部分网点面积率下的前景色、后景色以及叠印色三者密度之间的决定系数2均大于0.9，即在相同网点面积率下三者拥有较强的相关性。通过实验验证可知，在印刷条件一致的前提下，当网点面积率相同时，不同专色油墨叠印色密度与前景色、后景色密度存在比例关系。

2.3 专色叠印光谱预测模型验证

前文利用Matlab验证了不同专色油墨的前景色、后景色与叠印色密度之间存在着比例关系，并基于此结合密度与光谱反射率的关系建立了专色叠印色光谱预测模型。实验中选取的光谱反射率范围为400～700 nm，并以10 nm间隔为一组31维的数据，通过函数拟合的方式来验证模型的可行性。表2、表3为2个不同专色叠印色的拟合结果与色差，其中1、2为拟合所得的比例系数，2为拟合决定系数，RMSE为光谱均方根误差，∆为CIE1976色差值。首先利用函数拟合工具箱拟合得到模型比例系数1、2；然后将其带入专色叠印光谱预测模型计算预测光谱反射率，并通过式（17）、式（20）转换为Lab值；最后利用式（22）与实测值计算得到色差。

表2 叠印专色1拟合结果及色差

Tab.2 Fitting results and color difference of overprint spot color 1

注：表中前景色密度为=0.713 5、=0.539 6、=0.406 3、=0.636 2；后景色密度为=0.241 7、=0.110 8、=0.559 9、0.1656；叠印色密度为=0.248 7、=0.117 3、=0.567 6、=0.172 3。

表3 叠印专色2拟合结果及色差

Tab.3 Fitting results and color difference of overprint spot color 2

注：表中前景色密度为=0.236 0、=1.708 5、=0.960 1、=0.646 2；后景色密度为=0.128 8、=0.317 6、=0.809 0、=0.247 2；叠印色密度为=0.233 1、=1.699 4、Y=0.957 1、=0.642 7。

表2、表3中可以看出，专色在不同网点面积率下决定系数均大于0.98，大部分网点面积率处光谱均方根误差小于0.01，即专色在不同网点面积率下均有较高的拟合度。利用公式将预测光谱值转化为CIE1976色差后，最大色差为2.966、平均色差为1.358基本满足专色复制要求。证明了本文建立的专色叠印光谱预测模型具有可行性，存在确定的比例系数使预测模型成立，能较为准确地预测叠印色光谱反射率。同样的若已知比例系数，则可利用比例系数完成对专色叠印色的光谱预测。

综上所述，本文所建专色叠印光谱预测模型在取得合适的1、2值时具有较高的预测精度。为了更直观准确地测试模型性能，可利用表1拟合所得1、2值。选择20种不同专色油墨两两叠印，在相同工艺条件下进行实打样输出10张专色叠印色样张。通过计算模型预测值与样张实测值色差评价模型性能，验证结果中190个叠印色块色差频率分布如图4所示。

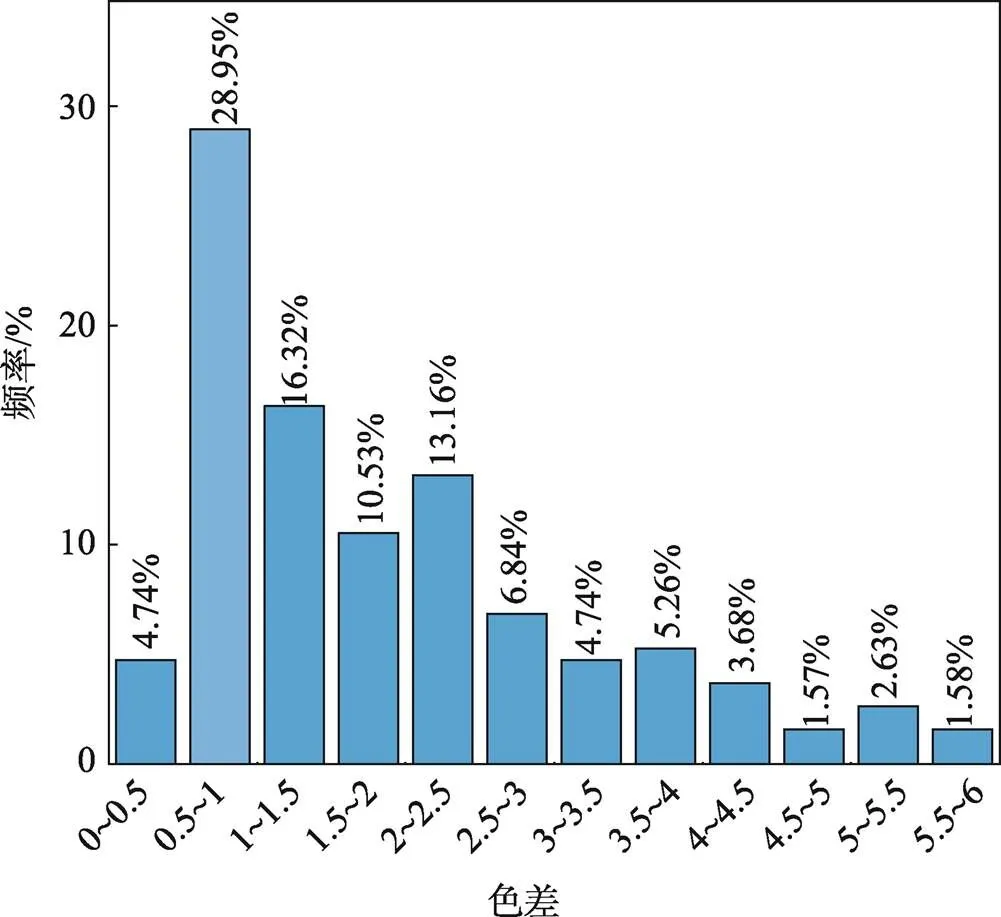
图4 样张色块色差频率分布

参考国际图形测量公司GMI的认证标准，其在专色色差方面认为，在测量背景为白色的前提下，印刷专色的颜色与标准色的误差小于2即为合格。从图4中可得，190个色块中73.7%的色块色差小于2.5，大多数色块色差均处于0～2内，占总频率的60.54%，整体平均色差为1.92 。说明本文所建模型具有较高精度，能基本满足凹印专色叠印颜色预测需求。

3 结语

本文针对凹印专色叠印色预测，利用密度与光谱反射率的关系，建立了前景色、后景色以及叠印色三者的关系。基于此关系并结合相对密度，建立了基于密度叠加原理的凹版专色叠印光谱预测模型。利用该模型，在已知前景色、后景色光谱反射率的前提下可预测叠印色专色光谱反射率。通过实打样不同专色叠印样张，从光谱均方根误差、决定系数2以及颜色色差3个方面验证模型的可行性及准确性。验证结果表明，本文提出的专色叠印光谱预测模型具有较高预测精度。在已知前景色、后景色以及比例系数的前提下可实现对不同阶调专色互相叠印结果的颜色预测，为企业生产实践提供一定指导，也可为其他颜色预测模型提供新的思路。

[1] 方恩印, 杨晟炜, 顾萍. 胞元纽介堡模型颜色预测性能的影响因素分析[J]. 包装工程, 2021, 42(17): 189-196.

FANG E Y, YANG S W, GU P. Influencing Factors of Color Prediction of Cellular Neugebauer Model[J]. Packaging Engineering, 2021, 42(17): 189-196.

[2] 孙栗媛. 基于半色调实地修正的纽介堡方程分色模型研究及应用[D]. 西安: 陕西科技大学, 2019: 1-12.

SUN L Y. Research and Application of Color Separation Model of Neugeburg Equation Based on Halftone Field Correction[D]. Xi'an: Shaanxi University of Science & Technology, 2019: 1-12.

[3] WANG B Y, XU H S, LUO M R, et al. Maintaining Accuracy of Cellular Yule-Nielsen Spectral Neugebauer Models for Different Ink Cartridges Using Principal Component Analysis[J]. Journal of the Optical Society of America A, Optics, Image Science, and Vision, 2011, 28(7): 1429-1435.

[4] 梁静, 黄浩, 廉玉生, 等. 喷墨打印系统多光谱特征化正向模型的建立[J]. 光谱学与光谱分析, 2018, 38(4): 1213-1218.

LIANG J, HUANG H, LIAN Y S, et al. Study of the Multi-Spectral Characterization Model for Inkjet Printing System and Its Application[J]. Spectroscopy and Spectral Analysis, 2018, 38(4): 1213-1218.

[5] WU K M, INOUE K, HARA K. Neugebauer Models for Color Error Diffusion Halftoning[J]. Journal of Imaging, 2020, 6(4): 23.

[6] 许法强. 基于光谱的多色复制技术研究及实现[D]. 武汉: 武汉大学, 2013: 1-37.

XU F Q. Research and Implementation of Multi-Color Replication Technology Based on Spectrum[D]. Wuhan : Wuhan University, 2013: 1-37.

[7] 郭晋一. 基于光谱匹配法Neugebauer方程的彩色打印系统特征化模型研究[D]. 杭州: 浙江大学, 2011: 1-15.

GUO J Y. Study on Characteristic Model of Color Printing System Based on Neugebauer Equation of Spectral Matching Method[D]. Hangzhou: Zhejiang University, 2011: 1-15.

[8] 杨慧芳. 基于光谱的专色叠印预测模型研究[J]. 北京印刷学院学报, 2016, 24(2): 17-21.

YANG H F. Predicting the Colorimetry of Spot Color Overprints Using Spectral Methods[J]. Journal of Beijing Institute of Graphic Communication, 2016, 24(2): 17-21.

[9] VAN DE CAPELLE J P, MEIRESON B. Method and Device for Determining the Color Appearance of Color Overprints: US, 6483607[P]. 2002-11-19.

[10] DESHPANDE K, GREEN P. A Simplified Method of Predicting the Colorimetry of Spot Color Overprints[C]// Color and Imaging Conference: Color Science and Engineering Systems, Technologies, and Applications, 2010: 213-216.

[11] 海敬溥, 郭凌华, 戚瑜颖, 等. 基于密度的凹版专色梯尺光谱预测模型的研究[J]. 光谱学与光谱分析, 2023, 43(1): 31-36.

HAI J P, GUO L H, QI Y Y, et al. Research on the Spectral Prediction Model of Gravure Spot Color Scale Based on Density[J]. Spectroscopy and Spectral Analysis, 2023, 43(1): 31-36.

[12] 郑元林. 印刷品质量检测与控制技术[M]. 北京: 化学工业出版社, 2010: 7-17.

ZHENG Y L. Quality Detection and Control Technology of Printed Matter[M]. Beijing: Chemical Industry Press, 2010: 7-17.

[13] 刘浩学. 印刷色彩学[M]. 北京: 中国轻工业出版社, 2008.

LIU H X. Color Science and Technology[M]. Beijing: China Light Industry Press, 2008.

[14] SHAMEY R, CAO R, TOMASINO T, et al. Journal of the Optical Society of America A, 2014, 31(6): 1328-1336.

[15] MELGOSA M, ALMAN D H, GROSMAN M, et al. Color Research & Application, 2013, 38(6): 429-436.

[16] 董娜, 程鹏飞, 孟凡净, 等. 基于K-M理论的荧光油墨实地印刷品颜色预测模型[J]. 数字印刷, 2020(5): 76-81.

DONG N, CHENG P F, MENG F J, et al. Color Prediction Model of Fluorescence Printing Based on K-M Theory[J]. Digital Printing, 2020(5): 76-81.

[17] 吕伟, 牟竟晓. 基于Kubelka-Munk理论的颜色预测模型[J]. 印刷杂志, 2020(3): 51-55.

LYU W, MOU J X. Color Prediction Model Based on Kubelka-Munk Theory[J]. Printing Field, 2020(3): 51-55.

[18] 赵德方, 黄新国. 基于Kubelka-Munk理论的光谱配色算法研究[J]. 包装学报, 2017, 9(1): 46-52.

ZHAO D F, HUANG X G. Research of Spectral Color Matching Algorithm Based on Kubelka-Munk[J]. Packaging Journal, 2017, 9(1): 46-52.

Research and Application of Spectral Prediction Model of Gravure Spot Color Overprint Color Based on Density

ZHANG Yiyang1,2, GUO Linghua1,2, WU Chengyun1,2, HAI Jingpu1,2, WANG Rongxin1,2, CHEN Rui1,2

(1. College of Bioresources Chemical and Material Engineering, Shaanxi University of Science and Technology, Xi'an 710021, China; 2. Key Laboratory of Functional Printing and Transport Packaging of China National Light Industry, Xi'an 710021, China)

The work aims to establish a spectral prediction model of spot color overprint color based on the relationship between density and spectral reflectance. Firstly, the relationship between front and back scene density and spectral reflectance was built according to the density definition formula. Based on this, a calculation method of spectral reflectance of overprint color was constructed. Secondly, the model was optimized, and the spectral prediction model of spot color overprint color was established. 30 spot color overprint color samples were printed by gravure. Based on Malab, the prediction model was verified with color difference and fitting coefficient2. Finally, another batch of spot color overprint color samples were printed under the same process conditions, and the accuracy of the model was checked by color difference. The experimental results showed that under the same dot area rate, there was a strong correlation between different spot color overprint color and its corresponding front and back scene density, and the fitting coefficient2was greater than 0.9. In the accuracy test of the model, the color difference between the predicted value of the model and the measured value of the sample was between 0 and 2.5 CIE1976 for 73.7%, and the color difference between the majority of the color blocks was between 0 and 2 CIE1976, accounting for 60.54% of the total frequency. The overall average color difference was 1.92 CIE1976. Therefore, the model proposed has high prediction accuracy and can basically meet the demand for color prediction

spot color overprint; ink density; spectral reflectance; prediction model

TS801.3

A

1001-3563(2024)05-0247-07

10.19554/j.cnki.1001-3563.2024.05.030

2023-07-10

陕西省重点研发计划资助（2020GY-320）；陕西省西安市未央区科技计划项目（201825，201862）