改进樽海鞘算法求解带时间窗的应急选址路径问题

徐帆，马良，张惠珍，陈曦

改进樽海鞘算法求解带时间窗的应急选址路径问题

徐帆，马良，张惠珍*，陈曦

（上海理工大学 管理学院，上海 200093）

为使应急物资及时高效地送到灾区, 针对多目标应急选址−路径问题，在考虑灾区的时间窗及物资运输过程中道路安全的情况下，以最小化经济成本、最小化时间惩罚成本及最大化道路安全性为目标，构建多目标优化模型。同时，设计改进的樽海鞘算法求解问题，以验证模型的可行性和算法的有效性。根据模型的特征对樽海鞘算法进行改进，运用随机生成和贪心算法相结合的方式生成初始解，利用交叉算子和邻域搜索算子改进原始算法的位置更新操作，引入非支配排序遗传算法（NSGA-Ⅱ）的精英保留策略，以提高算法的性能。经过多个算例测试，该算法能快速获得一簇Pareto解，与基本樽海鞘算法进行对比后可知，改进后的算法性能更优越。对于灾后及时响应的应急选址路径问题，采用改进的樽海鞘算法具有一定优越性，并在多个目标权衡的情况下，可供决策者根据目标的偏好找到较满意的解，对于研究应急选址路径问题具有一定的参考价值。

选址−路径问题；应急物资；时间窗；改进樽海鞘算法

近年来，地震、洪涝等自然灾害突发事件频繁发生。根据中国应急管理部与自然资源部等部门核定公布的数据显示，2022年我国自然灾害以洪涝、干旱、地震为主，共计造成1.12亿人次受灾，直接经济损失高达2 386.5亿元（http://www.mem.gov.cn/）。在应急管理中，救援仓库的设施选址问题（Facility Location Problem，FLP）与车辆路径问题（Vehicle Routing Problem，VRP）是很重要的2个子问题，它们整合了战略和战术决策[1]。将这2个子问题的综合问题称为选址−路径问题（Location-Routing Problem, LRP）。

目前，有大批学者在应急物流选址−路径上进行了相关研究。Vahdani等[2]考虑了具有不同容量水平的配送中心和仓库位置，以及仓库的库存和路线的可靠性，构建了一个两阶段多目标的混合整数模型。Zhang等[3]建立了一个考虑出行时间、应急救援费用和二氧化碳排放的不确定性多目标应急响应选址规划模型，并将不确定性仿真与遗传算法结合对模型进行求解。Wei等[4]考虑时间窗和成本，建立了带时间窗的应急选址−路径多目标模型，并利用混合蚁群算法进行求解。Shen等[5]基于粒子群算法结合禁忌搜索的混合两阶段算法，求解了一种模糊低碳应急选址−路径问题。刘长石等[6]针对震后物资配送模糊选址−路径问题，设计了一种混合免疫遗传算法，以应对震后应急。

现有研究针对应急LRP问题重点考虑的是经济因素和时间因素，而实际情境中灾后设施与道路可能会遭到一定破坏，在山区等环境恶劣地区这些因素会对救援人员的生命造成威胁，因而应该考虑物资配送过程中的安全性。文中引入道路安全性系数，构建一个多目标带时间窗的灾后选址−路径模型。

由于LRP问题属于NP-hard问题[7]，精确算法在求解大规模LRP问题时其速度通常较缓慢，甚至无法求到一个可行解，采用智能优化算法可以在短时间内找到满意解[8]。樽海鞘算法（Salp Swarm Algorithm，SSA）[9]是根据樽海鞘在海洋中移动和觅食时的群体聚集行为提出的群智能优化算法，相较于遗传算法、蚁群算法等经典算法，SSA算法的参数较少，具有结构简单、收敛速度快、控制参数少等优点，自开发以来广泛应用于特征选择[10-11]、图像[12]、工程设计[13-14]等多个领域，但很少应用于应急物资调度领域内的选址−路径等离散型问题中。文中基于SSA算法求解所构建的多目标LRP问题模型，并根据LRP模型的特征对SSA算法进行改进。通过不同规模的算例测试对构建的模型和算法进行验证，并与基本樽海鞘优化算法（Salp Swarm Algorithm，SSA）的求解结果进行对比，以验证算法的可行性和有效性。该算法在得到帕累托前沿面的同时，可供决策者根据不同目标的重要性选择恰当的物资调度方案，对应急LRP领域具有一定的参考意义。

1 问题描述和模型建立

1.1 问题描述与模型假设

描述研究的LRP问题：给定个候选应急仓库和个需求点，从候选应急仓库中选择若干条设施开放，并规划配送物资的路径，求解目标为最小化总成本、最小化物资延时送达的时间惩罚成本和最大化物资运输过程中的道路安全性。针对模型做如下假设：候选应急仓库与需求点地理位置关系已知；物资到达时间已知；车辆行驶的路网状况已知；需求点的物资需求量已知；应急仓库到需求点及需求点两两之间均存在可通行路径；物资送达的时间应越早越好，因此每个需求点的时间窗为半时间窗，晚到则会产生相应的时间惩罚成本。

1.2 符号与变量

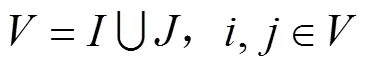
1.3 模型建立

目标函数1表示最小化总成本，该成本由3个部分组成：救援仓库开放所带来的固定成本、启用车辆的固定成本和应急物资的运输成本，见式（1）。目标函数2表示最小化车辆延时送达的时间惩罚成本，见式（2）。目标函数3表示最大化车辆行驶的道路安全性，见式（3）。这3个目标函数旨在从成本、时间和安全性3个维度来优化物流配送，实现在满足服务要求的同时，达到成本效益最大化和安全风险最小化的目标。约束条件1表示只有开放的救援仓库才能运输物资，见式（4）。约束条件2表示每个需求点有且仅有1辆车对其服务，见式（5）。约束条件3表示每个需求点有且仅有1个救援仓库对其进行服务，见式（6）。约束条件4表示救援仓库之间未连通，见式（7）。约束条件5表示救援仓库容量限制，即任意一个救援仓库发出去的物资不超过仓库的存储容量，见式（8）。约束条件6表示车辆容量约束，即每条配送路线的每辆车的负载低于车容量，见式（9）。约束条件7表示节点的车辆进出流量守恒约束，见式（10）。约束条件8表示消除子回路，见式（11）。约束条件9表示车辆在访问需求点时违反的时间窗长度，见式（12）。约束条件10表示时间窗口约束，见式（13）。约束条件11～14定义了决策变量及参数，见式（14）～（17）。

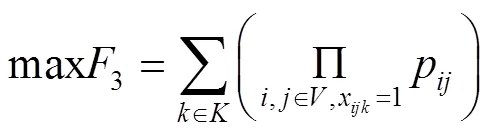
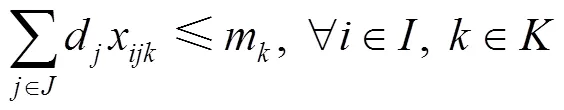
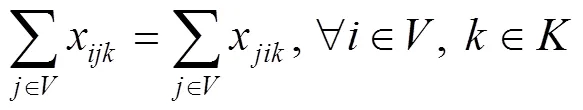
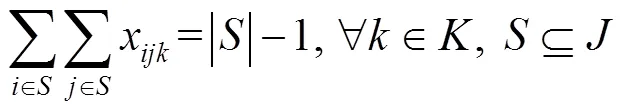
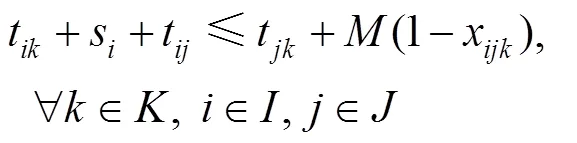
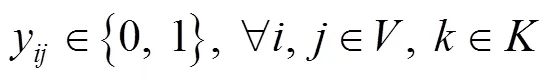
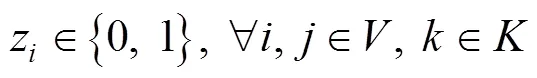
2 求解多目标LRP问题的改进樽海鞘优化算法

樽海鞘算法（Salp Swarm Algorithm，SSA）是一种受樽海鞘群体运动和觅食行为启发的基于群智能的优化算法。在樽海鞘群中，前一半个体为领导者，其余的为追随者，领导者引导种群，追随者互相跟随，所有个体形成一条“链”，通过樽海鞘个体的位置更新移动不断靠近食物源，最后快速准确地找到最优解[15]。此算法主要适用于连续优化问题，算法中樽海鞘的位置更新方法仅适用于连续空间的搜索。考虑到文中研究的问题属于离散优化问题，根据选址−路径问题的特点，并保有算法的特征，设计一种改进的樽海鞘算法。

2.1 解的表示

使用两段式的实数编码表示每个个体（可行解），所有需求点的数量为，染色体长度为2，解的构成由2个部分构成，分别为和，用不同的颜色表示，如图1所示。假设救援仓库、需求点的数量分别为4、8，解的编码长度为16，其中表示需求点与救援仓库的归属关系；表示需求点的初始配送顺序。如图1所示，4个候选救援仓库中2号救援仓库未开放，其中需求点4和7由救援仓库1提供服务，车辆配送物资的顺序为7→4；需求点5、1、6由救援仓库3提供服务，车辆配送物资的顺序为5→1→6。

同理，需求点2、3、8由救援仓库4提供服务，车辆配送物资的顺序为3→8→2。这种编码方式简单直观，可体现出开放的仓库、需求点的归属及救援仓库所服务的需求点的配送顺序。

图1 解的表示

2.2 初始种群的生成

初始解根据概率选择贪心算法或随机生成初始种群。其中，贪心算法只在生成需求点和仓库归属关系时发挥作用，首先计算出每个需求点到所有候选救援仓库的距离，按照升序排列，依照概率选择离自己最近或其他救援仓库。随机生成初始解时，首先随机为各个需求点分配救援仓库，确立需求点与救援仓库的归属关系，然后随机生成路径规划，确立每个救援仓库为需求点配送物资的顺序，计算见式（18）～（19）。

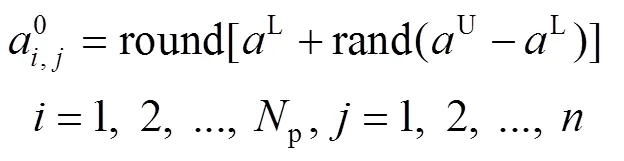
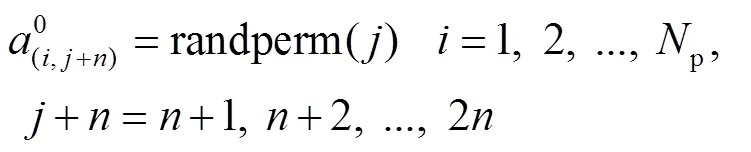
式中：U表示的上界；L表示的下界，最少有一个救援仓库为需求点提供配送服务，故L1；最多所有救援仓库都提供配送服务，故U为所有候选救援仓库的数量。初始解的长度为2，式（18）表示前列需求点与救援仓库的归属关系，式（19）表示+1列到2列需求点被配送的顺序。

2.3 快速非支配排序

在多目标问题中，由于多个目标之间往往存在冲突，很难找到一个解使所有目标函数最优，因此引入NSGA-Ⅱ中的非支配排序和拥挤度的概念[16]，按照每个个体的非支配和支配关系将他们排序分级，并且根据拥挤度选出同级别中的优解。拥挤度计算需要根据每个目标函数值按升序总体进行排序。然后，将等级中的边界解（具有最小和最大函数值的解）的拥挤度设为无穷大。中间解的拥挤度根据式（20）计算。

式中：为目标函数的数量；C为第个个体的拥挤度；1、–1为个体沿着帕累托边界的2个相邻个体；F()为个体的第个目标函数值。在所有个体中，排序值更靠前和拥挤度更大的个体更优。

2.4 领导者-跟随者自适应调整

在基本SSA算法中，领导者和追随者的数量始终各占种群总数的一半，这样导致在算法迭代早期，全局搜索的领导者比例过低，跟随者的比例过高，可能导致算法无法充分进行全局搜索而陷入局部最优解。在算法迭代后期，跟随者的数量过少，导致局部搜索不充分，会影响搜索的精度。

为了解决这个问题，这里引入了一种领导者−跟随者自适应调整策略。其中，樽海鞘领导者的数量会随着迭代次数的增加而自适应地减少，而跟随者的数量会自适应地增加。这样，算法在迭代早期可以保持强大的全局搜索能力，同时算法在迭代后期，其局部搜索能力逐渐增强，从而提高了整体的优化精度。

计算改进后的领导者−跟随者，每代中领导者数量等于p,跟随者数量等于(1–)p，p为种群数量，自适应权重因子的计算见式（21）。

式中：为当前迭代次数;max为最大迭代次数；init为控制参数的初始值；final为控制参数的终值。自适应权重因子在算法迭代中随着迭代次数而变化，由init、final确定。经过多次对比实验，最终将init取为0.7，将final取为0.3，用于动态控制算法初始时和结束时樽海鞘领导者和追随者的数量，更好地平衡算法的全局搜索和局部开发能力。

2.5 领导者位置更新

这里设计的改进领导者位置部分主要包含交叉操作Cross1、Cross2。交叉操作产生于领导者个体和食物源个体中，有利于平衡算法的全局搜索和局部搜索。食物源个体的选择：在排序值为1且拥挤度最大的个体中随机选择。Cross1为领导者个体与食物源个体部分的交叉，Cross2为领导者个体与食物源个体部分的交叉操作。具体操作如图2～3所示。

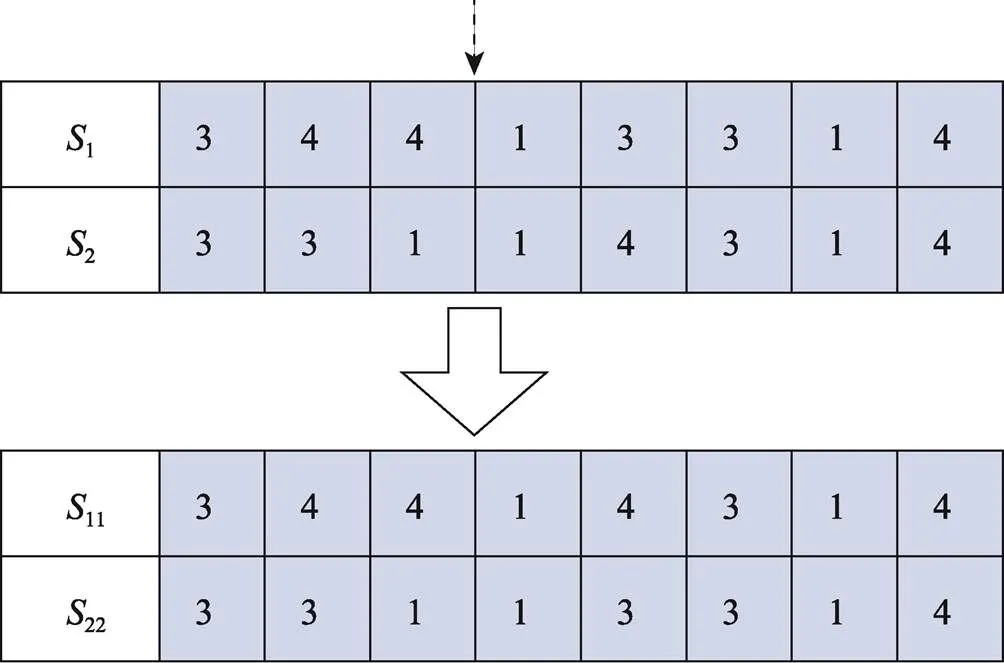
图2 Cross1操作演示

Cross1，如图2所示，1和2分别为领导者和食物源的部分，表示需求点和救援仓库的分配关系，随机生成的交叉点为3，将1和2点位3后的部分互换，交换彼此的需求点和救援仓库分配策略，得到子代11和22，新产生的子代个体不仅可以学习食物源个体的分配策略，也可能会产生更优质量的解。

Cross2，将领导者个体与食物源个体的部分进行交叉，部分表示配送顺序策略。如图3所示，1为领导者的部分，2为食物源的部分，作为2个父代，随机生成的交叉点为3、6，选择两点位之间的基因，在另一个父代上找到这些基因的位置，保持未选中的基因不变，按照选中的基因在另一父代上的出现顺序，交换2个父代个体中基因的位置，生成11、22。通过这种交叉方式可以学习到食物源个体的配送顺序策略，在增强种群多样性的同时也可能产生更优解。

图3 Cross2操作演示

将领导者个体和食物源个体的部分与部分进行交叉操作，并随机从子代[1111]或[2222]中选择一个作为新的领导者个体的位置。

2.6 追随者位置更新

对于追随者位置的更新，为了更好地对解进行局部开发，设计了交叉操作Cross3和邻域搜索，包括单点变异、两点交换、单点插入、逆转及仓库弃用。

1）交叉算子。在所有父代中随机选择1个樽海鞘个体，与当前追随者个体进行交叉。个体的部分和部分分别是2种不同的交叉方式，其中部分交叉与领导者位置更新时部分的交叉方式Cross1相同，部分的交叉方式Cross3具体操作如图4所示。

Cross3，追随者个体和父代樽海鞘个体的部分进行交叉，交叉后的个体可以学到父代个体的配送策略。交叉操作步骤：1为随机樽海鞘个体的部分，2为当前追随者的部分，作为2个父代，在1上随机生成的交叉点1，选择位置1上的元素1，其次找到2中位置1的元素2，再回到1中找到元素2所在的位置2，然后找到2中2位置上的元素3。重复之前操作，直到形成一个环，环中的所有元素的位置即是最后选中的位置。如图4所示，位置2→7→4→2形成一个循环，将1中相应位置的元素替换到2中，形成新的个体11。

图4 Cross3操作演示

2）邻域搜索。为了进一步提高樽海鞘算法在离散优化问题中的寻优能力，增强种群的多样性，结合LRP问题的特点选择5种邻域搜索机制对解进行局部开发，以相同的概率对解进行搜索。邻域搜索针对部分（需求点与仓库归属关系）和部分（需求点的配送顺序）进行搜索。针对部分有5种领域搜索操作，即单点变异、两点交换、插入、逆转、仓库弃用。针对部分有3种邻域搜索操作，即两点交换、插入、逆转。

单点变异：随机选取一个位置，将其对应的所属仓库进行变异操作。如图5所示，随机选中变异的位置是3，原本为4号仓库服务，标记为红色，随机生成新的1号仓库为需求点配送物资。

两点交换：随机选取位置和，将其对应的所属仓库的序号互换。如图6所示，随机选中的2个位置为3、6，标记为红色，将3号需求点和6号需求点所归属仓库互换，形成新的解。原来3号需求点由4号仓库服务，6号需求点由3号仓库服务，交换之后，3号需求点由3号仓库服务，6号需求点由4号仓库服务。

单点插入：随机选取部分的2个位置和，如图7所示，用红色标记。将位置的编码插到的编码之前，得到新的解。如图7所示，随机选中的位置为3和7，此时3到6号需求点所属仓库编码都向前移动，都发生了相应的改变。

逆转：随机选取部分的2个位置和然后将和之间（包括和）的所有序号逆向排序。如图8所示，选取的2个随机位置为3和7，将其中的序号[4 1 3 3 1]进行逆向排序，得到新的解。

仓库弃用：在开放的仓库索引里随机选择一个弃用仓库索引，并将其换成任意合理的仓库索引。具体操作如图9所示，选中的弃用仓库索引为4，关闭4号仓库，开放2号仓库，得到新的解。

同理，对于部分有3种搜索操作，操作步骤与相似，针对部分的操作改变了需求点的顺序，针对不同部分有不同的领域操作，在增强种群多样性的同时，也可能产生更优解。

图5 单点变异

图6 两点交换

图7 单点插入

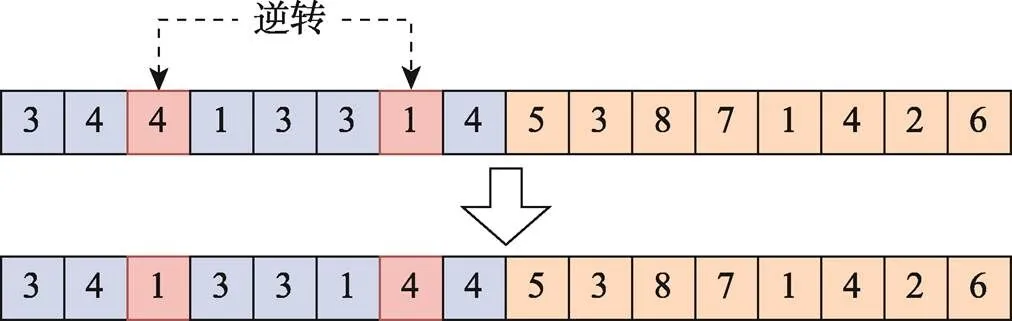
图8 逆转

图9 仓库弃用

2.7 精英保留机制

在ISSA算法中引入NSGA-Ⅱ的精英保留策略。将位置更新前的父代种群与位置更新后的子代种群合并为一个新种群，然后采用2.3节的方法，重新计算新种群的非支配排序等级和拥挤度，选取前p（种群数量）个最优的个体为下一代樽海鞘种群。精英保留机制有利于保留种群中的优良个体，提高种群的整体进化水平。

2.8 算法步骤

这里提出的改进多目标樽海鞘算法步骤如下。

1）初始化算法参数，种群规模p、算法最大迭代次数max，樽海鞘个体长度。

2）种群初始化，采用贪心算法与随机生成的方式生成p个樽海鞘个体作为初始可行解。

3）对种群进行非支配排序和拥挤度的计算，评估每个个体的目标函数值，并给每个个体排序。根据排序确定领导者和追随者。分配领导者和追随者种群，根据式（21）更新，前p个的樽海鞘个体为领导者，剩余个体为追随者。

4）确定食物源个体，在排序值最低且拥挤度最大的个体中随机选择一个作为食物源个体。

5）根据2.5节的策略更新领导者位置，根据2.6节的策略更新追随者位置。

6）精英保留机制将更新后的种群与父代种群合为一个大种群，并对其进行非支配排序，根据排序值选择前p个为新的种群。

7）判断迭代次数是否达到最大迭代次数max，如果达到，算法终止，如果未达到则返回步骤3），循环操作直到达到终止条件。

3 算例分析

采用Matlab 2016b，算法运行环境采用AMD Ryzen 5 5600H 处理器、3.30 GHz、内存16.0 GB、64位Windows 10操作系统。为了测试所提算法的性能，使用改进后的标准算例库中的部分算例及根据实际情景生成的一组算例进行求解，并对结果进行分析。

3.1 实验设计

借鉴Prins等[17]提出的标准LRP算例数据，所有参数均无量纲。由于算例库中无时间窗及道路安全性的相关数据，不完全适合于文中的问题。为了模拟真实情景，对算例中不同规模的部分数据进行适当改进后，生成文中的数据集。在生成的数据集中，车容量在{70, 150}之间，仓库容量在{300, 1 000}之间。其中，20-5-1的软时间窗最晚到达时间在[50, 300]之间生成，20-5-1b在[100, 400]之间生成，其余算例在[250, 500]之间生成。救援仓库需要在突发灾害后短时间内开放，需要耗费很多的人力、物力，因此将仓库的开放成本设置较高，设置为8 000，将救援车辆的启用成本设置为1 000，单位运输成本设置为100。同时将违反时间窗口的惩罚值设置为相对较高的1 000，每个点之间的道路安全性参数在(0, 1)之间随机生成。测试算例的相关信息如表1所示。

表1 测试算例相关信息

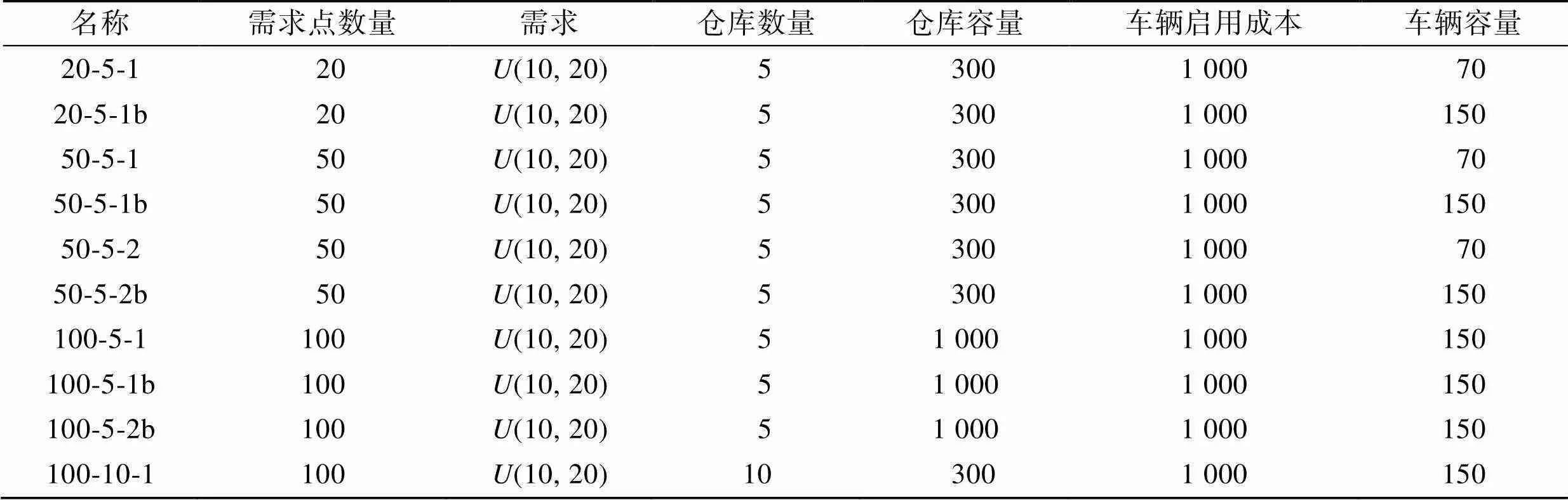
Tab.1 Relative data of test examples

3.2 参数设置

设置改进多目标樽海鞘算法的相关参数，每个个体的长度=2，表示需求点的数量。为了准确评估各个参数对ISSA算法性能的影响，这里采用参数调优策略。通过大量实验，根据算法迭代效果设置max=300。以下主要对种群规模p进行分析。为了测试种群规模p对算法性能的影响，利用算例20-5-1、50-5-1b进行实验对比。在保持其他参数恒定的情况下，设置种群为0.5、、1.5、2、2.5、3（为算例中的需求点数量），将实验运行20次，取帕累托前沿所有非支配解的平均值。

3.3 算例结果分析

对于每个算例，采用改进樽海鞘算法（ISSA）和原始樽海鞘优化（SSA）算法都运行20次，计算所有非支配解的经济成本（1）、时间成本（2）、道路安全性（3）的平均值，并找出所有非支配解中的最优解，结果见表3。此外，以50-5-1b为例，给出ISSA和SSA求解的三维帕累托前沿图，结果如图10所示。

由表3可知，ISSA算法在各算例中求解的1、2、3的最优值和平均值均优于SSA算法。从图10可以很清晰地看出，ISSA求出的帕累托最优解数量更多，并且帕累托面位于SSA求解出的帕累托面上方，说明改进后樽海鞘算法的性能更加优越，能得到更满意的解。

表2 种群数量p对解的影响

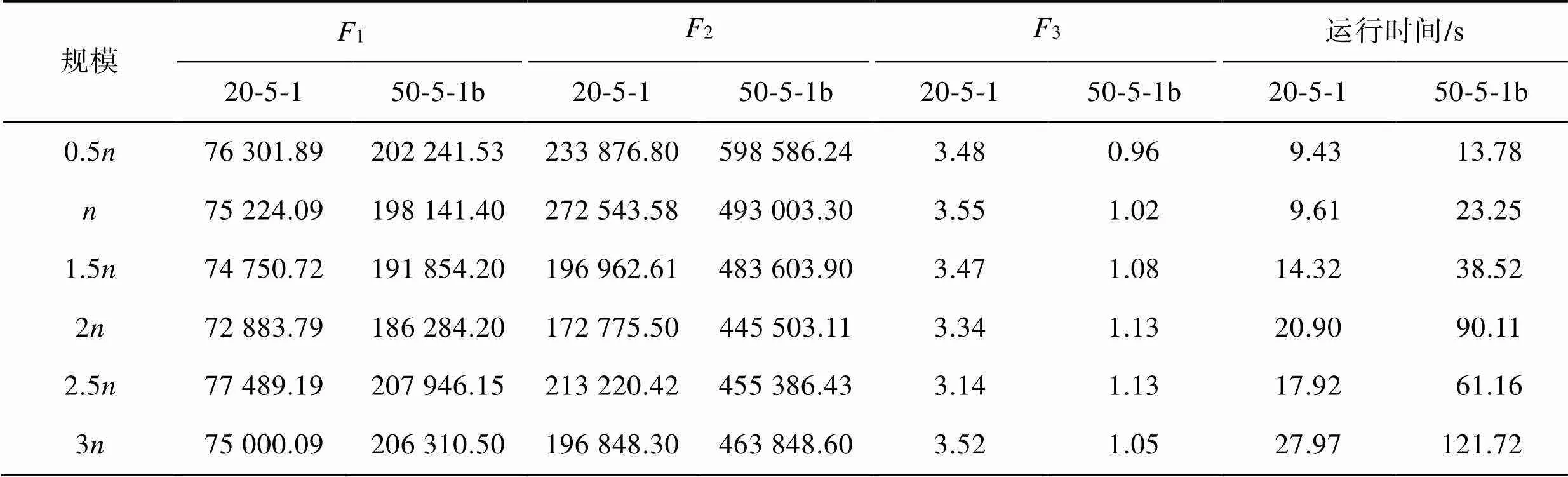
Tab.2 Effect of parameter Np on solution

表3 算法结果对比

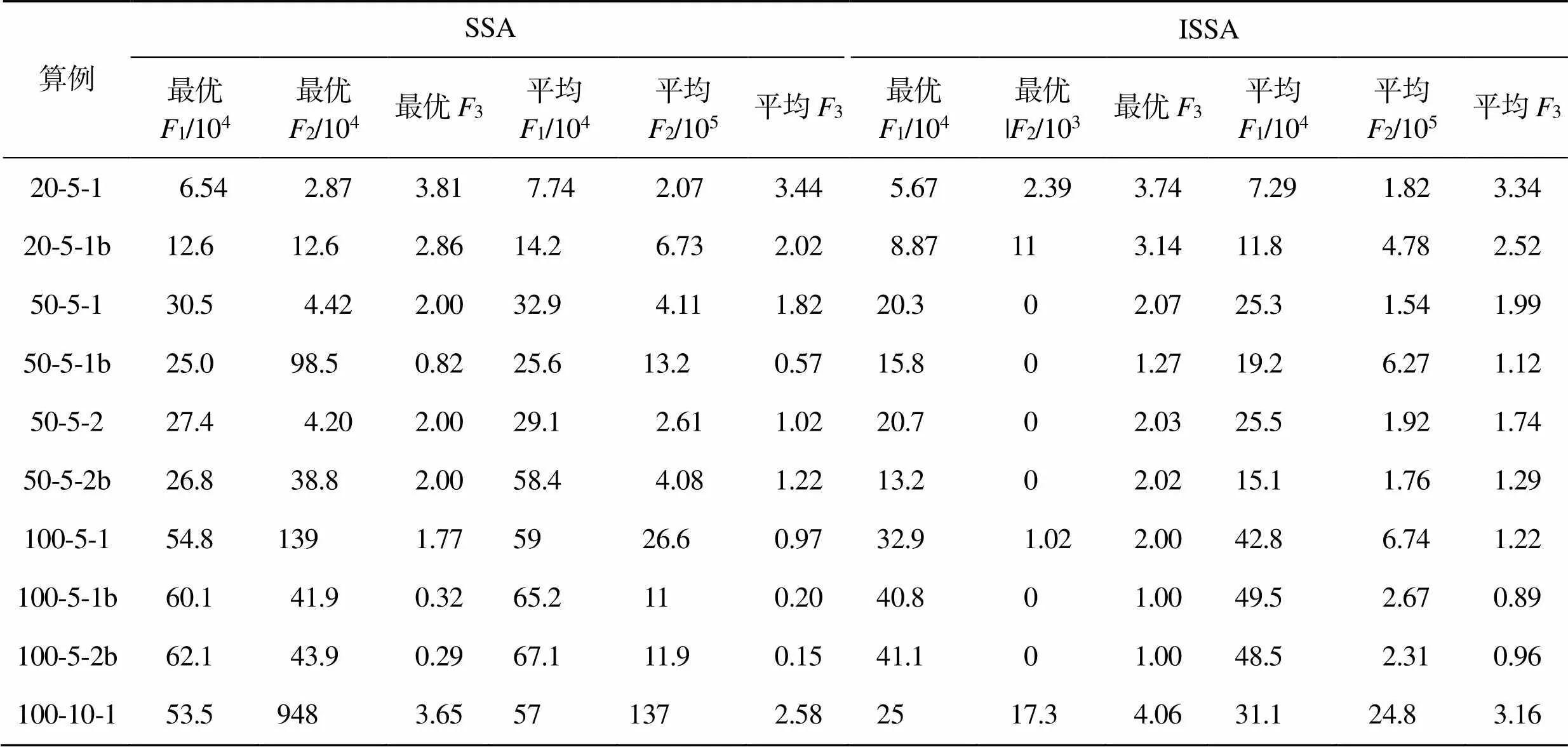
Tab.3 Comparison of algorithm results

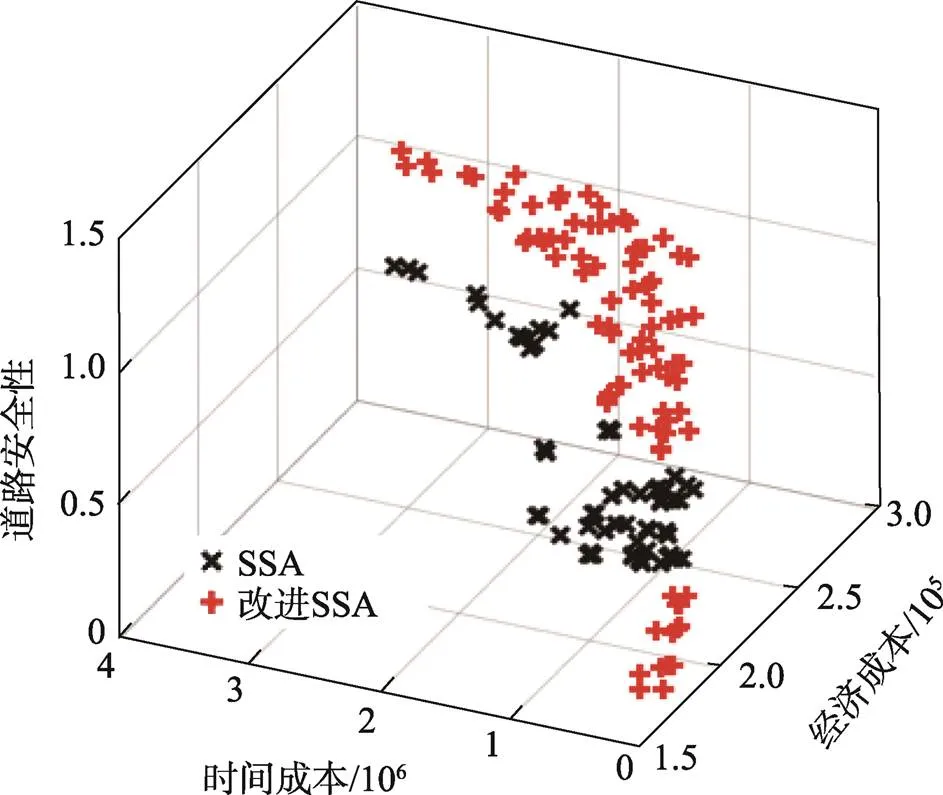
图10 ISSA和SSA求解的Pareto Optimal Surface (50-5-1b)

3.4 仿真实验分析

为了进一步验证文中模型和ISSA算法的有效性，选取上海市进行模拟实验，从上海市的地图中选取25个医院作为需求点，以火车站和机场作为候选仓库点。在选取这些点时，综合考虑了需求点的地理位置和紧急需求等因素。候选仓库点和需求点的具体信息见表4、5。需求点与候选仓库点之间的距离根据经纬度坐标计算得到。两点之间的距离根据式（22）计算。

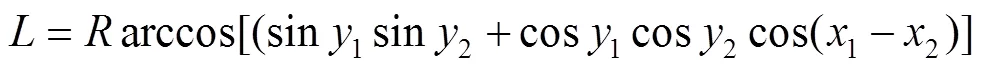
表4 候选仓库坐标

Tab.4 Candidate depot coordinates

为了验证算法及算法各个步骤的有效性，将未引入领导者−追随者自适应权重因子、未加入邻域搜索及未采用精英保留机制的算法记为ISSA-Ⅰ、ISSA-Ⅱ、ISSA-Ⅲ，将其运行10次，将它产生的最佳目标值（best）和最佳目标值的平均值（mean）与文中提出的ISSA算法结果进行对比，见表6。可以看出，算法求得的经济成本、时间成本及道路安全性都存在明显差距，这是由路径规划不同所致。从各个算法求得的平均值来看，采用ISSA算法求得的经济成本、时间成本及道路安全性都优于其他算法，说明在进行一系列改进后，在一定程度上提高了算法的寻优能力。

表5 需求点信息

Tab.5 Information of demand point

表6 算法改进对比

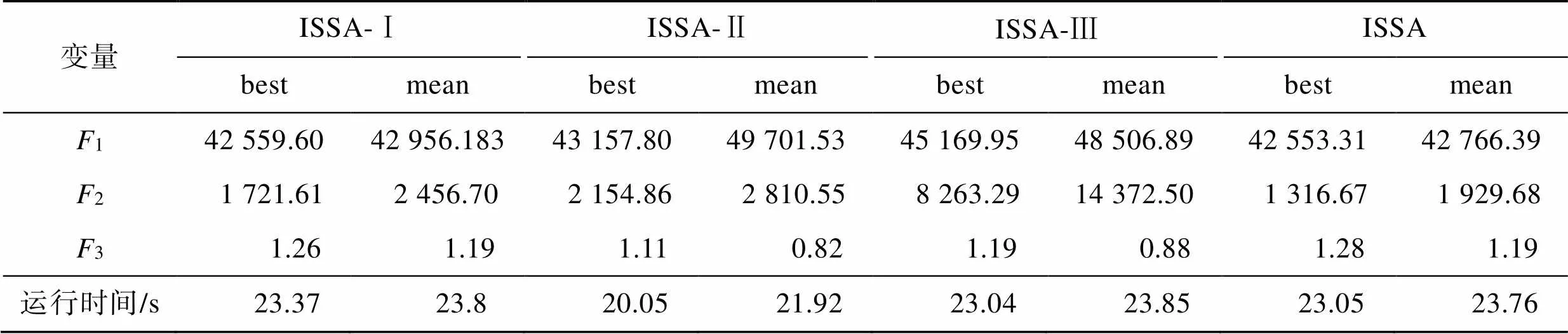
Tab.6 Algorithm improvement comparison

表7 具有代表性的有效解（=4,=25）

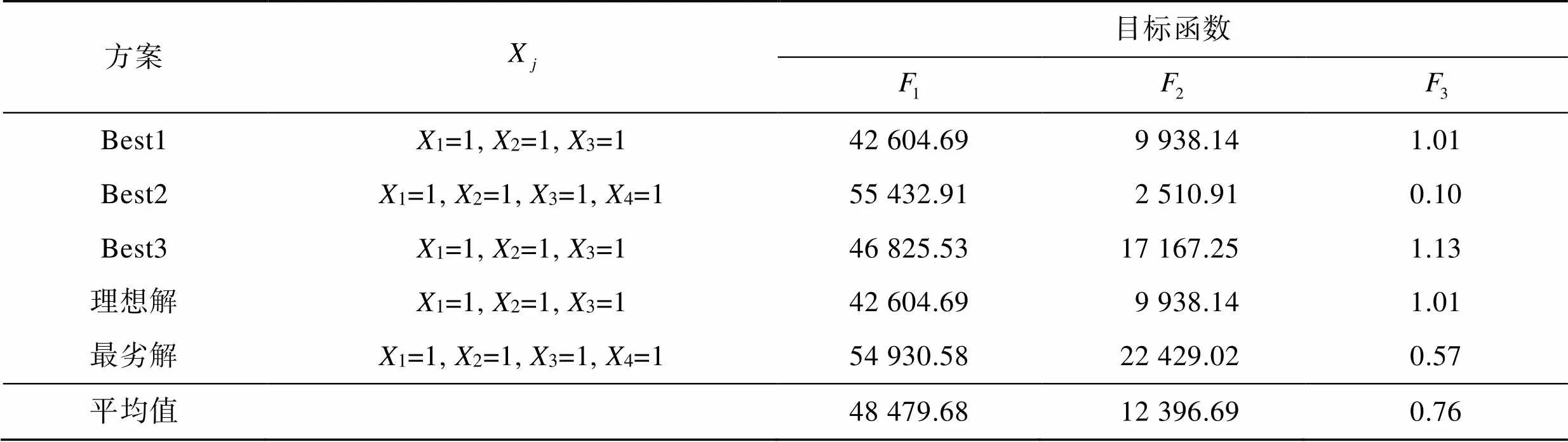
Tab.7 Representative valid solutions (m=4, n=25)

表8 理想解的路径规划

Tab.8 Route planning for the ideal solution

4 结论

针对突发灾害后的应急物资选址−路径问题进行了研究，为了达到配送物资的经济性、时效性及运输过程中的安全性，建立了一个在灾后及时响应的环境下具有时间窗口的多目标选址−路径模型，以经济成本最小化、时间惩罚成本最小化及道路安全性最大化为目标，为决策救援仓库选址及救援车辆的配送路线提供方案。为了有效解决多目标优化问题，根据LRP模型的特点及基本樽海鞘算法（SSA）的搜索机制提出了一种改进的樽海鞘算法（ISSA），并与未改进的基本樽海鞘算法进行对比。基于多个算例的分析比较，证实了文中所提模型和算法的科学性和有效性，在求解质量上具有一定的优越性。最后将ISSA用于实际背景下的算例中，验证了算法的有效性。同时，在权衡多个目标的状况下，提供了一种方案可供决策者找到较满意的解。

此研究也存在一些不足，如只考虑了确定性方案，而现实中信息的滞后性会导致很多信息不确定。后续会进一步考虑不确定情况对结果的影响，更加全面地考虑灾后物资调度的规划与决策。

[1] ZHONG S P, CHENG R, JIANG Y, et al. Risk-Averse Optimization of Disaster Relief Facility Location and Vehicle Routing under Stochastic Demand[J]. Transportation Research Part E: Logistics and Transportation Review, 2020, 141: 102015.

[2] VAHDANI B, VEYSMORADI D, NOORI F, et al. Two-Stage Multi-Objective Location-Routing-Inventory Model for Humanitarian Logistics Network Design under Uncertainty[J]. International Journal of Disaster Risk Reduction, 2018, 27: 290-306.

[3] ZHANG B, LI H, LI S G, et al. Sustainable Multi-Depot Emergency Facilities Location-Routing Problem with Uncertain Information[J]. Applied Mathematics and Computation, 2018, 333: 506-520.

[4] WEI X W, QIU H X, WANG D J, et al. An Integrated Location-Routing Problem with Post-Disaster Relief Distribution[J]. Computers & Industrial Engineering, 2020, 147: 106632.

[5] SHEN L, TAO F M, SHI Y H, et al. Optimization of Location-Routing Problem in Emergency Logistics Considering Carbon Emissions[J]. International Journal of Environmental Research and Public Health, 2019, 16(16): 2982.

[6] 刘长石, 彭怡, 寇纲. 震后应急物资配送的模糊定位-路径问题研究[J]. 中国管理科学, 2016, 24(5): 111-118.

LIU C S, PENG Y, KOU G. Research on Fuzzy Location-Routing Problem in Post-Earthquake Delivery of Relief Materials[J]. Chinese Journal of Management Science, 2016, 24(5): 111-118.

[7] PRODHON C, PRINS C. A Survey of Recent Research on Location-Routing Problems[J]. European Journal of Operational Research, 2014, 238(1): 1-17.

[8] LIU B J, ZHU L, REN J L. Intelligent Optimization Algorithm Grid Computing-Based Applications[J]. Journal of Intelligent & Fuzzy Systems, 2020, 39(4): 5201-5211.

[9] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems[J]. Advances in Engineering Software, 2017, 114: 163-191.

[10] 张达敏, 陈忠云, 辛梓芸, 等. 基于疯狂自适应的樽海鞘群算法[J]. 控制与决策, 2020, 35(9): 2112-2120.

ZHANG D M, CHEN Z Y, XIN Z Y, et al. Salp Swarm Algorithm Based on Craziness and Adaptive[J]. Control and Decision, 2020, 35(9): 2112-2120.

[11] ALJARAH I, HABIB M, FARIS H, et al. A Dynamic Locality Multi-Objective Salp Swarm Algorithm for Feature Selection[J]. Computers & Industrial Engineering, 2020, 147: 106628.

[12] 李志杰, 王力, 张习恒. 改进樽海鞘群优化K-means算法的图像分割[J]. 包装工程, 2022, 43(9): 207-216.

LI Z J, WANG L, ZHANG X H. Improved Salp Swarm Optimization K-Means Algorithm for Image Segmentation[J]. Packaging Engineering, 2022, 43(9): 207-216.

[13] SALGOTRA R, SINGH U, SINGH S, et al. Self-Adaptive Salp Swarm Algorithm for Engineering Optimization Problems[J]. Applied Mathematical Modelling, 2021, 89: 188-207.

[14] NAUTIYAL B, PRAKASH R, VIMAL V, et al. Improved Salp Swarm Algorithm with Mutation Schemes for Solving Global Optimization and Engineering Problems[J]. Engineering with Computers, 2022, 38(5): 3927-3949.

[15] ZHANG H L, CAI Z N, YE X J, et al. A Multi-Strategy Enhanced Salp Swarm Algorithm for Global Optimization[J]. Engineering with Computers, 2022, 38(2): 1177-1203.

[16] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[17] PRINS C, PRODHON C, CALVO R W. Solving the Capacitated Location-Routing Problem by a GRASP Complemented by a Learning Process and a Path Relinking[J]. 4OR, 2006, 4(3): 221-238.

Improved Salp Swarm Algorithm for Solving Multi-objective Emergency Location Routing Problem with Time Windows

XU Fan,MA Liang,ZHANG Huizhen*,CHEN Xi

(School of Management, University of Shanghai for Science & Technology, Shanghai 200093, China)

In order to ensure timely and efficient delivery of emergency resources to disaster areas, the work aims to construct a multi-objective optimization model for the multi-objective emergency location routing problem by taking into account the time windows of the disaster area and road safety during resources transportation, with the objectives of minimizing economic costs, time penalty costs, and maximizing road safety. At the same time, an improved salp swarm algorithm is designed to solve the problem, in order to verify the feasibility of the model and the effectiveness of the algorithm. Based on the characteristics of the model, the algorithm was improved by combining random generation and greedy algorithm to generate initial solutions. The position update operation of the original algorithm was improved by crossover operators and neighborhood search operators. The elite retention strategy of NSGA-Ⅱ was introduced to improve the performance of the algorithm. After test of multiple examples, this algorithm could quickly obtain a cluster of Pareto solutions and was compared with the original salp swarm algorithm. The improved algorithm had better performance. For the emergency location routing problem of timely response after a disaster, the improved salp swarm algorithm has certain advantages, and can provide decision-makers with satisfactory solutions based on the preferences of multiple objectives. It has a certain reference value for the field of emergency location routing problems.

location routing problem; emergency resources; time windows; improved salp swarm algorithm

TP301.6；TB485.3

A

1001-3563(2024)05-0220-10

10.19554/j.cnki.1001-3563.2024.05.027

2023-05-11

国家自然科学基金（72101149）；教育部人文社会科学基金（21YJC630087）；国家外国专家项目（G2023013029）