基于双模态有限时间滑模的永磁同步电机抗扰动控制

张会林，王帅，张建平

基于双模态有限时间滑模的永磁同步电机抗扰动控制

张会林，王帅，张建平

（上海理工大学 机械工程学院，上海 200093）

解决包装机工作过程中，因永磁同步电机的动态响应慢和抗扰动能力弱导致包装机精度不高的问题。设计一种双模态有限时间滑模控制器，实现系统有限时间收敛。将双模态函数引入趋近律增益，不仅能实现“大误差大增益，小误差小增益”，而且趋近律增益切换为小增益的时间可调，从而使电机获得更快的响应速度和更小的抖振。同时，设计有限时间扰动观测器对扰动进行观测，并进行前馈补偿，以此来提高系统的抗扰性能。实验结果表明，文中方法相较于另外2种对照方法，可以使电机的动态响应分别提升27%、37%，控制性能分别提升40%、70%，相较于超螺旋扰动观测器，可以使电机的抗扰性能提升58%。所提控制策略可以明显提高系统的动态响应、控制性能、抗扰性能，使得永磁同步电机更符合包装机的要求。

永磁同步电机；动态响应；抗扰动；双模态有限时间滑模控制器；有限时间扰动观测器

近年来，随着人们生活水平的不断提高，包装行业迎来很好的发展机遇，同时也对包装产业提出了更高的要求。电机作为包装机的核心器件，其控制性能决定了包装机的精度和效率[1]，其中，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）凭借其结构简单、控制精度高等优点，广泛应用于包装领域。

传统的PMSM通常采用PI控制器进行调速，但是在产品加工过程中，电机常会遇到负载突变和频繁变速等问题，传统的PI控制器无法满足系统对响应速度、抗扰性能的要求。针对此问题，提出了众多非线性控制方式，如预测控制[2-4]、自适应控制[5]、滑模控制[6]等。其中，滑模控制凭借其快速的动态响应，以及对干扰有较强的鲁棒性等优点，获得了大量关注。针对滑模控制通常存在的抖振问题，文献[7]用饱和函数代替开关函数来保证PMSM控制的连续性，以此来减小抖振；文献[8]在双幂次趋近律的基础上引入切换函数，减小了系统抖振；文献[1]提出了一种新型趋近律，解决了滑模控制收敛速度与抖振相矛盾的问题。上述方法只能实现渐进收敛，为了实现跟踪误差有限时间收敛，文献[9]将终端滑模面应用于PMSM 控制中，加快了滑模控制的收敛速度，但是传统的终端滑模面始终存在奇异问题。随后，非奇异终端滑模面被提出[10]，文献[6]基于非奇异终端滑模面，提出了一种快速终端滑模控制方法，但仍然存在较大的抖振。

虽然滑模控制具有较强的鲁棒性，但是它往往需要一个大的滑模增益来抑制干扰。如果能将扰动观测出来，并进行前馈补偿，就能极大地削弱滑模控制的抖振。文献[11]提出了一种基于超螺旋扰动观测器的控制策略，提高了PMSM的稳定性。文献[12]将PMSM系统所有的未知项定义为总扰动，并通过扰动观测器对其进行观测。文献[13]提出一种基于改进型扩张状态观测器的控制策略，提高了PMSM的控制性能。文献[14]针对参数变化导致PMSM控制性能下降的问题，提出了一种超局部模型，并用扩展滑模扰动观测器观测超局部模型的未知项，提高了系统的抗扰性能。上述观测器只能实现渐进收敛，导致扰动不能被及时观测出来，从而降低了PMSM的控制性能。

为了使 PMSM 能够更好地适应包装行业的要求，文中将对PMSM 的响应速度、控制性能、抗扰性能进行优化。首先，基于转速环，提出一种双模态有限时间滑模控制器（Dual-mode Finite Time Sliding Mode Controller, DFTSMC），使系统实现有限时间收敛，并减小系统抖振。然后，针对外界扰动导致系统控制性能下降的问题，设计一种有限时间扰动观测器（Finite Time Disturbance Observer, FTDO），快速地将扰动观测出来，并将扰动补偿到速度控制器中，提高系统的抗扰性能。最后，通过实验验证所提控制方案的有效性。

1 PMSM数学模型

在表贴式PMSM中，电磁转矩和运动方程分别见式（1）、（2）。

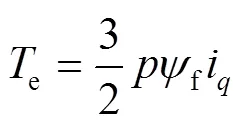
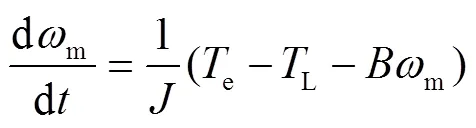
式中：为极对数；f为永磁体磁链；i为轴电流；m为电机的机械角速度；为转动惯量；为电磁转矩；e为电磁转矩；L为负载转矩。

PMSM的伺服系统通常由转速环和电流环组成的双闭环进行控制，其中转速环通常由PI控制器进行控制。文中拟设计一种新的转速环控制策略，以提高PMSM的动态响应、控制性能和抗扰动性能。

2 双模态有限时间滑模控制器设计

由于滑模控制拥有良好的动态响应和抗扰性能，故这里在PMSM的转速环中采用滑模控制。在传统的滑模控制中，由于采用线性滑模面，系统误差始终不能实现有限时间收敛，故文中设计了一种DFTSMC，以实现系统误差在有限时间内收敛到0，且能减小抖振。

在PMSM运行过程中，其控制性能易受到负载扰动、电气参数变化等的影响，这里将这些扰动量视为总扰动，并将其引入转速环控制器中，以减小实际运行中这些扰动量的影响，则式（2）可变为式（3）。

定义状态变量，见式（4）。

式中：ref为给定角速度。

为了保证系统跟踪误差可以在有限时间内收敛到0，避免滑模面存在奇异现象，选取非奇异终端滑模面[15]，见式（5）。

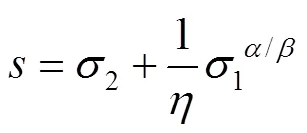
式中：1/为滑模面增益，且>0；>，、均为正奇数。

对式（5）求导，可得式（6）。

在传统的趋近律设计中，通常使用符号函数sign()作为切换函数，且趋近律增益为定增益。其中，符号函数的非连续性会导致系统发生抖振，趋近律增益决定了系统抖振的程度和滑模控制的收敛速度，它们之间的关系通常为：趋近律增益越大，收敛速度越快，抖振越大；趋近律增益越小，收敛速度越慢，抖振越小。如何克服系统收敛速度与抖振之间的矛盾成为滑模控制的关键。为了解决这一矛盾，设计了一种双模态有限时间趋近律，并采用饱和函数sat()代替符号函数，实现控制的连续性，其具体形式见式（7）。

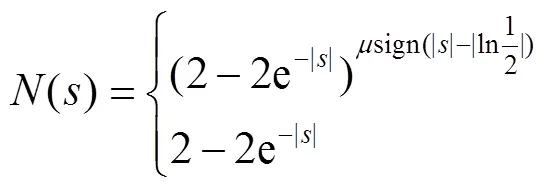
注1：将||>阶段，称为趋近模态；将||≤阶段，称为到达模态。在不同的模态采用不同的控制策略，这里将这种控制方式称为双模态控制。

定理1：式（7）所示的趋近律是稳定的。若把趋近律的增益设为1=2，则其收敛到滑模面的时间2的计算见式（8）。

选择李雅普诺夫函数，见（10）。

对式（10）求导，可得式（11）。

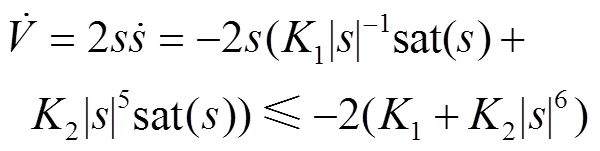
对式（12）做如下变化，见式（13）。

当1=2时，式（13）可化为式（14）。

式（14）两边同时积分，解得式（15）。

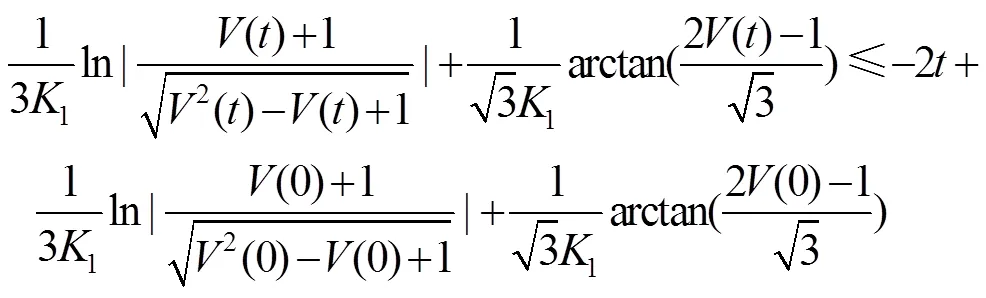
当=0时，=0，设在1时刻，系统状态收敛到滑模面上，此时存在式（16）。

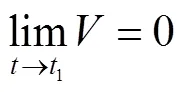
结合式（15）和式（16）可得式（17）。

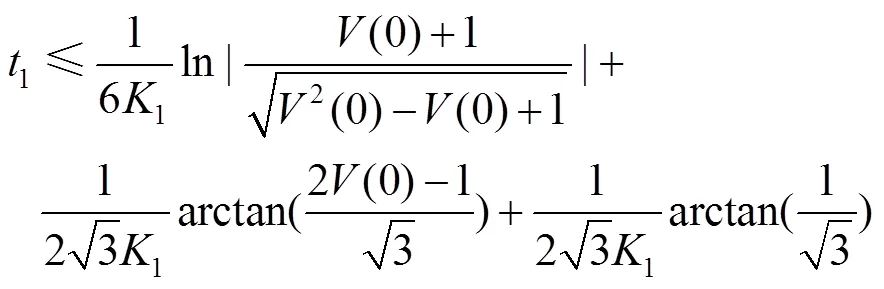
若采用式（9）所示的趋近律，系统状态收敛到滑模面的时间是有限的。为了描述方便，将采用此趋近律的控制器称为有限时间滑模控制器。

第2步，考虑()时，选取李雅普诺夫函数，见式（18）。

对式（18）求导，可得式（19）。

1）当系统状态远离滑模面时，这一阶段显然为趋近模态，此时存在式（20）。

在收敛速度上，显然双模态有限时间趋近律远远大于有限时间趋近律。

2）当系统状态接近滑模面时，此时存在2种模态：趋近模态、到达模态，分别见式（21）、（22）。

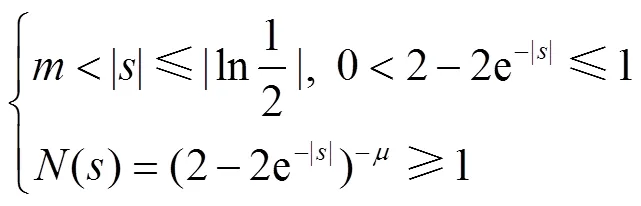
这一阶段，若系统为趋近模态，则双模态有限时间趋近律的收敛速度更快；在到达模态时，双模态有限时间趋近律的收敛速度较慢，但是此时系统状态距离滑模面很近。故总存在一个足够小的，使双模态有限时间趋近律的整体收敛速度更快，即2<1，定理1得证。

为了直观地对文中提出的双模态控制策略进行分析，通过Matlab绘制其波形，取为2，分别取为0.2、0.3，波形如图1所示。

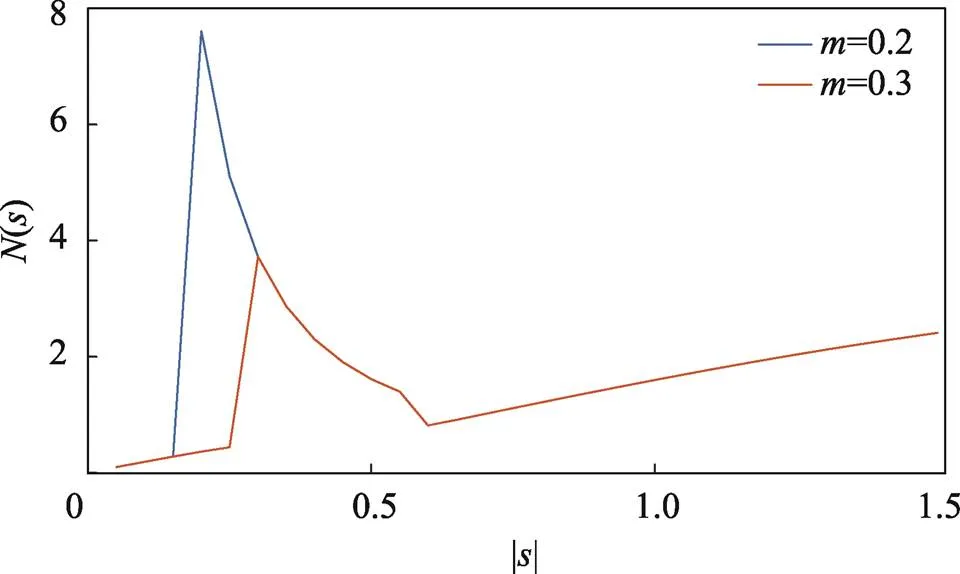
图1 函数波形

故这里选取双模态有限时间滑模控制器对电机转速环进行控制，结合式（3）、（4）、（6）、（7）可得轴电流的控制律，见式（23）。

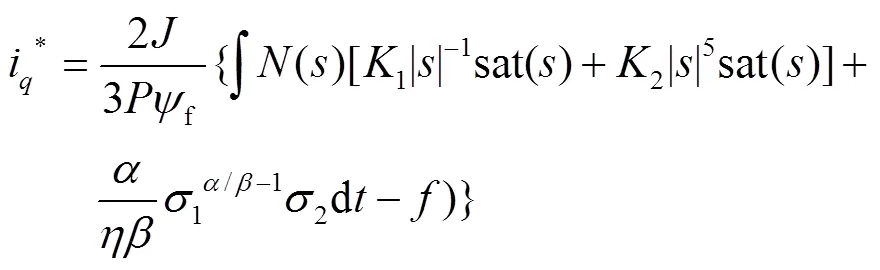
3 有限时间扰动观测器设计

由轴电流的控制律可以看出，其控制性能与总扰动有着较大关系。如果能够快速将总扰动观测出来，并补偿到系统中，就可提高系统的抗扰性能，故设计一种FTDO对其进行观测。由式（3）可得式（24）。

假设系统扰动变化缓慢，且存在上界，此时状态方程可表示为式（25）。

根据式（25），FTDO可以设计为如下形式，见式（26）。

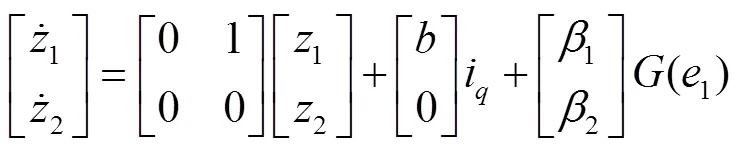
式中：1为m的估计值；2为总扰动的估计值；1、2为FTDO的增益；(1)为转速估计误差1的函数，且存在(0)=0。

用式（25）减去式（26），其观测误差可以表示为式（27）。

采用积分滑模面，见式（28）。

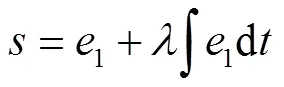
式中：为滑模面增益，且>0。

对式（28）求导，可得式（29）。

设计扰动观测器的目的：当系统受到扰动时，它可快速将扰动观测出来，并补偿到系统中，故其收敛速度越快越好。故设计了如下趋近律，见式（30）。

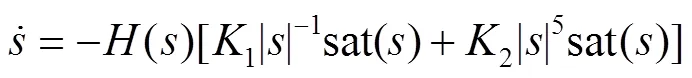
当系统状态收敛到滑模面后，由式（28）可得：当=0时，1=0。由式（29）得2=0，故该扰动观测器可在有限时间内观测出总扰动。结合式（27）、（29）、（30），可将控制律写为式（31）。

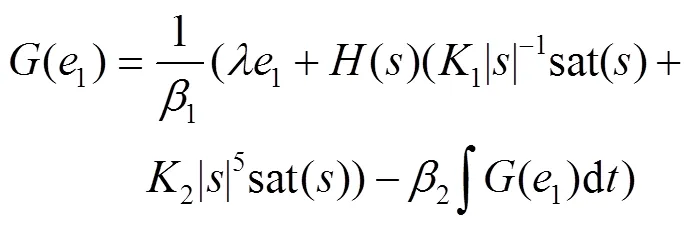
综上所述，结合式（23）可得扰动补偿后的轴电流的控制律，见式（32）。

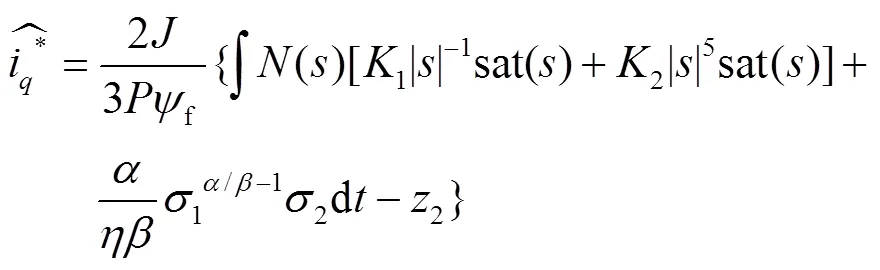
图2 基于文中所提方案的PMSM控制框图

4 实验验证

为了验证所提控制策略的有效性，搭建了实验平台对其进行验证，主控芯片选择沁恒公司的CH32V307VCT6芯片，采样频率设置为20 kHz。通过Matlab编写上位机对电机的转速和转矩进行监测，实验平台如图3所示。实验所用永磁同步电机的具体参数和控制器参数如表1所示。

图3 实验平台

表1 PMSM和控制器参数

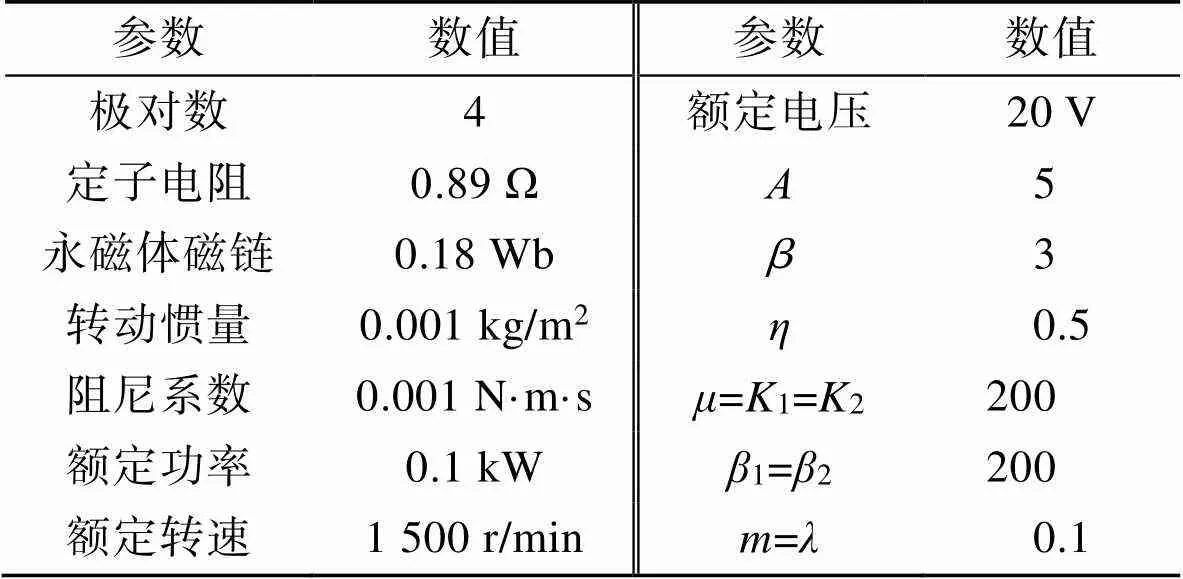
Tab.1 PMSM and controller parameters

这里通过变速实验验证其动态响应，通过加载实验验证其抗扰性能，通过连续加减载实验验证其在复杂工况下的有效性，通过转矩的波动范围验证其控制性能。

工况1：空载启动，变速运行。给定转速为500 r/min，空载启动，在2 s时转速给定突变为1 000 r/min，分别使用文中所提的DFTSMC、有限时间滑模控制器、快速终端滑模控制器[6]对电机转速进行控制。实验结果如图4、图5所示。

综上可以看出，DFTSMC相较于另外2种控制方式，其动态响应分别提升了27%、37%，控制性能分别提升了40%、70%，因此文中提出的DFTSMC可以在加快系统响应速度的同时提高系统的控制性能。

工况2：空载启动，突加负载。给定转速为1 000 r/min，空载启动，在2 s时突加0.6 N·m负载，分别使用文中提出的有限时间扰动观测器（FTDO）和超螺旋扰动观测器[11]（Super-Twisting Disturbance Observer, STDO）对扰动进行观测，并进行前馈补偿。实验结果如图6及图7所示。

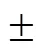
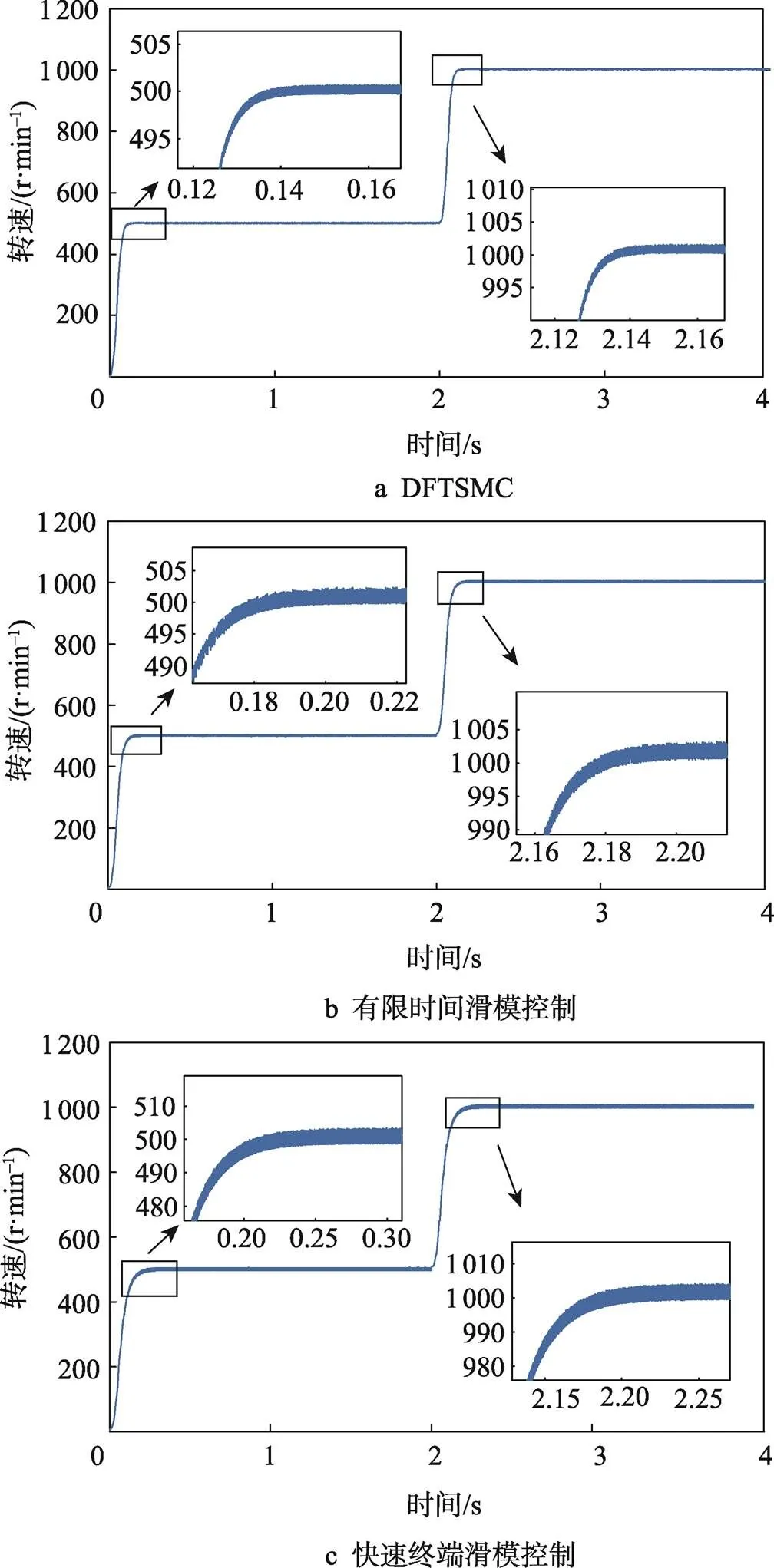
图4 转速对比

综上可以看出，采用FTDO时，抗扰性能提升了58%，控制性能提升了25%，故提出的FTDO表现出更好的抗扰动性能和控制性能。

工况3：带载启动，连续加减载。给定转速为1 000 r/min，带载启动，在1 s时突加0.3 N·m负载，在2、3 s时连续减载，分别使用文中提出的FTDO和STDO[13]对扰动进行观测，并进行前馈补偿。实验结果如图8～9所示。

由图8可以看出，当电机在连续加减载时，若采用DFTSMC+FTDO，在加载阶段，电机转速仅需0.02 s即可达到稳态，转速仅下降2 r/min，在减载阶段，电机转速仅需0.01 s即可达到稳态，且转速上升了1 r/min；若采用DFTSMC+STDO，在加载阶段，电机转速达到稳态需要0.03 s，且转速下降了3 r/min，在减载阶段，电机转速达到稳态需要0.015 s，且转速上升了1.5 r/min。

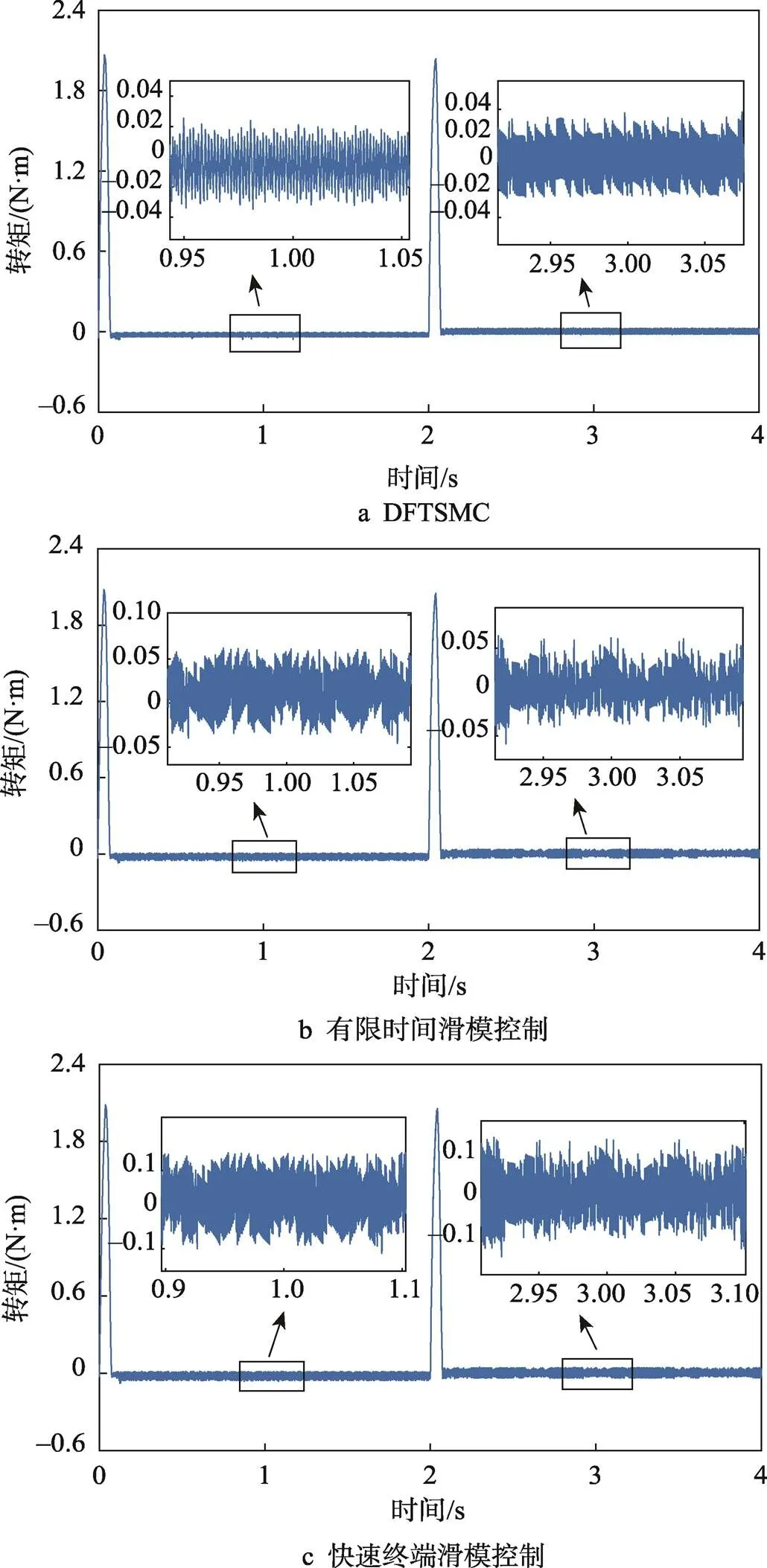
图5 转矩对比

综上可以看出，即使在面对复杂工况时，文中提出的控制策略仍然表现出优秀的控制能力。为了更直观地对上述实验结果进行对比，整理数据见表2。

图6 转速对比

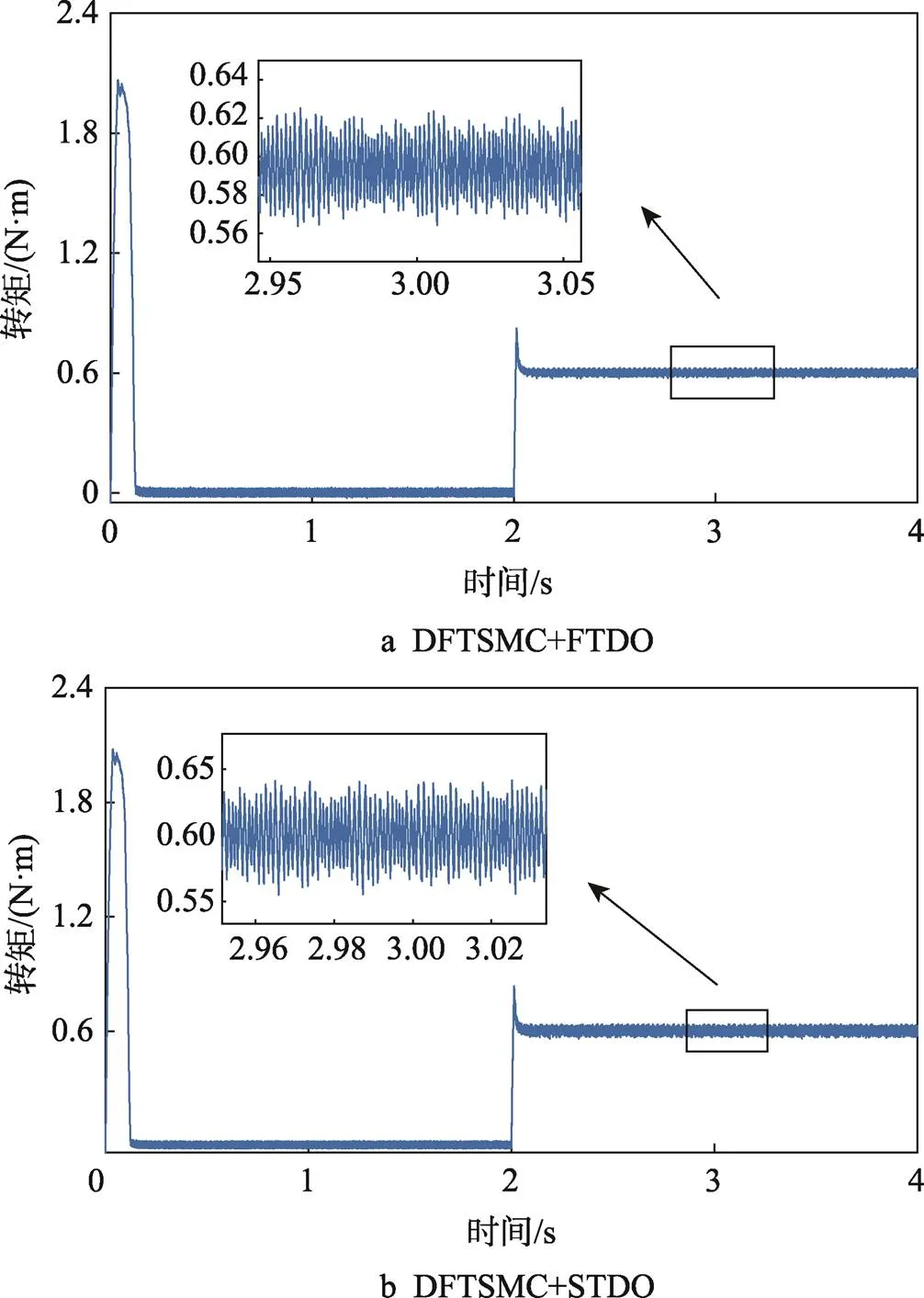
图7 转矩对比

图8 转速对比

图9 转矩对比

表2 实验结果对比

Tab.2 Comparison of experiment results

5 结语

为了提高PMSM的动态响应、抗扰性能，在转速环，设计一种DFTSMC，通过分析证明它可在加快系统收敛速度的同时，抑制滑模控制的抖振。针对永磁同步电机在运行过程中出现的扰动问题，将FTDO观测出的扰动前馈到转速环中，以提高系统的抗扰性能。最后，通过实验验证了文中所提方法的有效性，结果表明，所提方法可以明显提高系统的动态响应、控制性能和抗扰性能。

[1] 董洪昭, 杜秋月, 刘珂, 等. 基于新型趋近律的永磁同步电机动态性能优化[J]. 包装工程, 2023, 44(5): 163-170.

DONG H Z, DU Q Y, LIU K, et al. Dynamic Performance Optimization of Permanent Magnet Synchronous Motors Based on a New Approach Law[J]. Packaging Engineering, 2023, 44(5): 163-170.

[2] 鲍旭聪, 王晓琳, 顾聪, 等. 超高速永磁电机驱动系统电流环稳定性分析与改进设计[J]. 电工技术学报,2022, 37(10): 2469-2480.

BAO X C, WANG X L, GU C, et al. Stability Analysis and Improvement Design of Current Loop of Ultra-High-Speed Permanent Magnet Motor Drive System[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2469-2480.

[3] NIU F, CHEN X, HUANG S P, et al. Modelpredictive Current Control with Adaptive-Adjustingtimescales for PMSM[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 108-117.

[4] 张晓光, 闫康, 张文涵. 开绕组永磁同步电机混合双矢量模型预测控制[J]. 电工技术学报,2021, 36(1): 96-106.

ZHANG X G, YAN K, ZHANG W H. Hybrid Double Vector Model Predictive Control for Open Winding Permanent Magnet Synchronous Motor with Common DC Bus[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 96-106.

[5] 赵希梅, 王浩林, 朱文彬. 基于自适应模糊控制器和非线性扰动观测器的永磁直线同步电机反馈线性化控制.控制理论与应用, 2021,38(5): 595-602.

ZHAO X M, WANG H L, ZHU W B. Feedback Linearization Control of Permanent Magnet Linear Synchronous Motor Based on Adaptive Fuzzy Controller and Nonlinear Disturbance Observer[J]. Journal of Control Theory and Applications, 2021, 38(5): 595-602.

[6] 张智鑫, 刘旭东. 基于ESO的永磁同步电机伺服系统快速终端滑模控制[J]. 控制理论与应用, 2023, 40(7): 1233-1242.

ZHANG Z X, LIU X D. Fast Terminal Sliding Mode Control of Permanent Magnet Synchronous Motor Servo System Based on ESO[J]. Control Theory and Application, 2023, 40(7): 1233-1242.

[7] 孙杰, 崔巍, 范洪伟, 等. 基于改进滑模观测器的永磁同步电动机无位置传感器控制[J]. 微特电机, 2011, 39(2): 60-62.

SUN J, CUI W, FAN H W, et al. Vector Control for Permanent Magnet Synchronous Motors Based on Improved Sliding Mode Observer[J]. Small & Special Electrical Machines, 2011, 39(2): 60-62.

[8] 朱其新, 黄旭, 朱永红. 基于新型趋近律的永磁同步电机非奇异终端滑模控制[J]. 机床与液压, 2022, 50(23): 148-152.

ZHU Q X, HUANG X, ZHU Y H. Non Singular Terminal Sliding Mode Control of Permanent Magnet Synchronous Motor Based on a New Approach Law[J]. Machine Tools and Hydraulics, 2022, 50(23): 148-152.

[9] 李赓. 基于改进超螺旋算法的永磁同步电机速度控制研究[D]. 桂林: 桂林理工大学, 2020: 33-37.

LI G. Research on Speed Control of Permanent Magnet Synchronous Motor Based on Improved Super Helix Algorithm[D]. Guilin: Guilin University of Technology, 2020: 33-37.

[10] XU B, SHEN X, JI W, SHI G, et al. Adaptive Non-Singular Terminal Sliding Model Control for Permanent Magnet Synchronous Motor Based on Disturbance Observer. IEEE Access, 2018, 6(2): 48913-48920.

[11] 韩琨, 张长征, 袁雷. 基于超螺旋滑模扰动观测器的永磁同步电机无传感器抗干扰控制策略研究[J]. 包装工程, 2023, 44(3): 139-147.

HAN K, ZHANG C Z, YUAN L. Research on Sensorless Anti disturbance Control Strategy of Permanent Magnet Synchronous Motor Based on Super Spiral Sliding Mode Disturbance Observer[J]. Packaging Engineering, 2023, 44 (3): 139-147.

[12] CHEN J, YAO W, REN Y, et al. Nonlinear Adaptive Speed Control of a Permanent Magnet Synchronous Motor: a Perturbation Estimation Approach[J]. Control Engineering Practice, 2019, 85: 163-175.

[13] 赵峰, 罗雯, 高锋阳, 等. 考虑滑模抖振和扰动补偿的永磁同步电机改进滑模控制[J]. 西安交通大学学报, 2020, 54(6): 28-35.

ZHAO F, LUO W, GAO F Y, et al. An Improved Sliding Mode Control for PMSM Considering Sliding Mode Chattering and Disturbance Compensation[J]. Journal of Xi'an Jiaotong University, 2020, 54(6): 28-35.

[14] 赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2386.

ZHAO K H, DAI W K, ZHOU R R, et al. Novel Model-Free Sliding Mode Control of Permanent Magnet Synchronous Motor Based on Extended Sliding Mode Disturbance Observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2386.

[15] FENG Y, YU X H, MAN Z H. Non-Singular Terminal Sliding-Mode Control of Rigid Manipulator[J]. Automatic, 2002, 8(12): 2159-2167.

Disturbance Rejection Control of Permanent Magnet Synchronous Motor Based on Dual-mode Finite Time Sliding Mode

ZHANG Huilin,WANG Shuai,ZHANG Jianping

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to solve the problem of low precision in packaging machines in work due to the slow dynamic response and weak disturbance rejection ability of permanent magnet synchronous motors. A dual-mode finite time sliding mode controller was designed to realize finite time convergence of the system. By adding a dual-mode function to the reaching law, it could make the sliding mode gain achieve "large error and large gain, small error and small gain", and the time of the sliding mode gain switched to small gain was adjustable, so that the motor could achieve faster response speed and less chattering. At the same time, a finite time disturbance observer was designed to observe the disturbance, and feed-forward compensation was performed to improve the disturbances rejection performance of the motor. The experimental results showed that if the method proposed was used to control the motor, compared with the control groups, the dynamic response was improved by 27% and 37% and the control performance was improved by 40% and 70%. Compared with the super-spiral disturbance observer, the disturbance rejection performance of the motor was improved by 58%. Therefore, the control strategy proposed can significantly improve the dynamic response, control performance, and disturbance rejection ability of the system, which will let permanent magnet synchronous motor more suitable for the needs of packaging machines.

permanent magnet synchronous motor; dynamic response; disturbance rejection; dual-mode finite time sliding mode controller; finite time disturbance observer

TP13；TB486

A

1001-3563(2024)05-0188-09

10.19554/j.cnki.1001-3563.2024.05.023

2023-05-17

国家自然科学基金（12172228,11572187）；上海市自然科学基金（22ZR144400）