基于LESO的轮式移动机器人滑模轨迹跟踪控制

罗 淇，陈昌忠,2，刘 鑫

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000；2.人工智能四川省重点实验室，四川 宜宾 644000）

引言

轮式移动机器人(Wheeled Mobile Robot，WMR)因具有占地面积小、控制简单、机动灵活等优点被广泛应用于医疗、民用工程等领域[1-3]。为使WMR经预设路线到达指定地点，国内外学者利用了多种控制方法来设计WMR 轨迹跟踪控制器，如自抗扰控制[4]、滑模控制[5]、模型预测控制[6]、反步法[7]。然而，WMR 的工作路段可能存在路面湿滑、凹凸不平等情况而发生车轮打滑的情况，使机器人偏离预设轨迹[8-14]。因此，研究车轮打滑情况下的WMR 轨迹跟踪具有重要实际意义。

文献[8]引入滑动率表示左右轮的打滑程度，设计滑模观测器对打滑扰动进行估计。文献[9]研究Mecanum 轮打滑干扰的全向移动机器人轨迹跟踪，结合反步法运动学控制器和非线性误差反馈控制律设计了自抗扰反步控制器。文献[10]基于积分终端滑模控制设计了运动学模型下的WMR 侧滑扰动的轨迹跟踪控制。文献[11]利用非线性干扰观测器对机器人自身以及打滑集总干扰进行估计，设计了鲁棒跟踪控制器。文献[12]设计运动学控制器和自抗扰动力学控制器并证明了WMR 车轮打滑动力学模型是有界输入有界输出且稳定的。文献[13]设计WMR 的辅助运动学控制器，通过观测器估计和补偿干扰，使机器人实际速度收敛到辅助速度。文献[14]利用神经网络的方法对打滑干扰进行估计，设计了集合运动学模型的动力学控制器。然而，文献[8-10]仅分析机器人运动学模型，未考虑动力学模型，可能会使运动学控制器提供的虚拟速度与动力学控制器输出的实际速度存在偏差；文献[11]跟踪误差位于规定的范围，速度跟踪波动较大；文献[12-14]未进行扰动误差分析。

鉴于此，本文利用线性扩张状态观测器和积分滑模面设计轮式移动机器人车轮打滑情况下的轨迹跟踪控制方案。该方案由两部分组成，运动学控制器输出虚拟速度，动力学控制器输出力矩。在移动机器人打滑动力学模型下，将总扰动作为一个新的状态变量，利用线性扩张状态观测器对总扰动进行估计。基于实际速度与虚拟速度之间的跟踪误差设计带有积分项的滑模面，将总扰动的估计值前馈并结合积分滑模面设计动力学控制器。最后与基于超螺旋干扰观测器设计的轨迹跟踪控制方案进行仿真对比，验证所提出方案的有效性。

1 模型描述

WMR 系统模型是非完整约束的[1]，通常由运动学模型和动力学模型描述。

1.1 运动学模型

轮式移动机器人的运动模型如图1 所示，其中图1(a)表示未打滑情况，图1(b)表示打滑情况。图1(a)中，两后轮为驱动轮，前轮为随动轮，点p为两驱动轮轴线的中点，点po为移动机器人的质心点，定义两个坐标系用来描述WMR 的位姿和运动状态，其中XOY是以地面为参考系的全局坐标系，xo pyo是以机器人两驱动轮轴线的中点为原点的局部坐标系。2r为驱动轮直径，2b为两驱动轮之间的距离，d为机器人质心与驱动轮轴线中点的距离，υ为WMR行进的线速度，ω为机器人车体转动的角速度，θ为方向角即机器人运动方向与X轴方向的夹角，φR、φL分别表示右、左驱动轮旋转的角度。定义轮式移动机器人在全局坐标系中的位姿向量为q=[x,y,θ,φR,φL]T，其中(x,y)表示两驱动轮轴线中点p在全局坐标系的位置，(xc,yc)表示移动机器人质心点po在全局坐标系的位置。

图1 轮式移动机器人运动示意图

图1(b)中，μ为车轮打滑时对线速度的扰动量；ηL与ηR分别为车轮打滑时左右驱动轮旋转角速度的扰动量。当车轮受到打滑影响时，理想非完整约束条件会被破坏，因此新约束条件[11]的矩阵表达式为：

定义矩阵S(q) 为满足A(q) ·S(q)=0 解空间的一组基，则WMR打滑时的运动学模型[11]为：

1.2 动力学模型

由式(2)可知，当车轮在地面上发生打滑现象时，其速度会受到影响，因此引入动力学模型对车轮速度进行调整，WMR动能函数[7]表示为：

式中，mc为车体质量；Ic为WMR 车体绕经其质心点po点垂直轴的转动惯量；Iw为驱动轮绕轮轴的转动惯量。

由式(3)对位姿向量q=[x,y,θ,φR,φL]T中5 个元素分别求偏导并代入WMR 系统拉格朗日方程得到WMR动力学模型[7]为：

其中，M(q)∈ℝ5×5为WMR 系统的惯性矩阵；V(q,)∈ℝ5×5为科氏矩阵；B(q)∈ℝ5×2为输入变换矩阵；λ∈ℝ3×1为拉格朗日乘子向量；τ=[τR,τL]T为驱动轮力矩控制的输入向量。

对式(2)求导得¨，将式(2)和代入式(4)，并左乘ST(q)，可进一步得打滑动力学模型[12]为：

2 控制方案设计

WMR 轨迹跟踪控制方案结构框图如图2 所示。运动学控制器以WMR 产生的实际位姿与期望位姿之差即位姿误差和期望速度作为输入，输出为虚拟控制速度zc[14]。LESO 通过控制量和输出量估计系统状态，并对系统受到的总扰动进行估计。动力学控制器以实际速度和虚拟速度之差即速度跟踪误差ze和总扰动的估计值作为输入，输出为力矩。

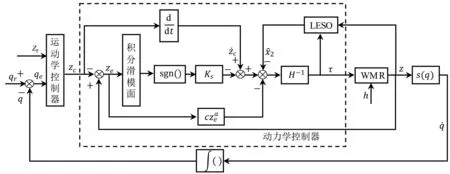
图2 WMR轨迹跟踪控制方案结构框图

2.1 运动学控制器设计

在WMR 轨迹跟踪控制问题中，只需知道位姿向量q中的位置坐标(x,y) 和方向角θ便可知机器人的位置[2,7,12]。因此在运动学控制器设计中，新定义WMR 在全局坐标系下期望位姿状态为qr=[xr,yr,θr]T，WMR 从初始位姿状态q移动到期望位姿qr，位姿误差示意图如图3所示。

图3 WMR位姿误差示意图

由图3 定义位姿跟踪误差为qe=qr-q，其中qe=[ex,ey,eθ]T，WMR位姿误差模型[1]为：

针对WMR 位姿误差模型式(6)，设计如下运动学虚拟速度控制器[3]：

其中，υr和ωr分别为期望线速度和期望角速度；k1和k2均为大于零的常数。

2.2 LESO设计

LESO 将WMR 在运动中受到的扰动扩张成一个新的状态变量x2=h，其中x2=[h1,h2]T，定义状态变量x1=[υ,ω]T，则WMR打滑动力学模型式(5)扩张为：

定义(i=1,2) 为状态变量xi(i=1,2) 的估计值，根据文献[11]对扩张系统式(8)构造LESO为：

2.3 动力学控制器设计

基于实际速度与虚拟控制速度之差设计积分滑模面，将LESO 估计的扰动值前馈，设计于动力学控制器中。定义WMR速度跟踪误差为：

根据滑模控制理论，针对速度跟踪误差（式(10)），带有积分项的滑模面设计为：

其中，c1、c2、a1、a2均为滑模面参数且a1＞0，a2＜1。定义s=[s1,s2]T，c=diag{c1,c2}，a=diag{a1,a2}，则积分滑模面为：

针对WMR 速度跟踪误差式(10)，结合积分滑模面式(12)设计以下动力学控制器：

定理1WMR 在动力学控制器式(13)中参数选择合适情况下，速度跟踪误差式(10)将在有限时间内收敛至零。

由式(5) 和 式(8) 得=Hτ+x2,将其代入式(14)得：

将式(13)代入式(15)可得：

定义ε=x2-为LESO 的扰动估计误差，则式(16)改写为：

根据文献[15]定理2，LESO 的估计误差ε在总扰动h有界情况下是有界的，则存在正数M1，使得‖ε‖≤M1，式(17)由范数的相容性得：

当t＞T时，对式(19)求导可得：

参考文献[17]中定理4.2，求解式(20)可得：

其中，ci∈c，ai∈a，则速度跟踪误差式(10)将在有限时间内收敛至零，由此定理1得证。

3 仿真实验分析

3.1 轨迹跟踪仿真分析

为验证本文基于LESO 观测扰动的优势，给出了其与基于超螺旋干扰观测器(Super-Twisting Disturbance Observer，STDOB)设计的轨迹跟踪控制方案的仿真对比结果。根据文献[18]，基于打滑动力学模型式(5)，超螺旋干扰观测器设计为：

在Matlab/Simulink 仿真中，差速版智能小车（型号L150，轮趣科技（东莞）有限公司）的物理参数见表1。轮式移动机器人的初始参考位姿qr=[0,1,π]T，期望速度υr=1 m/s，ω=1 rad/s，在本次仿真对比实验中选择圆形参考轨迹xr=cost，yr=sint进行仿真实验，仿真时间设定为20 s。仿真中假定的打滑扰动参数见表2。仿真中控制方案参数见表3。

表1 WMR物理参数

表2 打滑扰动参数

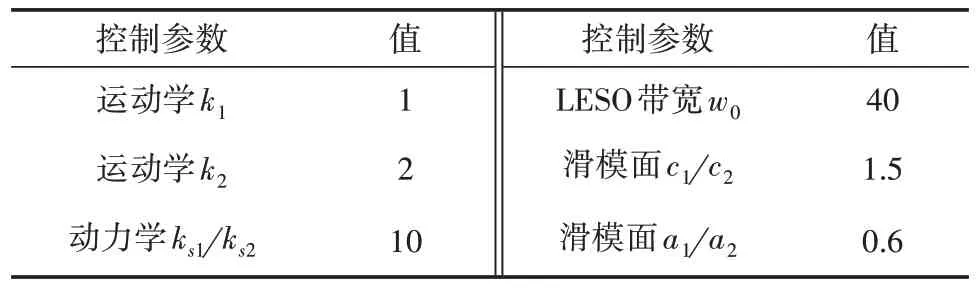
表3 控制方案参数

对LESO 和STDOB 观测下的WMR 圆形参考轨迹跟踪、位置、方向角、线速度和角速度跟踪误差进行仿真对比，对比结果如图4所示。从图4(a)中可以看出，两种观测器下均能跟踪参考轨迹，但LESO 在x轴[-1.0,0.5]及y轴[-1.0,0.5]的14 圆弧段的轨迹跟踪误差比STDOB更小。从图4(b)可以看出两种观测器下的位置跟踪误差均能在一定时间内收敛至零，但在3.0～6.0 s 时STDOB 的位置误差收敛较差，约8.0 s 左右逐渐收敛误差逐渐与LESO 误差一致。从图4(c)可以看出两种观测器下的方向角跟踪误差均能在一定时间内收敛至零，但在约3.5～6.0 s 左右STDOB 方向角误差较LESO 波动更大。从图4(d)可以看出两种观测器下的线速度跟踪误差差别不大。从图4(e)可以看出在1.0～4.0 s 时，STDOB 观测下角速度误差波动更大。

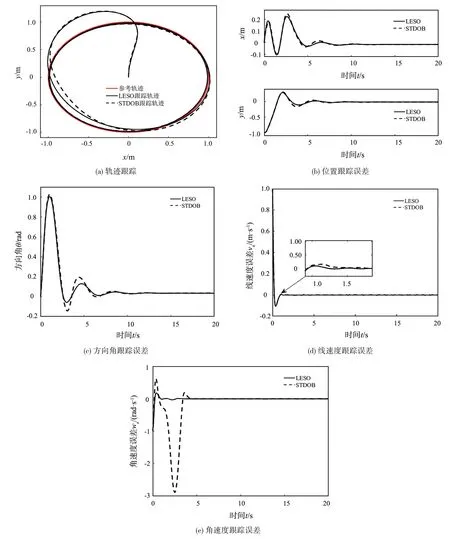
图4 LESO和STDOB下WMR圆形参考轨迹跟踪及其误差仿真对比

3.2 轨迹跟踪仿真收敛性与扰动分析

对LESO和STDOB观测下WMR扰动误差、滑模面和驱动轮力矩进行仿真对比，对比结果如图5 所示。从图5(a)和图5(b)可以看出在LESO观测下扰动误差波动较小，然而在STDOB 观测下扰动误差明显出现锯齿形抖动，这意味着LESO 抗干扰能力强，观测精度较高，收敛误差小。从图5(c)可以看出在LESO 观测下滑模面较快趋于零，且无明显抖动。从图5(d)和图5(e)可以看出在LESO观测下左右驱动轮力矩较STDOB更稳定，无明显抖动。

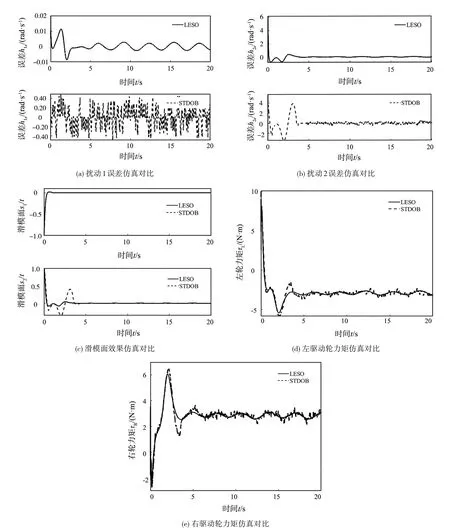
图5 LESO和STDOB下扰动误差、滑模面和驱动轮力矩仿真对比

由图4 和图5 可以看出在LESO 观测下，对扰动误差和滑模面的观测值均能稳定收敛至零，不会发生过多抖动；力矩控制效果也稳定。这可能是因为LESO 对扰动进行估计并对动力学控制器进行补偿时，不依赖于扰动的具体模型，因此本文提出的轮式移动机器人轨迹跟踪控制方案具有良好的抗干扰能力。而STDOB 是通过对系统模型的测量值与其估计值之间的误差进行估计的，在滑模控制设计中边界层切换不光滑而产生抖振现象，使其鲁棒性较差。

本文方法与自抗扰控制不同误差跟踪对比如图6 所示。图6(a)所示为轮式移动机器人在本文方法与文献[12]中自抗扰控制方法下的角速度跟踪误差仿真曲线对比结果，图6(b)所示为两种方法下的X轴跟踪误差仿真曲线对比结果，图6(c)所示为两种方法下的Y轴跟踪误差仿真曲线对比结果。从图6(a)可以看出两种方法下角速度跟踪误差均能够趋近于零，但是自抗扰控制方法要在4.0 s 左右才到达零曲线，而本文方法在2.5 s 左右已达到零曲线，这表明本文方法对角速度的跟踪性能较好。从图6(b)与图6(c)可以看出两种方法下，位置误差均能趋近于零；图6(b)中，X轴跟踪误差在2.0 s 和5.0 s时，本文方法较自抗扰控制方法波动值小；图6(c)中，Y轴跟踪误差在3.5～4.5 s 时，本文方法较自抗扰控制方法曲线波动值小。图6(b)和图6(c)对比结果表明本文方法在4.0 s 左右已经跟踪上圆形轨迹，而自抗扰控制方法需在4.5 s 左右跟踪上圆形轨迹。这可能是因为，本文方法在设计动力学控制器时增加了滑模面控制，而滑模控制响应速度快的优点在轮式移动机器人轨迹跟踪中发挥了作用。

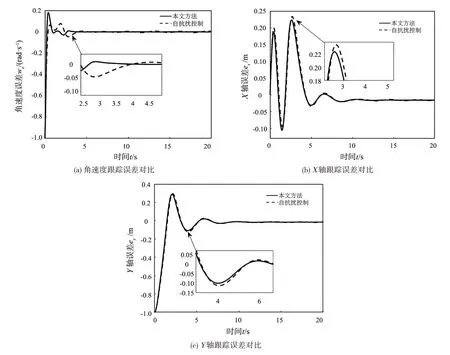
图6 本文方法与自抗扰控制不同跟踪误差对比

4 结束语

为解决车轮发生打滑情况的轮式移动机器人轨迹跟踪问题，提出了一种基于线性扩张状态观测器的滑模控制方案。该方案利用线性扩张状态观测器对系统模型受到的总扰动进行估计，将总扰动的估计值前馈并结合速度跟踪误差的积分滑模面设计了动力学控制器。仿真结果表明该控制方案能够使移动机器人跟踪圆形参考轨迹，位置、方向角、速度跟踪误差能较快收敛至零。与基于超螺旋干扰观测器设计的轨迹跟踪控制方案相比，所提出方案的扰动误差收敛误差小，扰动观测精度更高，滑模面能无抖动收敛至零，左右驱动轮力矩稳定，无锯齿状抖动。