7075铝合金的能量耗散规律及动态损伤本构模型
张艺坤,朱志武
(西南交通大学力学与航空航天学院,成都 611756)
引言
7075 铝合金是一种冷处理锻压合金,具有强度高、抗腐蚀性能强等特点[1],在飞机制造等方面用途广泛。由于机翼蒙皮和梁腹板容易遭受飞鸟或冰雹的冲击,因此研究铝合金材料在高应变率下的力学性能,对于航空航天的发展具有十分重要的工程应用价值和意义。目前国内外对于7075 铝合金的研究主要集中在焊接、材料表面处理和疲劳行为等方面[2],对其在较宽应变率范围内的冲击力学性能、能量损耗规律以及损伤演化理论等方面的研究相对较少。因此,需要结合7075铝合金在冲击载荷下的力学响应以及能量损耗等行为,对该材料在较宽应变率范围内的冲击动态力学性能开展较为系统的研究。
目前,铝合金冲击动态力学性能研究得到了国内外研究者的广泛重视。学者们发现金属材料动态变形最显著的特征即为率敏感性。普遍认为,铝有较低的应变率敏感性。但也有研究表明[3-7],在室温下,当铝及其合金受到103s-1及以上应变率载荷作用时会表现出较强的应变率敏感性。Wang 等[3]开展了2024-T4 和7075-T6 铝合金挤压棒材在不同载荷作用条件下的动态拉伸断裂试验,发现7075-T6合金的初始屈服应力高于2024-T4 铝合金,且2024-T4 和7075-T6 铝合金对应变率的响应不敏感。Lee 等[4]研究了7075 铝合金在冲击载荷作用下应变率和温度对其微观组织演变、断裂机制和剪切局部化发生的影响。Zhang 等[5]利用霍普金森拉杆系统开展了7075-T6铝合金在室温下的动态拉伸试验,发现当进入高应变率区间时,强度增加更为显著,材料的应变率硬化效果明显。Dalai 等[6]使用霍普金森压杆对7075-T651 铝合金进行了1400~5300 s-1之间应变率下的压缩测试,研究了应变率和温度对其力学响应和组织演变的影响,发现材料的流动应力随应变率的增大而增大。Li等[7]对7075和7055 铝合金进行准静态、动态和弹道冲击加载,比较了不同加载条件下的断裂行为,结果表明,7055铝合金的极限抗拉强度、硬度和吸收能力明显高于7075铝合金。
在理论方面,学者们对铝合金材料的动态本构关系也进行了大量研究。其中,Johnson-Cook(J-C)模型[8]应用最为广泛,同时也出现很多就材料特殊性能提出的改进J-C模型。王伏林等[9]对ZL114A铝合金进行了高应变率下的动态力学性能试验,并考虑应变与应变率的耦合作用,提出了一种修正的本构模型——MJC 本构模型,该模型与试验曲线拟合良好。Xiao 等[10]基于J-C 模型,结合广义增量应力状态相关损伤断裂模型,提出了一个新的本构模型。该模型捕获了具有不同应力状态和不同应变率的7003铝合金的延展性和断裂行为,提高了有限元仿真精度。周伦等[11]分析了应变率对6061-T6 铝合金流动应力和应变率敏感性指数的影响,并基于试验结果对J-C 本构模型进行了修正,修正的J-C本构模型可以描述材料的动态塑性流动及断裂失效行为。
近年来,关于描述材料损伤的方法受到了学者们的重视,研究[12-14]发现,可以利用材料损伤前后耗散能量的变化来表征材料所受损伤的程度。目前,对于金属材料在能量耗散原理下的损伤研究较多用于金属复合材料。Quaresimin 等[12]通过研究层合板厚度对吸收能量及接触载荷的影响,提出了一种独立于材料系统的评估复合材料层合板吸能能力的新方法。Farsakh 等[13]根据塑性应变能密度预测纤维复合材料损伤传播,提出了一种评估单向纤维复合层损伤的统一损伤能量模型。卫新亮等[14]研究了复合材料构件在遭受冲击过程中的损伤形态,分析了冲击能量变化对EW200/E51 复合材料层合板的冲击响应及损伤形态的影响规律。
综上所述,虽然国内外对铝合金的动态力学特性进行了许多研究,并初步获得了铝合金在冲击动态下的流动应力变化特征和失效方式,但以往在7075 铝合金的研究中试验应变率相对较低,并且主要集中在研究其抗拉/压强度、微观结构破坏特征等方面,对于材料在更宽应变率范围下的拉伸力学特性、能量演化机制及损伤理论的研究较少,所建立的模型并不能很好地描述7075 铝合金在宽应变率范围内的力学行为。因此,本研究将对7075铝合金进行宽应变率范围内的动态拉伸试验,根据试验结果,分析其能量耗散规律,并基于J-C 本构模型、结合能量损伤理论,获得更符合7075铝合金力学性能的本构模型。
1 7075铝合金拉伸试验
试验采用7075 铝合金原材料作为研究对象,表1列出了该合金的化学元素组成及含量。所有的试样均由同一批次的材料加工而成。

表1 7075铝合金的化学成分 %
1.1 准静态拉伸试验
采用蠕变疲劳试验机对7075铝合金的准静态拉伸性能进行测试,该试验设备主要由主机、温控系统、测变形系统、计算机系统等部分组成,通过引伸计采用应变控制的方式加载。根据GB/T 228.1—2021金属材料拉伸试验第一部分:室温试验方法[15]对试样的要求,此次准静态试验采用哑铃型试样,尺寸如图1所示。
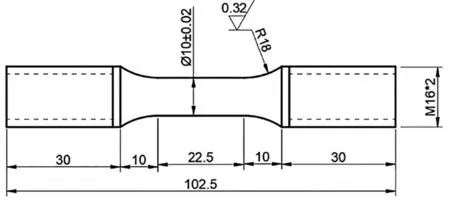
图1 准静态拉伸试样尺寸
本次试验采用的加载应变率分别为0.01、0.001 s-1。得到7075 铝合金在室温下的准静态单轴拉伸应力-应变曲线如图2所示。
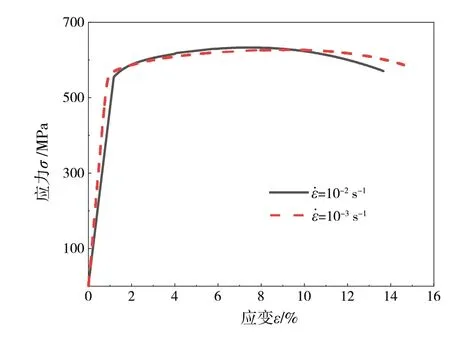
图2 7075铝合金准静态拉伸下的应力-应变曲线
由图2 可见,在弹性阶段,该材料的应力-应变呈线性关系,计算得到材料弹性模量为71 GPa。屈服强度(取塑性变形达到0.2% 时的应力)在600 MPa 左右,并且随着应变率的增加,屈服强度的变化很小,可以忽略不计,因此可认为在准静态拉伸加载下该材料无应变率效应。
1.2 冲击动态拉伸试验
采用分离式霍普金森拉杆系统对7075 铝合金进行室温冲击拉伸试验,该试验系统主要由气室、子弹、入射杆、透射杆和数据采集系统组成。在试验过程中,气室中的高压气体驱动子弹撞击大杆的法兰,产生压缩波,压缩波在法兰的自由端反射,成为拉伸波,并向入射杆的方向传播。当拉伸波到达入射杆的端面时,入射波的一部分被反射回入射杆,另一部分通过试样传输到透射杆[16]。
动态拉伸试验采用的试样为哑铃状,采用螺栓方式与入射杆、透射杆进行连接,具体尺寸如图3所示。

图3 冲击动态拉伸试样尺寸
试验的加载应变率分别为:772、1043、1547、1959 s-1。由于7075铝合金强度较高,拉伸过程中采用波形整形器来保证试样两端的应力平衡。试验得到不同应变率下的波形图,采用下式中的二波法进行数据处理。
得到7075 铝合金在不同加载应变率下的拉伸应力-应变曲线如图4所示。

图4 7075铝合金动态拉伸下的应力-应变曲线
从图4可以看出,在弹性阶段,7075铝合金在不同应变率载荷下的应力-应变曲线基本一致。当应变达到1%左右时,材料到达弹性极限,随后,曲线的斜率也随着应变的增加而发生变化,因为此时的材料进入屈服阶段。在这一阶段比较明显的特征是:流动应力和屈服应力都随着应变率的增加而增加,这表明7075铝合金在高应变率下呈现出显著的应变率效应。当应变达到9%~11%时,应力迅速下降,这是由于材料内部出现了损伤,使材料逐渐失去承载能力,最终发生断裂破坏。
为了进一步研究材料强度与应变率之间的关系,引入动态增长因子(DIF),DIF为试件动态抗拉强度和静态抗拉强度的比值,反映材料在冲击载荷作用下抗拉强度的提高程度[17]。其表达式为:

图5 DIF与应变率关系曲线
由图5 可见,随着应变率的增加,DIF近似呈线性增加,决定系数为0.991,应变率效应明显。产生这种现象的原因主要在于不同应变率下材料的破坏方式以及加载时间长短不同。应变率越高,产生的微裂缝数量越多,会消耗更多能量,然而试件变形的时间越少,材料没有足够的时间用于能量的耗散,因此通过应力增大来消耗能量,从而体现出明显的应变率效应。
分别取出7075 铝合金在4 种应变率下的断裂形态进行观察,可见试件的断口为倾斜型和杯锥型的混合断口,并且颈缩现象明显。由Wang 等[3]的研究可知,材料的断裂方式与起始断裂韧性密切相关,而7075 铝合金的起始断裂韧性较低,因此在冲击拉伸过程中会产生颈缩现象。
2 能量分析
在动荷载作用下,材料拉伸断裂过程涉及到能量的传递和耗散,从能量的角度可以研究材料破坏的本质。为此提出了利用材料断裂前后能量耗散的多少来表征材料所受的损伤程度的观点。在冲击试验中,根据一维应力波理论,子弹被高压气体挤压撞向入射杆,以应力波的形式将子弹的动能传到入射杆称为入射能(记为WI(t)),入射能中的一部分能量转化为透射能(记为WT(t))进入透射杆中,一部分能量转化为反射能(记为WR(t))返回入射杆。应力波所携带的能量统一表示为以下形式[18]:
忽略由于杆件与试样之间的摩擦所消耗的能量,试样在破坏过程中的总耗散能WS(t)为:
由式(5)计算出SHTB 试验中各应力波携带的能量,绘制能量-时程曲线。各应变率下的能量-时程曲线基本一致。7075 铝合金试样的典型能量-时程曲线如图6所示,图中应变率大小为1043 s-1。
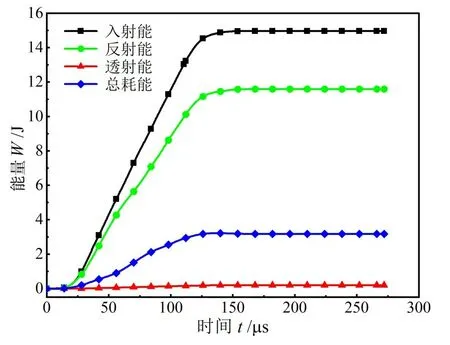
图6 7075铝合金试样在1043 s-1应变率下的能量-时程曲线
从图6可以看出,在0~130 μs内,入射能和反射能随着应力波的传播迅速增加,远大于透射能和总耗散能。这说明入射波在传入到入射杆与试样接触的端面时,大部分能量会反射回入射杆中,少部分能量在应力波穿过试件时被试件吸收,作为耗散能引起试样断裂,其余经过试件后仅剩的少部分能量传递到透射杆中形成透射波。因此,透射能相对于入射能和反射能较小,与前人研究结果[19]一致。入射能、反射能和总耗能在130 μs 左右时达到最大值,分别为:15.0、11.6、3.2 J。最后曲线趋于平稳,表明此时试样已被拉断。
从以上的研究结果来看,7075 铝合金的强度受加载应变率的影响较大,且应力-应变曲线的峰值强度随应变率的增加而增大。为了更加直观地反映试样强度和能量之间的关系,利用耗散能来描述其动态吸能特性。图7 展示了不同应变率下7075铝合金试样的耗散能随时间的变化情况。
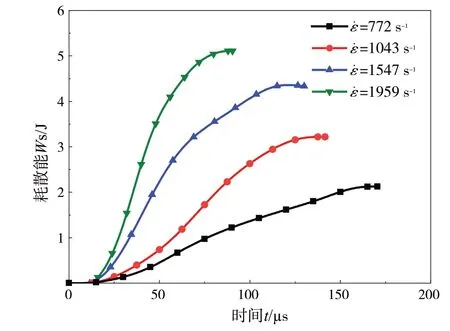
图7 不同应变率下的耗散能曲线
从图7 可见,7075 铝合金的耗散能随着时间的增加呈现出先缓慢增加后快速增加并最终趋于稳定的变化趋势。并且应变率越高,耗散能的增长越迅速。当应变率为772 s-1时,耗散能在167 μs 时平稳,而应变率为1959 s-1时,耗散能在87 μs 时平稳。分析可知,拉伸过程中的初始阶段属于储能阶段,此时还没有裂纹产生。当应变到达屈服强度临界值后,材料进入冲击卸载阶段,此时试样将前期储存的应变能释放,试样完全破坏,随着时间的增长不再耗散能量。应变率越高,材料释放应变能的速度越快,因此耗散能越快趋于平稳。
3 本构模型
在动态本构模型研究中,J-C 模型作为经验型本构模型之一,在铝合金的动态本构模型研究中应用最为广泛。J-C 模型由三部分组成:应变项、温度项以及应变率项。该模型认为,应变、温度和应变率对应力值都是有影响的,但是他们的影响互不干扰,属于完全非耦合模型[20-21],该方程表示为:
式中,σeq为等效流动应力;A为参考温度参考应变率下的屈服应力;B为材料的硬化系数;n为材料的硬化指数;C为与应变率相关的硬化系数;m为与温度相关的软化系数;ε*=/ 为无量纲的应变率,为塑性应变率,为参考应变率;T*=(T-Tr)/(Tm-Tr),为无量纲温度;Tr为参考温度,Tm为熔点温度,T为材料发生变形时的初始温度。
本次试验全部在室温下进行,所以不考虑材料的温度软化效应,式(7)可简化为:
金属材料在加/卸载的过程中材料内部都可能存在不同程度的损伤,从而影响材料的性能。由于能量耗散和冲击速度都与损伤形式密切相关,因此,为了更好地描述材料性质,根据能量耗散理论,定义损伤变量D为[22]:
式中,σc为残余强度;σP为峰值应力;Ud为材料出现破坏时某一时刻所需的耗散能;Ud,max为材料完全断裂状态下所需的耗散能。
由能量守恒定律可知,在动态直接拉伸过程中,外荷载对试样做的功主要转化为试样的弹性应变能及耗散能[23],具体关系式为:
式中,U为外力所做的总功;Ue为材料释放的弹性应变能。Ue表达式如下:
式中,Eu为试样的卸载弹性模量;为试样的卸载泊松比。而单轴拉伸试验中不存在围压,整个加载过程只有轴向应力参与做功,σ1、σ2、σ3为材料的主应力,所以弹性应变能Ue可简化为:
考虑损伤后的动态拉伸本构模型为:
将式(9)中的损伤变量代入式(14)可得:
式(15)为7075 铝合金基于能量耗散理论的动态本构模型。
4 模型参数及验证
根据7075 铝合金准静态拉伸试验和动态拉伸试验所得到的应力-应变曲线,拟合出本构方程中的各项常量参数见表2。
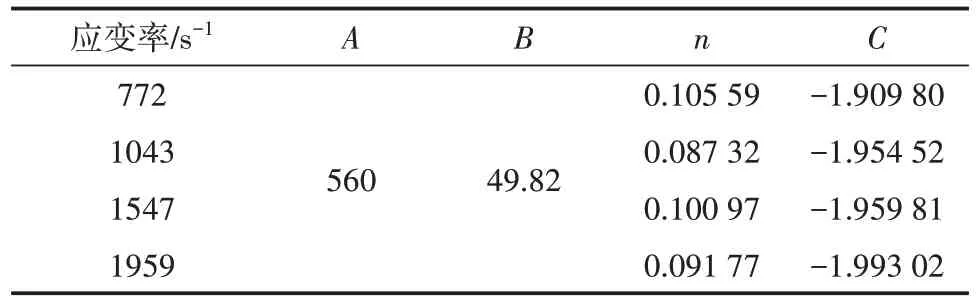
表2 动态本构模型各参数值
根据所求得的模型参数,通过动态拉伸本构模型计算出理论曲线,并与试验曲线进行对比,如图8所示。

图8 冲击载荷下理论曲线与试验曲线对比
对比图8 中7075 铝合金在不同应变率下的应力-应变曲线的理论值和试验值,可以发现理论值与试验值吻合良好。说明本文提出的基于能量耗散理论的动态本构模型可以很好地反映冲击试验中7075铝合金的力学行为,验证了理论的可靠性。
5 结论
本文对7075 铝合金进行了室温下的准静态拉伸试验及冲击动态拉伸试验,得到材料在不同应变率下的应力-应变曲线,讨论了7075 铝合金的拉伸力学性能,分析了其在拉伸过程中的能量耗散规律,得到了7075铝合金的冲击动态本构模型。主要结论如下:
1)7075 铝合金在高应变率作用下具有明显的应变率效应,即随着应变率的增加,材料的屈服应力增高,DIF近似呈线性增加,并且材料断口具有明显的颈缩现象。
2)材料在拉伸断裂过程中,入射能和反射能随着应力波的传播迅速增加。耗散能随着应变率增加显著增高,并且曲线呈现出先缓慢增加后快速增加并最终趋于稳定的变化趋势。
3)采用J-C 本构模型,得到了7075 铝合金在冲击动态载荷作用下的基于能量耗散理论的力学模型。通过理论曲线和试验曲线的对比,验证了模型的合理性。

