深度教学视域下一次课堂案例的实践与思考——关于一道椭圆试题研析拓展的教学实录片段

陈伟流

(惠州市仲恺中学,广东 惠州 516229)

1 研究背景

随着“三新”(新课标、新教材、新高考)背景下教学改革的逐步实施及推广,高考命题的理念已悄然从能力立意转变为素养导向.《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)在命题原则中强调,命题应依据学业质量标准和课程内容,注重对学生数学学科核心素养的考查,处理好数学学科核心素养与知识技能的关系,要充分考虑对教学的积极引导作用;在命题中,应特别关注数学学习过程中思维品质的形成,关注学生会学数学的能力[1].

作为促进学科核心素养在课堂上有效生成落地的基本指导思想之一,深度教学的理念在新时代教育背景下因被广大学者关注、提倡而焕发出别样的生命力.李松林教授曾指出,深度教学是根据学科课堂的3个基点(学科、学生、学习)和大量的实践经验,触及学科本质、抓住学生根本和符合学习本质,最终促进学生学科核心素养发展的教学[2].结合教学实践,笔者认为,深度教学是以学生的学情基础及已有认知经验为出发点,以触及知识背景本源及注重知识整体关联为原则,具备深度体验性及批判性等特征,以培养学生学科核心素养等思维品质为结果目标的教学理念.

以下笔者通过一道椭圆试题的课堂实录案例,将对深度教学理念的理解与思考所得,融入试题研析、背景溯源、技术领路、逆向探索等课堂实践环节,以期与同仁探讨交流.

2 案例呈现

2.1 试题研析,呈现问题

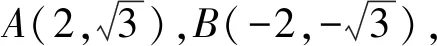
1)求曲线W的方程;

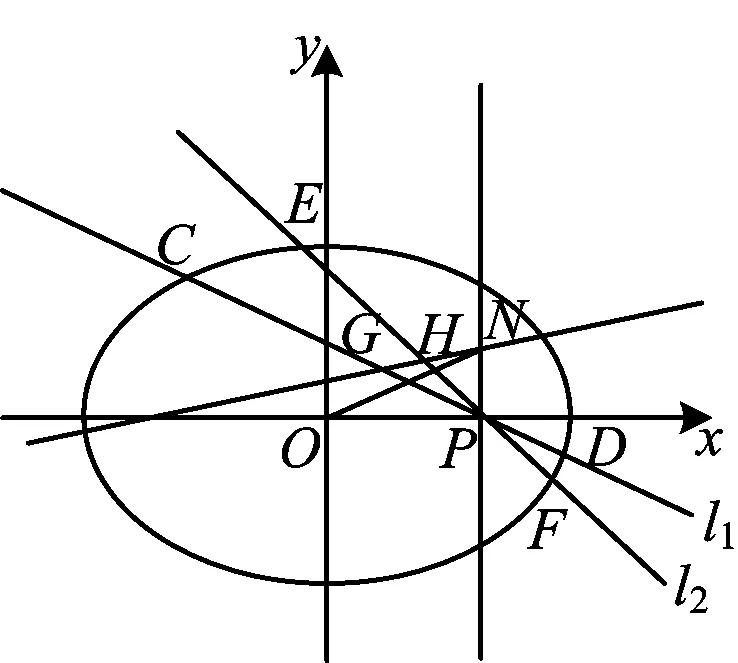
图1

2)如图1,设点P为x轴上除原点O外的一点,过点P作直线l1,l2,l1交曲线W于点C,D,l2交曲线W于点E,F,G,H分别为CD,EF的中点,过点P作x轴的垂线交GH于点N,设CD,EF,ON的斜率分别为k1,k2,k3,求证:k3(k1+k2)为定值．

(2023年广西壮族自治区柳州市统考三模试题第21题)

问题1在设点P坐标为(x0,0)的条件下,如何呈现出点N的坐标以表示k3?

问题2点G既是弦CD的中点,又是直线CD,GH的交点,如何将两种关系与k1进行有效整合?

评注第1)小题以数量积的形式考查轨迹方程,只需设点求解化简即可,属于基础题型;第2)小题以中点弦为切入条件,考查点差法、同构法等解析几何基本思想方法的综合应用,需要教师引导学生理解直线CD,EF在地位上的等价性,并通过线线交点和中点属性得出直线CD,EF斜率的等价表达式,明晰斜率同构思想的来源及作为通性通法在圆锥曲线斜率问题上的普遍适用性.学生通过解题实践,为后续结论的归纳及证明做好铺垫,发展了数学运算、逻辑推理、数学抽象等核心素养.

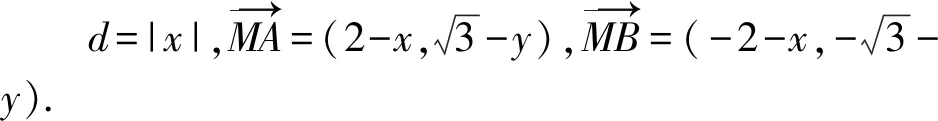
即

得

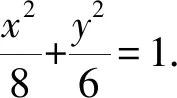
2)证明显然直线GH的斜率存在,设P(x0,0),直线GH的方程为

y=k4x+m,

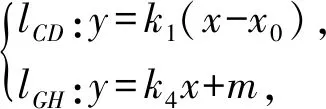
即

设C(xC,yC),D(xD,yD),由点C,D都在椭圆上,得

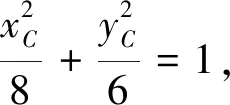
(1)

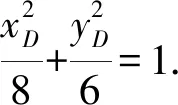
(2)

式(1)-式(2),得

从而

由G为CD的中点,得

化简得

同理可得

故k1,k2为关于k的方程

4(k4x0+m)k2+3x0k+3m=0

的两个实根.由根与系数的关系,得

将x=x0代入直线GH的方程,得

y=k4x0+m,

从而

N(x0,k4x0+m),

即

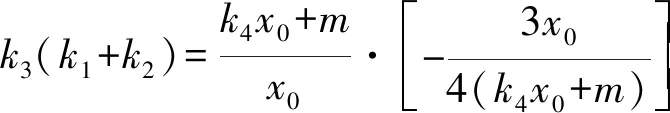
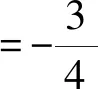
问题3回顾试题解答,3条直线斜率和积的定值结果与点P的坐标无关.若将点O推广为x轴上任一定点(异于点P),其斜率和积是否仍为定值?该如何表示?

评注教师以问题带动学生从解题到研题的过渡性思考,在现代信息技术GeoGebra软件的支持下,以先直观验证定值结果,再抽象总结,归纳证明的学习方式,积累从特殊到一般、从具体到抽象的活动经验,从而把握试题的一般背景.

2.2 背景溯源,揭示本质

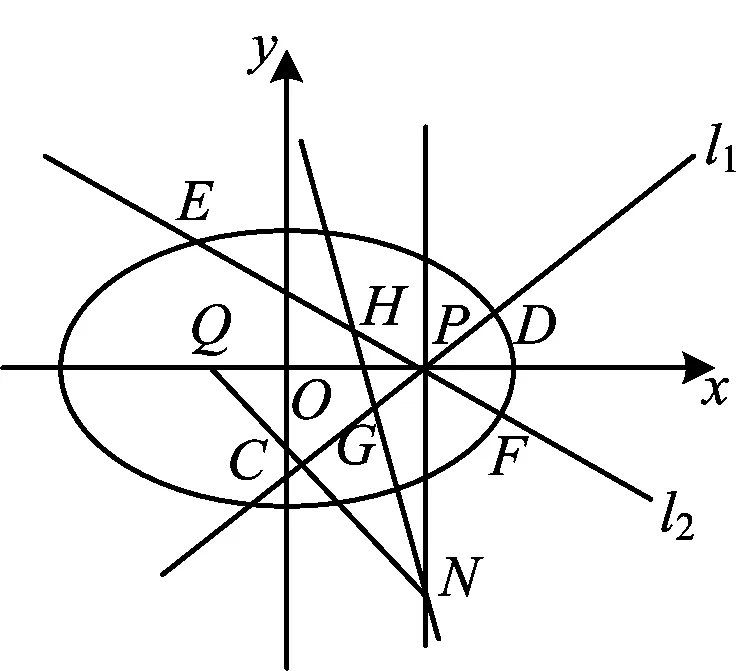
图2

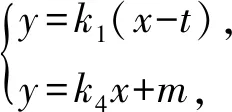
即

因为点C(xC,yC),D(xD,yD)都在椭圆上,所以

即

由G为CD的中点,得

从而

同理可得

可知k1,k2为关于k的方程a2(k4t+m)k2+b2tk+b2m=0的两个实根,得

将x=t代入直线GH的方程,得

N(t,k4t+m),

从而

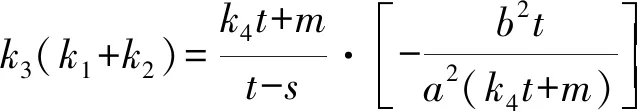
特别地,当Q为原点,即s=0时,有

评注这便是试题的一般命制背景.GeoGebra软件的猜想验证推动了定理1的自然生成.学生在解题中对点差法、同构法形成的认知经验为定理1的推理证明提供了实践可能,使学生在此课堂环节中学有所得、学有所用、学有所悟.

问题4基于椭圆几何图形的对称性,若将点P的位置改在y轴,能否通过类比得到定理1的一个对偶命题.请与同学交流你的成果并在GeoGebra软件上验证命题的正确性.

评注学生在定理1的学习中,通过代数方法得到结论.教师以类比推理的基本思想启发学生探讨定理的多种变化形式,有逻辑地思考、表达并求解问题,丰富了学生内在思维活动和外在学习经验上的层次性,有利于形成重论据、有条理、合逻辑的思维品质和理性精神,从而提升逻辑推理和数学抽象的核心素养.

问题5从定理1、定理2的探索过程知:两弦中点(动点)G,H及坐标轴上的两定点P,Q(O)是决定斜率和积为定值的关键因素,那么这四大要素是否有其内在的必然联系呢?

2.3 技术领路,引申问题

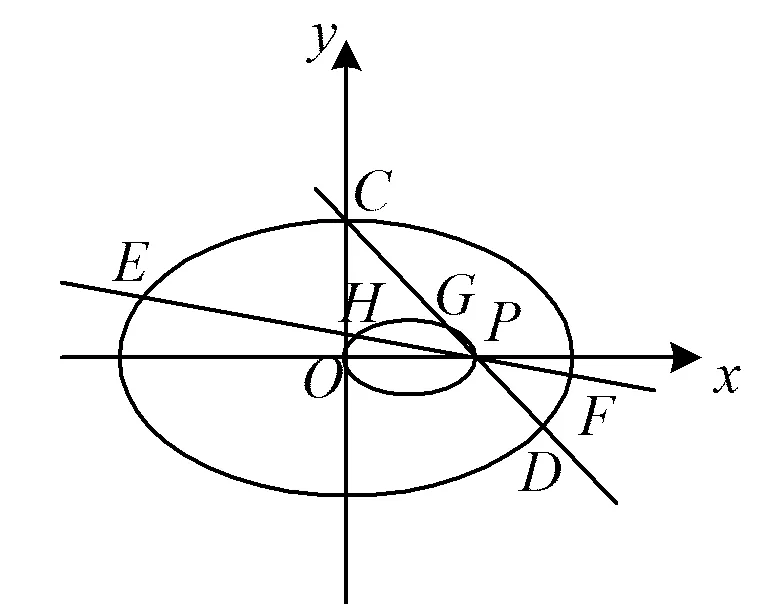
图3

教师在现代信息技术GeoGebra软件中,作出椭圆(如图3)及x轴上的定点P(异于点O),过点P作两相交弦CD,EF,取两弦的中点分别为G,H.学生通过追踪动点G,H并观察G,H的轨迹,归纳总结点G,H,P,O的内在逻辑联系.

问题6立足引理视角,能否对定理1及定理2的内容做出新解读并表达呈现?

评注学生再次通过GeoGebra软件的体验操作,在复杂的情境中把握四大要素的内在关联,为提出椭圆内接顶点三角形的性质构建了过渡性的引理命题,提升了直观想象、数学抽象等核心素养,使知识升华的发生、发展过程循序进阶.

问题7基于椭圆上一定点引出的双直线斜率和积问题,相较于传统直曲联立及斜率同构等解法,齐次式法可以很好地规避方程联立带来的烦琐运算,能否运用此法加以证明?请与同伴们交流该方法的应用心得.

问题8从定理3、定理4的探索知:椭圆的顶点、坐标轴上的定点、过顶点的切线这三大条件是三直线斜率和积为定值的决定因素.若是改变其在条件与结论上的逻辑关系,相应的逆命题是否仍成立?以定理3为例,能否陈述并用齐式法证明相应的逆命题?与同伴交流你的成果并注意数学语言的规范表达.

2.4 逆向探索,完善认知

评注教师通过逆命题的提出,引导学生厘清条件与结论是“知三求一”“等价互逆”“整体封闭”的逻辑关系,以命题的多种变化形式促使学生对定理所蕴含的数学本质及通性规律进行思考、判断、表达、交流,培养数学批判思维,提升数学思维品质.

问题9基于圆锥曲线知识体系的统一性,在圆、双曲线及抛物线中,上述定理是否均成立?是否均有其对应的相关逆命题?如何用数学语言将它们一一呈现?请同学们课后进行类比归纳、梳理总结,并与同伴交流讨论,关注在语言表达上的规范性及定值结果上的准确性.

评注教师通过课后作业的呈现形式,使学生围绕课堂主题,进一步提出命题和模型,并以数学语言加以表征,使得学生习得的知识成高度概括、表达准确、结论一般、有序多级的系统,从而能用更高的观点认识数学结构与知识体系,提升逻辑推理、数学抽象等核心素养.

3 展望思考

3.1 理解“深度教学”,服务“深度备课”

所谓深度教学,并不是教师不顾知识发展、学生学情等实际情况,一味地追求教学内容的深度、难度及广度,而是相对于知识符号的零星识别,相对于解题技能的机械模仿,相对于点到为止的就题论题等浅层教学方式,更多地以知识整体关联为主线,将教学内容循序渐进、螺旋上升、以点带面地展开,使之构成一个可延伸、耐推敲、有活力的有机整体,最终实现教师的深度备课.例如,本案例中,课堂多个环节的实施始终围绕着3条直线的斜率和积定值问题的核心知识点为整体主线统揽全局,并将教学内容的每一步安排都放到课堂活动的大系统中考量,主次分明,目标清晰,结构紧凑,合乎逻辑,而并非片面地突出或强调某一点.

3.2 巧设多维“脚手架”,推进拾级而上

因学生思维视野、知识水平及能力素养方面存在不同程度、不同方面的欠缺,本案例中试题的求解分析及结论的归纳证明等过程必然使部分学生备感吃力而心生畏难情绪.因此,笔者根据知识、学情、技术等客观因素,在深度备课中进行多维预设,围绕内容主线设置符合学生认知规律的启发性问题,不断研究与学习,探索出适合学生知识发展、能力成长的多维脚手架(如图4).通过引入同构法、齐次式法、GeoGebra软件验证、轨迹探路等多个过渡性环节,逐级铺垫,使得定理的归纳、证明、升华、推广等内容得以顺利开展,学生知其然,更知其所以然,如此才能带动学生的思维品质、学习能力不断地拾级而上.

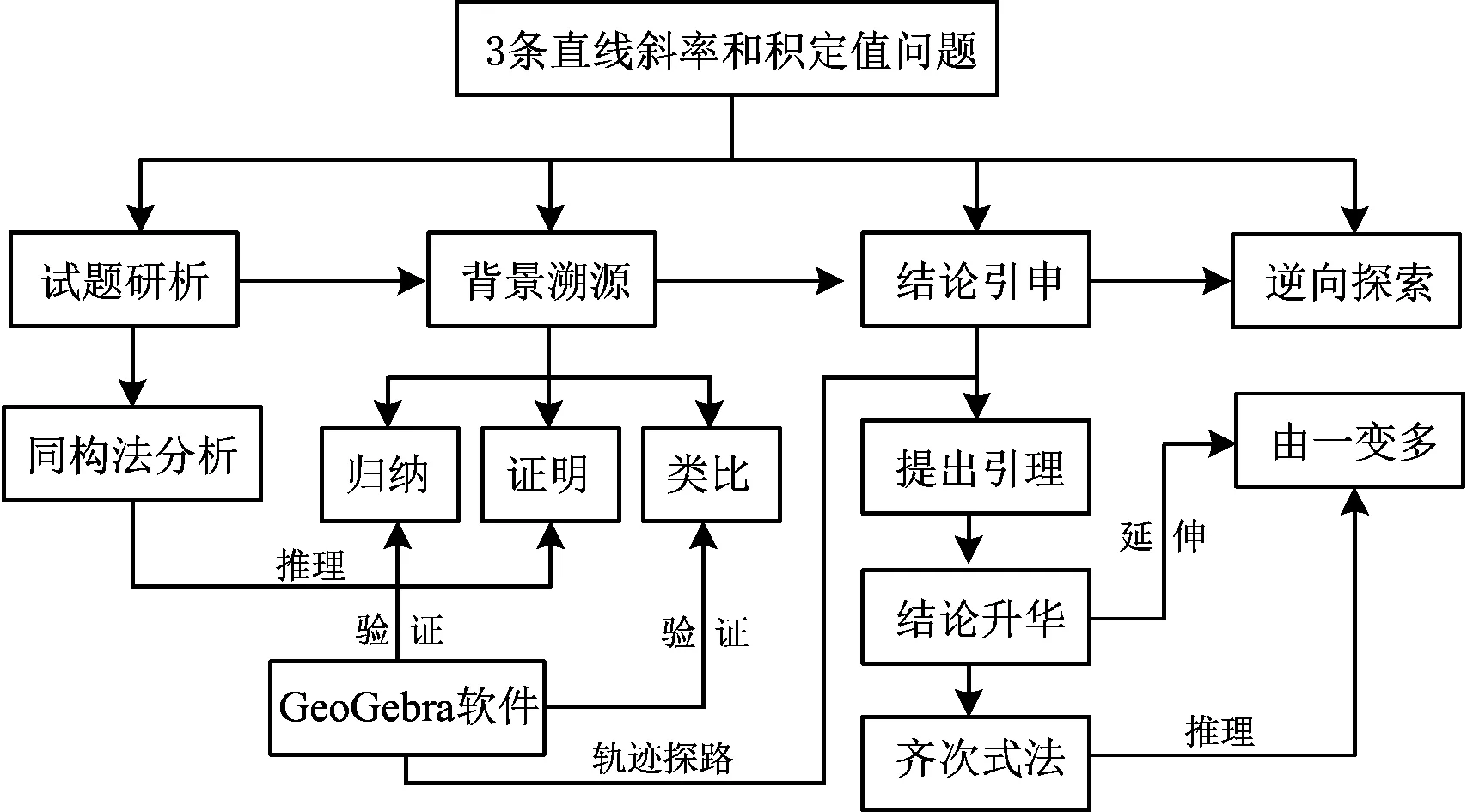
图4

3.3 关注能力成长,提升学习品质

《课标》在实施的教学建议中强调,教师要加强学习方法指导,帮助学生养成良好的数学学习习惯,敢于质疑、善于思考,理解概念、把握本质,数形结合、明晰算理,厘清知识的来龙去脉,建立知识之间的关联.结合深度教学的内涵可知,知识技能、思想方法的习得只是浅层教学中的低阶要求,学生在数学思维、数学语言、实践能力、批判精神、创新能力等学习品质方面的发展和精进,才是深度教学所指向的彼岸远方——深度学习.在本案例中,教师通过问题的精心设计和脚手架的巧妙安排,无不是为了让学生能立足“四基”以发展“四能”,在探寻不变性及规律性的过程中,激发数学学习的兴趣,培养良好的学习习惯,提升数学应用意识、审美价值等理性思维,最终促进学生学会深度学习,引导学生在将来的学习中“会用数学眼光观察现实世界,会用数学思维思考现实世界,会用数学语言表达现实世界”.