先行组织者引领下的小学数学作业设计
王欣

[摘要] 先行组织者是呈现于正式学习材料前的引导性材料,其能够在“已知”与“需知”之间架起“认知桥梁”。在先行组织者引领下,小学数学作业的价值应予重塑,即作为组织者进一步推动学生认知结构的发展。因此,教师在设计作业时要以生为本,不断创新,设置合理的逻辑顺序,促进学生思维向更高阶发展。
[关键词] 先行组织者;小学数学;作业设计
先行组织者,即通过先于任务本身呈现的引导性材料,使用通俗的语言,建立有意义学习的心向,对学生学习数学基本思想、积累数学基本活动经验、发展数学思维、涵育核心素养等,都起到至关重要的作用。基于先行组织者理论,作业设计当以生为本,不断创新,充分发挥其发展认知结构、促进思维进阶的功能。
有意义学习的条件之一是学习材料本身具备逻辑意义,对学习者而言是可接受的,能建立非人为的和实质性的联系。因而,教师需要在充分考虑学情、以生为本的基础上设计作业,还需要注意设置合理的逻辑顺序,促进学生思维的进阶迭代。要发挥作业复习巩固的功能,让作业成为课堂的先行组织者,完善并发展课堂中形成的认知结构,促进高阶思维的产生、发展与进阶。
一、渐进分化:从宏观走向微观
当先行组织者在包容性和抽象概括程度上均高于当前所学内容,即组织者为上位观念时,建议对学习内容的组织采用“渐进分化”策略——先学习抽象性最强的上位知识,再根据学科内容的具体细节逐渐细化,使其包容性和抽象程度递减,越来越具体直观。这一策略多应用于组织教学中,因为人们认识世界大多从一般到具体、从宏观到微观,上位知识的学习大多先于下位知识。而在作业设计中,上位组织者可能是对具体知识点的归纳复习,对学习内容的上位知识的拓展。
例如,我们认识数及其组成用的是十进制计数法,认数是下位知识,进制是上位知识,对低年段学生来说,数是生活中能接触到的,而进制这一知识抽象性过高,苏教版小学数学四年级下册“认识多位数”中“你知道吗”板块有对“二进制”的介绍,结合二年级对算盘的认识,可这样设计作业:
二进制是现代计算机领域中广泛采用的一种计数方法,二进制用“0”和“1”两个数字来计数,进位规则是“满二进一”,我们可以把十进制数转换成二进制数:
十进制数 1 2 3 4 5 6 7 8 ……
二进制数 1 10 11 100 101 110 111 1 000 ……
(1)根据上表填空。
十进制数10=二进制数( )
二进制数10 000=十进制数( )
(2)古时人们常用十六进制计算法,它的进位规则是“满十六进一”。同学们在二年级认识的现代算盘是“五珠算盘”,1个上珠和4个下珠,古时传统算盘则是“七珠算盘”,2个上珠和5个下珠。你能用“进制”的知识解释一下其中的原因吗?
本题通过对“进制”这一上位组织者的介绍学习,让学生了解“二进制”“十六进制”等不同的计数法则和位值原理,通过不同计算法的数字转换和算盘等具体事例,降低“进制”的抽象性与包容性,在细节上彰显上位观念,帮助学生深入了解十进制计算法中数的组成。
二、逐级归纳:从零散走向系统
当先行组织者在包容性和抽象概括程度上均低于当前学习内容,即组织者为下位观念时,建议对学习内容的组织采用“逐级归纳”策略——先学习抽象性最低的下位知识,再根据抽象性递增的顺序进行归纳,逐级归纳策略与渐进分化策略互为逆过程。在作业设计中,当学生对抽象性较高的内容完成存在困难时,可自主举例探究以形成认识,或者先完成给定的抽象性较低的下位知识,在对比发现中总结规律,准确认知数学概念。
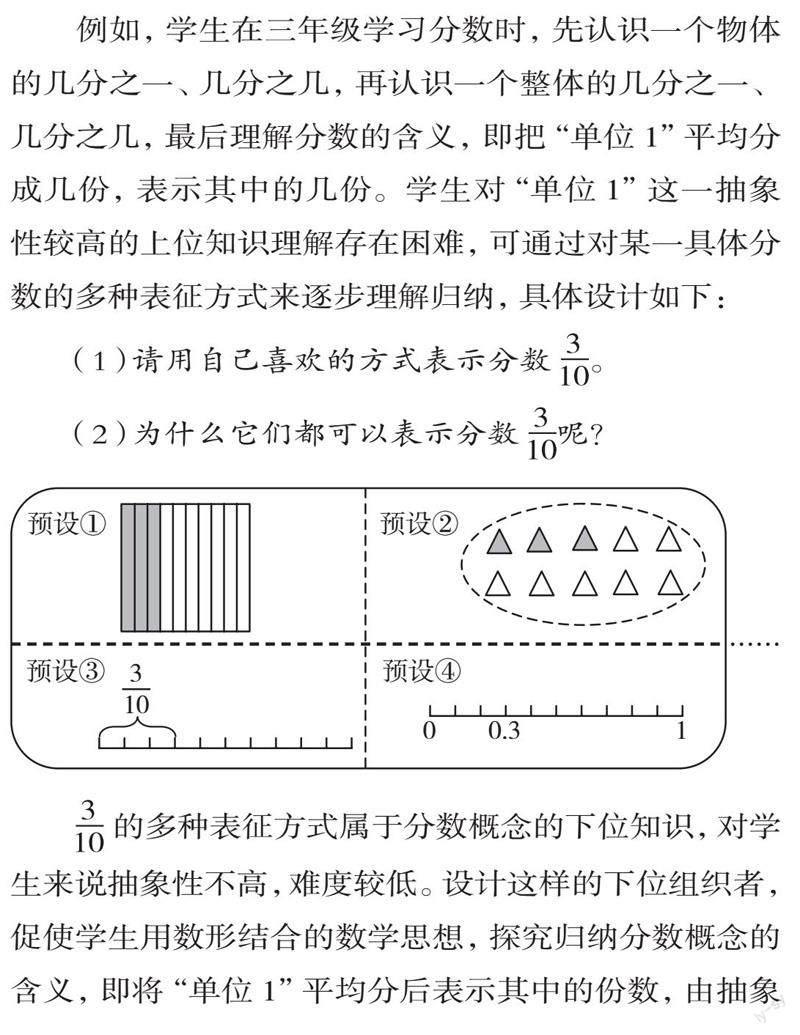
例如,学生在三年级学习分数时,先认识一个物体的几分之一、几分之几,再认识一个整体的几分之一、几分之几,最后理解分数的含义,即把“单位1”平均分成几份,表示其中的几份。学生对“单位1”这一抽象性较高的上位知识理解存在困难,可通过对某一具体分数的多种表征方式来逐步理解归纳,具体设计如下:
(1)请用自己喜欢的方式表示分数 。
(2)为什么它们都可以表示分数 呢?
的多种表征方式属于分数概念的下位知识,对学
生来说抽象性不高,难度较低。设计这样的下位组织者,促使学生用数形结合的数学思想,探究归纳分数概念的含义,即将“单位1”平均分后表示其中的份数,由抽象性较低的下位知识归纳过渡到抽象性较高的上位知识,从零散走向系统,最终使学生建构完善的认知结构,实现思维进阶。
三、整合协调:从模糊走向明朗
当先行组织者在包容性和抽象概括程度上与当前教学内容相差无几时,建议对学习内容的组织采用“整合协调”策略——呈现与学习内容类似的或有共同属性的并列组织者,通过比较明晰概念,帮助学习者对模糊的知识要素进行重组、整合、协调,建立更完备的认知结构。在作业设计中,并列组织者大多用于帮助学生明确易混淆的相似概念或关联知识,这类知识在教学中十分常见。當学生对知识概念的界限不够明晰时,通过相似概念或知识的对比,找到其中的相同与不同,以提升学生的知识迁移与辨析能力,形成对知识网的建构。
例如,四年级初学运算律时,乘法结合律和乘法分配律在应用层面容易混淆,因此在学习乘法分配律时呈现乘法结合律的并列组织者,帮助学生在运算律的对比中找到相同与不同,以理解运算律的概念与法则。
用竖式计算下面两道算式,带※的要验算。
(1)观察上面两道竖式计算过程,选一选,填一填。
①的简便过程可以看作( ),这里运用了( )律;②的计算过程可以看作( ),这里运用了( )律;②的验算过程可以看作( ),这里运用了( )律。
A. 2×909+60×909 B. 99×62×10
C. 62×9+62×900
(2)在□内填入适合的数,使得算式可以使用运算律简便计算。
909×□+990×□ 909×62+990×38+62×□
本题由两道相似的竖式计算作为线索,第一问通过乘法结合律与乘法分配律的对比感受二者的区别,第二问通过运用乘法分配律使算式简便,让学生理解乘法分配律的使用需要以同乘数作为前提。本题借助并列组织者对易混淆的运算律进行整合协调,让认知结构从模糊走向清晰 ,促进学生的思维发展与素养培育。
王 欣 江苏省南京市成贤街小学。

