串联式竖向双锚板抗拔性能数值分析
邹希全,刘 杰,马 越
(湖南工业大学 土木工程学院,湖南 株洲 412007)
1 研究背景
锚定板支挡结构是一种适用于填方的轻型支护结构。它的主要特点有构件断面小、结构质量轻、柔性大、工程量省、圬工数量少、构件可预制,有利于实现机械化施工。同时,锚定板支挡结构很容易与其它挡土结构组合而创新出新的支挡结构形式,而且安装可视、施工质量可控。锚定板种类较多,按照锚定板形状可以分为条形锚定板、圆形锚定板与矩形锚定板。按照埋设深度可以分为浅埋锚定板与深埋锚定板。按照埋置方向可以分为竖向、水平和倾斜锚定板。其中竖向锚定板通过提供水平抗拔力来维持支挡结构的平衡和稳定,其竖向受力特征不具备对称性,常用于填方边坡支挡。
国内外对锚定板锚固系统已有较为系统的研究,主要可分为以下3 类。
1)理论研究。文献[1- 5]针对不同类型锚定板,通过构造锚定板前方土体运动许可速度场,提出了锚定板抗拔承载力极限分析的上限法。文献[6 -7]基于定锚板水平拉拔模型试验和数值模拟试验,研究了拉拔过程中锚定板前方土体的位移变形规律,并在此基础上构建了可考虑埋深等因素变化的竖向锚定板水平拉拔极限承载力学模型,推导出了极限承载力的统一理论解。
2)试验研究。文献[8 -10]通过室内模型试验,获得了锚板周围土体的位移场及剪切应变场,进而研究了土体流动机制及锚板抗拔承载性能。
3)数值分析。文献[11]采用CEL(coupled Eulerian-Lagrangian)法建立数值模型,对锚定板的极限承载力及破坏机制进行了研究。文献[12 -14]基于弹-塑性有限元方法,研究了锚定板前方土体流动机制及抗拔承载力的影响因素;并通过将模型试验和有限单元法相结合,分析了密砂中圆形锚板上拔承载力的尺寸效应。
为了提高锚定板锚固系统的抗拔能力,课题组提出了串联式锚定板锚固系统,此系统是指二块及以上的锚定板由一根拉杆串联而成,锚固系统的抗拔承载力由各锚定板的承载力构成。文献[15]基于室内模型试验,并结合数值模拟,探讨了水平埋设的串联式双锚板间距及埋深对锚定板抗拔承载力及破坏模式的影响。研究结果表明:对于深埋串联式水平埋设的双锚板锚固系统,锚板之间存在一个临界间距,当上下二块锚板间距小于临界间距时,串联式双锚板锚固系统抗拔承载力随上下锚板间距的增大而增大;当上下二块锚板间距大于临界间距时,串联式双锚板锚固系统抗拔承载力几乎不随上下锚板间距的变化而变化;同时,也发现当上下锚板间距从小于临界间距到大于临界间距转变时,串联式水平双锚板周围土体的流动机制则从“土体圆柱形破坏模式”转变为“土体局部独立破坏模式”。
对于串联式竖向埋设的双锚板锚固系统,在水平方向的拉力作用下,前后锚板间距及埋深对抗拔承载力及破坏模式有何影响尚未报导,故本文以粉质黏土中串联式竖向双锚板为研究对象,基于FLAC3D有限差分软件,考虑土体和锚板接触界面摩擦等因素,研究前后锚板间距及埋深等对锚固系统抗拔承载力及其破坏模式的影响。
2 串联式双锚板数值模拟模型
串联式双锚板锚固系统由前后锚板及连接前后锚板的拉杆组成,前后锚板提供锚固系统的抗拔力,拉杆只是一个传力构件(如图1所示)。
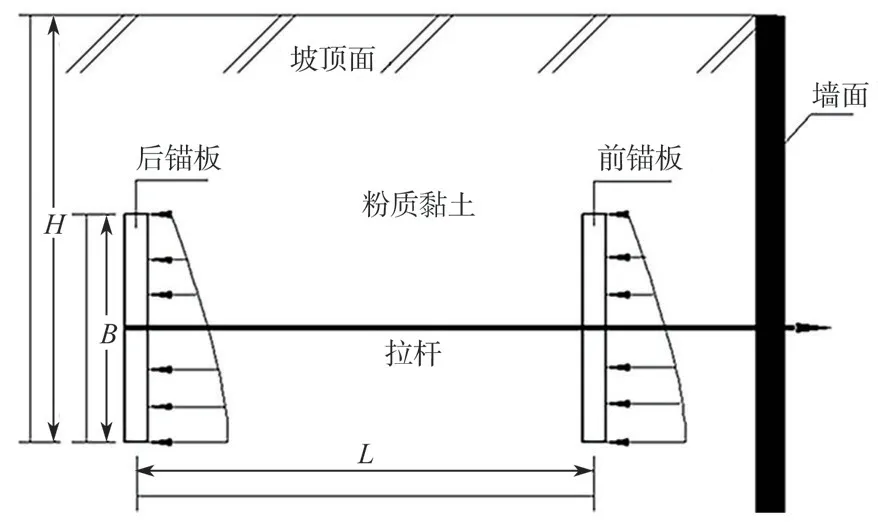
图1 串联式双锚板锚固系统构造示意图Fig.1 Schematic diagram of the construction of the tandem anchor plates anchorage system
为探讨串联式竖向双锚板工作机理及土体流动机制、锚板间距及埋深对串联式双锚板承载性能的影响,采用文献[15]提出的已经通过室内模型试验结果验证了的FLAC3D有限差分模型,探讨串联式竖向双锚板工作性状及影响因素。
在本次数值模拟中,为减小边界效应对数值模拟结果的影响,同时缩短数值模拟时间,首先通过取较大网格尺寸多次试算,合理确定不同锚板埋深、锚板间距等不同条件下的有限差分模型大小。本次数值模拟针对锚板埋深及前后锚板间距对串联式竖向双锚板承载能力影响二种情况,分别采用的最大的数值模拟模型尺寸为9.0 m×3.0 m×6.0 m 和6.0 m×3.0 m×3.0 m。锚板周围土体网格均采用均匀正方形网格。除模型上表面为自由边界外,其余5 个面均为3个方向约束。
FLAC3D拥有多种不同材料和属性参数各异的结构单元,用以模拟真实的结构件,结构单元的建立不仅避免了建立接触面单元的繁琐情况,还能更好地模拟土体与构件相互作用的情况。本次模拟实验中,拉杆使用Cable 结构单元,其计算参数采用了HRB400 的钢筋参数。因为拉杆仅为传力构件,不提供拉杆与土体摩擦,因此,本次模拟实验通过将Cable 结构单元的水泥砂浆锚固体外层相关参数全部置零的方式来实现。
锚板为钢锚板,厚度取50 mm,采用Geogrid 结构单元来模拟,这种单元除提供了Shell 单元的结构性能外,还提供了与土体网格之间交互摩擦的性能。同时,将此结构单元常用的CST 有限单元格式改为抵抗薄膜荷载和抵抗弯曲荷载的DKT CSTH 有限单元格式。为探讨锚板位移与抗拔力之间的关系,监测锚板上节点的位移,与达到平衡后的荷载进行对比,形成位移与抗拔力关系曲线。锚板与土接触面的黏结性能与摩擦性能由FLAC3D提供的弹簧单位面积刚度K、弹簧黏结强度和弹簧摩擦角φ1所决定。其中弹簧黏结强度取锚板周围土体黏聚力的0.6 倍,弹簧单位面积刚度K由FLAC3D中接触面单元所推荐的等效刚度计算式(1)计算:
式中:Kv为锚板体积模量;G为锚板剪切模量;ΔZmin为接触面法向连接区域最小尺寸(网格尺寸)。
弹簧的摩擦角φ1由FLAC3D所提供的估算式(2)确定:
式中φ为锚板周围土的内摩擦角。
本次数值模拟的土体采用摩尔库仑模型,通过在模型中加入土壤重度,并在整个分析过程中保持重力加速度场,直接考察了土壤自重影响的串联式竖向双锚板与土的相互作用机制、前后锚板合理间距及锚板埋深对承载性状的影响,相关数值模拟计算参数取值如表1所示。

表1 数值分析计算参数Table 1 Numerical analysis of calculated parameters
3 数值模拟结果与分析
3.1 前后锚板间距对锚固系统抗拔承载力的影响
本次模拟以串联式方形双锚板为例,方形锚板边长为B=0.5 m。图2 为锚板埋深H=2.5 m、前后锚板间距分别为L=1B、2B、3B、4B、5B条件下,锚板抗拔力与后锚板位移关系对比曲线图。
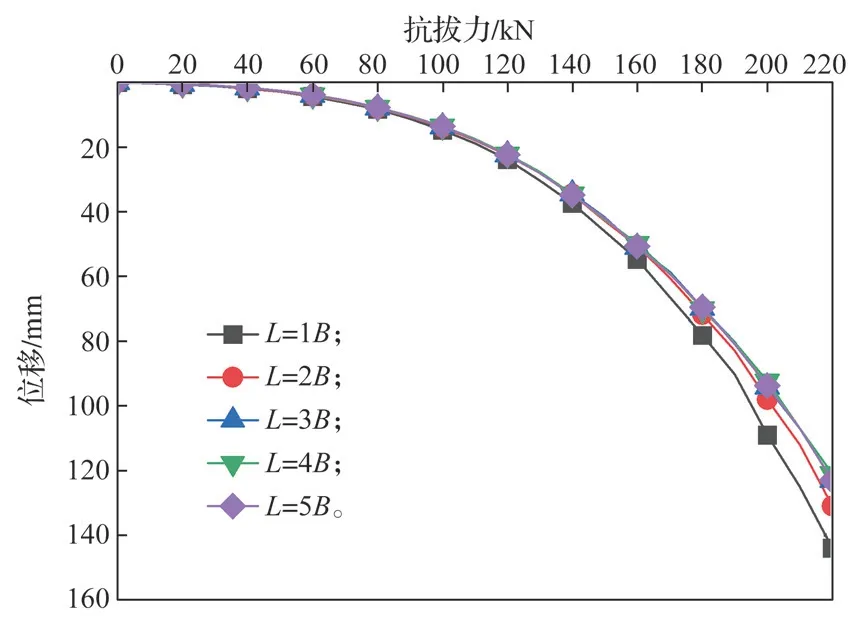
图2 不同锚板间距下抗拔力 -位移关系对比曲线Fig.2 Comparison curves of pullout force displacement relationship under different anchor plate spacing
由图2 可以看出,当锚板间距L≤3B时,锚板抗拔承载力随前后锚板间距的增大而增大;当锚板间距L>3B后,锚板抗拔承载力几乎不随锚板间距的变化而变化。
图3 为锚板埋深H=2.5 m、锚板间距分别为L=2B、3B的条件下,锚板在极限平衡状态时的土体位移矢量图。

图3 不同锚板间距下的土体位移矢量图Fig.3 Soil displacement vector diagram under different anchor plate spacing
由图3 可看出,当锚板间距L=2B时,锚板周围土体位移区域有重叠部分。当锚板间距L=3B,前后锚板位移矢量图不再有重叠区域。综合串联式双锚板抗拔力- 位移关系图以及锚板周围土体位移等直线图,可以获得串联式双锚板前后锚板的合理间距为L=3B,也就是当前后锚板间距L≥3B后,前后锚板能够独立发挥自身的承载能力,而不至于产生相互影响。
3.2 锚板埋设深度对锚固系统抗拔承载力的影响
图4 为锚板边长B=0.5 m、前后锚板的间距为L=4B、锚板埋深分别为H=3B、4B、5B、6B、7B的条件下,锚板抗拔力与后锚板位移的关系对比曲线。由图4 可看出,当锚板埋深H<5B时,锚板抗拔承载力随锚板埋深的增大而增加,且增加的幅度较大。当锚板埋深H>5B后,锚板抗拔承载力随锚板埋深的增大而增加的幅度很小。由此可得竖向串联式锚板临界埋深约为H=5B~6B。此深度与文献[16-17]所获得的深埋与浅埋锚板的分界深度很吻合。
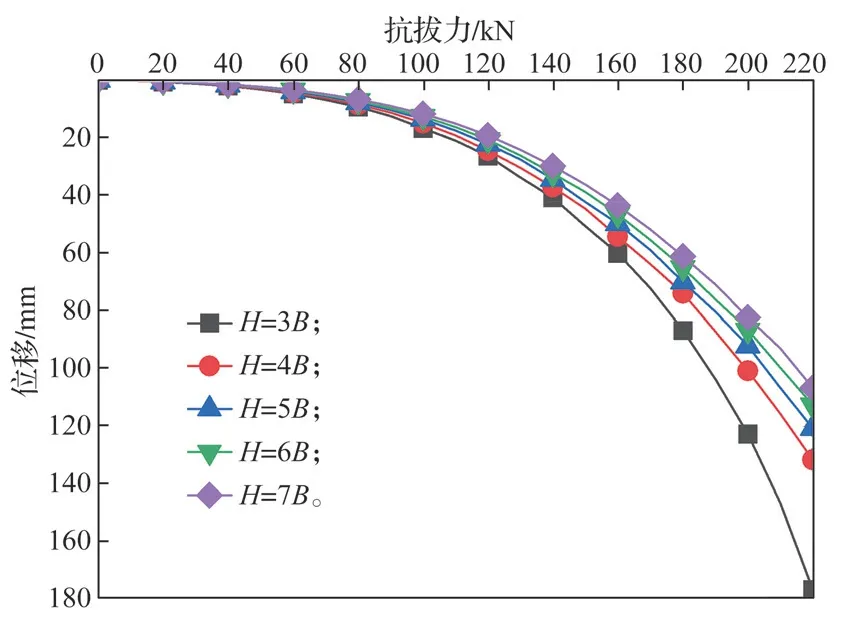
图4 不同锚板埋深时的抗拔力-位移关系对比曲线Fig.4 Comparison curves of pullout force-displacement relationship under different anchor plate burial depths
图5 为锚板边长B=0.5 m、前后锚板的间距为L=4B、锚板埋深分别为H=4B、5B条件下,锚板处于极限平衡状态时的土体位移矢量图。

图5 不同锚板埋深下的土体位移矢量图Fig.5 Soil displacement vector diagram under different burial depths of anchor plates
由图5 可看出,在H=4B与H=5B埋深条件下,无论是前锚板或是后锚板,锚板在拉力作用下向前移动致使锚板周围土体产生位移范围的形状完全不同(如图5 中粗虚线标注的区域)。在H=4B埋深的极限状态下,锚板周围土体流动区域的形状相对锚板中心不对称(如图5 a 粗虚线标注的区域),地表出现向上隆起的位移;在H=5B埋深的极限状态下,锚板周围土体流动区域的形状相对锚板中心几乎对称(如图5 b 粗虚线标注的区域),锚板上方土体位移没有延伸至地表。由此可推定:锚板埋设深度H<5B,锚板周围土体的破坏模式为非对称破坏模式,呈现出浅埋锚板破坏特征;锚板埋设深度H≥5B,锚板周围土体的破坏模式为对称破坏模式,表现为深埋锚板破坏特性。
3.3 土体黏聚力及内摩擦角对锚固系统抗拔承载性能的影响
图6 为锚板边长B=0.5 m、前后锚板间距L=4B、土体黏聚力C为25 MPa、土体内摩擦角φ分别为20°、30°、40°的情况下,串联式锚板周围土体内摩擦角对锚固系统抗拔力-位移关系影响对比曲线。

图6 不同土体摩擦角时的抗拔力 -位移关系对比曲线Fig.6 Comparison curves of pullout force displacement relationship under different internal friction angles of soil
由图6 可看出,锚固系统的抗拔性能随锚板周围土体内摩擦角的增大而增加。
图7 为锚板边长B=0.5 m、前后锚板间距L=4B、土体内摩擦角φ为20°、土体黏聚力C分别为25,35,45 MPa 的条件下,串联式锚板周围土体黏聚力对锚固系统抗拔力-位移关系影响对比曲线。
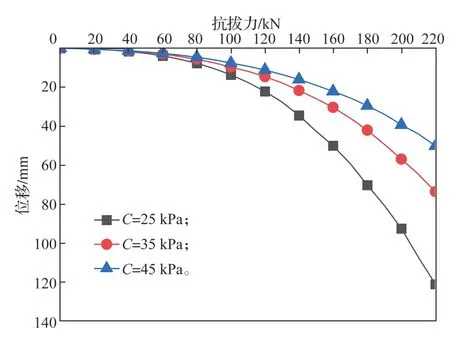
图7 不同土体黏聚力时的抗拔力 -位移关系对比曲线Fig.7 Comparison curves of pullout force displacement relationship under different soil cohesion
由图7 可看出,锚固系统的抗拔性能随锚板周围土体内黏聚力的增大而增加。综合对比图6 和图7,可以看出:提高锚板周围土体内摩擦角比提高土体黏聚力更能有效提高锚固系统的抗拔性能。
4 结论
为提高传统锚定板抗拔承载能力,提出了串联式锚定板锚固系统。基于FLAC3D有限差分软件,建立了串联式双锚板锚固系统与土体相互作用的有限差分模型。探讨了前后锚板间距、锚板埋深、土体黏聚力及内摩擦角对锚固系统抗拔性能的影响,获得如下主要结论:
1)为避免前后锚板的相互影响而降低锚固系统的抗拔承载能力,前后锚板的间距应满足L≥3B。
2)锚板埋设深度H<5B,锚固系统的破坏模式为非对称破坏模式,呈现出浅埋锚板破坏特性;锚板埋设深度H≥5B,锚固系统的破坏模式为对称破坏模式,表现为深埋锚板破坏特性。
3)提高锚板周围土体的黏聚力和内摩擦角均能提高锚固系统的抗拔性能。但提高锚板周围土体的内摩擦角比提高土体的黏聚力更能有效提高锚固系统的抗拔性能。

