一类椭圆型Dirichlet边值问题的高精度Richardson外推法
李曹杰,张海湘,杨雪花
(湖南工业大学 理学院,湖南 株洲 412007)
1 研究背景
椭圆型方程在流体力学、弹性力学、电磁学、几何学和变分法中都得到了广泛应用。随着椭圆型方程应用的不断深入,对其数值解的精度要求越来越高。对这类方程,常见的处理方式是,首先对区间进行网格剖分,然后对方程离散、建立差分格式,再解线性方程组[1]。五点差分格式是最传统的差分格式,但它的精度只有二阶,难以得到高精度的解,不再满足目前的方程应用需要。Richardson 外推法是一种通过线性组合缩小误差的方法,因此,为了寻求高精度的解,采用外推法获取方程的高阶格式是一个不错的选择。在文献[1-2]中,作者基于五点差分格式外推,得到了椭圆型方程的四阶精度格式。文献[1,3-4]发展了四阶紧致差分格式,可以直接求出椭圆型方程四阶精度的数值解。文献[5]提出了多项复合型黏弹性波问题的离散奇异卷积方法。文献[6-8]分别在不同条件下给出了椭圆型方程六阶精度的解,文献[9]通过引入新的变量来构建方程的紧致格式,文献[10]利用Hopf-Cole 变换,将非线性方程变成线性方程。如此可以借助紧算子构建高阶差分格式。文献[11]提出了新的时空平衡的Sinc 配点方法,求解四阶带奇异的积分微分方程。文献[12]提出了ADI 配点方法求解二阶带奇异的积分微分方程。文献[13]提出了计算高维带弱奇异核发展型方程的交替方向隐式欧拉方法。文献[14]构造了二维带弱奇异核抛物型积分微分方程的交替方向隐式有限差分格式。
本文拟基于文献[1]中的四阶紧致差分格式和文献[7]中的六阶紧致差分格式,首先,给出相关引理,搭建四阶差分格式和极值原理,并证明差分格式的收敛阶,在此基础上建立四阶紧致差分格式;然后,用Richardson 外推法,建立椭圆型方程的外推格式,分别得到其六阶与八阶的高阶精度格式;最后,以两个算例来验证高阶格式的有效性。
现讨论如下一类椭圆型Dirichlet 边值问题:
其边界条件为
式(1)(2)中:Ω为矩形区域[0,L1]×[0,L2]内部;Γ为边界。
将区间[0,L1]作m等分,记h1=L1/m;将区间[0,L2]作n等分,记h2=L2/n,则矩形区域被剖分成m×n个矩形小块。
为表示方便,本文引入如下记号:
对结点表示如下:
在结点处考虑方程(1),有
为了引入紧致差分法,定义如下x和y方向紧算子:
2 理论基础
引理1如果函数g(x)在区间[c-h,c+h]有八阶连续偏导,则
证明由带微分余项的Taylor 公式,有
将式(7)和(8)相加,整理后有
对g的二阶导数应用Taylor 公式求解,可得
由式(10)(11)可得:
将式(12)减去式(9),并应用积分中值定理及介值定理,可得
引理1 证毕。
引理2设
为Ω上的网格函数,记
当步长h1、h2满足
则有
证明采用反证法,若
记
则一定存在内部结点(i0,j0)使得vi0,j0=M,且其周围结点至少有一个的值严格小于M,因此当步长满足上述关系时,有
这与题设矛盾,故假设不成立。引理2 证毕。
引理3紧算子A、B定义如式(4)(5)所示,有如下差分格式
这里g(xi,yj)≤0,若步长满足如下关系:
记
为上述差分格式(21)的解,则有
证明由g(xi,yj)≤0,有
简记g(xi,yj)为gi,j,再记
定义网格函数
则有
因此有
由引理2,有
于是
引理3 证毕。
3 数值离散格式
3.1 紧致差分格式
现设u(x,y)有八阶连续偏导,在式(3)两端同时作用紧算子AB,因为AB=BA,可得
由引理1,记Ui,j=u(xi,yj),整理得:
为使算式简洁,记误差项
将式(35)(36)代入方程(34),整理得到
省去误差项,用数值解ui,j代替真解Ui,j,得到如下紧致差分格式:
3.2 高阶Richardson 外推差分格式
若p(h)可近似表示为
用h/2 代替h,得
结合式(39)(40),有
定理1设定解问题
存在光滑解,则有
证明记
差分格式(38)的误差方程组为
将式(42)(43)离散后有
记
记
由引理3,且φ=0,有
用(h1/2,h2/2)代替(h1,h2),得到
结合式(53)与(54),再根据式(41),可得
定理1 证毕。
利用文献[7],可得一个具有六阶截断误差的差分格式:
通过定理1 类似证明,容易得到如下八阶外推格式:
同样,通过外推原理,可以对四阶格式(38)进行两次外推,得到如下两次外推八阶格式:
4 数值算例
本节将给出数值算例,以验证本研究所建立方法的有效性,以及在数值求解椭圆型Dirichlet 边值问题时的高效性。表1 和表2 中列出了算例1 与算例2 在四阶格式(38)、六阶格式(55)(56)、八阶格式(57)(58)下的数值结果。其中,E(h1,h2)表示在步长h1、h2下网格结点的最大误差,且Rate=log2(E(2h1,2h2)/E(h1,h2)),CPU time(s)是差分格式算该步长数值解的时间,总CPU 是程序连续运行完各步长结果的总时间。
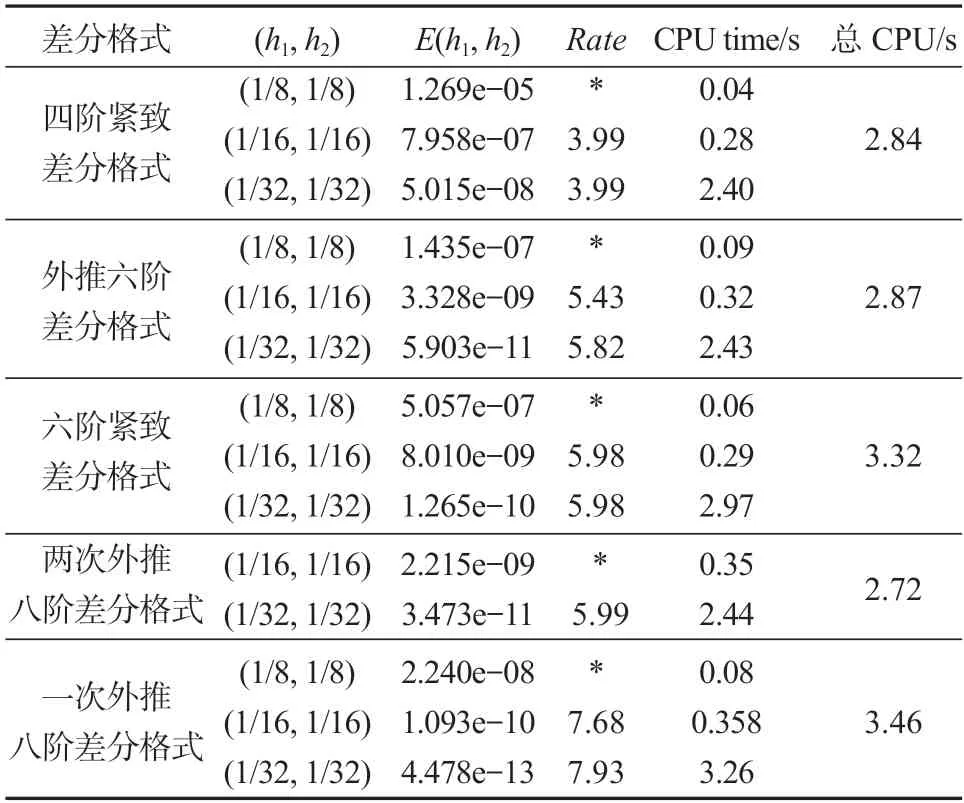
表1 算例1 数值结果Table 1 Numerical results of example 1
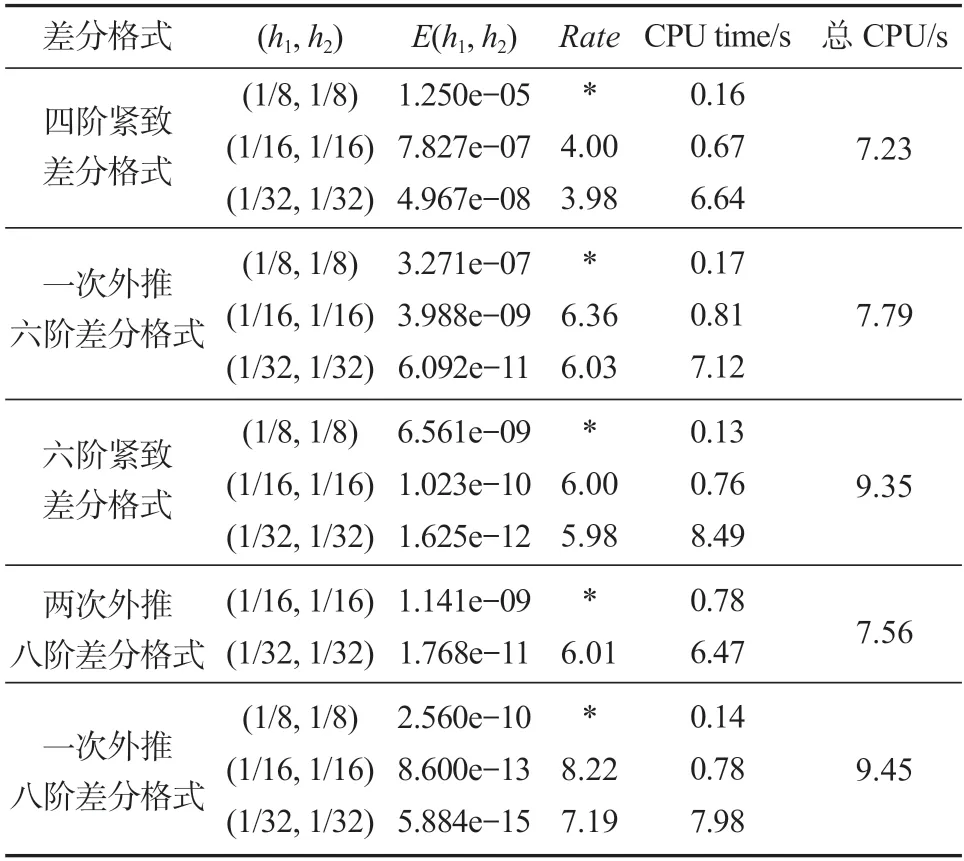
表2 算例2 的数值结果Table 2 Numerical results of examples 2
算例1
算例2
两个算例中,一次外推六阶差分格式与一次外推八阶差分格式分别建立在四阶、六阶紧致差分格式上。从表1 和表2 中,可以看到一次外推能将收敛率提高两阶。在相同步长下这能得到更高精度的数值解,且解的收敛速度更快。两次外推八阶差分格式建立在四阶紧致格式上,其L∞误差值均低于理论预期值,因此,绘出其误差曲面并求出部分结点值,以进一步探究其原因。算例1 在步长为1/32 和1/64 时的误差曲面如图1所示,其不同结点处的误差值与最大误差值具体见表3。
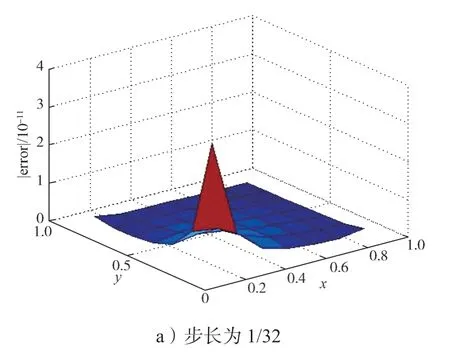
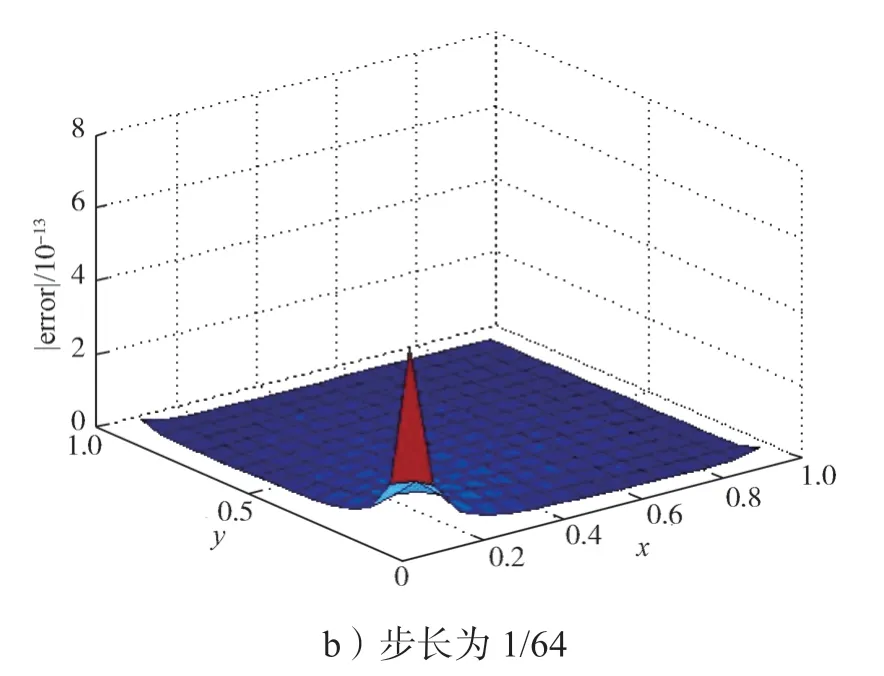
图1 算例1 在不同步长下的误差曲面Fig.1 Error surface of example 1 with different step lengths

表3 算例1 不同结点处的误差值与最大误差Table 3 Error values and maximum errors of example 1 at different nodes
算例2 在步长为1/32 和1/64 时的误差曲面如图2所示,其不同结点处的误差值与最大误差值见表4。
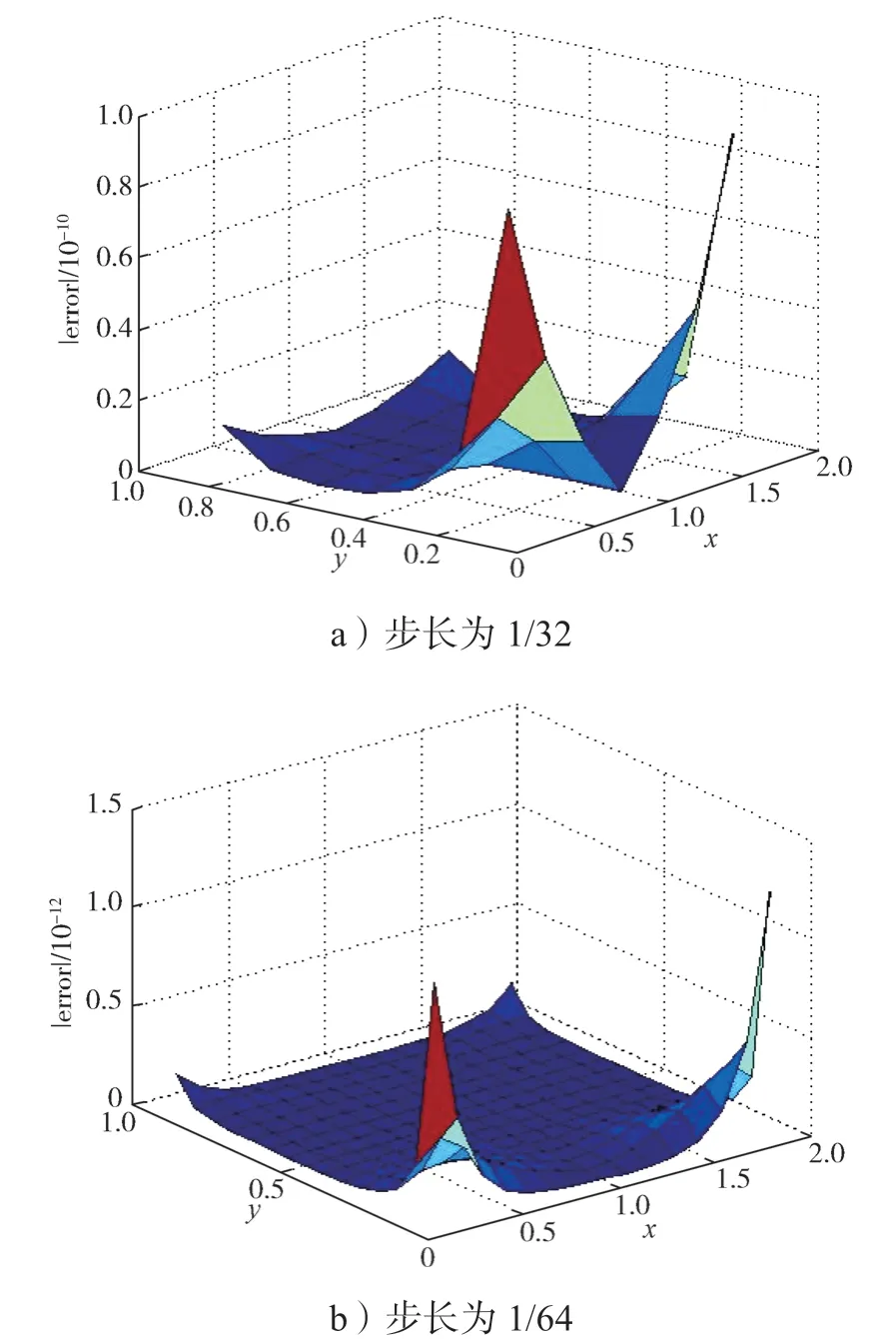
图2 算例2 在不同步长下的误差曲面Fig.2 Error surface of example 2 with different step lengths

表4 算例2 不同结点处的误差值与最大误差Table 4 Error values and maximum errors of example 2 at different nodes
从图1 和图2、表3 和表4 中的数据可以看出,对比某一固定结点时,例如表4,在结点(1/2,1/4)处,其收敛率分别约为8 和9,由此可见算例收敛率符合理论预期。从图1 和图2 中可以看到,同一步长下,有些结点的误差值相对较大,并且可以发现当步长不同时,其误差最大值在不同结点处取得,Rate=log2(E(2h1,2h2)/E(h1,h2))约为6,因此在前文的表1 与表2 中,二次外推格式的整体收敛率只达到了6 阶。接下来计算二次外推格式的L2误差收敛阶,两个算例的L2误差及收敛率结果如表5所示,表中的Rate=log2(L2(2h1,2h2)/L2(h1,h2))。
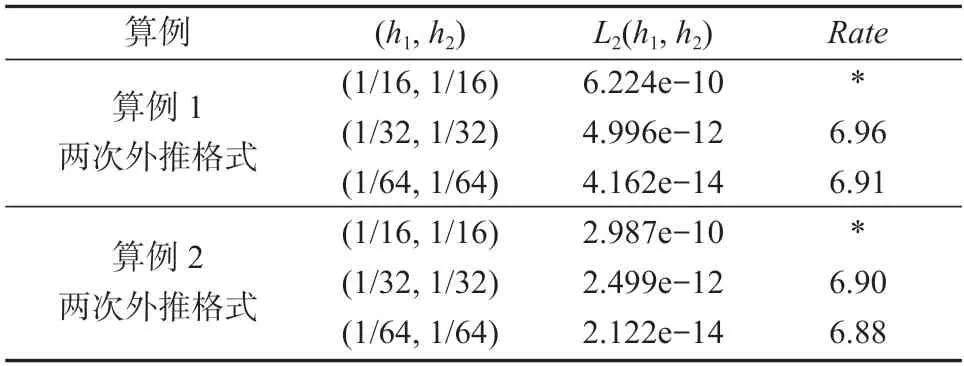
表5 两个算例的L2 误差及收敛率Table 5 L2 error and convergence rate of two examples
表5 显示,两个算例在不同步长下的L2收敛率都约为7 阶收敛,即数值方法得到的收敛率略小于理论的8 阶收敛。可能的原因是:每一次步长的计算结果需要由3 种不同步长的数值解通过线性关系得出。而3 种不同步长的数值解本身就会产生舍入误差,在高精度下三者叠加会影响到截断误差的收敛率。由此多次外推法有一定的局限性。
5 结语
本文研究了以基于紧致差分格式的高精度Richardson 外推格式来求椭圆型偏微分方程的数值解,理论显示一次外推能将精度提升两阶。算例对比了原紧致差分格式、外推高阶差分分格式和同阶紧致差分格式的数值结果。结果表明,外推高阶差分格式虽然比原格式要花费更长的时间进行运算,但同步长下得到解的精度大大提升。且外推差分格式运算时间不一定比同阶紧致差分格式更长,总CPU 时间甚至可能会更短,外推格式时间主要取决于原格式程序的运算简易程度。两次外推八阶差分格式理论上能达到八阶,但由于结果会受到多次舍入误差的影响,使得计算结果受到影响。L∞误差只达到了六阶收敛;L2误差收敛率在七阶左右。两个算例的结果均显示,外推八阶格式精度符合理论预期。总的来说,Richardson 外推法对于提高差分格式的精度有显著作用,且易于理解与使用,便于在差分格式中广泛利用。

