临坡条形锚板抗拔承载力试验及理论分析

李青，艾志诚

(1.中国核电工程有限公司郑州分公司，河南 郑州450052；2.湖南大学 土木工程学院，湖南 长沙410082)

锚板基础因具有施工方便、经济等优点而广泛运用于信号塔、海洋工程、边坡支挡等岩土工程领域。在近几十年中，大量国内外学者采用模型试验[1-6]、有限元数值分析[7-8]、极限平衡分析[9-12]和上下限定理[13-14]等方法对埋置在平地的锚板抗拔承载力开展了研究。锚板也常用作于临近边坡构筑物的抗拔基础，如山区信号塔，海洋钻井平台等，因此对临近边坡锚板抗拔承载力进行研究具有重要的工程意义。近年来，Bhattacharya 等[7,13,15-17]对临近边坡锚板的抗拔承载力开展了研究，Bildik等[15]采用PLAXIS 有限元软件分析了临近砂土边坡锚板的抗拔承载力，研究了锚板的埋置比λ(锚板埋置深度H/锚板宽度B，下同)、边坡角度α(下同)、临坡比ε(锚板边缘到坡角的水平距离d/锚板宽度B，下同)和不同砂土密实度(下同)对于锚板抗拔承载力的影响；Ganesh 等[13]采用上限法得到临近砂土边坡条形锚板在地震力作用下抗拔承载力的理论计算公式，根据该公式可知，抗拔承载力随着锚板的埋置比、临坡比和砂土内摩擦角φ(下同)的增大而增大，随着边坡角度的增大而减小；Bhattacharya[7]和Khuntial 等[16]运用有限元分析方法，分析了临近黏性土边坡锚板的抗拔承载力。以上关于临坡锚板抗拔承载力的研究大多基于理论分析，而锚板极限抗拔承载力的确定，与其破坏面形态紧密相关。为此，很多学者基于不同的假定，提出不同破坏面形式，其大致可分为直线型[3,4,10,18-20]破坏面和曲线 型[1-2,5,21-22]破坏面。Mors[20]首次提出了倒楔形破坏面,假定破坏面与竖直方的夹角等于砂土内摩擦角φ，Bobbitt 等[18]则认为该夹角为φ/2；Ilamparuth 等[3]通过室内模型试验研究了浅埋和深埋圆形锚板分别埋置于松砂、中密砂、密砂地基中的承载能力。结果表明：对于浅埋锚板，破坏面与竖直方向的夹角为φ/2，而深埋锚板只在锚板周边形成气球状的局部剪切破坏带，因此提出了锚板在松砂、中密砂、密砂中的临界埋置比分别4.8，5.9 和6.8；LIU 等[4]开展了砂土中圆形锚板的室内模型试验，在试验中借助DIC 图像关联技术得到了锚板上拔时土体的破坏面为一倾斜的直线，破坏面与竖直方向的夹角的大小随锚板的埋置比、砂土的密实度有关；Deshmukh 等[10]假定破坏面为直线，且与竖直方向的夹角为φ/2，借助Kötter 方程计算了锚板的抗拔承载力，并与前人的试验和理论结果进行了对比。如上所述，大量学者对于埋置于平地的锚板的破坏面开展试验或理论研究，并提出了不同形式的破坏面，只有Ganesh 等[13]采用上限法理论推导了砂土中临坡条形锚板承载力，采用的破坏面为锚板两侧对称的直线型破坏面，破坏面与竖直方向的夹角为φ。但该方法的破坏面为作者的假定，缺乏相关的验证依据。由以上研究可知，临坡锚板破坏面的文献极为少见，而相关的破坏面假定却缺乏试验的依据，可见，对临坡锚板开展试验研究以探求其破坏面形态，并由此确定出临坡段条形锚板的极限承载力尤为必要。鉴于此，本文首先通过借助DIC 图像关联技术开展不同边坡角度(α=0°，15°，30°和45°)和不同的临坡比(ε=0，1，2，3 和4)的一系列室内模型试验，重点讨论不同边坡的角度和临坡比对于锚板抗拔承载力的影响。然后根据DIC 得到的砂土位移及锚板上拔前后砂土的变形特点，得到临坡条形锚板的破坏面基本规律，并基于极限平衡方法推导计算临近砂土边坡条形锚板抗拔承载力的理论公式，以便工程应用。

1 临坡锚板抗拔模型试验

1.1 试验设备

临坡条形锚板抗拔承载力模型试验设备主要由试验模型箱、锚板、加载反力架、整合位移与力传感器的伺服液压动作器、液压加载控制系统及DIC 设备组成，如图1所示。模型箱由3 面钢板与2 面透明钢化玻璃通过螺栓固定而成(DIC 高清相机通过透明玻璃可观测到土体变形)，模型箱的内部尺寸为2 100 mm×800 mm×500 mm；锚板则由厚度为10 mm 的钢板制成，尺寸为498 mm×100 mm，其长宽比L/B为4.98，可看作为条形锚板[23]；锚板通过圆环与伺服动作器上的圆弧型挂钩连接，以给锚板施加竖直向上的上拔力荷载，通过电脑操作的液压加载控制系统进行加载，力与位移的数据能实时保存至电脑中。DIC 设备包括高清相机、图像处理程序及泛光灯，高清相机对锚板及周边的砂土进行拍摄，其拍摄的图像经过图像处理程序后处理可以得到锚板及周边砂土位移，模型箱上方的泛光灯给相机提供了良好的照明环境。

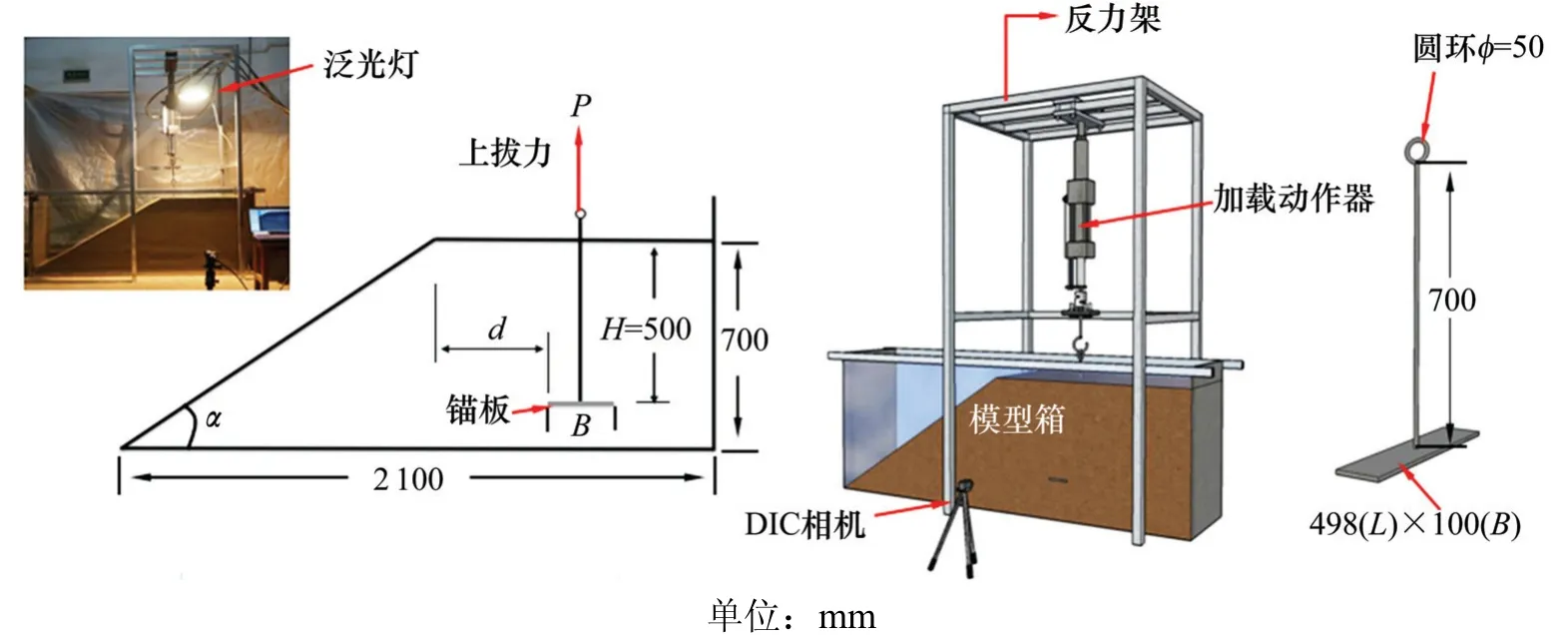
图1 试验设备Fig.1 Test equipment

1.2 试样制备与加载

试验中采用的砂土为室内风干河砂，其物理性质指标如表1所示。在每组试验中砂土的密实度(γ=16.6 kN/m3)保持一致，试验过程中采用分层压实法构筑试验边坡，每层填筑的砂土厚度为70 mm，其用量根据边坡角度的不同进行计算得到，当砂土堆填到200 mm 高度时，将锚板放置在预先标定位置，然后继续采用相同的方法将砂土堆填至700 mm高，每一组试验锚板的埋置比λ=5。

表1 土的物理性质指标Table 1 Property of sand in test

本试验共开展了12 组不同边坡角度和临坡比的锚板抗拔测试，其具体试验布置如表2所示。通过电脑控制锚板的上拔速度为2.4 mm/min，为保证锚板已充分上拔，当锚板上拔位移达到60 mm 时停止试验。在锚板上拔过程中，DIC 相机每隔2.5 s拍摄一张图像，直至锚板上拔完成后停止拍摄，其拍摄的图像保存至电脑中。

表2 试验安排表Table 2 Arrangement of model tests

2 试验结果与分析

2.1 锚板的抗拔承载力

试验过程中首先进行一组埋置于平地(α=0°)的锚板的抗拔试验，而后进行不同边坡角度(α=45°，30°和15°)临坡锚板的抗拔对比试验，图2～5 分别为不同边坡角度临坡锚板上拔过程中的荷载位移曲线图。从图2～5 可知，所有的荷载位移曲线均表现出相同特征：随着锚板开始上拔，荷载急剧增加达到荷载的峰值点；达到峰值点后锚板位移继续增加，荷载随后开始缓慢下降趋于一稳定值；当荷载曲线达到峰值点后趋于水平时开始出现波动。为便于研究条形锚杆的极限承载力，将抗拔承载力根据式(1)转化为抗拔承载力系数Nγ，如图2～5 所示，取每组荷载位移曲线中荷载的峰值点为锚板的极限抗拔承载力Pu，根据公式(1)可以得到各组试验的抗拔承载力系数，列于表3所示。

式中：γ为土体的重度；A为锚板的面积；H为锚板的埋置深度。

图2 埋置于平地时锚板的荷载位移曲线图Fig.2 Load displacement curves when anchor is buried in horizontal ground

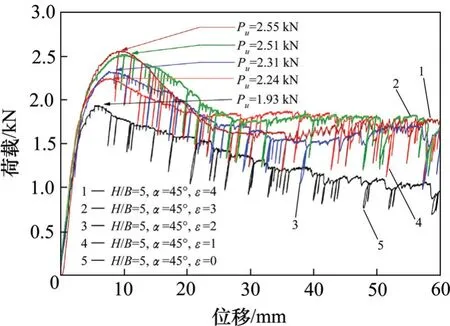
图3 当α=45°，不同ε时锚板的荷载位移曲线图Fig.3 Load displacement curves with different εwhen α=45°

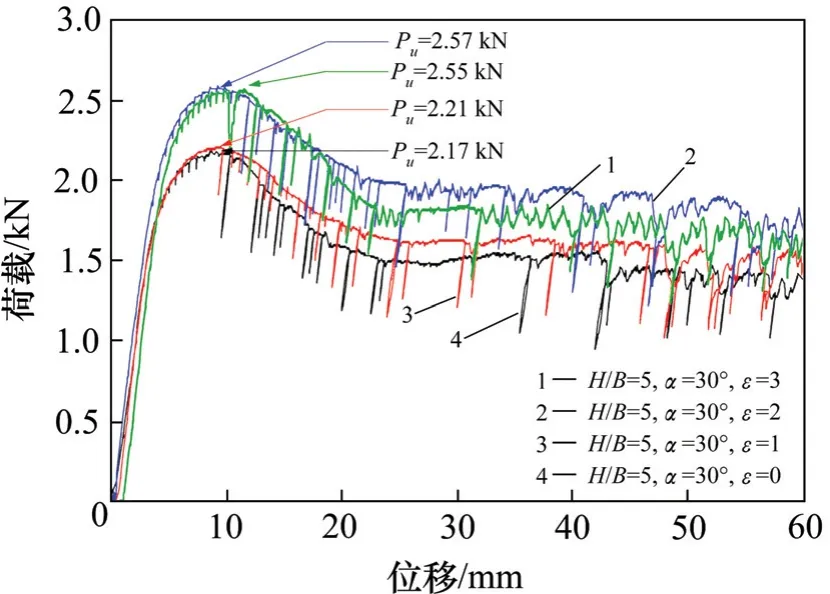
图4 当α=30°，不同ε时锚板的荷载位移曲线图Fig.4 Load displacement curves with different εwhen α=30°

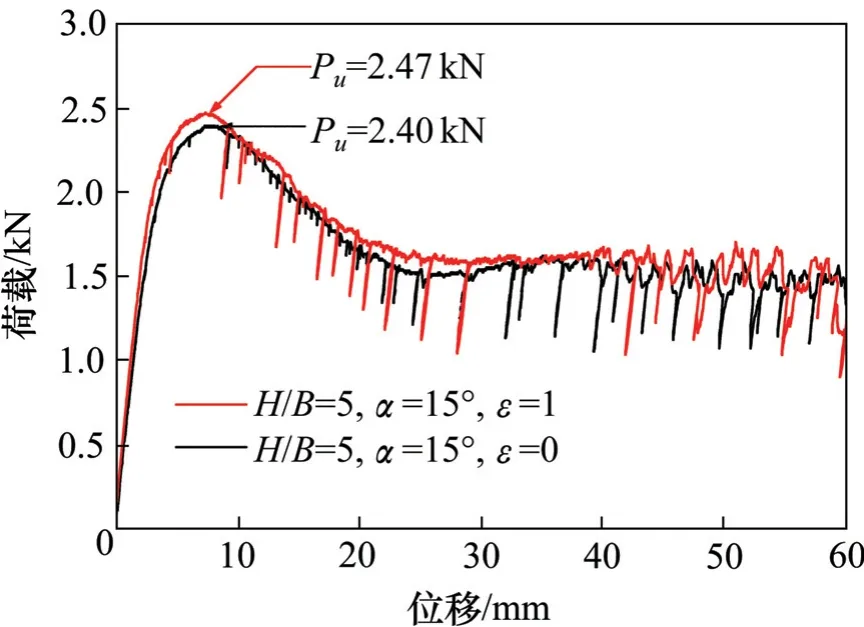
图5 当α=15°，不同ε时锚板的荷载位移曲线图Fig.5 Load displacement curves with different εwhen α=15°

从表3可知，当锚板临近边坡时，锚板抗拔承载力系数随着临坡比的增大而增大，但当临坡比增大到一临界值时，锚板的抗拔承载力系数不再增大且趋向于平地锚板的抗拔承载力系数，即存在临界值，设该临界值为临界临坡比εr，显然，对于不同边坡角度，εr的值也不相同，如从试验中得到的荷载位移曲线可知，当α=15°时，εr介于0～1 之间，当α=30°时εr介于1～2 之间，当α=45°时，εr介于3～4之间，边坡的角度越大，相应的临界临坡比也越大。同时，边坡的角度也对锚板的抗拔承载力有很大的影响，当ε=0，α=0°的锚板抗拔承载力系数比α=45°的大45%，当ε=1 时，α=15°的锚板抗拔承载力系数比α=45°的大10%。

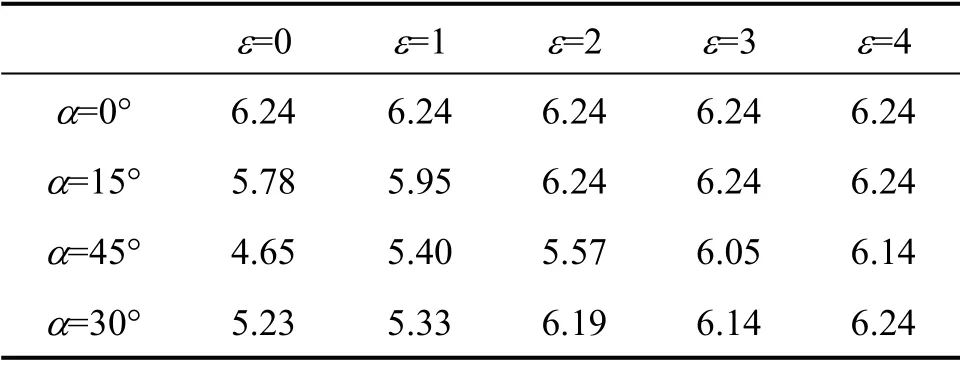
表3 试验抗拔承载力系数NγTable 3 Uplift factor Nγof model tests

2.2 土体破坏面分析

DIC 图像关联技术可以得到每组试验中砂土的位移路径，同时通过对比锚板上拔前后土体表面的变形，可以得到砂土的变形分界点，如图6所示，为研究方便，本文根据DIC 得到的砂土位移和土体表面的变形分界点将土体的破坏简化为直线型破坏面[3,10,19]，连接锚板边缘与临界变形点的直线SL和SR即为锚板两侧土体的破坏面，破坏面SL和SR与竖直方向的夹角分别为θL和θR。采用相同的方法可分别得到埋置于平地和临近边坡锚板的破坏面，如图7～8 所示。其结果如表4中所示，对比表4中各组数据可知，当临坡锚板ε＜εr，锚板左右两边的破坏面呈非对称布置；边坡角度越大，θL越大，θR越小；而在同一角度边坡，ε越小，θL越大，θR越小；当ε≥εr，此时临坡锚板的破坏面与平地的相同。

由上述分析可知，在θL和θR确定后，破坏面也随之确定。为此，根据表4中的各组试验的θL和θR，对锚板两侧的破坏面SL和SR分别用直线FL和FR对破坏面SL和SR进行了拟合，其拟合结果如图7～8和表4中所示，拟合直线FL和FR与竖直方向的夹角为βL和βR。βL和βR的取值为2 种情况：当ε＜εr时，βL和βR的表达式分别如式(2)和式(3)所示；当ε≥εr时，βL和βR取值为φ/2(与平地情况破坏角相等)。根据式(2)得到εr的表达式如式(4)所示。

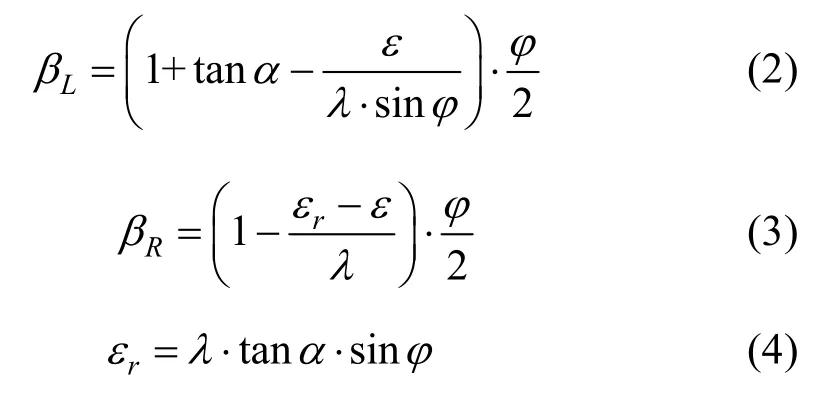
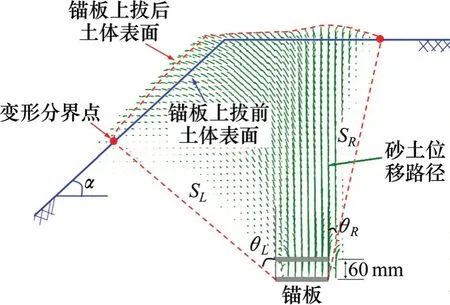
图6 土体破坏面确定示意图Fig.6 Schematic diagram of soil failure surfaces

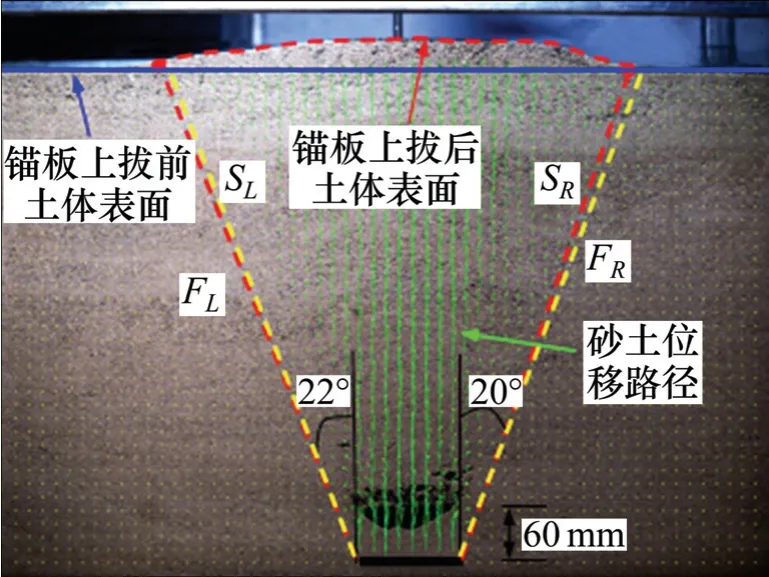
图7 埋置于平地锚板的土体破坏面Fig.7 Failure surfaces of soil when anchor is buried in horizontal ground

图8 临近45°边坡锚板的土体破坏面Fig.8 Failure surfaces of soil when anchor is adjacent to a slope with 45°

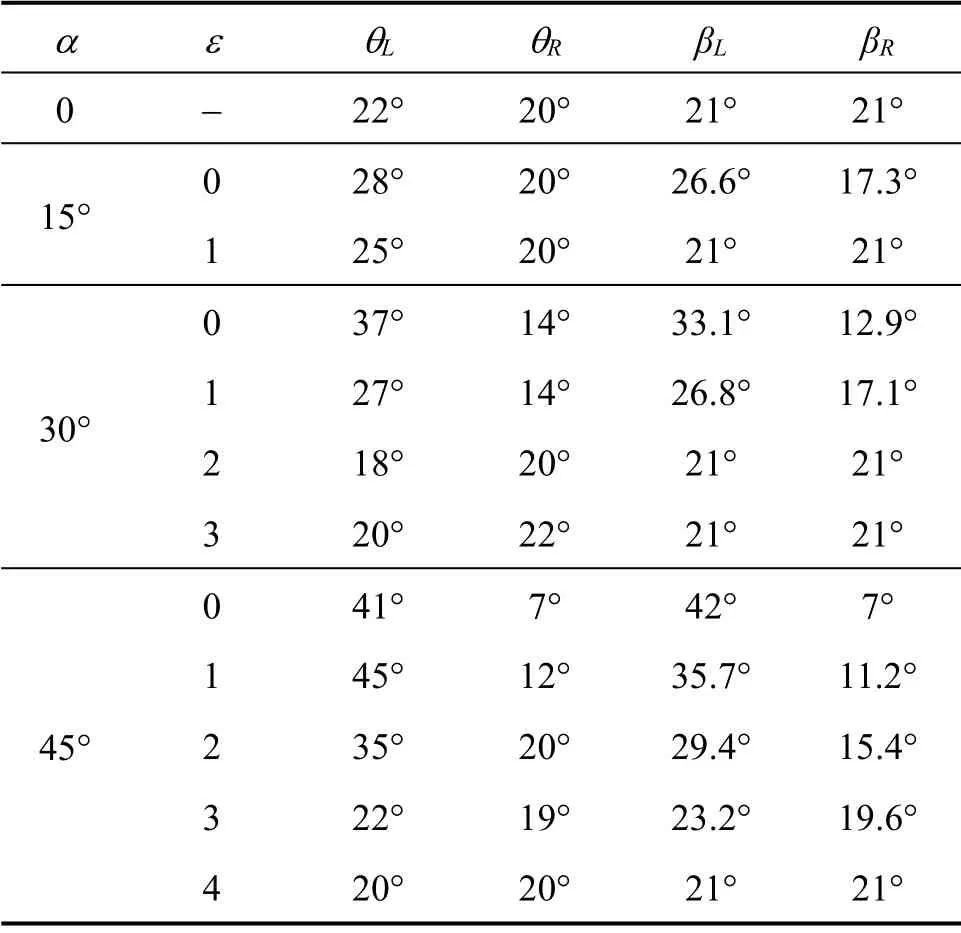
表4 试验破坏面和拟合破坏面与竖直方向的夹角Table 4 Angle between the experimental and fitting failure surfaces with the vertical direction

根据式(2)和式(3)计算得到的βL、βR值列于表4中，可知，拟合直线FL和FR可以较好的对破坏面进行拟合。

3 抗拔承载力理论计算公式

得到条形锚板的破坏面形态后即可得到其承载力表达式，为了简化抗拔承载力的计算过程，本文假定砂土服从Mohr-Coulomb 破坏准则。

综上所述，完善工程量清算工作，对于进行电力工程造价控制而言非常重要。电力工程是一个长期复杂的工程，并不是一朝一夕就能够成的事。在这个过程中要意识到进行工程量清单计价工作的重要性，根据国家相关法律法规的指导意见，改变传统的造价控制工作模式，不断的进行探索、改善，以寻求更加全面的工程量计算工作体系，进而提升电力工程的综合能力。

锚板的极限抗拔承载力Pu的计算示意图如图9所示，显然其大小等于破坏面上土压力竖向分量Rv和破坏面内土体的自重W之和，其中图9(a)为当ε＜εr时的示意图，图9(b)为当ε≥εr时的示意图。Pu的计算公式如式(5)所示，

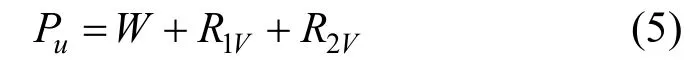
式中：R1V和R2V分别为锚板两侧破坏面上土压力的竖向分量。

对于破坏面内土体的重量W的计算分为2 种情况：当ε＜εr时，

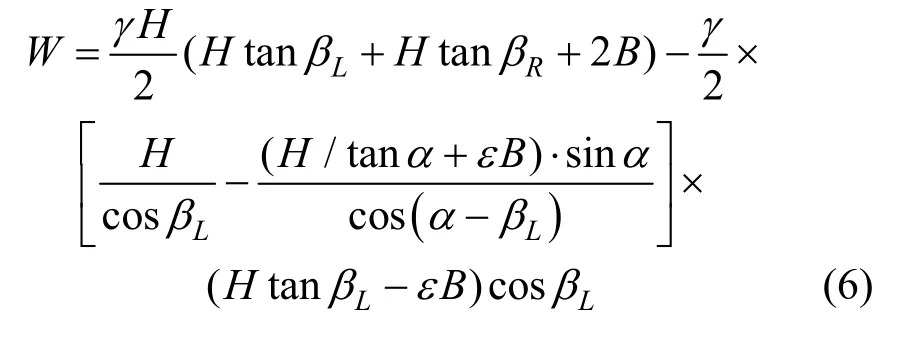
当ε≥εr时，

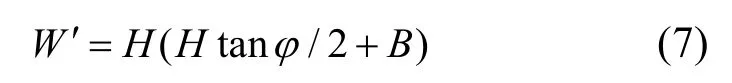
对于计算土压力竖向分量Rv选取破坏面上任一长度为s的微元进行受力分析，如图9(c)所示。根据Kötter 方程可得：

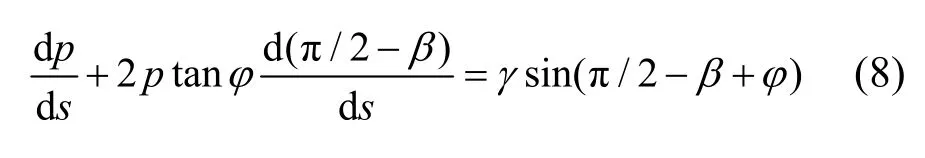
对于破坏面为直线时，

结合式(8)和式(9)可得：

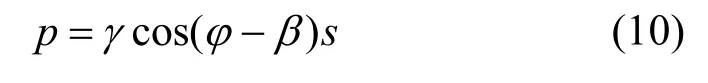
因此对破坏面上的被动土压力进行积分即可得到破坏面上的土压力R及其竖向分量RV。对于RV的计算同样分2 种情况：

当ε＜εr时，

当ε≥εr时，

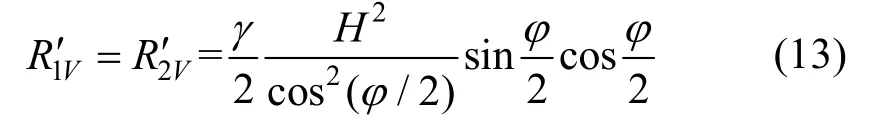
综合上述公式可得临坡条形锚板的抗拔承载力系数表达式：

当ε＜εr时，

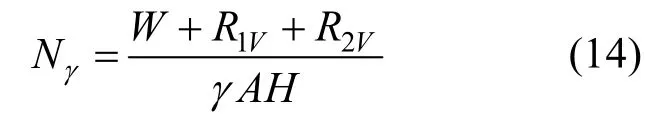
当ε≥εr时，

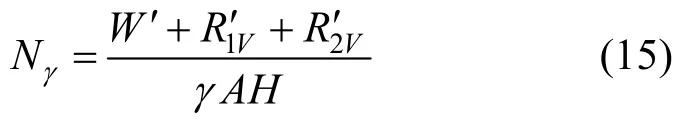
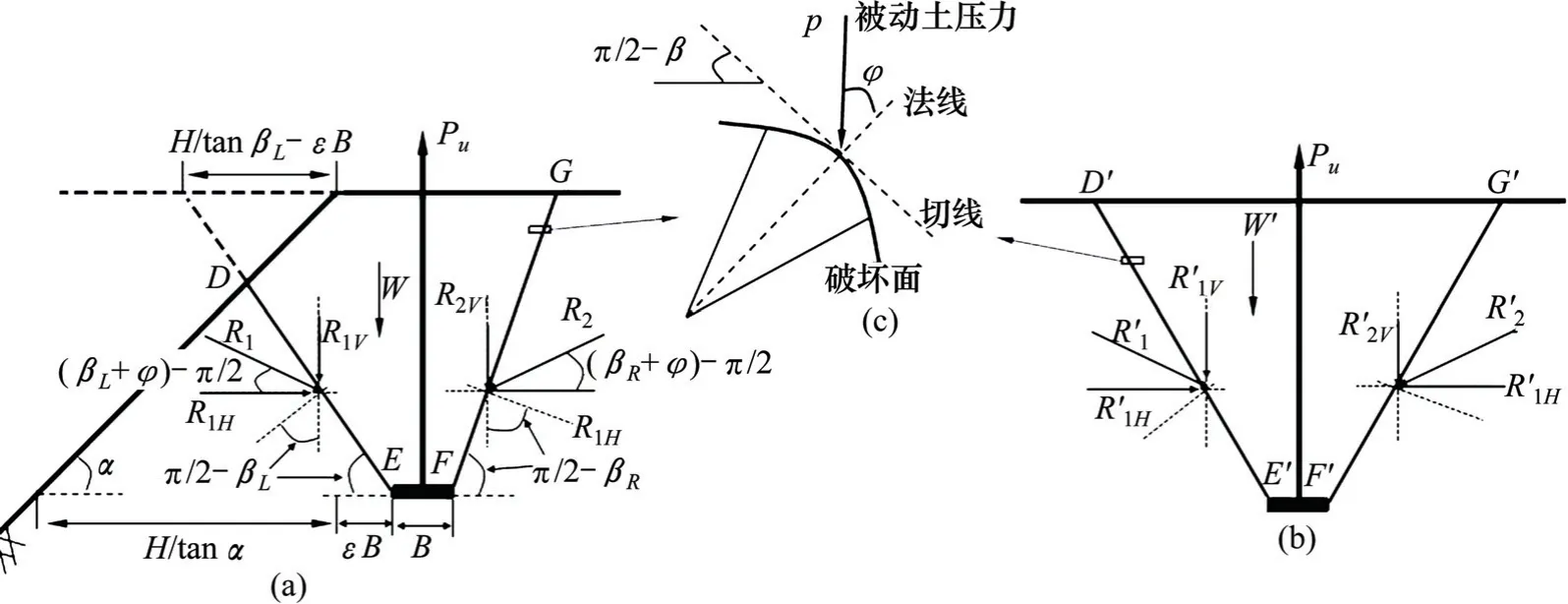
图9 临坡锚板抗拔承载力计算示意图Fig.9 Calculation sketch of uplift capacity of anchor which is adjacent to a slope

4 理论计算公式的验证

4.1 理论与本文试验结果比较

为了验证本文理论模型的合理性及理论计算公式的正确性，现利用该理论公式对本文开展的12组试验锚板的抗拔承载力系数进行估算，将理论与试验的结果进行对比，其对比结果列于表5。经过对比可知，两者结果的最大误差在15%以内，可满足工程需要。

表5 理论公式解与本文试验结果的对比Table 5 Comparison between the proposed theoretical solution and experimental results in this study

4.2 理论与其他文献结果比较

为了进一步验证本文理论模型的合理性及理论计算公式的正确性，本文的理论计算结果也与其他参考文献[13,16-17]计算结果进行了对比。Suits等[17]在研究砂土边坡加筋对锚板抗拔承载力影响的模型试验中开展了7 组临近未加筋砂土边坡条形锚板的抗拔试验，其中边坡角度α=33°，砂土的密实度γ=17.44，18.15 和19.10 kN/m3，其对应的砂土内摩擦角分别为34°，37.5°和43°，锚板的埋置比λ=1，2 和2.5，锚板的临坡比ε=0，1 和2，具体如表6中所示。Ganesh 等[13]通过上限法对Sawwaf 开展的上述模型实验中锚板抗拔承载力进行了理论求解，Khuntia 等[16]通过有限单元法也对这一问题给出了解答。本文收集了这些学者的试验数据或理论解对本文中的理论公式的计算结果进行验证，对比结果如表6所示，本文和Ganesh 及Khuntia 2 位学者的计算结果较为接近，从而也进一步验证了本文公式的合理性。但值得注意的是，Sawwaf 的试验测得的结果要小于Ganesh，Khuntia 和本文的计算结果，其原因是因为Sawwaf 试验过程中锚板发生了旋转，而在理论计算中锚板的旋转位移并没有考虑在内，造成了相应的误差。

表6 理论公式解与其他文献结果的对比(α=33°)Table 6 Comparison between the proposed theoretical solution and results of other literature

5 结论

1)试验结果表明临坡比和边坡角度是影响临坡锚板抗拔承载力重要因素。存在某一临界值，当临坡比增大到该值时，抗拔承载力不再增大而与平地的抗拔承载力相同，此时边坡角度的影响可以忽略。

2)临坡锚板的破坏面形态与平地锚板的不同，锚板两侧的破坏面呈非对称分布，破坏面倾向边坡一侧。当临坡比越小，边坡角度越大，临坡一侧的破坏面与竖直方向的夹角越大，远离边坡一侧的破坏面与竖直方向的夹角越小；随着临坡比增大，边坡角度减小，临坡一侧破坏面的夹角减小，另一侧夹角增大，破坏面开始趋近于平地时的破坏面。

3)根据试验结果，利用极限平衡和Kötter 方程推导得到临坡条形锚板抗拔承载力的理论计算公式，与试验测试结果及前人的研究成果对比，验证了该公式的正确性和实用性，可为实际工程提供参考。