高峰时段城市轨道交通快慢车与多站限流协同优化方法

陈维亚，王婕妤，章雍，康梓轩

(中南大学 交通运输工程学院，湖南 长沙410075)

车站限流和开行快慢车作为城市轨道交通应对供需不均衡压力的重要方式，其主要目的是为了缓解车站客运组织能力、列车服务能力与客流需求的不匹配问题。根据客流分布特征制定科学合理的调整方案不仅能保障客运组织的安全性[1-2]，还有利于提高客运周转效率[3-5]及乘车公平性[6-7]。国内外学者已对车站限流及快慢车方案进行了较多研究。车站限流方面，蒋琦玮等[1]基于城市轨道交通车站空间分区的实时客流数据构建模型决策出车站的三级限流策略，实现车站资源的合理利用。张正等[8]根据流量平衡原理，提出线路上两站同时发生大客流时的协同限流方法。ZHANG 等[2]从网络角度考虑换乘客流对线路影响，研究线网车站间的协调控制方法。快慢车组织方面，万书勤[9]提出由于快慢车的速度差异导致前后车距离不满足安全追踪间隔时，需要考虑快车越行行为的观点。赵欣苗等[3]对比无越行条件和有越行条件下的2 类快慢车模式，指出在相同条件下越行更能适应停站时间的多样性。NIU 等[10]研究针对时变和过饱和客流需求的快慢车开行方案，通过对比快慢车均衡与非均衡2 类发车方式，得到非均衡发车能更好地提高城市轨道交通服务水平的结论。和扬[4]研究高峰时段的快慢车停站方案，以此满足各站乘降量不均衡的客流运输需求。快慢车与车站限流协同方面，JIANG等[6]在不考虑越行的前提下，依据车站进线客流量和出线客流量对车站进行重要度排序，确定大站列车的停站方案，同时对多个车站客流进行协同控制。上述成果为客运组织方案的制定提供了有益借鉴，但研究大多从单一的快慢车角度或者车站协同限流的角度缓解线路客流压力，对于两者组合策略的研究较少。因此，本文以市域线路的高峰客流组织为研究对象，综合考虑快慢车开行方式、列车承载能力和车站乘客安全容量，以提高乘客出行效率和乘车公平性为目标，寻求有越行条件下的多站协调限流和快慢车非均衡发车的协同优化方法。

1 问题描述与模型假设

本文主要研究城市轨道交通市域线路高峰时段快慢车开行方案与多个车站协调限流方案的组合决策问题。

如图1所示，假设线路有4 个车站，列车以一定的顺序和间隔从始发站依次发出，在区间运行、到站停车(跨站或越行)，乘客以一定的规律到达车站进入站台，在列车停站期间完成上下车的交互。因此，在给定研究时段内线路客流OD 的条件下，如何设定体现乘客出行效率与乘车公平性的目标以决策出快车跨站及越行站点、快慢车的始发间隔及线路各站的到发时刻、各状态的上车人数是本文主要解决的问题。

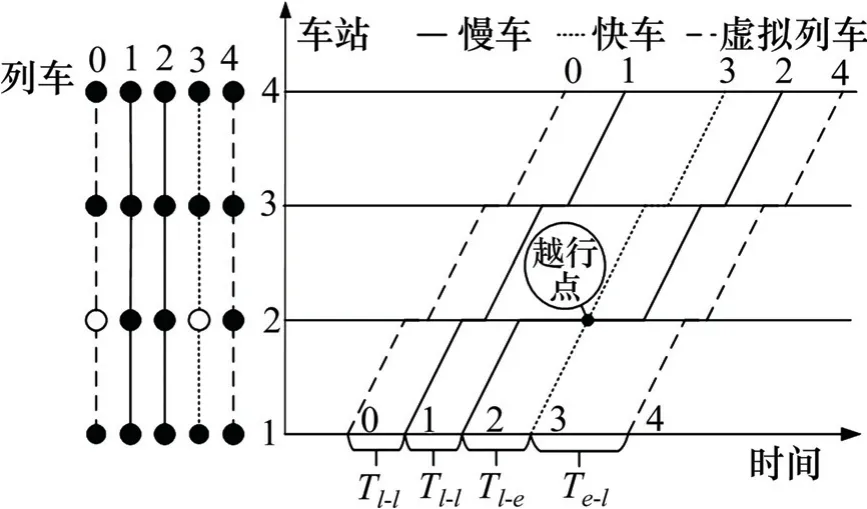
图1 快慢车组织方案示意图Fig.1 Scheme of express/local trains operation with overtaking

所研究问题受多因素影响，因素之间存在复杂的关系。不失一般性和严谨性，对模型做如下简化假设(以图1为例描述)：

1)快慢车开行比例为fe:fl=1:2[4]；快车和慢车的车型、编组均相同，区间巡航速度不存在差异，且均采用大交路。

2)为了减少运营组织的复杂性，快慢车采取非均衡的发车方式[3]且同类列车连续发车，本文将研究时段T划分为以T/fe为粒度的多个细分时段，T/fe内包括2 列慢车和1 列快车，且为慢车、慢车和快车配组开行[4]。

3)轨道交通线路上的车站均具备设置越行线的条件。若存在越行，快车的越行位置为车站，越行方式为不停站越行[3-4]，且每列慢车最多被快车越行1 次，每列快车最多越行慢车1 次。

4)假定各站的乘客均匀连续到达，线路各车站的乘客到达率存在差异[11]。由于可进行多级站控[1]，乘客的到达率假定为乘客的站台到达率。

5)乘客采用一站直达的方式优先选乘先抵达列车，不可直达时选乘慢车，且因不可直达而留乘的乘客最多滞留1 次。

6)以先后离开同一站台n的2 列车的发车间隔作为一个状态 Δtkn，如第3 站列车1 与列车3 之间的发车间隔表示为 Δt33，每个状态内包含站台限流、乘客进站台候车、列车区间运行、列车停靠或跨站、乘客下车、乘客选择、乘客上车、乘客留乘、列车发车等几个行为。状态的更新以各列车的发出作为触发点，且更新对象仅为该状态内的列车和列车停靠或经过的站台。

7)研究时段仅为高峰小时，考虑到客流的连续性，在时段始末分别设置2 趟虚拟慢车(如列车1与列车4)，用以计算和修正研究时段前后乘客的出行时间。

2 建模

2.1 符号及变量说明

k为列车的车次号，k∈1,2,3,…,K+1；

n为车站编号，n,m∈1,2,3,…,N；

fl和fe分别为慢车和快车的发车频率；

s为慢车初始停站时间；

tsk.n为列车k在n站的实际停站时间；

α和β分别为列车的起、停附加时间；

hmin为最小追踪间隔；

为列车k到达n站乘客下车后的站台剩余安全容量；

为列车k到达n站乘客下车后列车剩余承载能力；

为 Δtkn内乘客对列车k完成快慢车选择的实际上车需求；

trk.n为列车k在区间(n～n+1)的运行时分；

为状态 Δtkn内新到达的乘客数量；

为状态 Δtkn结束站台外的限流数量；

为状态 Δtkn结束站台留乘乘客数量；

为列车k离开n站时的在车人数；

为状态 Δtkn内的下车人数；

为状态 Δtkn内的总候车人数；

为决策变量，表示状态 Δtkn内的上车人数；

un为0-1 变量，表示快车的停站序列，停站取1，否则取0；

ok,n为0-1 变量，表示越行位置，列车k在n站越行取1，否则取0；

Tl-l，Tl-e和Te-l均为决策变量，分别表示连续2列慢车、前慢后快以及前快后慢的2 列车在首站的发车间隔；

tak,n和tdk,n均为决策变量，分别表示列车k在n站的到达和发车时刻；

ekn为列车k在离开n站时前一趟离开的列车车次号；

Dnj和Anj分别为在n站第j趟发车和到达的列车车次号，其中j表示顺序编号；

zkn为列车k在n站的离开顺序；

ekn，Dnj和zkn三者的关系可表示为：

Δtkn为列车k与列车ekn在n站的发车间隔，表示状态，可表示为：

2.2 目标函数

以提高乘客出行效率和乘车公平性为出发点设立目标函数。由于快车的跨站和越行是节省快车乘客在车旅行时间、延长慢车乘客在站和在车等待时间的关键影响因素，可用最小化线路乘客总体出行时间作为目标提高乘客出行效率[3-5]。乘车的不公平主要是由于列车对线路各站的服务存在先后顺序，高峰小时当上游车站的乘客上车人数过多，列车承载能力处于饱和状态后，下游车站会出现滞留乘客较多、滞留时间较长的现象。因此，可用最小化各站各状态内上车人数占总候车人数的比例方差之和作为目标提高乘车公平性[6-7,12]。

2.2.1 最小化线路乘客总出行时间

以线路乘客的总出行时间作为乘客出行效率的效果评价指标，线路乘客总出行时间越少，说明乘客的出行效率越高。乘客总出行时间T1(总客流量×平均等待时间)包括乘客在站总等待时间Tw和乘客在车总旅行时间To2 部分。最小化线路上所有乘客总出行时间的目标函数如式(3)所示：

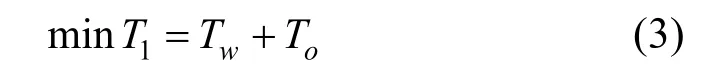
1)乘客在站总等待时间Tw

每个状态的总候车乘客由该状态新到达的乘客、该站上一状态的滞留乘客(站台留乘乘客和站台外限流乘客)组成。乘客的在站等待时间可根据乘客的类型分为新到达乘客的在站等待时间和滞留乘客的在站等待时间2 类。同一状态的新到达乘客的平均等待时间趋近于发车间隔的一半[13]，滞留乘客的平均等待时间为完整的发车间隔。

n站上一状态结束的滞留乘客在状态内的总在站等待时间如式(5)所示：

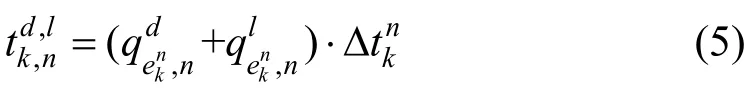
乘客的在站总等待时间如式(6)表示：

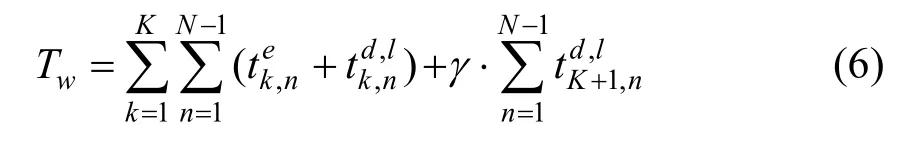
式中：γ为搭乘虚拟列车滞留乘客的出行时间惩罚系数，取值为研究时段结束所有车站滞留人数之和与列车最大承载能力的比值。

2)乘客在车总旅行时间To

乘客在车旅行时间是指从乘客完成登乘列车至到达目的车站后下车所耗费的时间。根据列车在线路上的运行过程，将同一列车在相邻车站(n～n+1)的发车间隔作为时段划分，乘客的在车旅行时间细化为2 类：区间旅行时间以及在站停靠时间。

登乘列车k的乘客在区间(n～n+1)的总旅行时间如式(7)所示：

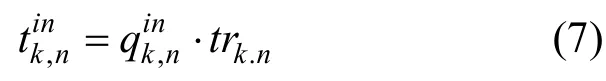
登乘列车k的乘客在车站n+1 的总停靠时间如式(8)所示：

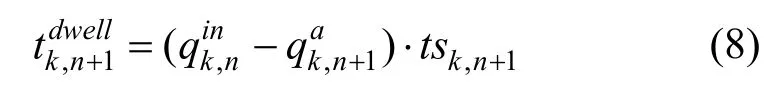
乘客在线路的总旅行时间如式(9)所示：

2.2.2 最小化各站各状态内上车人数占总候车人数的比例方差之和

从列车运力分配的公平性角度，引入各站各状态内上车人数与总候车人数的比例方差之和最小(如式(10)所示)作为列车服务线路各站公平程度的衡量标准。方差之和T2越小，说明各站乘客上车比例越均衡，协同性越高。

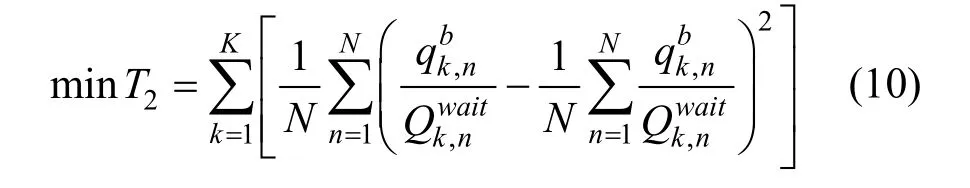
2.3 约束条件

2.3.1 快车跨站约束

快车跨站位置的选择需要满足3 个要求：一是由于快慢车采取大交路，要求快车在线路的首末站必须停车(式(11))；二是考虑乘客出行感受，约定快车连续跨站次数不超过2 站(式(12))；三是为体现快慢车的差异和价值，快车至少跨1 个站(式(13))；

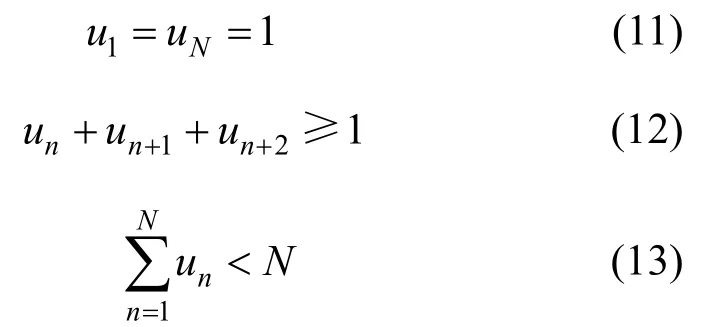
2.3.2 快车越行约束

快车最多越行慢车1 次，慢车最多被快车越行1 次，且越行的方式为跨站越行。

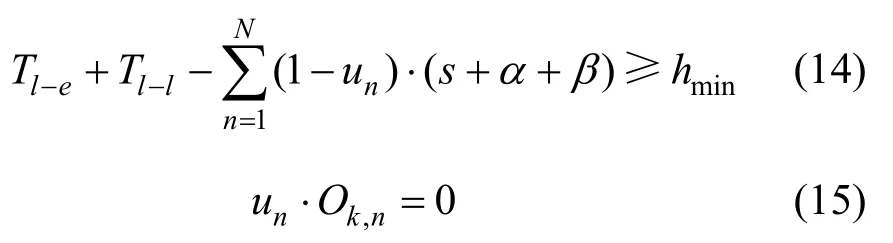
2.3.3 追踪间隔约束

线路上前后列车在各站的到发间隔必须满足最小追踪间隔以保证运行安全，且越行前后列车到发时刻，必须以满足最小追踪间隔为首要原则进行调整。

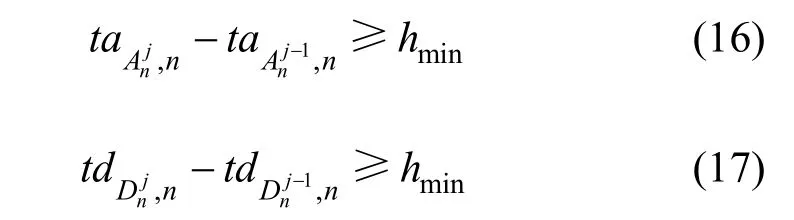
2.3.4 列车和站台能力约束

综合考虑客运组织安全与乘客对快慢车选择所带来的客流需求与上车需求的差异，状态 Δtkn内的上车人数应受到列车承载能力、车站安全容量与乘客的实际上车需求约束。根据假设，状态 Δtekn内的站台留乘乘客在状态 Δtkn内必须全部上车。

3 求解算法

上述模型是一个多目标非线性优化模型，且决策变量中包含了0-1 变量和其他整数变量，不存在多项式求解算法，因此本文设计嵌套混合遗传算法进行求解。外层算法求解快慢车方案，内层算法求解多个车站的协调限流方案，内、外层算法嵌套迭代求出快慢车始发间隔、在线路各站的到发时刻、快车跨站和越行站点、各状态的上车人数。具体算法步骤描述如下。

3.1 外层算法

上述模型对0-1 变量的约束容易判断，因车站数量有限，变量的组合方式有限，其可行解数量有限，故对快慢车方案的初始解采用枚举法列出。具体说明如下。

Step 1：初始化客流OD 等基础数据，根据约束(11)～(13)，枚举un可能的所有方式(用二进制表示un)并编号，记总数量为L。

Step 2：令l=1。

Step 3：令Tl-l=T/3fe。

Step 4：令Tl-e=T/fe-Tl-l-hmin；Te-l=T/fe-Tl-l-Tl-e。

Step 5：依据列车的运行过程[3-4]，生成该Tl-e的开行方案。判断新生成的开行方案是否满足约束(14)～(17)，若满足，将可行开行方案记为ul，作为初始解跳转输入至内层算法；否则令Tl-e=Tl-e-1，重复Step 5。

Step 6：将返回的Fitness-ul-best存于Fitnes-best矩阵中，判断Tl-e=hmin是否成立，若成立，跳转至Step 7，否则令Tl-e=Tl-e-1，跳转至Step 5。

Step 7：判断l=L是否成立：若成立，比较Fitnesbest内所有的适应度值，其最优元素Fitnes-all-best作为外层算法的最优解输出；否则令l=l+1，跳转至Step 3。

3.2 内层算法

Step 1：参数初始化。确定内层算法染色体的初始种群、最大迭代次数、染色体交叉概率和变异概率。

Step 2：编码开行方案。将外层输出的开行方案ul作为执行内层染色体编码的初始数据，内层染色体为各状态上车人数，釆用实数编码，大小为(K×N)的编码矩阵，其中位于(3×4)位置的基因代表车站4 第3 趟(j=3)离开列车的上车人数。

Step 3：初始化父代种群。种群内的每个初始解在满足式(18)的条件下，从下标和最小的变量开始依次循环生成。

Step 4：确定适应度函数。2 个目标函数的计算单位不同，通过归一化对目标函数进行无量纲处理，对2 个目标函数进行线性加权得到适应度函数。2 目标函数的重要程度采用权重系数ω1和ω2来体现，且ω1+ω2=1。

Step 5：选择操作。采用轮赌盘方式。按最优保存策略将部分个体直接遗传至下一代。

Step 6：交叉变异操作。采用均匀交叉策略和区间随机数的变异策略，对不满足约束(18)的染色体进行修正，获得子代个体，形成新的种群，存于Fitness-ul矩阵中。

Step 7：循环执行Step 4 和Step 6，直到达到最大迭代次数。

Step 8：比较Fitness-ul内所有的适应度值，以最优Fitness-ul-best作为开行方案ul的最优解，将Fitness-ul-best的组合方案返回至外层算法Step 6，内层算法结束。

4 算例分析

4.1 算例描述

以某市域轨道交通线路为背景构造算例。线路共12 个车站，各站站台安全容量如表1所示。

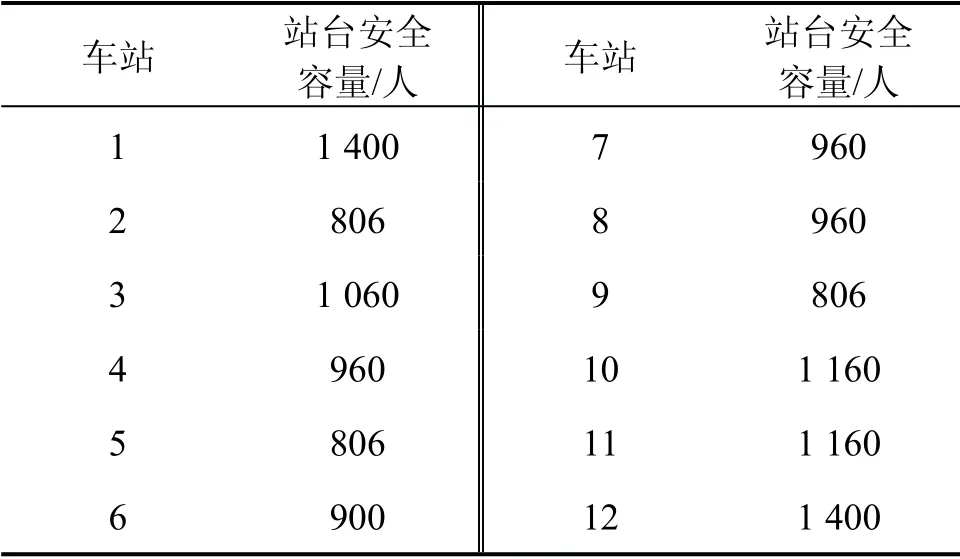
表1 站台安全容量Table 1 Safety capacity of each station platform

总里程为27.02 km，列车区间巡航速度为80 km/h，区间长度如表2所示。车站均预留了越行配线，起、停附加时间α=β=14 s，慢车初始停站时间s=45 s，最小追踪间隔时间hmin=120 s，受设施设备限制，最大列车开行频率为18 列/h。列车最大承载能力Qc=1 762 人。

研究时段为早高峰07:30～08:30，仅考虑上行方向，客流OD 如表3所示：该线路乘客的上车需求沿列车开行方向逐步递减，乘客的下车需求沿列车开行方向逐步递增。

表2 线路区间长度Table 2 Length of each interval

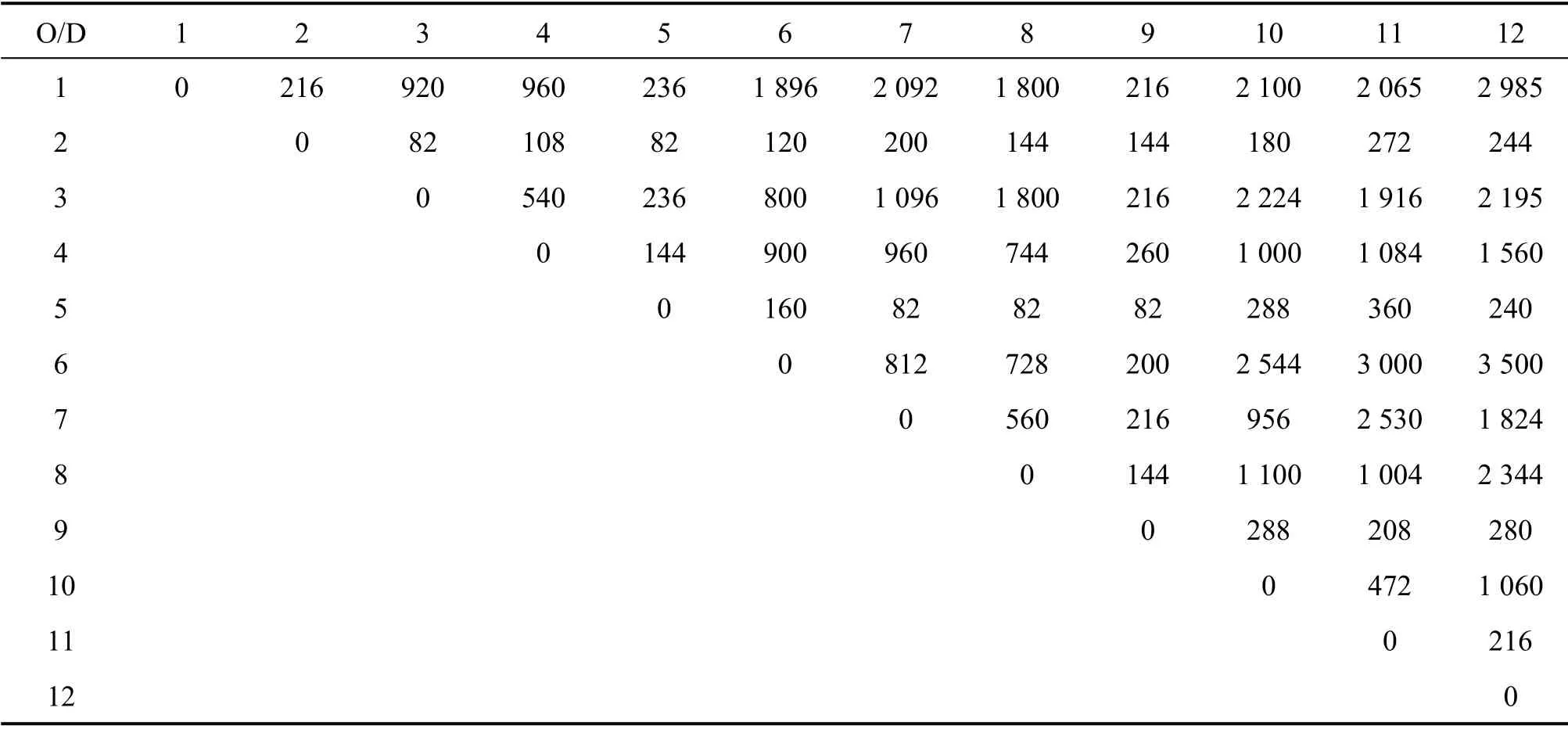
表3 高峰小时线路单向OD 客流Table 3 Passenger OD in one direction in the peak hour

4.2 实验方案与结果

遗传算法中设定初始种群M=300，最大迭代次数C=1 000，交叉概率Pc=0.90，变异概率Pm=0.20，考虑大客流时提高乘客的出行效率更为重要，设2个目标函数权重ω1=0.8，ω2=0.2。

利用MATLAB 语言实现算法，迭代1 000 次的适应度函数值为0.026 6，符合预期终止条件。生成的快慢车停站方案如图2所示：在研究时段内，快慢车以1:2 的比例从首站发车，发车频率分别为6列/h 和 12 列/h 。快车的停站方案un为10 110 111 111，即在第2 和第5 站跨站，第2 站越行。始发站发车间隔Tl-l，Tl-e和Te-l分别为200，134和266 s。结果与文献[3-4]的实验效果一致，快慢车方案的跨站和越行位置均选择在乘客乘降量较小的车站，说明该快慢车方案与客流的分布特征相匹配，具有一定的适用性。

图2 快慢车运行计划图Fig.2 Time-space schedule of the express/local train

各站上车的比例方差之和为0.289 7，由上车人数转换得到最佳进站人数如表4所示。

表4 各状态的最佳进站人数Table 4 Best incoming passenger flow in each state

根据客流OD 分布可知：研究时段的列车运输能力远不能满足线路的客流总需求，尤其在第1，3和6 站的客流需求较大，供需匹配矛盾较为突出，因此，在这3 站必须要加大限流力度以确保站台及列车上乘客的出行安全和车站间的上车均衡。对于乘降量稍小的第2，4 和5 站也进行了部分限流，目的是为其下游车站预留更多的列车运输能力。在第7 站之后，车站的限流力度逐渐减小，其主要原因是因为第7 站后的下车人数多于上车人数，供需匹配矛盾大幅度减小。

在列车发车总频次为18 列/h 的情况下，以现有的目标函数及其权重，计算对比站站停方案与本文提出的快慢车方案的开行效果，如表5所示。

表5 快慢车方案与站站停方案效果对比Table 5 Effect comparison between express/local trains and only local trains

2 方案的输送能力相当，说明快慢车越行方案相比站站停方案并没有导致列车的运输能力降低。对比乘客总出行时间，开行快慢车比站站停方案节省了1 313 h，主要原因是第2 和第5 站的乘降量较小且其上游车站的上车人数较多，快车的跨站及越行行为引发的在站乘客的候车时间延误相对于快车乘客节省的在车旅行时间较少，相对站站停方案，总体出行时间得到了优化。

4.3 敏感性分析

考虑到2 目标函数之间的相互制约关系，本文通过10 次独立实验，对比不同权重系数对方案的影响。图3给出了权重系数ω1由0.1 增加到0.9 时，乘客总出行时间的变化趋势，图4给出了无车站协调限流以及权重系数ω2为0.2，0.5 和0.9 时各站平均滞留人数。

由图3可知：随ω1不断增加，乘客总出行时间递减，尤其ω1=0.1 时，T1=166 938 h，ω1=0.9 时，T1=44 695 h，二者相差很大。

由图4可知：在不考虑各站协调限流时，第6站的平均滞留人数比例很高，这是因为列车按照运行先后顺序依次服务线路各车站的乘客，位于靠前车站(第1 和3 站)的乘客更多被带走，列车剩余运输能力变小，后续车站尤其第6 站的乘客登乘量减少，滞留乘客累积越来越多，客流组织压力增大的同时后续车站的乘客公平性受到影响；反观考虑车站协调限流的方案，随着ω2增大，各站平均滞留人数比趋于均衡，尤其第1，3 和6 大客流站的平均滞留乘客比越均衡，说明优化目标在运力调配公平性上发挥了作用。

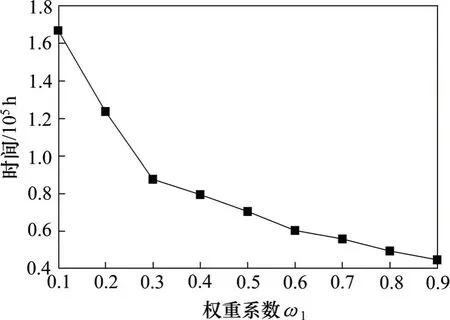
图3 乘客总出行时间比较Fig.3 Comparison of passengers’total travel time at stations

图4 车站平均滞留人次比较Fig.4 Comparison of the average number of detainees

2 目标随权重系数的改变大致成反向变化，且在2 目标函数的权重系数取两端值时效果差异较大，说明2 目标函数之间存在博弈关系，比如更多考虑乘客出行公平性时，一定程度上则会降低乘客的总体出行效率。由此可知，权重系数的变化会导致客流控制目标产生差异，在实际应用时需根据客流分布以及运营目标合理设置两者的权重。

5 结论

1)相比站站停方案，根据线路的客流分布特征合理制定快慢车方案在一定程度上能节省乘客的总出行时间，能提高乘客出行效率。

2)考虑多车站协调限流可以提高乘客乘车的公平性，同时降低大客流车站的客运组织安全风险。

3)权重系数的变化会导致客流控制目标值产生差异，在实际应用时需要根据线路客流分布特征和运营目标进行合理设置。