斜坡浅埋水平条形锚板抗拔承载力的极限分析

黄明华，李 盾，李嘉成

(湖南大学岩土工程研究所，湖南 长沙 410082)

锚板是一种重要的抗拔基础型式，在高层建筑结构、高耸构筑物、输电线塔/通讯塔、边坡挡土墙等工程领域中得到了广泛的应用[1-8]。实际工程应用的锚板种类繁多，按照形状可分为条形锚板、圆形锚板和矩形锚板；按照埋深可分为浅埋锚板和深埋锚板；按照埋设方式可分为水平锚板、垂直锚板和倾斜锚板。具体研究时，通常可将不同形状的锚板简化为条形锚板，按照平面应变问题进行分析[2-3]。因此，条形锚板抗拔承载特性的研究具有重要工程意义。

长期以来，条形锚板抗拔承载特性是岩土工程领域的研究重点之一。特别是最为典型的浅埋锚板，众多学者对其抗拔承载力与破裂机制开展了较为广泛的研究。何思明[1]基于试验结果研究了长方形、圆形和条形锚板的抗拔破裂面型式及其承载力；王洪涛等[2]基于非线性Mohr-Coulomb准则及其关联流动法则，采用极限分析和变分原理获得了浅埋条形锚板的抗拔承载力和破裂机制；茜平一等[4]基于原型和模型试验结果，较为系统地分析了浅埋锚板周边土体的破坏过程与特征；胡伟等[5]基于自主研制的条形锚板水平拉拔可视化模型试验以及数值模拟试验，研究了拉拔过程中锚板板前土体的位移变形规律；许华青等[6]采用PIV技术对粉土中锚板的抗拔承载特性进行了室内模型试验研究；Kumar等[7-8]采用多块体上限法对浅埋锚板的抗拔承载特性进行了分析，基于该方法，黄茂松等[9]分析了砂土中条形锚板的抗拔承载力；赵练恒等[10]采用上限法求解了浅埋法向受力倾斜条形锚板的抗拔承载力；张晓曦等[11]采用水平条分法与极限平衡原理分析了倾斜荷载作用下条形锚板的破裂面和抗拔承载特性；黄明华等[12]采用上限法分析了土体非均质和非线性强度特性对浅埋条形锚板抗拔承载力的影响；Merifield等[13-14]基于极限分析有限元法分析了条形锚板的抗拔承载特性。分析可见，上述研究均假设锚板埋设于水平地表土层之中，对斜坡锚板抗拔承载力的研究和探讨很少涉及。

实际工程中，在山区和丘陵等复杂地形区域，输电线塔、通讯塔、边坡挡土墙等工程结构经常需要建造在斜坡地形上。因此，对斜坡锚板抗拔承载特性展开研究具有重要的工程意义。在这方面，余生兵等[3]基于组合块体集和极限分析方法，初步分析了斜坡浅埋条形锚板的抗拔承载特性；但该方法速度场、内能耗散和外力做功等需采用多个基本块体叠加而成，计算方法较为繁琐。鉴于此，借鉴文献[2,15]的分析方法和思路，本文拟对斜坡浅埋水平条形锚板的抗拔承载力及其上方土体破裂机制进行研究，并分析斜坡倾角和锚板埋深对锚板抗拔承载力的影响，以期为斜坡锚板基础设计提供一定理论参考。

1 曲线破坏机构与非线性强度准则

已有研究表明[1-5,13-16]，在一定岩土介质条件下，随着锚板埋深率(埋深与宽度之比)的增加，其抗拔承载力逐渐增大；当埋深率增加到某一临界值(即临界埋深率)，锚板抗拔承载力增加明显趋于平缓。以临界埋深率为界定标准，锚板可以区分为浅埋锚板和深埋锚板。目前，国内外对于锚板临界埋深率的取值尚未形成统一的认识[5]。谭亦高等[16]指出：对于松散岩土体，锚板埋深率小于4～6时，可以界定为浅埋锚板；对于密实岩土体，锚板埋深率小于7～9时，可以界定为浅埋锚板。除了埋深率不同之外，浅埋锚板和深埋锚板最为根本的区别是其破坏形式有所差异。在上拔荷载作用下，深埋锚板呈现局部破坏模式，破裂面则不能延伸到土体表面；而浅埋锚板的破裂面则从锚板边缘一直延伸到土体表面。

目前，关于锚板破裂面形状的假设较多。为便于斜坡浅埋水平条形锚板抗拔承载力的计算，根据极限分析上限定理以及文献[2,15]的相关研究成果，假设锚板为刚性体，且锚板与周边土体不产生相对滑动，构造出斜坡浅埋水平条形锚板在极限状态下的曲线型破坏机构，如图1所示。其中，斜坡倾角为α，锚板宽度为B，平均埋深为H，土体重度为γ。建立以锚板上表面中心为原点O、x轴以向右为正、z轴以向上为正的直角坐标系，假设锚板上方两侧土体破裂分离曲面所对应的方程分别为fL(-x)和fR(x)，二者在坡面处的水平破裂宽度分别为xL和xR。为了便于推导和分析，图1中给出了锚板上方左侧土体破裂面及斜坡坡面关于z轴的镜像与对应方程。

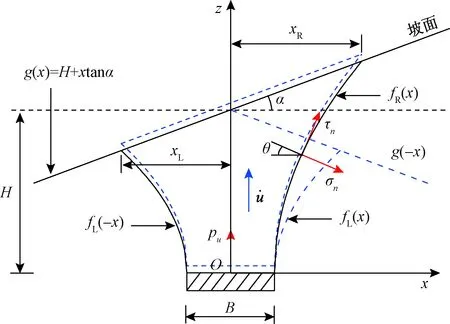
图1 斜坡浅埋水平条形锚板破坏机构Fig.1 Failure mechanism of the shallow horizontal strip anchor plate embedded in slope

同时，为有效反映锚板上方土体的强度特性，采用形式简单、应用广泛的非线性Mohr-Coulomb强度准则来刻画极限状态下锚板上方土体达到破坏时的剪应力与正应力关系[17-19]，即：

τn=c0(1+σn/σt)1/m,m≥1

(1)

式中：τn、σn——锚板上方土体破裂面上的剪应力和正应力；

c0、σt、m——锚板上方土体的初始黏聚力、单轴抗拉强度和无量纲非线性系数。

当m=1时，式(1)变为线性Mohr-Coulomb强度准则。

2 抗拔承载力极限分析与计算方法

2.1 曲线型破坏机构内能耗散功率

对于水平地表条件下的锚板，由于其上方土体的破坏机构具有对称性，仅需计算一侧破坏机构的内能耗散功率；对于斜坡锚板，其上方两侧土体的破坏机构不再具有对称性，二者的内能耗散攻率需要分别进行计算。

(2)

(3)

对应地，左右两侧破坏机构上的单位体积能量耗散功率可以分别表示为[2,15]：

(4)

(5)

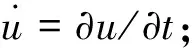
将式(4)和(5)分别沿着左侧和右侧破裂面进行积分，即可获得左侧和右侧破裂面的能量耗散功率，分别为：

(6)

(7)

(8)

2.2 锚板所受外力做功功率

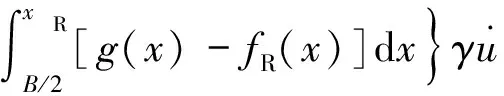
(9)

(10)

2.3 锚板抗拔承载力极限分析

根据虚功功率原理，锚板上方土体破裂面的内能耗散功率应等于其所受外力的做功功率，即：

(11)

将式(7)～(10)代入式(11)中，整理得到斜坡浅埋水平条形锚板的抗拔承载力pu为：

(12)

式中：ΛL(·)、ΛR(·)——两个泛函，具体表达为：

(13)

(14)

根据极限分析的上限定理，对于满足机动允许的任意速度场，由虚功功率方程确定的荷载(式12)应大于或等于锚板的真实极限抗拔力，意味着真实的速度场所确定的荷载必须为最小。因此，要获得锚板的抗拔承载力，必须寻求式(12)在对应区间上的最小值。

式(12)表明，锚板抗拔承载力的极值完全由两个积分型泛函ΛL(·)和ΛR(·)所确定。根据变分原理和欧拉-拉格朗日极值条件，得到：

(15)

(16)

将式(13)和(14)代入式(15)和(16)中，得到：

(17)

(18)

上述两个方程为常系数二阶线性齐次微分方程。对两个方程进行两次积分，得到斜坡锚板上方左右两侧土体破裂面的控制方程，分别为：

(19)

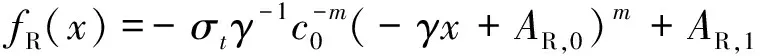
(20)

式中：AL,0、AL,1、AR,0、AR,1——四个积分常数，由边界条件确定。

将式(19)和(20)代入式(12)中，即可获得斜坡浅埋水平条形锚板的抗拔承载力pu为：

pu=pu,L+pu,R

(21)

其中，

(-γxL+AL,0)m+1]+(xL-B/2)[σt+

γ(H-AL,1)-1/2γ(xL+B/2)tanα]

(22)

(-γxR+AR,0)m+1]+(xR-B/2) [σt+

γ(H-AR,1)+1/2γ(xR+B/2)tanα

(23)

2.4 锚板抗拔承载力计算方法

式(21)～(23)中含有4个积分常数和2个待定参数(xL和xR)，需要联合斜坡表面边界条件以及破裂面几何形状进行确定。假设斜坡表面没有受到切向力的作用，则可在斜坡表面选取微元体进行受力分析。根据xL和xR处微元体在斜坡方向的力学平衡条件，可得：

τncos[2(θL+α)]-1/2σnsin[2(θL+α)]=0

(24)

τncos[2(θR-α)]-1/2σnsin[2(θR-α)]=0

(25)

其中，

此外，锚板上方两侧土体破裂面方程fL(x)和fR(x)在其各自的两个端点上，满足边界条件：

fL(B/2)=0,fR(B/2)=0

(26)

fL(xL)=H-xLtanα,fR(xR)=H+xRtanα

(27)

由上述两式可以得到：

(28)

(29)

(30)

(31)

将式(1)、(2)、(19)、(28)和(30)代入式(24)中，可得到一个关于xL的代数方程；同样地，将(1)、(3)、(20)、(29)和(31)代入式(25)中，可得到一个关于xR的代数方程。这两个方程在一般情况(α≠0或m≠1)下均为非线性代数方程，可以采用牛顿迭代法等方法进行求解。

上述分析表明，除斜坡、锚板及土体相关参数(α、B、H、γ、c0、σt和m)为已知量外，锚板抗拔承载力还与待定参数xL和xR有关。其中，xL和xR需要满足对应的非线性代数方程(即约束条件)。由此可见，锚板抗拔承载力(式)的计算问题可以转化为寻求两个目标函数puL(xL)和puR(xR)在相应约束条件下的最小值问题。对于该问题，本文利用序列二次规划方法及MATLAB优化工具箱进行求解[20]。当α=0时，上述积分常数和待定参数存在解析解，具体表达式分别为：

(32)

将式(32)代入式(21)中，得到：

pu=2γxLH+σt(2xL-B)-2(m+1)-1·

(33)

式(33)即为平地条件下浅埋水平条形锚板的抗拔承载力计算公式，其与文献[2]得到的结果一致。可见，文献[2]给出的锚板抗拔承载力计算公式是本文一个特例，同时也验证了本文方法与推导过程的有效性。

3 斜坡锚板抗拔承载力计算与分析

式(21)表明，斜坡浅埋条形锚板的抗拔承载力与斜坡倾角、锚板埋深和宽度以及土体参数有关。限于篇幅，本文主要聚焦斜坡倾角和锚板埋深对斜坡浅埋锚板抗拔承载力的影响，锚板宽度与土体参数的影响则可以借鉴平地锚板抗拔承载力方面的已有研究成果。参考文献[2]的分析参数，选取土体初始黏聚力为15 kPa、单轴抗拉强度为25 kPa、无量纲非线性系数为2.0、重度为18 kN/m3以及锚板宽度为1.5 m，分别计算斜坡倾角为0°～60°、锚板埋深率H/B为1～7时锚板的抗拔承载力及其上方土体的破裂面形状，以分析斜坡倾角和锚板埋深的影响。

3.1 斜坡倾角对锚板抗拔承载力的影响

取锚板埋深率H/B为2，4，6，图2给出了不同倾角条件下斜坡浅埋水平条形锚板的抗拔承载力及其损失率和承担比例。可以看出，其他参数一定时，随着倾角的增大，斜坡锚板的抗拔承载力逐渐减小，且锚板上方左右(下坡、上坡)两侧土体重力及破裂面分担的抗拔承载力比例逐渐产生差异：左侧土体重力及破裂面所承担的抗拔承载力比例随着斜坡倾角的增大而逐渐减小，而右侧土体重力及破裂面所承担的抗拔承载力比例则随着斜坡倾角的增大而逐渐增大。在整体上，锚板承载力的损失率随着斜坡倾角的增大而逐渐非线性增加；斜坡倾角越大，损失率的增加速率也越大。同时，锚板埋深率(H/B)越小，在相同倾角条件下，其左右两侧土体重力及破裂面分担的抗拔承载力比例存在的差异越大，抗拔承载力损失率也越大，意味着斜坡倾角(工程切坡幅度)对埋深较小锚板的抗拔承载力影响更大。

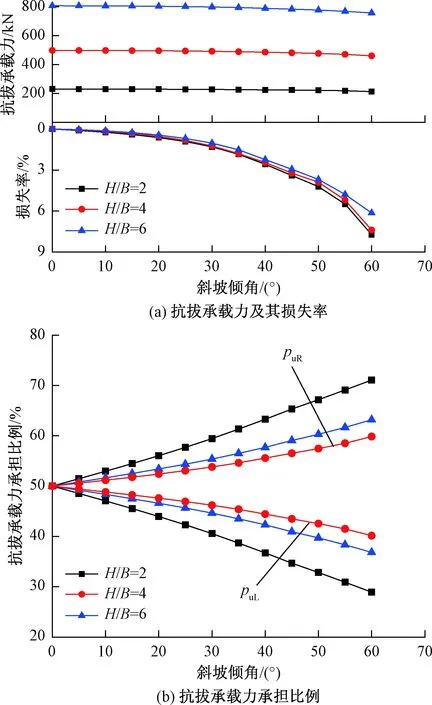
图2 不同倾角条件下斜坡锚板抗拔承载特性Fig.2 Pullout capacity of the shallow horizontal strip anchor plate embedded in slope with different inclination angles

取锚板埋深率H/B为4，图3给出了不同倾角条件下斜坡浅埋水平条形锚板上方土体的破裂面形状。可以看出，对于平地(α=0)浅埋锚板，其上方两侧土体破裂面呈对称的喇叭形分布，与已有试验研究和理论分析成果一致[1-10]；随着斜坡倾角的增大，锚板上方两侧土体破裂面不再具有对称性，左侧(下坡)土体破裂面与竖直方向的夹角逐渐增大，而右侧(上坡)土体破裂面与竖直方向的夹角则逐渐减小；整体上，锚板上方土体破裂面向约束较弱的左侧偏移，这一现象与文献[3]采用组合块体集方法得到的结论一致。

图3 不同倾角条件下斜坡锚板破裂面形状Fig.3 Failure plane shape of the shallow horizontal strip anchor plate embedded in slope with different inclination angles

3.2 锚板埋深对锚板抗拔承载力的影响

取斜坡倾角α为0°、15°、30°和45°，图4给出了不同埋深率(H/B)条件下斜坡浅埋水平条形锚板的抗拔承载力及其承担比例。可以看出，其他参数固定时，随着埋深率的增大，斜坡浅埋锚板的抗拔承载力逐渐增加；在埋深率较小(H/B≤2.0)时，不同斜坡倾角条件下，锚板的抗拔承载力存在较为明显的差异，即斜坡倾角越大，抗拔承载力越小；随着埋深率的增加，斜坡倾角对锚板抗拔承载力的影响逐渐减小。图4(b)表明，埋深率较小时，锚板上方左右(下坡、上坡)两侧土体重力及破裂面分担的抗拔承载力比例存在很大差异，且差异随着斜坡倾角的增大而逐渐明显；随着埋深率的增加，左侧(下坡)土体重力及破裂面分担的抗拔承载力比例逐渐上升，而右侧(上坡)土体重力及破裂面分担的抗拔承载力比例则逐渐下降，且二者分担比例逐渐趋于某一定值。可见，随着埋深的增大，斜坡锚板两侧土体各自所发挥的作用逐渐趋于稳定，即该作用存在一定深度效应。

图4 不同埋深条件下斜坡锚板抗拔承载特性Fig.4 Pullout capacity of the shallow horizontal strip anchor plate in slope with different embedded depths

取斜坡倾角α=30o，缓制不同埋深率条件下斜坡浅埋水平条形锚板上方土体的破裂面形状(图5)。可以看出，随着埋深率的增大，锚板上方两侧土体破裂面开裂宽度逐渐增加；由于左侧(下坡)土体在锚板竖向荷载作用下所受到的侧向约束较小，其破裂面开裂宽度的增加幅度较右侧(上坡)大，以致破裂面在整体上向左侧偏移。

图5 不同埋深条件下斜坡锚板破裂面形状Fig.5 Failure plane shape of the shallow horizontal strip anchor plate in slope with different embedded depths

4 结论

(1)随着斜坡倾角的增大，锚板下坡侧的土体及破裂面所承担抗拔承载力逐渐减小，上坡侧的土体及破裂面所承担抗拔承载力有所增加，但其抗拔承载力整体上呈非线性减小的趋势。

(2)随着斜坡倾角的增大，锚板上方两侧土体破裂面不再具有对称性，下坡侧的土体破裂面与竖直方向的夹角逐渐增大，而上坡侧的土体破裂面与竖直方向的夹角则逐渐减小；整体上，锚板上方土体破裂面向约束较弱的下坡侧偏移。

(3)随着埋深率的增大，锚板上方两侧土体破裂面的开裂宽度逐渐增加，其抗拔承载力亦逐渐增大。埋深率较小时，锚板上、下坡两侧土体及破裂面所分担的抗拔承载力比例存在明显差异，且斜坡倾角越大，差异越大；但随着埋深率的增加，二者的分担比例逐渐趋于某一定值。