数形结合解决听障生二次函数教学中的问题

罗文璟

一、数形结合思想概述

数形结合就是把抽象的数学语言、数量关系与几何图形、位置关系紧密结合起来，通过“以形助数”或“以数解形”，即抽象思维与形象思维的结合，使复杂问题简单化，抽象问题具体化，从而优化解题途径。

数形结合不仅是一种解题方法，还是一种指导思想，比如在课堂上的多媒体教学，就使得数形结合的思想得到充分展现，这不仅有利于为听障生营造一种良好和活跃的课堂气氛，更有利于激发听障生的学习兴趣，使他们想学好数学，努力学好数学。所以巧妙利用“数形结合”思想，把抽象问题具体化，直观形象化，可以达到事半功倍的解题效果。

二、利用“数形结合”思想，解决二次函数性质问题

在认识和熟悉二次函数知识时，我们都知道自变量x和因变量y的变化是比较抽象的，对于听障生来说更难掌握，而“数”与“形”的结合可以解决这一类内容，将解题的思想过程用图象形象地表达出来。所以，教师在二次函数的性质教学过程中，可以充分利用“数”，去找出一一对应的“形”，具体表现如下。

一是充分利用二次函数图象帮助听障生理解和熟悉二次函数性质。

先让学生动手画出二次函数y=ax2的图象，通过“列表——描点——连线”的步骤，听障生可以从表格中观察数据的变化特点，然后根据表格数据画出图象，将二次函数的所有信息充分展现在图象上，逐步深入探究二次函数的其他相关结论。

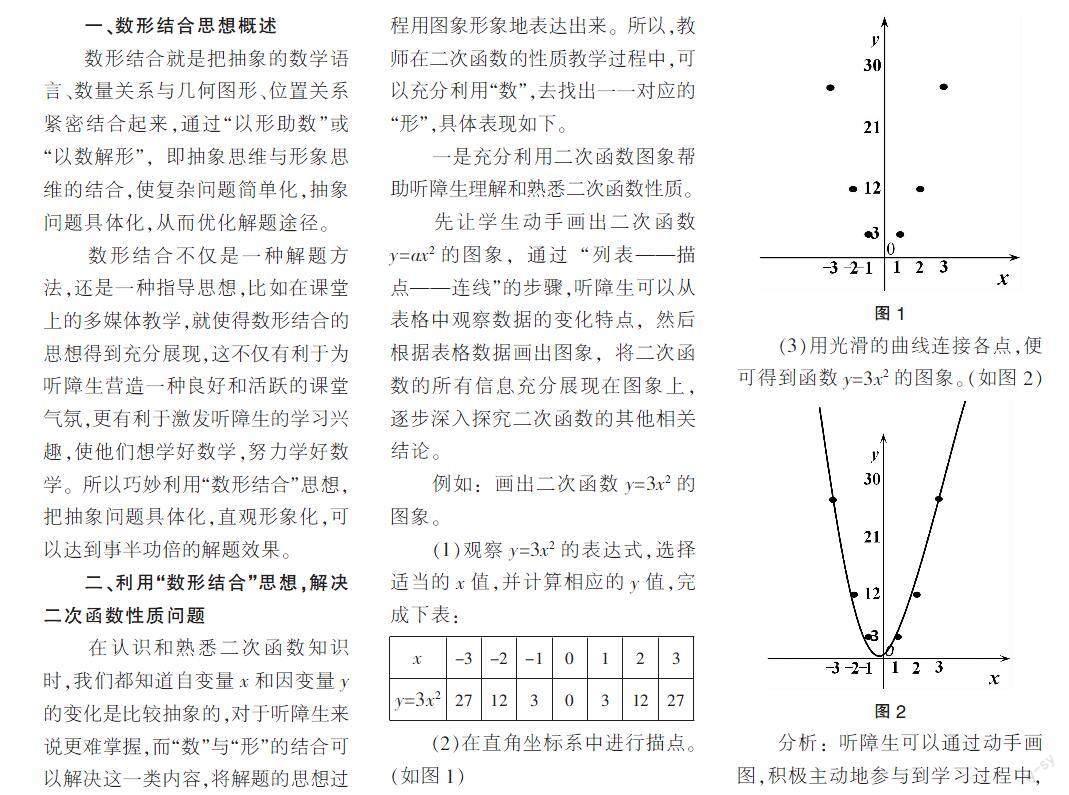
例如：画出二次函数y=3x2的图象。

（1）观察y=3x2的表达式，选择适当的x值，并计算相应的y值，完成下表：

■

（2）在直角坐标系中进行描点。（如图1）

（3）用光滑的曲线连接各点，便可得到函数y=3x2的图象。（如图2）

分析：听障生可以通过动手画图，积极主动地参与到学习过程中，并加深对二次函数性质的理解，充分调动学生的积极性，体现数学活动中充滿未知的探索与创造。

二是教师可以针对此二次函数图象，提出以下四种问题，让学生在小组讨论实践中，检验自己所总结归纳的结论是否正确：（1）是否可以描述该图象的形状？（2）观察图象是否与x轴有交点？如果有，其交点坐标是什么？（3）图象在y轴的左侧和右侧，x的值与y的值进行怎样的变化？（4）此图象是否是轴对称图形，其对称轴是什么？是否有其他方式求其对称轴？通过以上问题归纳总结出二次函数的性质问题，体现了由“数”到 “形”的转变。

三、利用“数形结合”思想，巧解二次函数与一元二次方程之间问题

在初中数学的学习中，我们知道二次函数与一元二次方程有着密不可分的联系，首先从表达式上来看，二次函数表达式为y=ax2+bx+c，而一元二次方程表达式为ax2+bx+c=0，可以看出方程左边式子可以用“y”来替代，我们可以利用一元二次方程ax2+bx+c=0根的个数，来研究二次函数y=ax2+bx+c的图象与x轴的交点个数。

比如一元二次方程ax2+bx+c=0的根有三种情况：有两个不相等的实数根、有两个相等的实数根和没有实数根，根据所学二次函数的知识点，求其图象与x轴交点的横坐标，实质就是求对应的一元二次方程ax2+bx+c=0的根。

因此，通过数形结合思想，来帮助听障生更好地理解一元二次方程根的分布问题，进而得出二次函数图象与x轴交点的个数，接下来，我们通过下面例题来分析一元二次方程根的分布问题来解决二次函数图象问题。

例1.已知方程x2-2ax+a2-1=0在区间（-3，5）上有两根，求实数a的取值范围，并写出二次函数图象与x轴交点的个数。

解：令f（x）= x2-2ax+a2-1=0，如图3所示：

所得充要条件为Δ=（－2a）2－4（a2－1）≥0－30f（-3）=a2+6a+8>0解得：-2

所以实数a的取值范围是    （-2，4），即二次函数图象与x轴交点的个数有两个。

分析：上述题目如果采用求根公式来解出方程的两根，再通过解不等式的取值范围，其计算过程会比较烦琐，会大大降低听障生学习的积极性，而利用二次函数的图象与性质和一元二次方程相关知识来求解，能让听障生更好地理解知识点，熟悉和运用所学的知识点，从而提高解题效率。

四、利用“数形结合”思想，探究求解二次函数在给定区间上的最值问题

二次函数常考的求最值问题题型中，一般式y=ax2+bx+c（a≠0），我们通常采用配方法，将其化为顶点式y=a（x+■）2+■，来获取所求的最值y最值=■，而往往在区间上求最值问题，最可靠的方法，就是利用函数图象与性质，结合其他相关知识，来判断函数的最值问题。因此，教师可以引导学生从题目中获取相关信息，比如自变量x的取值范围、因变量y的取值范围，判断其对称轴分布情况，通过化繁为简，化难为易，最终完成最值问题的解答，我们具体从下面的例题上来分析最值问题：

例2.若f（x）=x2-2x+3，在x∈[a，a+3]上有最小值为g（a），试求   g（a）的表达式．

解：∵f（x）=x2-2x+3= x2-2x+1-1+3=（x-1）2+2

其对称轴为直线x=1，顶点坐标为（1，2）

∴画出其函数图象如图4所示：

①当a+3<1，即a<-2时，g（a）=f（a+3）=a2+4a+6

②当a≤1≤a+3，即-2≤a≤1时，g（a）=f（1）=2

③当a>1时，g（a）= f（a）=a2-2a+3

∴由①②③可知：

g（a）=a2+4a+6（a<－2）2（－2≤a≤1）a2－2a+3（a>1）

分析：根据上述题目解答过程，我们可以看出，通过已知条件，获得“数”的具体信息，听障生可以画出该二次函数的的图象，标明已知信息，再利用对称轴，对比与区间中x的大小关系，达到求二次函数在区间内的最值问题。

责任编辑 李少杰