基于混合整数规划的智能车横纵向一体化滚动优化决策

戴启坤 刘 俊 郭洪艳陈 虹孙 义

(1.吉林大学汽车仿真与控制国家重点实验室,吉林 长春 130022;2.吉林大学通信工程学院,吉林 长春 130022;3.同济大学电子与信息工程学院,上海 201804)

1 引言

智能汽车由于其在保障安全、提高效率等方面的重要潜力,已经成为当前汽车科技革命和产业变革中不可或缺的一部分.决策作为智能汽车中的重要组成部分,主要作用为综合环境及自车信息,使智能汽车产生安全、合理的驾驶行为,指导着智能汽车运动控制系统,对智能汽车的安全性和舒适性有着重要的影响[1].各国推出了多项智能汽车战略,其中都提到了关于决策技术的计划,如:美国在2020年推出的《确保美国在自动车辆技术方面的领先地位: 自动驾驶车辆4.0》中提到“制定智能车辆决策安全性标准”[2];中国同年制定了《智能汽车创新发展战略》,将智能决策控制列为“智能汽车技术创新体系”的一部分[3],由此可见,决策已经成为智能汽车研究中的关键问题.

智能汽车的决策主要有基于规则和基于学习的两种方案.基于规则的方法具体包括基于条件、离散选择、概率模型等方法: 文献[4]将换道决策分为自由、强制和合作换道3类,设计了基于规则的决策方法;文献[5]以换道时间间隙和执行时间为控制量,设计了基于条件触发的变道决策方法,基于条件的决策方法能够实现典型场景下的决策,但由于实际工况众多,基于条件的决策方法难以覆盖所有工况;文献[6]通过设计参考生成器,生成多个参考决策,并根据指标搜索出最优的决策,由于该参考决策的离散性,因此决策难以达到最优,并且存在决策切换造成的系统抖动问题;文献[7]建立一种动态概率网格的行车环境几何模型,计算每个行车单元的占用概率,并输入贝叶斯决策网络,量化输出变道决策期望效用值;文献[8]利用贝叶斯网络评估碰撞的可能性,通过分层状态机得出车辆决策,基于概率的决策方法的可解释性比较强,但描述概率的函数及参数较难选择.

近年来,基于学习的决策也被使用并部分应用于实车上,取得了良好的效果[9]:文献[10]提出了一种基于v–支持向量机的换道决策方法,实现对突发意外障碍车辆的躲避;文献[11]基于真实驾驶数据,训练卷积神经网络,完成对路径的学习;文献[12–13]分别提出了基于深度神经网络和FCN-LSTM网络的端到端的自动驾驶方法,以图像和轨迹为输入,学习驾驶员对车辆的操作,但基于学习的决策十分依赖数据的质量,且可解释性不足;文献[14]基于博弈论对车辆之间的关系建立了模型,使用强化学习训练智能体;文献[15]针对车型、路况等模型误差的问题,提出基于深度强化学习的模型迁移决策方法,基于强化学习的决策方法中,奖励函数经常难以定义或过于复杂,并且对系统约束的处理能力较差.

决策模型描述的是智能车决策到智能车运动的特性,根据待决策量的不同可分为操纵决策模型和行为决策模型.操纵决策模型主要以自动驾驶系统对车辆的控制量为输入: 文献[16]以前轮转角和纵向轮胎力为输入,建立了描述车辆横纵向运动的动力学模型;文献[17]以前轮转角和纵向加速度为输入,建立了非线性的车辆运动学模型;文献[18]建立了以参考预瞄点为输入,车辆运动学信息为状态的类人动力学决策模型.根据操纵决策模型可直接决策出驾驶动作,但由于要描述的对象较为复杂,因此系统阶次较高.

而行为决策模型以车辆的换道和驱制动为模型输入: 文献[19]以换道为动作,以本车所在车道为状态建立了马尔可夫决策模型;文献[20]以纵向加速度和换道动作为输入,建立了混合逻辑的智能车决策模型.在包含感知、决策、规划、控制无人车系统架构中,决策层的任务为像熟练驾驶员一样考虑周围环境,产生安全合理的驾驶行为[1];规划和感知层的主要任务分别为根据决策层输出的行为决策规划参考轨迹和精准跟踪参考轨迹[9].

由于模型预测控制(model predictive control,MPC)能显式处理约束,适合处理实际决策中车辆位置、速度、安全性等约束;且具有预测的功能,能较好利用感知部分输出的周车预测行为.因此,本文提出了一种基于混合整数规划的智能车横纵向一体化滚动优化决策方法: 首先,建立了控制量混合整数的智能车决策模型;然后,设计了横纵向一体化滚动优化决策算法并给出了优化问题递归可行性的证明;最后,基于veDYNA和simulink联合仿真及实车试验对决策算法有效性进行了验证.

本文的主要贡献在于: 1)综合车辆实际换道轨迹的采集与分析,将车辆换道轨迹描述为换道动作和车辆位置的一阶惯性环节,建立了混合整数智能车决策模型,简化地描述了智能车的行为决策过程;2)针对横纵向联合决策问题,建立了适用于弯道的智能车辆横纵向一体化滚动优化决策框架,证明了优化问题的递归可行性.

2 决策系统架构

对于人类驾驶员,决策主要体现在驾驶员对车辆的操纵行为上,行为决策不易于定量表述和观测,因此,如何仿照人类驾驶员的决策定义行为是一个难点.另一方面,智能车辆的决策系统的目标是通过代替人类驾驶员做出换道和加减速的决策,进而驾驶车辆.决策系统需要满足的要求是: 在按设定驾驶车辆的同时保证车辆不与其他障碍物或路肩发生碰撞.从控制需求的角度来看,决策系统一方面需要跟踪设定的期望,另一方面,需要在道路边界的范围内,有效地避开周围环境中的障碍物,因此,是一个包含约束的,多目标的控制问题.

本文提出了一种基于混合整数规划的智能车横纵向一体化滚动优化决策方法,具体的系统结构如图1所示.该无人车系统结构包含感知、决策、规划、控制4个部分.感知部分由车上装载的惯导、激光雷达、摄像头等智能传感器及融合处理算法,输出周围障碍物信息、障碍物预测轨迹和车道信息;行为决策部分建立了简化的车辆决策模型,设计了横纵向一体化滚动优化决策方法;规划部分输入为决策出的换道动作,采用梯形加速度方法,规划出平滑的参考轨迹;控制部分包括速度跟踪控制和轨迹跟踪控制,分别跟踪参考车速和大地坐标系下的参考轨迹.

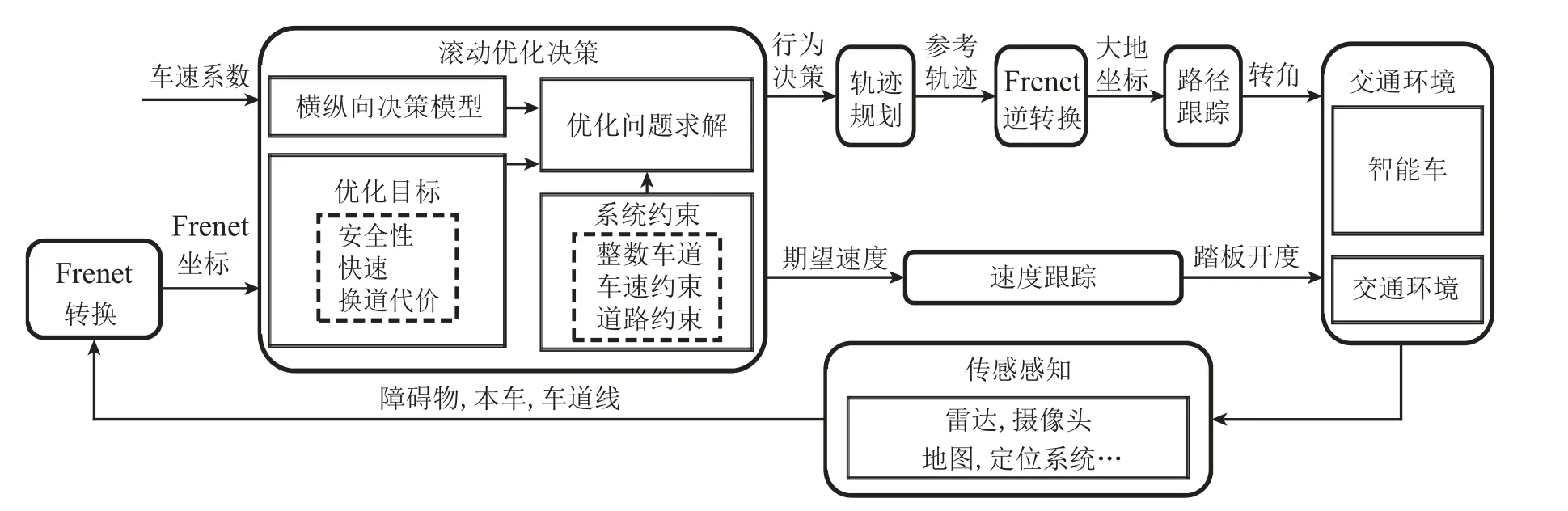
图1 基于混合整数规划的横纵向一体化滚动优化决策框图Fig.1 Block diagram of longitudinal and lateral integrated moving horizon decision making based on mixed integer programming

3 智能车横纵向决策模型

由于智能车辆的行驶离不开道路且必须遵守通行规则,所以在智能车横纵向决策建模过程中需要合理描述车与道路的关系.又因为智能车辆行驶道路的曲率、宽度、朝向、连接关系不尽相同,因此,需要研究适用于各种道路结构的决策动态过程的描述方法.

虽然道路结构多种多样,但可以利用车道描述车路关系,将所有本车可行驶的车道按从左至右依次递减的顺序编号为

其中:r为可行驶车道,rmax为最左侧车道编号,rmin为最右侧车道编号.由于车辆的道路是由车道组成的,在可行驶车道集合r中,包含所有车辆可行驶的范围.

实际中的车道由于道路限速、道路环境等因素,车道宽度不完全一致.为了便于描述车与路的相对关系,使用相邻中心线的距离d,将车与路的相对位移归一化为车道位置l0,如式(2)所示.

其中:r0为本车所在车道编号;y0为本车的侧向位移;yr0为本车所在车道中心线的侧向位移;yr0+1,yr0-1分别表示本车所在车道左右侧中心线的侧向位移;dr0+1,r0和dr0,r0-1分别表示当前车道中心线与左侧和右侧中心线的距离.

通过式(2)的侧向位置归一化,定义了车道位置,将车路关系的表示问题简化为车与车道位置的关系,描述了复杂道路环境下的道路信息和本车位移.

在得到车路关系的描述后,需要进一步建立行为决策与车辆运动的动态关系.由于驾驶规则要求车辆在一次换道过程只能跨越一条车道线,不能一次性跨越多条车道线或长时间行驶在车道线上.因此,车辆的侧向行为应包括左换道、车道保持和右换道这3个离散行为.基于决策行为的离散特性,采用整数变量定义换道动作c,如式(3)所示.

其中:c=-1表示右换道,c=0表示保持当前车道,c=1表示左换道.当左换道或者右换道决策被做出后,由底层的规划和控制层通过计算参考轨迹和控制转向盘执行该决策,并最终使车辆平滑更换到相邻的左侧或右侧车道.

为了分析智能车辆决策过程中的换道过程特性,采集了实车的换道轨迹,如图2所示.图中的蓝色实线为一次右换道过程中的车道位置状态,从实车曲线可见,当右换道决策被做出后,系统状态首先从初始车道状态l=0开始,单调递减至代表新车道的稳态值l=-1附近,并在新车道内逐渐衰减震荡至稳定.由此可见,系统的车道位置状态具有根据左右换道动作单调递增或递减的单调特性.

考虑到在同一条车道内,车辆都应按纵向位置的前后顺序依次通行,也就是一条车道在侧向上同时只能允许一辆车通行,因此车道在侧向具有独占特性.基于这一独占特性,在侧向决策过程的描述中,最重要的问题是本车当前和未来占用哪条车道,而本车处于车道中的哪一个位置的重要性则因车道的独占特性而降低.

根据换道过程的单调特性和车道的独占特性,可得需要描述的是一个状态随离散输入单调变化的、对稳态值的精度要求较高的被控对象.因此,考虑使用一阶惯性环节描述车辆的换道过程,如式(4)所示.

其中T为惯性环节的时间常数,当T越大时,系统的调节时间越长.不同的时间常数T下的模型(4)的输出如图2中的绿色点划线所示,可见T可改变系统的响应速度,进而反映车辆换道轨迹的激进与平缓.

图2 中的红色虚线为模型(4)输出的车道位置,可以看到被控对象和模型的响应终值相同且趋势一致.根据被控对象状态和模型状态的大小关系,可将系统动态过程分为换道开始阶段和稳态阶段.在换道开始阶段,模型的响应速度快于被控对象,这是因为被控对象的各级执行机构存在一定的响应延迟.而当系统接近稳态时,由于被控对象的底层控制系统的调节作用,使得系统出现了轻微的超调.

将图2中的实际车辆和模型的时域响应做差得到模型误差,图中黑线的含义为两个阶段中模型误差的最大值,开始阶段的最大误差为34.9%,稳态阶段的最大误差为36.1%.根据模型误差计算可得,模型在整个动态过程中的平均精度达到了87.8%,因此,基于一阶惯性环节的归一化换道过程描述具有一定的模型精度.

然后建立本车纵向运动模型,如式(5)所示.

其中:s为本车大地坐标系下的纵向位移,vx为本车的纵向速度.

将式(4)–(5)联立,设系统状态x=[s l]T,输出量y=[s l]T,可得决策模型如式(6)所示.

当车辆行驶在非直线的道路时,在大地坐标系下难以直接判断障碍物的沿车道方向的相对距离和所在车道,所以,需要使用坐标转换来根据车道和障碍物信息分析本车和障碍物沿车道方向的相对位置.考虑传感器所给出的本车所在车道的中心线方程为f(xo),其中xo为大地坐标系下的纵向位移.Frenet变换如式(7)所示.

其中:xo,yo为大地坐标系下待转换的坐标;x,y为转换后的Frenet坐标,x为沿车道中心线的曲线弧长,y为垂直于车道方向的侧向位移,xmin为中心线上距离xo,yo最近点的横坐标.

4 滚动优化决策

对于无人车的感知系统,经常具有的功能是预测周围障碍物的运动轨迹,即输出预测的周围障碍物运动信息.决策模块则需要基于这些预测的信息,做出车辆决策.由于模型预测控制具有预测的特性,可以有效地利用障碍物预测信息,作为控制器的约束或目标函数的一部分.因此,采用模型预测控制作为决策控制器的设计方法.

无人车决策的目标,最需要考虑的是本车的安全性,也就是本车与周围障碍物的距离.实际行驶中,不考虑周围车辆换道并撞向本车,则本车只会与本车所在车道的前后方向的障碍物发生碰撞.使车辆避免碰撞的目标函数如式(8)所示.

其中:γ为后车碰撞时间的折扣因子,0<γ <1,因为本车与前车的安全性是最需要保证的,与后车的重要性低一些;TTC为本车与前后车的碰撞时间,具体计算公式如下:

其中:Tl为低碰撞时间常数,表示两车的距离小于安全车距,认为两车会在很短的时间内发生碰撞;Th为高碰撞时间常数,表示两车的距离大于安全距离且前方车辆快于本车或后方车辆慢于本车时,认为两车可能会在很久之后发生碰撞的时间;Sk为安全距离,Sk=Thwvx(k)+dhw,其中Thw为车头时距常数,dhw为车距常数,可见本车车速越大,安全距离越大,并且当本车减速停车时,仍会保持与前后车dhw的距离;Dk(n,p)和Vk(n,p)分别为k时刻与本车当前所处的车道n相同的、相对距离最近的前后车p的相对距离和相对速度,其中p=f,r,相对距离和相对速度可由感知部分的周车轨迹预测经过大地坐标–车辆坐标系转换得出,当左侧或右侧车道不存在或不允许换道时,将该车道上前后方安全距离范围内各假定有一个障碍物,以避免车辆向该方向换道.

周车所在车道可根据周车位置和车道线的位置得到,周车纵向轨迹预测采用曲线拟合方法,即根据当前感知到的周车位置、速度、加速度,假设车辆沿车道方向的加速度在预测区间内保持恒定,本车预测的相对位移和相对速度如式(11)–(12)所示.

无人车决策的第2个目标为快速性,含义为行驶环境允许时期望的车辆行驶速度,如式(13)所示.

其中∆vx=vref-vx(k),为该路段参考车速和实际车速的偏差.正常情况下车辆应当行驶在路段的最高车速和最低车速之间,vref=(1-τ)vmin+τvmax,其中τ为参考车速系数,τ越大车速越高,行驶相同路段的时间越短,0 ≤τ≤1.如果运行中前车慢于期望速度vref,由于J1的安全性目标和J2的快速性目标的共同作用,会驱使车辆通过超车的方式,既保持安全性又保持快速性.

第3个目标为换道代价,含义为减少期望车道的变化次数,如式(14)所示.

其中∆c=c(k)-c(k-1).

系统约束包含换道动作整数约束、车速约束、道路边界约束: 换道动作的整数约束如式(15)所示.

车速约束需要考虑到当发生拥堵时,本车必要的减速停车情况,所以,车速最小值为0,如式(16)所示.

为了保证车辆安全,需要行驶在道路边界内,且道路边界与本车位置相关,如式(17)所示.

其中:lmin(s)为车道位置下界,lmax(s)为车道位置上界,是随本车位移s变化的函数,可由道路边界和车辆驾驶目标等来确定.

综上,自动驾驶车辆的决策优化问题如式(18).

其中:Y(k)为预测状态向量,U(k)为控制量向量,Syx,Syu为状态预测矩阵[21].

对于优化问题(18)的求解问题,首先,由于优化问题具有混合整数的特性,部分待优化变量是离散的,目标函数相对于整数待优化变量的梯度是不存在的.其次,因为换道动作对目标函数的影响体现在: 换道动作通过改变车辆所在的车道,进而改变了本车所在车道前后方的车辆,并最终影响式(8)中与前后车的碰撞时间,该过程具有较强的非线性特性.另外,系统的状态约束(17)中还包含系统状态间的非线性约束.最后,优化问题的约束(15)–(16)中,包含了对所有待优化变量的边界,待优化变量的范围是可以被确定的.

基于以上优化问题的4个特点,该优化问题为一个待优化变量取值范围明确的混合整数非线性规划问题.由于遗传算法在优化问题求解过程中不依赖于目标函数梯度,具有强大的最优解搜索能力且比较适用于待优化变量边界明确的优化问题[22],采用遗传算法求滚动优化决策优化问题.

优化问题要满足硬约束,就需要保证优化问题的递归可行性,即在任意约束内的初始状态,优化问题(18)都至少存在一个控制函数,使得状态满足式(6)的轨迹,并且满足状态约束和目标函数有界.下面给出递归可行性的证明.

证系统初始状态为x0=[s0l0]T,对于任意的x0,因为式(8)中的TTCf,TTCr均大于0,所以J1有界.又因为J2,J3显然也有界,所以加权求和的目标函数J对任意x0和U(k)都有界.

因为控制函数约束(15)–(16)的上界始终大于等于下界,所以,存在满足该约束的控制函数.因此,只需证明控制函数约束内,至少存在一个控制函数,使系统满足状态约束(17).证毕.

假设车道左右边界连续,选取任意一条在道路边界内的轨迹为参考轨迹,都有

其中lmax(s0)和lmin(s0)为s0处的车道位置边界.

控制量u的作用下,系统(6)响应如式(20)所示.

可见,系统响应与初始状态和换道动作有关.

将车道位置边界描述为初始位置的边界和变化量,如式(21)所示:

其中∆lmax(s)和∆lmin(s)为车道位置边界相对于s0的变化量.

系统满足约束(17)的条件为

将式(20)和式(21)代入式(22)可得

又由式(21),得∆lmax(s),∆lmin(s)连续,且∆lmax(s0)=0,∆lmin(s0)=0.可选取控制动作c=0和vx<ε,使得系统状态s满足

此时系统轨迹一定满足约束(17),式(25)表明: 当道路边界变化时,只需降低车速,以使车辆有充足的时间调整侧向位置,即可保证车辆行驶在道路边界内.

由于优化问题是递归可行的,可以在每个采样时刻用最新的测量值刷新优化问题并重复求解优化问题(18),然后将求解出的vx和c的第1个元素分别作用于车辆的纵向速度跟踪控制器和换道轨迹规划模块中,即可实现车辆的决策.

5 结果讨论

为了验证基于混合整数规划的智能车横纵向一体化滚动优化决策方法的性能,基于高精度车辆仿真软件veDYNA-Simulink联合仿真及红旗E-HS3智能车实车试验对方法有效性进行了验证.其中,纵向速度跟踪部分采用PID控制器跟踪参考速度vref,侧向轨迹规划部分采用梯形加速度方法[10],路径跟踪采用基于模型预测控制(model predictive control,MPC)的多点预瞄方法跟踪参考轨迹.由于路径规划模块不具有避障功能,且速度跟踪和轨迹跟踪模块跟踪的参考值均为滚动优化决策方法的输出,所以,结果中的换道、加减速的行为均由决策部分产生,可以验证决策方法的效果.决策算法参数如表1所示.

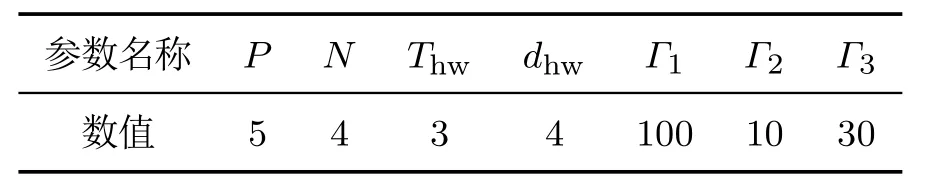
表1 决策算法参数Table 1 Decision algorithm parameters

选取最小车距Dmin作为评价指标,以判断车辆是否发生了碰撞,具体定义如下: 定义本车和周车纵向中线的处两点为点Sf,Sr,任意时刻本车Si(t)点与任意周车上的Sik(t)点的最小距离减去2倍的Si点到车边缘的半径即为最小车距(i=f,r),如式(26)所示.

如果最小车距Dmin≥0,则本车没有发生碰撞.

5.1 veDYNA-Simulink联合仿真

分别进行了超车、避障、跟车、停车和弯道5 种情况下的仿真验证,仿真中设置路段的最低速度为90 km/h,最高速度为120 km/h,参考车速系数τ=0.5,本车和障碍车车长l=4.965 m,车宽w=1.795 m.其中: 图3–7 中的(a)图为本车和周车在不同时刻的位置,红色图例表示的为最小车距最小时刻本车与周车的位置,本车为蓝色空心矩形,障碍物为红色实心矩形;图3–7中的(b)图为决策出的参考速度和实际车速.

图3 超车仿真结果Fig.3 Simulation at overtaking

图3为超车情况下的仿真,用来模拟的是前方有慢车时的工况.该工况中平行于本车的左侧车道和本车前方100 m 处的右、中车道上,均有行驶速度为90 km/h的障碍车.对于前方存在慢车的这种工况,车辆的可选决策是减速或换道超车,由于减速会影响本车的运行效率,所以,比较合适的是选择换道超车.

从图3(a)中可以看出,本车在距前车距离较远时开始换道超车,并在左侧车道超过前车,换道轨迹较为平滑.从图3(b)中可以看出,本车在超车时出现了轻微的减速,短时间后即加速至期望车速.从整个仿真结果来看,决策算法正确的做出了换道超车的决策.

图4为避障情况下的仿真,用来模拟的是道路中出现静止障碍物的情况,例如,出现修路或封闭车道等情况.平行于本车的右侧车道和本车前方100 m处的左、中车道上均有一个静止障碍物.该工况下,为保证通行效率,本车应当换到右车道上继续行驶,而不应该在障碍物前停车.

图4 避障仿真结果Fig.4 Simulation at avoiding obstacles

从图4(a)中可以看出,本车正确做出了左换道的决策.从图4(b)中可以看出,由于静止的障碍物对本车的危险比低速运动的障碍物的碰撞风险更大,所以,避障工况下期望车速下降的更多,以保证车辆安全.由于障碍物的出现,本车首先减速,然后,加速超过障碍物.

图5为跟车情况下的仿真,用来模拟的是车辆密集、整体通行速度较低的场景.本车前方100 m处的左、中、右车道分别有行驶速度为90 km/h的障碍车.该工况下,本车应当降低车速并与前车保持安全距离.

图5 跟车仿真结果Fig.5 Simulation at following

从图5(a)中可以看出,本车沿着本车道行驶,逐渐缩短与前车的车距,最终与前车保持了安全的跟车车距.从图5(b)中可以看出,本车逐渐降低期望车速,但在稳定后出现了期望车速的波动,原因在于TTCf被定义为分段函数,此时,本车与前车的车距在安全车距附近,且最优的车速也与前车车速相近,所以TTCf出现了频繁的切换.从整体来看,虽然车速在一定范围内出现了周期性的抖动,但车辆未出现碰撞的情况.

图6为停车情况下的仿真,用来模拟高速上出现事故等需要本车停车的场景.本车前方100 m 处的左、中、右车道分别有静止的障碍物.该工况下,本车应当减速停车以保证安全性.

图6 停车仿真结果Fig.6 Simulation at stopping

从图6(a)中可以看出,本车在中间车道逐渐接近前方的障碍物,并最终停在障碍物后方.从图6(b)中可以看出,本车的期望车速逐渐降低并减小至0.整体来看,本车车速随车距的减小逐渐降低,最终停在了障碍物前,保证了车辆的安全性.

图7为弯道下的仿真,用来验证复杂工况下的算法效果.本车前方200 m处的左、中车道,前方400 m处的右车道分别有静止的障碍物.该工况下,本车应当在跟上弯道的前提下实现换道超车.

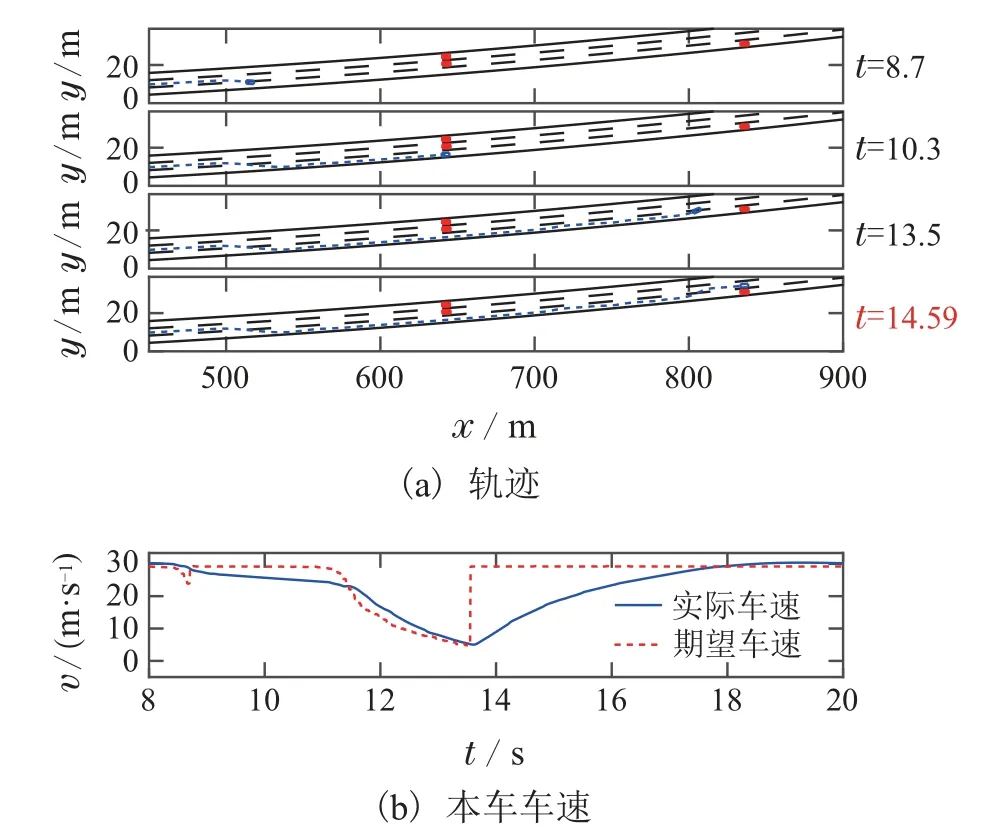
图7 弯道仿真结果Fig.7 Simulation at curve

从图7(a)中可以看出,弯道情况下本车在车道区域内完成了2次超车,并且第1次超车时与前车保持的车距大,第2次超车时,由于后方有障碍物,所以超车时与前车的距离相较于第1次更小,在本车的后方留出了安全空间.从图7(b)中可以看出,在第1次换道超车的过程中,没有明显的减速就进行了超车,保证了本车的行驶效率;而在第2次换道超车时,由于前后方障碍物之间的距离有限,本车首先降低车速缩短与前方障碍物的距离,以保证本车与前方障碍物的安全性,然后进行了换道超车.综合图7可以得出,提出的滚动优化决策可以实现如弯道下的换道避障且旁车道有障碍物的复杂情况下的智能车决策.

5种仿真工况下的安全距离如表2所示.

表2 安全性能指标Table 2 Safety performance index

从表2中可以看出,5种工况下的最小车距均大于0,车辆与其他障碍物没有发生碰撞.其中超车、避障和弯道工况的最小车距比较小,原因在于本车均超越了障碍物,最小距离为本车和障碍物的侧向距离.而跟车和停车工况下没有超越障碍物,最小距离为纵向距离,且跟车情况下的最小车距大于停车工况的最小车距,是因为跟车时本车车速较大,本车保持了相比停车时更大的车距来保证安全.

5.2 实车试验

为了进一步验证模型的精度和算法的有效性,在红旗E-HS3智能车平台上对算法进行了实车试验.智能车平台结构如图8所示,其中加装了测量本车运动状态的OXTS RT2000惯性导航系统,进行实时滚动优化决策的dSPACE MicroAutoBox III 车载计算平台,以及通过CAN总线发送车身状态和执行控制动作的车载ECU,障碍物及车道线由虚拟的障碍桩模拟.

图8 红旗E-HS3智能车平台Fig.8 Hongqi E-HS3 intelligent vehicle platform

出于安全考虑,试验在封闭道路内进行,且设定参考车速为10 km/h,结果如图9所示.图9(a)中红色圆形为障碍桩,蓝色曲线为本车轨迹.可以看出,本车行驶在了道路区域内,且先后正确地做出了右换道和停车的决策.图9(b)中蓝色实线为车辆的实际车速,红色虚线为决策出的期望速度,试验过程中,智能车从静止状态自主换挡启动并跟踪期望速度.在右换道阶段,智能车在做出换道决策的同时开始加速超越障碍物,当行驶到不可通行的路段时,逐渐降低车速至完全静止.图9(c)–(d)分别为侧向速度和侧向加速度,可以看出,在实车传感信号中存在较大的测量漂移和噪声,在换道过程中,车辆的侧向速度向右并随着换道过程的结束恢复至0,侧向加速度的方向为先向右后向左.图9(e)中为车辆方向盘转角和由底层路径跟踪控制器得出的期望方向盘转角,可以看出,车辆的期望转向动作是平缓的,且车辆执行机构存在一定的响应延迟.

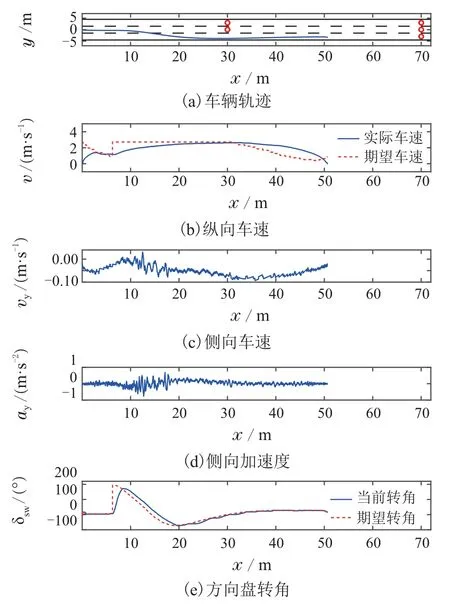
图9 试验结果Fig.9 Experiment result

从实车试验的结果来看,尽管智能车辆系统十分复杂,本文提出的横纵向决策模型仍然可以描述实际智能车决策过程中的主要特性.并且,本文提出的基于混合整数规划的横纵向一体化滚动优化决策方法可以有效实现车辆的横纵向决策.

6 结论

本文提出了一种基于混合整数规划的智能车横纵向一体化滚动优化决策方法,通过将侧向的期望车道描述为整数控制量建立了决策模型以描述车辆换道的运动特性,设计了横纵向一体化滚动优化决策算法并通过遗传算法求解出包含纵向车速、期望车道的横纵向决策.本文通过联合仿真和实车试验对算法进行了验证,结果表明滚动优化决策方法提升了决策算法的可解释性和预测性,保证了智能车决策的有效性和车辆的安全性.笔者在后续的研究中,将考虑结合决策优化问题的特性和改进的分支定界法或割平面法等混合整数规划问题求解理论,研究能够保证最优性和实时性的决策优化问题求解方法,并考虑加入换道时间作为决策的控制量,以提高换道决策的灵活性.