融合元学习和PPO算法的四足机器人运动技能学习方法
朱晓庆,刘鑫源,阮晓钢,张思远,李春阳,李 鹏
(北京工业大学信息学部,北京 100020;计算智能与智能系统北京市重点实验室,北京 100020)
1 引言
近些年,移动机器人由于可在多种场景下完成任务受到广泛关注,移动机器人被分类为:轮式机器人、履带式机器人和足式机器人[1];由于结构问题,传统轮式机器人和履带式机器人可应用的场景范围较小,在非平坦地形上,存在越障能力差以及由于地形多变而造成重心不稳等问题[2].相反,足式机器人由于其仿生的腿部结构而拥有更高的灵活性和适应性,可以像动物一样在各种地形完成行走任务[3–4].根据足数量的不同可以将足式机器人进行分类,相较于双足机器人和六足机器人,四足机器人在结构上具备更稳定和更易控制的优点.正因此四足机器人在医疗、物资运输、环境勘探和资源采集等场景中具备很大的应用前景.通过人为指定运动速度的方式,使机器人具备像动物一样的行走姿态[5],这种方法需要人为设置控制器.然而,这种控制器的设计流程更为繁琐,特别是针对机器人的系统和腿部的控制器,不仅对设计者的专业知识水平有较高的要求,而且,在实际应用过程中,控制器的具体参数也需要反复调整和试验[6–7].
强化学习[8]具备让智能体自己学习的能力,近年来该技术在各应用领域蓬勃发展[9–11].在机器人设计、操作、导航和控制等方面,也以此为基础不断拓展[12–13].为了解决传统的基于人工设计的控制器存在的问题,越来越多的研究使用强化学习来代替原有设计方式[14],Kohl和Stone[15]在底层控制器设计完善的基础上,通过强化学习调整控制器参数,训练出了四足机器人Aibo 的行走控制策略,代替原有的手动设置参数的过程,并且由强化学习训练的步态行走速度快于当时手动调参可达到的最快步态;Peng等人[6]先对动物的动作进行捕捉,得到四足机器人目标动作,之后利用强化学习来让四足机器人完成目标动作,实现了让机器人通过模仿动物来学习运动技能;ETH 团队[16]引用策略调整轨迹生成器(policies modulating trajectory generators,PMTG)架构,即设计一个轨迹生成器作为先验,再通过强化学习对前面轨迹生成器进行调整,其中应用了课程学习[17],教师策略中通过编码器将视觉信息和本体感知信息融合编码成隐变量,再让学生策略通过机器人的历史状态来提取隐变量得到机器人的控制策略,并通过在机器人建模时使用随机化处理和训练神经网络电机模型实现了将强化学习算法实际部署在物理机器人上,完成了多种地形上的鲁棒性行走[18–20].上述研究或通过良好的运动先验知识或通过精心设置的奖励函数实现了机器人步态学习和在物理机器人上的部署,然而如何在少量运动先验前提下,通过简单奖励函数快速有效地学会四足机器人步态仍是一个正在面临的挑战.
本文在Shi等人的研究[21]基础上,提出一种基于生物启发的元近端策略优化(meta proximal policy optimization,MPPO)算法,在有运动先验知识的情况下,仅通过简单奖励函数来快速学习机器人行走技能,和现有强化学习算法柔性行动者评价器(soft actor-critic,SAC)和近端策略优化(proximal policy optimization,PPO)的对比试验结果来看,本文的算法具备一定程度的有效性.
2 算法设计
2.1 近端策略优化算法
对于机器人系统,策略梯度(policy gradient)算法针对连续动作空间的任务,可取得显著成效,传统策略梯度算法的基本思想是通过最大化状态价值(value)函数Vπ(s)来更新策略(policy)函数,即直接去优化策略网络,更新策略函数的损失函数被定义为
其中f(s,a)为在状态s下采取动作a的评估,策略的梯度表示为
最后通过式(3)更新参数θ
其中φt有多种计算方法,通常被表示为优势函数(advantage function),如式(4)所示,作为一个衡量当前动作好坏的标准,如结果为正,证明当前动作a在此策略下要更好,并且之后提高此动作的概率以优化策略,即
将式(4)代入式(2)得到
然而,传统的策略梯度算法在计算式(4)–(5)时会因偏差和方差的问题导致无法准确估计优势函数.以下考虑两种极端情况,以整条轨迹来估计优势函数时虽然不会有偏差,但是会有高方差的问题,即过拟合;假如以单步更新,虽然不会有方差,但会有很大的偏差,即欠拟合.因此,需要在这两种极端情况中间找到一个平衡,但是优势函数估计的偏差是无法避免的,导致算法性能对更新步长十分敏感,假如一次更新步长过大,将可能会导致下次采样完全偏离,也就导致策略偏离到新的位置,从而形成恶性循环.为了解决这个问题,PPO算法[22]在信任域策略优化(trust region policy optimization,TRPO)[23]的基础上被提出.PPO算法在策略梯度这个同策略(on-policy)算法的基础上引入了重要性采样(importance sampling),将其变成了一个近–异策略(near off-policy)的算法.
上式为重要性采样过程,将式(6)代入式(5)得到
只计算t时刻的梯度公式就变为了
于是损失函数由式(1)变成了
作为一个策略梯度算法的优化算法,PPO算法核心思想是通过对式(9)引入截断(CLIP)限制更新幅度,让每次策略更新后落在一个信任域(trust region)里,以此解决了更新步长的问题,PPO算法的损失函数如式(10)所示:
其中:ϵ是超参数,用来限制更新的大小;是优势函数在t时刻的估计值.最终训练时的损失函数为
与TRPO算法相比,PPO的超参数较少,在计算上更易实施,且效果更好,因而受到广泛的关注和应用.
2.2 MPPO
PPO具有在大部分实验环境中有很好效果且具有较少超参数的优势,但是在多维输入输出场景下,如本文涉及的四足机器人步态学习任务实验环境中的呈现效果一般,且容易收敛到局部最优,表现为步态节律信号杂乱、重心震荡严重.为此,本文在融合元学习的基础上提出了MPPO算法.
不可知模型元学习(Model-agnostic meta-learning,MAML)[24–25]由元学习(meta learning)引出,元学习优势体现在可快速适应新任务且减轻过拟合现象.从特征学习角度看,元学习训练的模型参数通过少量梯度更新能在新任务上产生良好结果,这样的过程可被视为构建广泛适用于许多任务的模型本质表示.从系统角度看,元学习是最大化了新任务损失函数对参数的敏感性: 灵敏度较高时,参数微小局部变化可导致任务损失的大幅改善.本文提出的MPPO算法,融合元学习和强化学习思想,即不是找到当前观测下的最佳参数,而是希望找到可以广泛适应在不同观测上采样到的数据上的参数,让四足机器人遵循奖励函数学习到运动技能的本质,获得更高奖励值并达到更优步态.
其算法伪代码和框图如表1和图1所示.
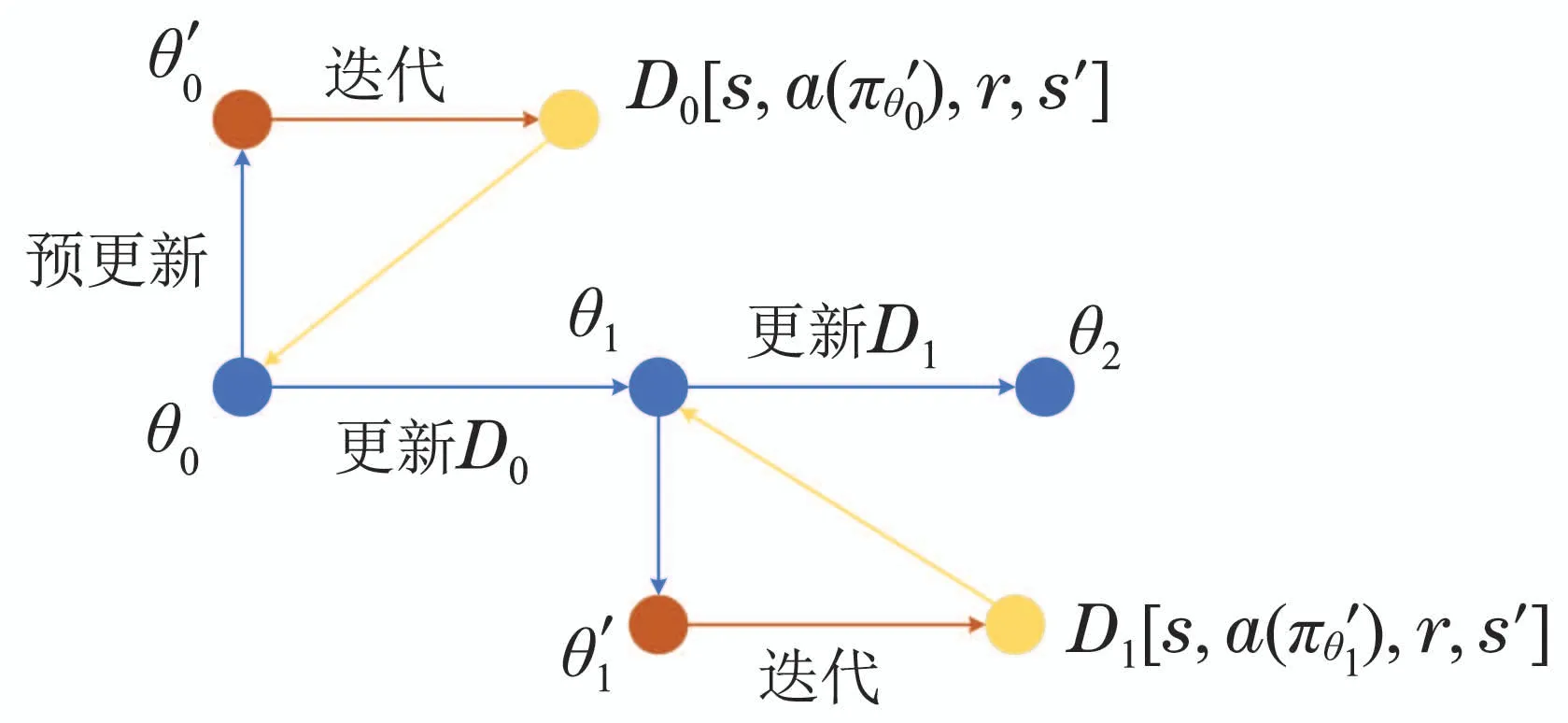
图1 算法框图Fig.1 Algorithmic flowchart

表1 算法1: MPPO算法伪代码Table 1 Pseudocode
首先,使用全局策略和环境交互,并通过PPO算法流程更新参数得到预更新的参数.由于PPO策略的输出动作是一个高斯分布的采样结果,其训练方向会很多样.通过和环境的交互收集到的D0[s,a(),r,s′]作为数据用于更新策略,这步可以看作一个有预见性和兼顾性的预更新,对应了元学习中通过单个任务的训练误差更新一个中间策略,通过中间策略把当前任务上的测试误差作为元学习训练误差的更新方法,即不追求当前状态下的最优方向,转为追求下一状态下的优势方向,以此更新全局策略.在本文中,PPO算法的演员(actor)和评判家(critic)网络都采用了长短期记忆网络(long short-term memory,LSTM)[26]网络,相比多层感知器(multilayer perceptron,MLP)网络,其对像机器人系统这样序列型的输入有更好效果.
3 实验
3.1 实验对象
本文使用pybullet物理引擎[27]在gym环境中进行模拟实验,机器人为Laikago,它是一个12自由度的四足机器人,每条腿有3个自由度,分别为髋关节、摆动关节和膝关节,控制频率为38 Hz,其身体参数即各关节活动范围如表2所示.
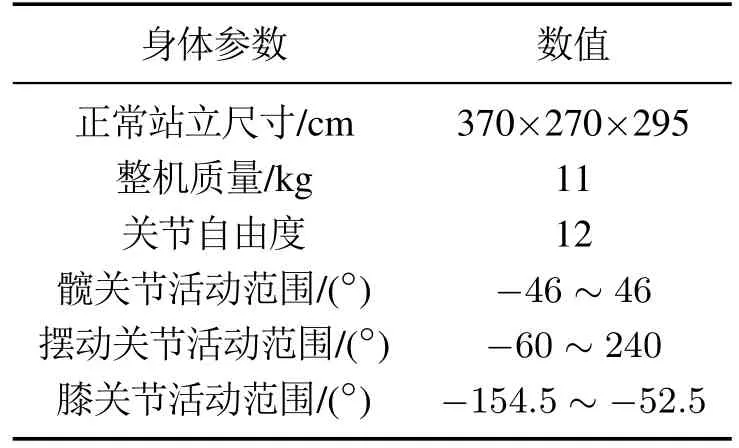
表2 四足机器人身体参数Table 2 Body parameters of quadruped robot
3.2 实验设计
为了验证本文MPPO算法有效性,将此算法和传统SAC[28]和PPO算法进行对比实验,实验设置如下.
3.2.1 奖励函数
在强化学习问题中,奖励函数可以被视为智能体的目标,在智能体与环境交互的每一个时刻中,当遇到状态时,智能体会根据策略选择一个动作(action),同时由设定的奖励函数给出一个奖励值(reward),而智能体的目标就是学习到一个策略来最大化这个奖励,因此这个奖励函数的设置应与想达到的训练目标相匹配,通过奖励函数来教会智能体一个期望的技能或者说引导智能体的策略向期望的目标上发展.
在本文使用的策略梯度算法中,首先通过设计奖励函数引导价值函数向其靠拢,再通过价值函数来引导策略进行学习,以此让机器人学习到期望的行走技能.为了让机器人学会平稳快速节能的行走,奖励函数被设计为
其中c1,c2和c3为各部分奖励函数之间的系数.
其中:Xt代表机器人所处位置,t为根据控制频率计算的时间,这部分的奖励函数是为了鼓励机器人朝着期望的方向前进并且速度越快越好.
其中Et代表能耗,这部分的奖励函数是通过负的系数来促使机器人兼顾能耗问题.
其中: roll和pitch为机器人惯性运动单元(Inertial motion unit,IMU)测得的俯仰角和横滚角,这部分的奖励通过一个双曲正切函数来引导机器人以更平稳的姿态行走.
3个系数的大小影响了3个部分在奖励函数中的重要程度,通过这3部分奖励之间相互制约,机器人学会了一种兼顾速度稳定和低能耗的行走技能.
3.2.2 训练流程
本文实验训练流程图如图2,为了加速训练过程,采用类似文献[14]的实验框架,受残差控制[29]启发,机器人输出由acpg(t)和amppo(t)两部分构成,acpg(t)作为运动先验知识输出一个周期性的节律信号[30];amppo(t)作为残差信号,其中amppo(t)策略的输入即状态是49维的由3部分构成: 1)12维的运动先验中枢模式发生器(Central pattern generators,CPG)参数;2)34维的机器人状态信息,其中24维是机器人的电机信息,包含4 条腿的髋关节和2个膝关节的角度和速度,6维机器人质心姿态信息包含位姿(俯仰,横滚,偏航)与加速度(x,y,z3个方向)各3 项,4维的足端接触检测信息(检测每条腿是否触地);3)3 维机器人的位置信息(包括x,y,z3方向的位移).输出即动作是12维的期望位置,即每条腿髋关节和2个膝关节电机的期望位置,叠加成为机器人的动作输出.动作合成后,由比例微分控制(Proportion Differential,PD)控制器来跟踪实现对机器人腿部的控制.为了维持训练过程稳定性,两部分的动作网络采取分时训练[21]方法,即训练过程中先固定acpg(t)网络的参数,并根据MPPO的算法流程更新amppo(t)的参数,当交互够N步后,固定amppo(t)的网络参数,通过进化算法对acpg(t)进行更新,当一个网络参数进行训练的时候另一个网络就维持参数停止训练.
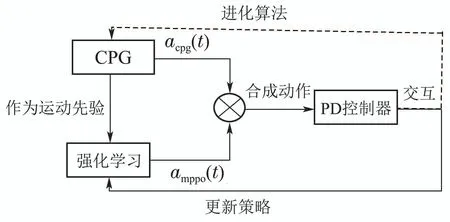
图2 训练流程图Fig.2 Training flowchart
4 实验结果
本实验使用笔记本电脑,训练过程中每2048步作为一个回合(episode),并在每个回合结束时进行一次评估.按照第3节设计的实验流程进行训练1训练过程视频: https://www.bilibili.com/video/BV1Q24y117EQ/?vd_source=4b5a3b89f1ef3731413895e73cb00b7e.,训练过程中四足机器人的行走步态和身体数据如图3–4所示.
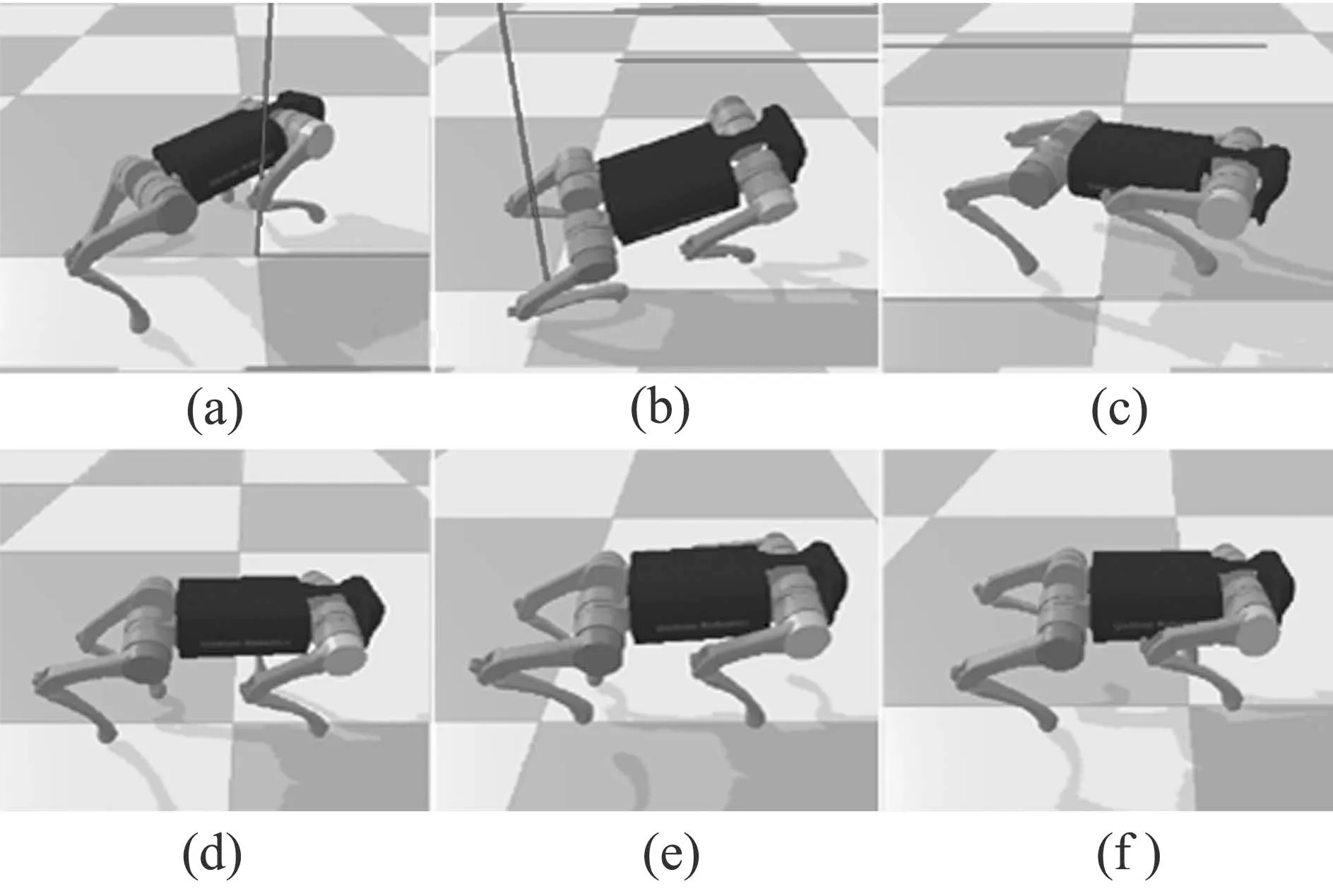
图3 四足机器人行走步态学习过程截图,其中(a)–(c)为训练初期,(d)–(f)为训练末期Fig.3 Screenshot of quadruped robot walking gait learning process.At the beginning of training,it appears as(a)–(c),and at the end of training,it appears as(d)–(f)
从图3(a)–(c)和图4可看出,在训练初期,四足机器人步态非常不稳定,身体上下晃动幅度在0.21到0.26之间,呈现较大且不规律的晃动,无法以正常姿态前进.随着训练进行300个回合时,机器人步态及身体数据如图3(d)–(f)和图4所示.可看出,在训练完成时,机器人的步态呈现出对角接触步态,行走过程中,身体的上下晃动幅度较小,在0.24到0.265之间,高于刚开始训练质心高度并呈现稳定的节律行走步态.该训练结果是由奖励函数中的引导而来.对比上图训练开始时和训练结束时机器人行走质心高度的变化可看出,训练完成后机器人行走时更稳定且质心高度更高.
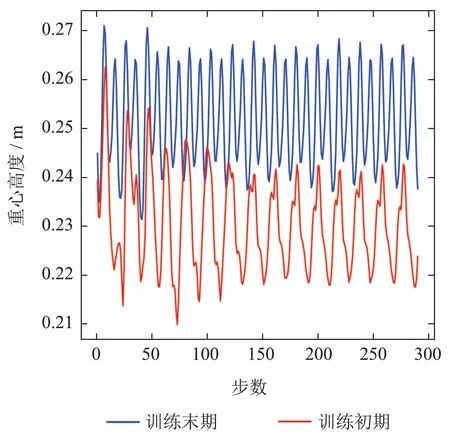
图4 训练前后机器人行走质心高度变化曲线Fig.4 Height variation curve of robot walking centroid before and after training
图5是训练过程中的奖励值,从中可以看出,本文提出的MPPO算法在四足机器人步态学习的任务中,奖励值可以从零开始迅速上升,大约到75个回合时,收敛于4000左右,75回合之间的过程是四足机器人从初始状态开始学习到可以初步完成行走任务的过程,训练回合超过75回合之后,奖励值缓慢上升至4500左右,并且策略趋于收敛,代表完成行走步态的学习.
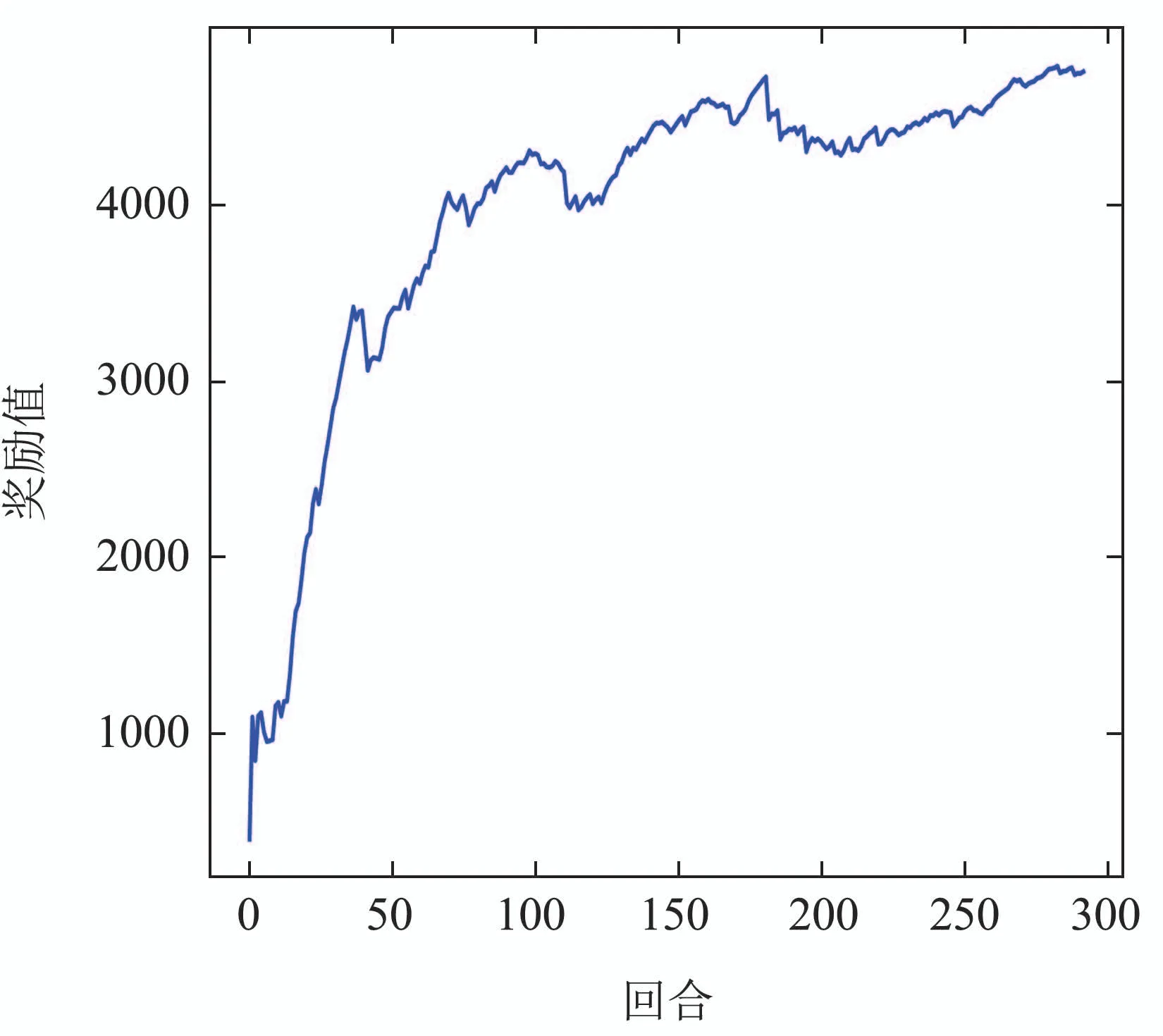
图5 训练过程奖励值Fig.5 Rewards during training
图6和图7分别是机器人行走距离和行走偏移变化曲线,横坐标为回合数量,纵坐标分别为训练过程中机器人行走距离(每一次评估最多进行500步)和行走偏移量,虚线为期望前进方向即0偏移.图6中看出,本文提出的MPPO算法在行走距离上从零开始迅速上升,在20个回合左右行走距离达到12 左右,并在后续逐渐波动,最终在250个回合左右收敛至11.偏移量在100到150回合中逐渐变大,在150到200步逐渐变小,最终在300步时收敛到–0.1左右.这种笔直前进步态是由奖励函数中部分引导而来的.

图6 机器人行走距离变化曲线Fig.6 Variation curve of robot walking distance

图7 机器人行走偏移变化曲线Fig.7 Variation curve of robot walking deviation
5 讨论与总结
5.1 讨论
为了验证本文算法的优势,本文将传统的PPO算法和传统的SAC算法与MPPO算法进行了对比试验.在四足机器人步态的全部训练过程中,每2048步设置为一个回合,并且在每一个回合进行一次数据评估,实验结果如图8所示.
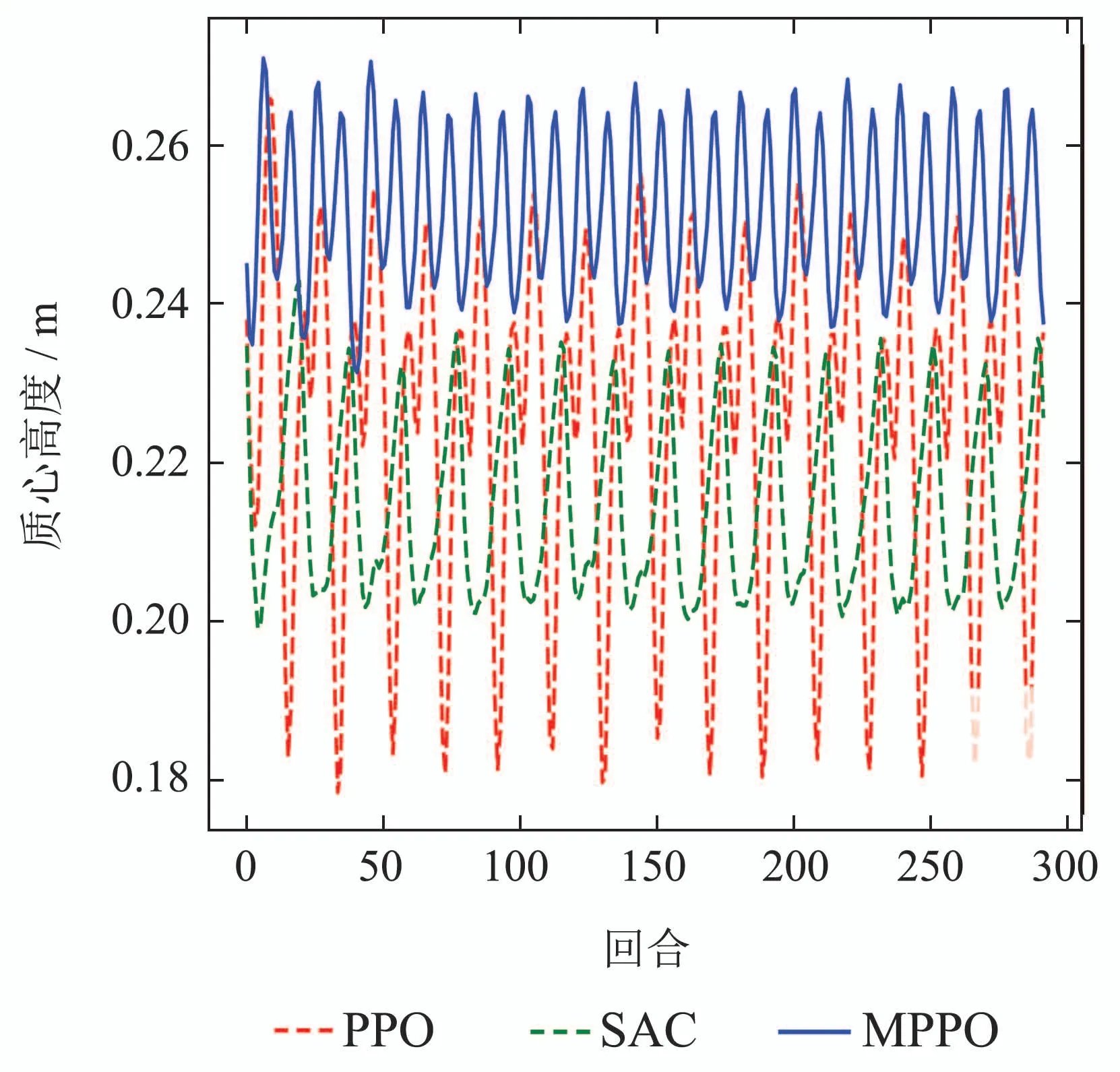
图8 机器人质心高度变化曲线Fig.8 Height variation curve of robot centroid
训练完成后分别对3种算法训练出的四足机器人步态进行行走测试2,图8为机器人行走测试中质心高度的变化,可看到本文提出的MPPO算法训练结果相比较于传统PPO算法和SAC算法,行走步态质心起伏幅度更小,说明本文提出的MPPO算法训练出的四足机器人步态有更好的稳定性;并且MPPO算法训练的行走步态的质心高度整体高于传统的SAC和PPO算法,说明其行走步态使机器人在行走过程中拥有腿伸展程度更高,因此可以迈出更大的步伐.
图9为训练过程中机器人行走的距离曲线,横坐标为回合数量,纵坐标为评估一次机器人行走的距离(每一次评估最多进行500步).从图中可看出,本文提出的MPPO算法在行走距离上从零开始迅速上升,在20个回合左右行走距离达到12左右,并在后续逐渐波动,最终在250个回合左右收敛至11.相较于传统SAC算法在20–50个回合行走距离从6上升至10,最终收敛至9.和传统PPO算法在前100个回合有起伏最终收敛于6左右的实验结果.在相同上限步数的情况下,行走更远的距离就相当于拥有更大的步长和更快的速度,此实验结论和对比机器人行走时质心高度变化曲线得到结论相同,即本文提出的MPPO算法训练出的行走步态有更大的行走步长和更好的稳定性.

图9 训练过程机器人行走距离曲线Fig.9 Walking distance curve of robot during training
从图10中可看出,本文提出的MPPO算法在四足机器人步态学习的任务中,奖励上升幅度大,且最终收敛时的奖励值最高.

图10 训练过程奖励值Fig.10 Rewards during training
而传统的SAC算法在有先验知识的基础上奖励值先降低后缓慢升高,大约到100回合的时候,奖励值收敛到3000左右,训练效果略低于本文提出算法;传统PPO 算法在训练过程中奖励值略微升高后就急剧下降,收敛至2000左右陷入局部最优,训练效果远小于传统SAC算法和本文提出的MPPO算法,由上可知,本文所提出的算法在四足机器人步态学习的任务中效果优于传统的强化学习算法.
5.2 总结
为阐明复现高等生物的运动技能学习机理,本文以四足机器人为研究对象,基于强化学习框架探究四足机器人技能学习算法,鉴于元学习具有刻画学习过程高维抽象表征优势,本文将元学习引入了PPO算法,提出了一种MPPO算法.以四足机器人行走步态作为任务进行学习训练,仿真实验结果验证了该算法可行性.本文提出的算法,仅需简单设计的奖励函数即可使得四足机器人学会走起来,并且相比较于SAC算法和PPO算法,本文的MPPO 算法不仅在训练速度上有一定的优势,并且训练出的步态也呈现更佳效果,如其质心姿态更加平稳,震荡小.对比实验结果表明本文提出的MPPO算法具有兼顾性和预见性优势,可以解决四足机器人步态学习过程中出现的局部最优问题,学习到更优步态.后续将继续在MPPO算法中引入动态奖励函数,以获得更快的收敛速度以及更稳健的更新方向,并且在多地形任务上进行实验.在完成仿真实验后,将进行实物实验.

