随机Lur’e时滞网络的指数同步与脉冲控制

孔纬升 汤 泽 王 艳 纪志成

(1.江南大学物联网工程学院,江苏 无锡 214122;2.江南大学物联网应用技术教育部工程研究中心,江苏 无锡 214122)

1 引言

近年来,在网络科学以及控制理论等诸多学科中,复杂系统与动态网络的同步成为热点问题,引起了诸多学者的广泛关注[1].复杂网络是具有小世界、无标度和集群等特性的网络,它由节点和边组成,其中节点用于表示现实系统中的不同个体,而边用于表示节点之间的个体关系.实际上,同步是自然界普遍存在的现象,如钟摆的同步、剧场内掌声的同步、萤火虫的同步等,同步意味着每个节点的状态变量相互收敛,这可以通过相互交换节点信息来实现.因此,同步在故障检测、信号处理、网络通信具有重要的潜在应用价值.到目前为止,已经逐渐研究了许多同步模式,例如广义同步[2]、聚类同步[3]和相位同步[4]等.

Lur’e 系统是由前苏联学者Lur’e 在世提出的[5].Lur’e系统是一个典型非线性系统,可以看作是一个由一个非线性系统和一个满足扇区有界约束条件的非线性反馈组成的闭环系统.Lur’e系统包括Lorenz系统、Goodwin模型、蔡氏电路等,广泛用于航空航天和液压伺服控制等诸多工程和技术领域.

由于网络控制系统中放大器的有限交换速率和信号传输时间[6],导致了时滞现象在网络中普遍存在.事实上,具有线性耦合配置和时滞的Lur’e网络易于物理实现,因此具有很大的潜在应用价值,特别是在基于同步的航空航天领域.时滞对系统的动态行为有很大的影响,在一定程度上会改变系统趋于同步的速率.时滞一般具有时变等特性,而时变时滞的部分特性是已知的,比如其上界,同时时变时滞可以是非平滑的.在网络建模中,若对时滞的描述不够准确,会导致设计缺陷和分析结果不准确.例如,文献[7]研究了具有参数不确定性的时滞Lur’e 系统的同步.此外,Li 和Chen[8]用线性矩阵不等式讨论时滞动态网络的同步.

实际上,只有少数复杂动态网络可以通过改变系统本身的特性和网络的耦合强度来实现同步,而大多数复杂网络需要通过外部控制输入来实现同步.因此,设计高效控制器已成为复杂网络同步中的一项关键问题.随着研究的不断深入,出现了不同的控制策略,如牵制控制[9]、自适应控制[10]、脉冲控制[11]、间歇控制[12]和事件触发控制[13].其中,脉冲控制作为一类典型的离散控制方法,只有在脉冲发生的时刻才会被激活.在许多脉冲控制或脉冲扰动问题中,网络状态的切换现象、频率变化或其他突发噪声的瞬态扰动和在某些瞬间发生突变是不可避免的,因此需要考虑不同的脉冲效应.在系统相互交换信息的过程中,脉冲效应既可以起到积极作用,也可以起到消极作用.这意味着脉冲效应不仅能加快网络同步,而且可能阻碍甚至破坏整个系统的同步.例如,文献[14]利用脉冲控制和稳定性定理研究了不确定动态网络的鲁棒脉冲同步.此外,通过建立脉冲时滞微分不等式,文献[15]考虑了具有脉冲效应的神经网络.

基于上述考虑,本文将研究脉冲控制下时滞耦合Lur’e网络的全局指数同步问题,为了模拟现实世界,在同步分析中将考虑随机现象.由于现实网络受通信通道带宽等条件限制,故节点之间的信息交换很难以线性、对称的形式进行.因此,本文通过一致性地考虑正负脉冲效应,提出了随机Lur’e时滞网络实现全局同步的充分条件,且给出网络的收敛速度.最后,通过不同脉冲效应的数值仿真验证了所提出的控制策略的有效性.本文的主要贡献可以概括为以下3点: 1)与现有大多数研究相比,如文献[16–17],本文一致性地讨论了正负脉冲效应对网络群聚行为的影响,以确保实现随机Lur’e动态网络全局指数的同步;2)在不设置参照系统的情况下,通过引入Perron-Frobenius定理并构造一个新颖的Lyapunov函数,仍可以在耦合网络内实现同步,即巧妙地应用了无参照系统策略,这明显区别于现有的相关工作,如文献[18–19];3)结合平均脉冲间隔概念、Lyapunov稳定性定理、比较原理和参数变分原理,给出了随机Lur’e时滞网络实现全局指数同步的充分条件.值得注意的是,在不同的脉冲效应下,Lur’e网络的收敛速度不是一致的,且收敛速度直接受时变时滞上限的影响,而在文献[20]中,不同的脉冲效应则导致一致的收敛速度.

2 准备工作

考虑随机Lur’e系统耦合而成的时滞网络模型

为了给出同步的判定条件,下面本文首先给出一些相关的定义、假设和引理.

定义1[20]假设在时间段(t,T)内脉冲信号序列为ζ={t1,t2,···},Nζ(T,t)代表了在脉冲序列的脉冲次数.如果存在两个正数N0和Na满足以下不等式:+N0,0 ≤t≤T,那么脉冲信号序列的平均脉冲间隔小于Na.

定义2[21]考虑复杂网络(1).如果对于任意初始条件ϕi(t)∈C([-τ1,0],Rn),存在标量λ>0,T0>0和ρ>0,使得当t>T0时有

则称复杂网络(1)实现了全局指数同步.此外,λ被称作收敛速度.

假设1非线性函数f1(·)和f2(·)满足利普希茨条件,即意味着对于任意向量x,y ∈Rn,都有

其中l1和l2是正常数.

假设2假设噪声强度函数矩阵:R+×Rn →Rn×m根据矩阵上的迹内积引起的范数是一致利普希茨连续的

其中M是一个具有兼容维度的已知常数矩阵.

引理1[22]考虑以下脉冲随机系统:

假设存在一个Lyapunov函数V(t,z(t))和满足对于任意t≥0,k ∈N都有φ(t,0)=ψk(0)=0的函数φ,ψk使得

1)对于t≥t0,存在正常数c1和c2使得c1∥z(t)∥≤V(t,x(t))≤c2∥z(t)∥;

2)存在连续函数φ:R+×R+→R,φ(t,s),对于任意t ∈R+在s上是凹的,使得LV(t,z)≤φ(t,V(t,z)),其中L定义如下:LV(t,z)=Vt(t,z)+Vz(t,z)ϕ(t,z)+trace(ηT(t,z)Vzzη(t,z));

则以下比较系统的平凡解的指数稳定性

表明了随机脉冲系统(2)的平凡解也是指数稳定的.

引理2[23]令φ(t)是一个连续函数,除了一些有限数量的点tk,其中φ()=φ(tk),φ()存在.定义集合为PC(l)={φ|φ:[-τ,∞)→Rl},0≤τ(t)≤τ.从序列PC(l),l=1中选取u(t),v(t).假设存在常数,和ς,使得

如果对于-τ≤t≤0有u(t)≤v(t),那么对于任意t>0,都有u(t)≤v(t).

随机Lur’e时滞耦合网络(1)的初始条件由zi(t)=ϕi(t),-τ≤t≤0,i=1,2,···,N所给出,其中ϕi(t)∈C([-τ1,0],Rn)是从[-τ1,0]到Rn的连续函数集.

为成功实现Lur’e网络的全局指数同步,本文设计提出如下的脉冲控制策略:

其中:µ代表脉冲效应;表示狄拉克脉冲函数,{t1,t2,t3,···}是一系列严格递增的脉冲序列.

随机Lur’e时滞网络考虑了控制器(4)后可调整为

3 随机Lur’e网络的全局指数同步

本节主要考虑由随机Lur’e时滞系统耦合而成的复杂动态网络(1)的全局指数同步问题.

首先,利用Kronecker积改写随机Lur’e网络(5)为

定理1考虑受控随机Lur’e网络(6)满足假设1,且假设定义1中脉冲序列ξ={t1,t2,···}的平均脉冲间隔小于Na.定义δ=(1+µ)2,有以下情形:

情况1对于δ >1,如果条件

那么具有时变时滞的随机Lur’e网络(1)在脉冲控制器(4)作用下将达到全局指数同步,其中:

证基于矩阵G上的Perron-Frobenius定理,构造如下Lyapunov函数:

通过考虑W的结构,得到

由-wij=ξiξj >0得知V(t)是一个非负函数.

对于t ∈[tk-1,tk),k ∈N,有

同时,根据假设2可知

因此,从式(12)–(14)可知

基于式(15)(21),考虑以下受控Lur’e网络(5)的比较系统(17),对于任意ϵ>0,都有唯一解γ(t),即

根据引理2 中的比较原理,可以得出,对于任何t >0有V(t) ≤γ(t).通过参数变分法,对于γ(t),t≥0,可以得到以下积分方程,其中包含时变时滞项γ(t-τ(t)),即

其中H(t,s)(t>s≥0)是以下线性脉冲系统柯西矩阵:

接下来,针对不同的脉冲效应µ取值范围,分别讨论随机Lur’e时滞网络的比较系统的同步情况.

情况1如果µ>0或者µ<-2即δ >1,通过运用平均脉冲间隔定义的右侧,可以计算出柯西矩阵

将方程(20)代入积分方程(18)得到

其次,将证明对于所有t ∈[0,+∞),都有

为了证明不等式(22)的有效性,本文将从数学的角度利用反证法.基于数学反证法,假设不等式(22)不是对所有t ∈[0,+∞)都成立,即至少可以找到一个时刻∈[t,+∞)使得

而不等式(22)对于t<,仍有

通过考虑式(21)(23)和λ-=0,可得

这与假设(23)相矛盾.因此,式(22)中的结论对于∀t ∈[0,+∞)都有效.

从而,令ϵ →0,那么有

根据定义1,可以得出以下结论:随机Lur’e时滞耦合网络(1)在脉冲控制器(4)的作用下可以实现全局指数同步.此外,可以计算出网络的收敛速度为λ,其中λ是方程λ-(p-)+(qeτλ)δN0=0的唯一解.

情 况2如 果-2 ≤µ<0 即0<δ≤1,通过运用平均脉冲间隔定义的左侧,可以计算出柯西矩阵为

同上可得

此外,对于t ∈[0],0<δ≤1,ϵ>0,λ′ >0,有

相应地,对于t ∈[0,+∞),由数学反证法可知式(28)成立.

令ϵ →0,那么有

比较系统(17)的平凡解是指数稳定的.根据定义1,可以得出以下结论:随机Lur’e时滞耦合网络(1)在脉冲控制器(4)的作用下可以实现全局指数同步.此外,根据比较原理可以计算出网络的收敛速度为λ′,其中λ′是方程λ′-(p-)+(qeτλ′)δN0=0的唯一解.

证毕.

注1在定理1中,基于比较原理和参数变分法,针对不同的脉冲效应,所对应的收敛速度是不一致的,脉冲效应决定了脉冲控制器的实际效果.网络的收敛速度与系统的时滞上限、脉冲效应强度、平均脉冲间隔和网络拓扑结构等密切相关,这与文献[24]中不同.另外,从收敛速度的结构以及λ的定义,可以发现当τ越小,其收敛速度越大,这意味着时变时滞的上限值τ直接影响随机耦合Lur’e网络的性能.

注2脉冲控制作为一种具有代表性的离散控制方法,可广泛应用于一些连续系统,从而有效降低控制成本.事实上,脉冲控制最显著的优点是控制效果只在非常稀疏的时间序列中被激活,在实践中被广泛使用,例如金融市场中的生态系统管理和货币供应控制等.在文献[25–26]等许多文献中,脉冲控制比连续控制更有效,甚至有时只有脉冲控制才能达到控制的目的.例如,计算机网络系统打补丁采取脉冲控制.

注3众所周知,现有大多数文献对脉冲效应的取值范围有一定的限制,从而导致在实际应用中利用脉冲信号进行控制有所限制,如文献[16–17].实际上,根据脉冲效应µ的不同取值,通常分别讨论3种脉冲,即同步脉冲、非活跃脉冲和去同步脉冲.首先,当脉冲效应满足-2<µ<0时,脉冲信号有利于动态网络的群聚行为[27];其次,如考虑到脉冲效应µ>0或µ<-2,此时脉冲可能会阻碍甚至破坏受控网络的同步[28];最后,对于特殊的脉冲效应µ=-2以及µ=0,脉冲对受控网络的性能既无害也无利[20].

注4为实现Lur’e网络的全局指数同步,文献[29]等以往的工作主要采用脉冲控制和Halanay不等式的方法,而文献[30]则设计了一个单牵制脉冲控制器并同时使用Lyapunov方法.然而,本文将比较原理和参数变分原理运用于脉冲控制下复杂网络系统中,简化了证明过程,算出收敛速度.

注5在现有的大多数复杂网络同步研究中,不可避免地设置了参考系统或目标系统.例如,文献[8]等诸多文献均提出了目标系统˙s(t)=f(s(t)),其中s(t)由于同步∥zi(t)-s(t)∥→0(t →+∞)的定义,一直被选为孤立系统的状态向量.此外,在文献[21]中选择了一个虚拟目标点作为参考系统,并且可以通过定义误差向量ei(t)=zi(t)-得出结论.事实上,为耦合网络设置目标系统可能会导致系统资源的浪费,并使分析过程更加繁琐.为此,本文通过充分考虑Perron-Frobenius定理,设计一种新颖的Lyapunov函数,提出了无参照系统策略,从而实现该复杂网络的无参照、无目标全局同步.

4 数值仿真

为验证本文所提出全局指数同步判定方法和控制器设计方案的有效性,在此仿真中采用蔡氏振荡电路耦合的复杂动态网络的两个例子进行说明.

考虑以下具有随机扰动和时变时滞的蔡氏电路:

其中系统状态方程形式如下:

因此,定理1中的条件可以满足.从图1可以发现,随着时间的推移,随机Lur’e系统的每个状态的轨迹曲线都趋近于一致,即进一步意味着随机耦合Lur’e网络的全局指数同步最终在所提出的具有脉冲效应µ=0.6的脉冲控制策略下实现.

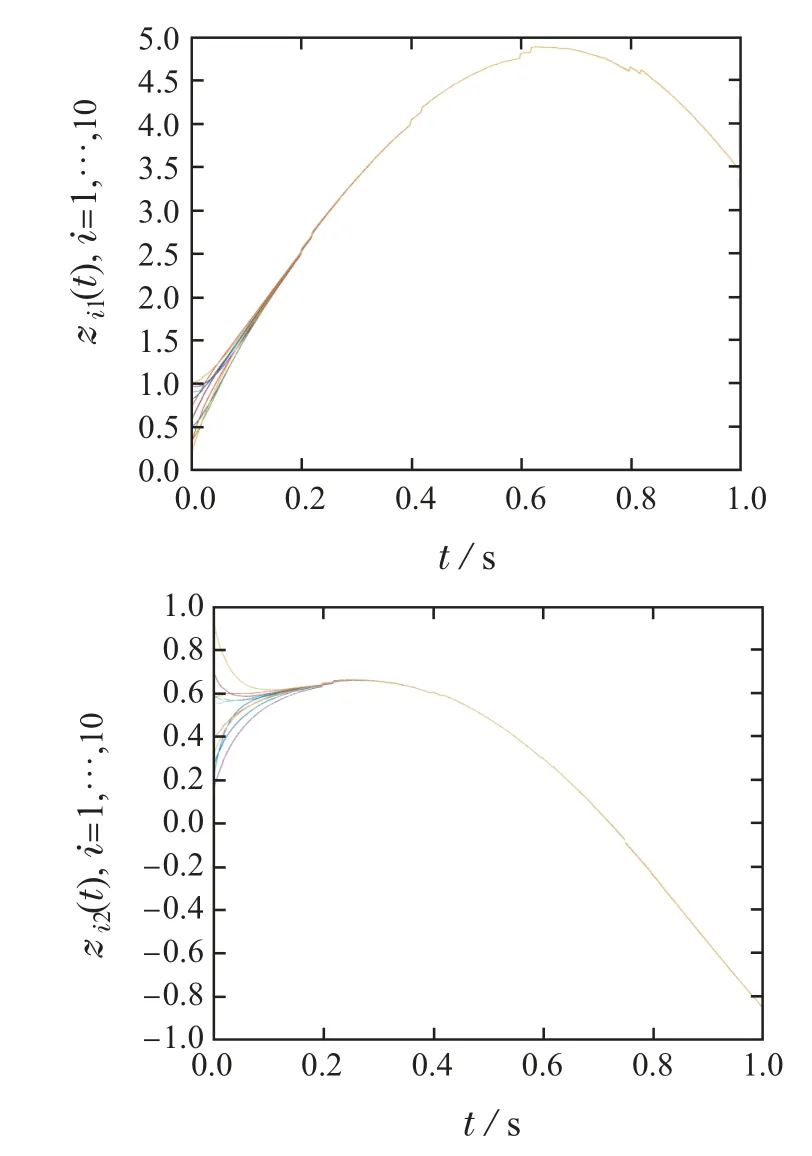
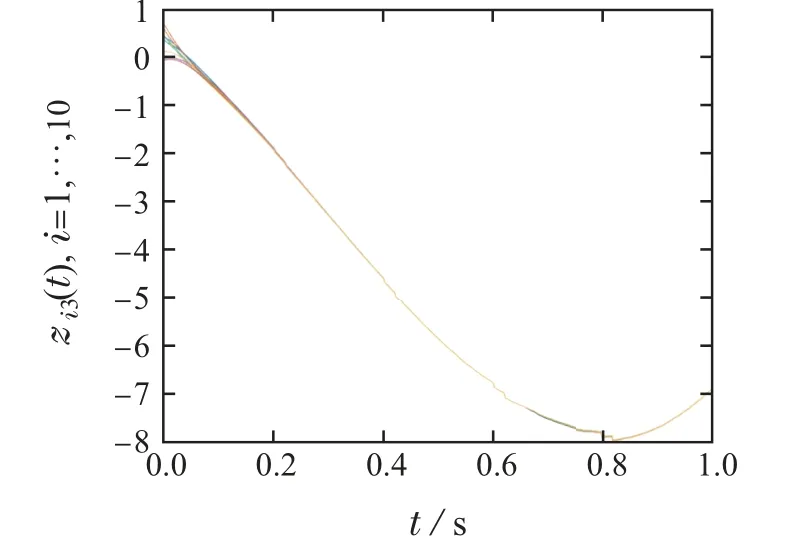
图1 脉冲效应µ=0.6 时耦合动态网络状态轨迹zi(t),i=1,···,10Fig.1 State variables zi(t),i=1,···,10 of the coupled dynamical network with impulsive effectµ=0.6

例2对于定理1的第2种情况,选取µ=-0.6.同样地,可以计算出γ=2.5,p=68.6,q=15.7,-p+qδN0<0.因此,定理1中的条件可以满足.

由图2可知,随机Lur’e系统之间的全局指数同步可以在脉冲效应为µ=-0.6的脉冲控制策略下实现的.

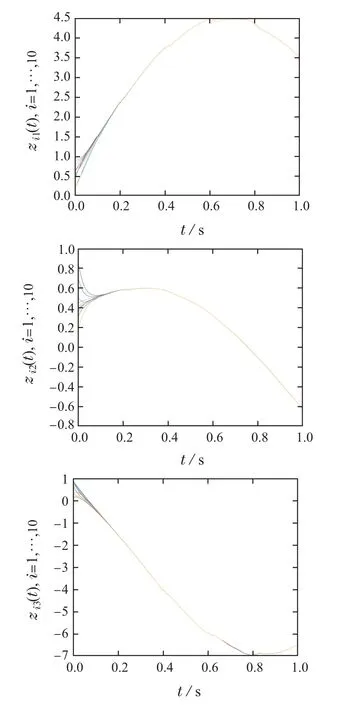
图2 脉冲效应µ=-0.6时耦合动态网络状态轨迹zi(t),i=1,···,10Fig.2 State variables zi(t),i=1,···,10 of the coupled dynamical network with impulsive effectµ=-0.6

5 结论

本文通过提出一种有效的脉冲控制策略,讨论了一类具有不对称耦合和时变时滞的随机Lur’e动态网络的全局指数同步问题.基于平均脉冲间隔、无参照系统策略、比较原理和参数变分原理,给出了随机Lur’e网络全局指数同步的判定条件.此外,考虑到不同功能的脉冲效应,可以准确地获得不同的收敛速度.从证明过程可以看出,网络同步判定条件对脉冲间隔的上下界没有具体要求,下界可以无限小,上界可以很大,大大降低了同步标准的保守性.最后,给出了脉冲效应不同取值的数值仿真来说明主要结果的合理性和控制策略的有效性.