全方位机器人的重心位置预测与轨迹跟踪控制
王义娜 ,刘赛男 ,王硕玉 ,杨俊友
(1.沈阳工业大学电气工程学院,辽宁 沈阳 110870;2.高知工科大学智能机械系,日本 高知 7828502)
1 引言
与传统的移动机器人相比,全方位移动机器人具有以同一姿势向各方向移动的优点,在工业、医学和航空航天领域应用广泛,如搬运机器人[1]、步行训练机器人[2]等.但是由于货物放置位置不同、被辅助者姿势发生变化会导致机器人重心产生偏移,进而影响机器人的轨迹跟踪精度.为了进一步提高机器人的轨迹跟踪精度,实时估计并预测重心位置具有重要作用.
全方向移动机器人属于动态非线性强耦合系统,因此其跟踪控制尤其是针对重心偏移的路径跟踪控制问题比较难.目前国内外学者针对此问题的研究主要集中于解决机器人的参数不确定性和外部扰动问题以提高其跟踪精度[3–14],其中包括基于分层改进算法的模糊动态滑模控制[3]、基于扩展状态观测器的积分滑模控制[4]、模糊控制[5]、基于扰动观测器的滑模控制[6]、基于极坐标的自适应控制[7]、基于双鲁棒控制器切换的控制算法[8]、自抗扰控制[9]、自抗扰反步控制[10]以及基于扰动观测器的滑模控制[11]等算法.其中,文献[3–6]是面向双轮移动机器人而并非全方向移动机器人,文献[7–11]研究未考虑重心偏移问题.另外,有些研究者基于模型预测控制展开研究[12–16],其中包括基于线性扩展状态观测器的模型预测控制[12]、具有控制约束的模型预测控制[13–14]以及应用摩擦补偿的模型预测控制[15–16]、应用重心偏移补偿的模型预测控制[17].这些控制算法可在满足约束条件下减小重心偏移对跟踪精度的影响,然而都未直面重心偏移引起的动态耦合矩阵不确定问题进行处理,不能完全解决重心偏移对跟踪精度的影响.文献[18]提出一种基于多转子混合矩阵的估计法,对重心偏移产生的位置漂移进行补偿,文献[19]基于神经网络对机器人重心位置进行估计,并结合自适应加权数据融合算法获得其最终重心位置,然后通过反向动力学模块对其进行运动控制.然而,文献[18–19]的研究对象均为飞行机器人.专门针对全方位移动机器人重心偏移问题的路径跟踪控制方法包括具备参数辨识功能的自适应控制法[20]及基于统计对比模型的自适应跟踪控制[21],然而文献[20]中控制器的稳定性建立在重心位置变化较慢的基础上,另外,文献[21]中统计对比模型限制项较多,很难满足要求.文献[22]通过将重心偏移对绕重心转矩的影响转换到机器人的惯性矩阵中,通过最小二乘法在线辨识惯性参数,来补偿重心偏移影响.然而,该方法辨识的惯性补偿项是重心偏移引起的偏差项,存在滞后性.现有的基于数据驱动建模的重心偏移参数估计法在实时控制问题中应用研究较少,且存在滞后性,对估计结果做进一步预测,可提高控制时效[23–24].
针对以上问题,本文提出了一种基于数据驱动的系统建模法及基于重心参数预测的轨迹跟踪控制法,主要贡献归纳如下:
1)建立机器人考虑重心偏移的动力学模型,针对实时重心偏移问题,应用长短期记忆(long short-term memory,LSTM)神经网络构建其对比模型,并基于数据驱动法对重心偏移参数进行估计,再基于张神经网络(zhang neural network,ZNN)对估计参数进行预测,可解决估计滞后性的影响;
2)针对非线性动态强耦合问题,提出基于动态非线性反馈解耦法及数值加速度控制法的机器人轨迹跟踪控制算法,保证控制系统稳定的同时实现机器人的高精度跟踪.
2 OWTR及其动力学建模
本论文将以本实验室所开发全方位步行训练机器人(omnidirectional walking training robot,OWTR)为研究对象.如图1所示,OWTR的四角底部安装了4个全向轮,以实现全方向移动.OWTR的扶板内安装了6个压力传感,以检测使用者附加在扶板上的压力.扶板前方安装了触摸屏,以作为人机交互接口,可供使用者选择OWTR的多种训练模式.另外,机器人还设计了多重安全保护措施,如:防后倾支撑结构、防坠坐垫与急停按钮,以保证使用者的安全.
OWTR宽0.93 m,长1.03 m,自重为80 kg,最大负荷为80 kg,其扶板高度从0.9 m到1.2 m可调,以适应不同高度的训练者.
为简化分析,本论文将OWTR当成刚体并假设其受力及运动在同一二维水平面内.当使用者借助机器人行走时,由于姿势及步态的改变,会导致机器人的重心位置实时变化.因此,建立其二维坐标系内分析图如图2 所示.其中:Σ(X,O,Y)为地球坐标系;Σ(xR,C,yR)为机器人坐标系;C为机器人中心位置;G为机器人重心位置,且重心偏移量可由r与α来描述,r为中心到重心间距离,α是CG相对于姿势角的角度;θ为机器人姿势角,定义为第1个全向轮同中心连线与x轴之间夹角;V指机器人的速度;β为机器人的移动方向,指V方向相对x轴的夹角,根据图2所示受力情况,vi为第i个轮子的速度;l是机器人中心到4个全向轮的距离;fi指第i个全向轮所受驱动力;li指机器人重心到第i个驱动力的力臂,i=1,2,3,4.如图2所示,当存在重心偏移时,各力臂长度会随重心位置的变化而变化,从而影响绕重心位置的转矩,另外还会引起机器人转动惯量的变化,进而影响运动性能.因此设计控制输入时,需要得到重心位置到各驱动力的距离,以消除重心偏移对运动精度的影响.
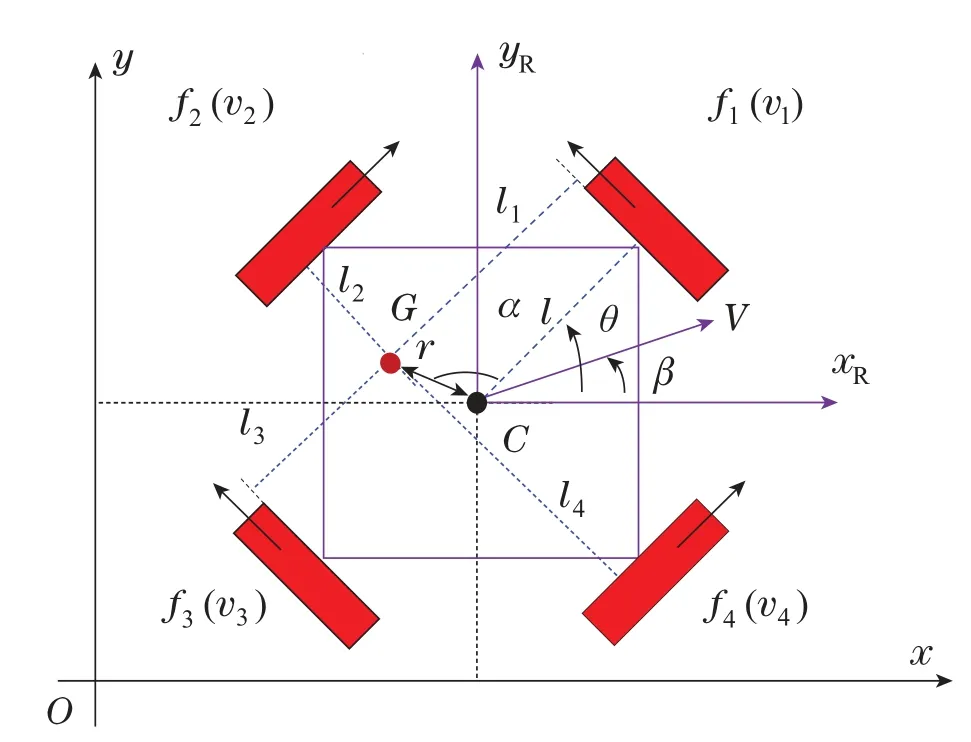
图2 机器人受力及运动分析图Fig.2 Force and motion analysis of robot
接下来本文将基于图2建立机器人的非线性运动学及动力学模型.首先,建立机器人中心位置的运动学模型如下所示:
其中:M为机器人质量,m为人附加给机器人的等价质量,I为机器人的转动惯量,mr2为重心偏移引起的附加转动惯量,,为机器人重心位置在x方向与y方向的加速度,为机器人旋转的角加速度.
在实际运行中,笔者更希望高精度控制机器人的中心位置,因此,需建立其中心位置的动力学模型.将等式(2)代入式(3)可得机器人重心处加速度和中心处加速度之间的关系如下:
最后,根据重心位置动力学模型(3)及重心与中心位置加速度关系(4),建立机器人中心位置的动力学模型如下:
由此动力学模型(5)可以看出,于重心与中心位置相对运动关系会产生一个切向力和法向力而影响相互运动,即出现扰动项MG影响中为位置的运动,该扰动项同样会随重心位置(r和α)的变化而变化.
3 控制器设计
本节针对具有重心偏移干扰和摩擦干扰的机器人系统,设计了一种考虑重心偏移的数值加速度控制方案.通过一种基于LSTM神经网络训练对比模型,根据对比模型到达的位置和机器人实际位置之间的差值估计重心参数,然后采用张神经预测求逆网络进行参数预测并将结果引入控制律,控制系统结构框图如图3所示.
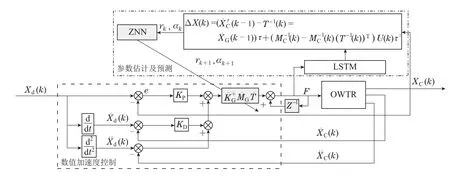
图3 带有参数估计及预测的数值加速度控制系统Fig.3 Digital acceleration control system with parameter estimation and prediction
3.1 考虑重心偏移的数值加速度控制方案
首先,基于文献[22]所提数值加速度控制算法,通过将式(5)所示机器人动力学模型以采样周期τ进行离散化,设计包含非线性状态反馈的OWTR数值化加速度控制器,其表达式如下:
3.2 重心偏移量在线估计
由于式(6)中非线性状态反馈矩阵中不确定项和机器人实时重心偏移量(rk和αk)相关,故本节引入一个新的参数估计法实时估计当前时刻重心偏移量(和),从而得到式(6)中非线性状态反馈矩阵,的值.该参数估计法可由机器人4个轮子受到的驱动力和实时位置输入得到机器人实时重心偏移量的估计值.
给定对比模型和实际模型相同驱动力F(k),U(k)=KC(k)F(k)为对比模型3个方向上的扭矩值,由对比模型和实际机器人之间的位置差∆X(k)=(k)-XC(k)与当前时刻的重心偏移量关系建立如下等式:
式中除矩阵MG和T中含有未知的重心偏移参数rk,αk,其余量均为已知,故采用牛顿迭代法解方程(7)可对重心偏移量进行估计.
方程(7)可由以下步骤得出:
步骤1建立对比机器人模型k时刻位置(k)和4个全向轮上的驱动力F(k)关系式为
步骤2建立有重心偏移机器人模型k时刻位置和4个全向轮上的驱动力F(k)关系式为
式中:XC(k-1)为t=(k-1)τ时刻XC的值,(k-1)为t=(k-1)τ时刻˙XG的值,KG(k)为t=kτ时刻KG的值.
步骤3将式(8)–(9)做差,即可得到式(7).
3.3 基于LSTM建立对比模型
式(7)成立的前提为对比模型除没有重心偏移影响外,其余摩擦等干扰均和实际机器人保持一致.故在实际应用中建立对比模型时需要考虑机器人行走过程中受到的干扰情况.对比模型通过LSTM神经网络进行预训练使其接近理想的对比模型.
LSTM神经网络是一种以LSTM细胞为隐层的递归神经网络(recursive neural network,RNN),原理图如图4所示,用公式表示如下:

图4 LSTM神经网络原理图Fig.4 Schematic diagram of LSTM neural network
LSTM单元的输入是t=kτ时刻对比模型4个轮子驱动力F(k),通过式(13)–(17)得到LSTM输出:t=kτ时刻对比模型的位置(k).LSTM神经网络可以提取隐藏的自然结构和抽象特征,且具有非线性拟合能力,确保基于该神经网络建立的对比模型能有效估计出重心偏移参数.
3.4 重心偏移量预测
为了克服重心偏移量的影响,需要实时估计当前时刻的重心偏移量并提前进行补偿,参数估计部分只能估计出上一时刻的重心偏移量,具有滞后性.为了解决这个问题,本文采用文献[24]中的ZNN预测求逆方法对矩阵KG进行预测求逆,进而预测下一时刻的重心偏移量.ZNN预测求逆原理图如图5所示.

图5 ZNN预测求逆原理图Fig.5 Schematic diagram of ZNN prediction inversion
由图5可得连续时间ZNN预测求逆公式如下:
采用四阶有限差分公式近似离散KG的一阶导数,即
由式(16)–(17)可得k+1时刻值如下:
其中:h=λτ为预测参数,其决定着重心参数估计的速度及精度;由k+1时刻的值可得k+1时刻重心偏移量.
3.5 稳定性分析
定理1假设系统重心偏移参数有界,则系统矩阵KG的弗洛贝尼乌斯(Frobenius)范数∥KG∥F有界,采用式(18)预测KG的广义逆矩阵并得到重心偏移参数,假设式(16)所示的五阶差分截断误差为o(τ3)及式(17)所示的四阶瞬时后向有限差分截断误差为o(τ3)时,利用预测参数h,使预测参数趋近真实值,估计值且截断误差阶为o(τ4),最大参数估计误差为τ4,因此保证了闭环系统的稳定性.
证 为抑制因KG中含有重心偏移参数的项时变导致其广义逆矩阵不确定而产生的影响,使用式(18)对进行估计,将其代入KG求逆误差公式的Frobenius 范数中,由式(8)(17)得其截断误差各为o(τ3)可得
定理2对于考虑重心位置实时变化的OWTR动态模型(式(5)),在控制输入(6)作用下,当控制参数满足以下约束条件时:
证首先,建立OWTR动态模型(式(5))在时间区间[(k-1)τ+,kτ]边缘时刻的离散化动力学模型为
将控制输入(6)代入离散化动力学模型(20)–(21)中,并定义控制系统kτ+时刻的跟踪误差为
其中:XC(kτ+)为t=kτ+时刻机器人的实际位置.Xd(kτ+)为t=kτ+时刻机器人的目标位置,将跟踪误差(17)代入式(20)–(21)与式(6)构成的OWTR离散化闭环控制系统中,可得系统跟踪误差离散化动力学模型为
4 仿真验证
通过仿真验证本文提出的带有参数估计及预测的数值加速度控制器的有效性.仿真中对比模型采用长短期记忆网络进行训练,先使机器人空载按预定的轨迹移动,记录4个轮子的控制输入与当前位置数据,采用长短期记忆神经网络进行训练,训练结果作为对比模型,训练结果如图6所示.由图6可知,在无外部干扰情况下LSTM神经网络可准确近似与理论对比模型,由此可知实际应用中,LSTM神经网络也能很好的逼近实际机器人的对比模型.

图6 神经网络训练结果图Fig.6 Neural network training results
为了验证本文所提参数估计及预测方法的有效性,分别与文献[20]所用自适应控制器及文献[22]所提数值加速度控制器进行了仿真对比分析.自适应控制器参数为:Γ=diag{110,110,110},λ=diag{30,25,16},K=diag{140,140,6}.采样时间为τ=0.04 s.两个数值加速度控制器参数为:KP=diag{20,20,20},KD=diag{10,10,10}.重心参数估计与预测参数λ=0.3.
OWTR 初始位置设为XC0=[0 0.2 0]T,仿真时间为20 s,未知重心偏移参数设计如下:r=0.2+0.15 sint,α=0.02t,期望轨迹为
机器人的仿真结果如图7 所示,运动路径如图7(a)所示.由图7(b)可知,数值加速度控制的跟踪误差:x轴16 s 后才收敛至0.010 m,y轴17 s 后才收敛至0.011 m,θ也需17 s以上才收敛至0.827 rad.自适应控制的跟踪误差:x轴在4 s 内收敛至0.009 m,y轴用不到3 s 收敛至0.012 m,θ需13 s 以上收敛至0.280 rad.本文所提控制算法的跟踪误差:x轴由1 s 内收敛至0.004 m以下,y轴用不到1.5 s收敛至0.00 5m以内,θ用不到1.5 s收敛至0.038 rad 以内.相对于数值加速度与自适应控制器,本文所提控制算法跟踪误差更小,响应时间更快.表明所提控制算法由图7(c)所示,估计值t12,t13在4 s内即可逼近于真值,稳定后估计误差绝对值保持在0.001范围内,验证所提算法能正确估计重心偏移参数量.


图7 轨迹跟踪仿真效果对比Fig.7 Comparison of simulation results of trajectory
进一步以绝对误差积分(integral absolute error,IAE)作为评价标准,对3种控制器效果进行量化对比分析.IAE定义如下:
由3种控制器的量化对比结果表1所示,相对于自适应控制器与数值加速度控制器,本文所提算法的IAExy分别减小了4 m和6 m,IAEθ分别减小了118 rad和391 rad,控制性能有显著提高,尤其是相对于数值加速度控制增加了重心偏移参数估计以后跟踪效果明显增加,验证所提控制算法有效性.

表1 仿真环境下控制器性能对比Table 1 Comparison of controller performance in simulation environment
5 实验与结果
为进一步考察所提控制算法在面向步行训练机器人实际应用中的有效性,本节将在实验室环境内对机器人进行路径跟踪实验.实验环境如图8所示,采用超宽带(ultra wide band,UWB)定位技术进行位置检测,为避免遮挡问题,标签芯片由支架支撑并放置在机器人正上方,检测的位置数据发送给电脑,并基于Python进行控制力计算并以频率为25 Hz信号发送给机器人.机器人跟踪目标路径为C型,负载为1名23岁健康男性模拟腿部残疾者借助机器人行走,其在行走中对机器人的扶板施加较大负重(包括推力和压力),会显著引起重心位置变化且实时变化.

图8 实验环境图Fig.8 Experimental environment diagram
5.1 训练对比模型
本小节基于LSTM神经网络基于实验数据建立机器人的对比模型.具体过程为:先使机器人在空载条件下以设定轨迹进行移动,并实时记录所发送控制输入与所测当前位置,共采集500个时间序列共3500个点作为训练数据;然后基于LSTM神经网络,以所发送控制力为输入,传感器所测相应位置数据为输出,对所建立对比模型(8)进行训练,其神经网络输入输出数据如图9–10所示.

图9 各个轮子上的驱动力Fig.9 Driving force on each wheel

图10 机器人在x轴、y轴方向上位置的变化量Fig.10 Variation of robot position in x-axis and y-axis directions
5.2 轨迹跟踪实验及结果
C型路径的目标轨迹如下所示:
采用文献[22]中数值加速度控制器以及文献[17]中的模型预测控制器和本文所设计的控制器进行对比实验,实验结果如图11所示.文献[17]控制器的参数如下:R=diag{0.2,0.1,0.1,0.2},Q=diag{1.3,1.5,0.2}.文献[22]及本文所用数值加速度控制器参数如下:kpx=1.2,kpy=1.2,kpθ=1.2,kdx=8,kdy=8,kdθ=8.本文重心偏移估计参数及初始值如下:λ=0.3,=0,=0.

图11 实验机器人跟踪结果图Fig.11 Experimental robot tracking result diagram
由图11可以看出,本文所设计的控制器相对于文献[22]中所设计的数值加速度控制及文献[17]中所设计的模型预测控制相比,其控制精度更高.为进一步分析所提算法的效果,本文对图11所示跟踪结果进行量化分析,如表2 所示,MAD 表示其平均绝对误差(mean absolute deviation),MAX表示最大值.由表2可看出,本文所提算法比数值加速度控制器的跟踪误差减小0.58 m,比文献[17]采用的模型预测控制跟踪误差减小0.1027 m.

表2 实验环境下控制器性能对比Table 2 Comparison of controller performance under experimental environment
综上所述,针对重心偏移干扰下全向移动机器人轨迹跟踪控制问题,含有重心偏移参数估计及预测的数值加速度控制器具有良好的鲁棒性,机器人可以较为快速精确地跟踪期望轨迹.实验结果验证了含有重心偏移补偿控制算法的有效性.
6 结论
本文针对全方位移动机器人运动过程中重心偏移不确定性问题,提出了基于动力学模型的移动机器人重心偏移参数估计及预测的数值加速度轨迹跟踪控制方法.推导了含有重心偏移干扰的动力学模型,提出了一种新型参数估计法对重心偏移量进行实时估计并通过ZNN求逆算法进行预测,然后通过数值加速度控制器对其进行实时控制.仿真及实验结果表明,在重心偏移参数未知且变化的情况下,该方法能够通过当前位置估计出参数真实值,使得位置偏差收敛到参考轨迹,且相对于数值加速度与自适应控制器而言跟踪精度有显著增加.

