融合改善型可行性检验模型的换道跟踪方法

向云丰，贺岩松，孔伟伟，陈 健，罗禹贡

(1.重庆大学 汽车工程学院， 重庆 400044;2.清华大学 汽车安全与节能国家重点实验室，北京 100084)

近年来无人驾驶技术不断发展，自主换道是其中重要的技术组成部分[1]。自主换道[2-3]由换道决策[4]、换道轨迹规划[5]和换道轨迹跟踪[6]三部分组成。换道决策决定是否执行换道[4,7]，包括换道意图、换道目标车道选择和换道可行性检验。换道可行性检验作为是否执行换道的最后关卡，其完备性直接影响换道的安全性，换道轨迹跟踪是无人驾驶汽车运动控制的核心所在。因此对换道可行性检验和换道轨迹跟踪进行研究是极其重要的。

张帅[3]提出了一种换道可行性检验模型，模型中考虑了本车距本车道前后车辆和目标车道前后车辆的最小安全距离。王文霞[8]推导了换道车辆与周围车辆应满足的起始最小纵向安全距离。张荣辉等[9]推导了车辆换道汇入车队前与车队中汇入点前、后车辆的最小安全距离。王政[10]使用换道车辆与目标车道前后车辆的间距大于最小安全距离作为换道的可行性条件。以上模型均假设周围车辆处于车道保持状态，未考虑周围车辆换道对本车换道可行性的影响。

综上所述，现有的换道可行性检验模型往往假设周围车辆处于车道保持状态，且只考虑本车道和目标车道前后车辆的影响。在轨迹跟踪方面，现有的很多跟踪器不能求解带约束的问题。针对上述问题，重点研究全面考虑周围车辆影响的换道可行性检验模型和轨迹跟踪控制方法。

首先分析车道变换的逻辑架构，然后充分考虑处于不同车道和不同状态的周围车辆对本车换道的影响，推导改善型的换道可行性检验模型，其次使用能求解带约束问题的MPC控制器进行换道轨迹跟踪，最后设计仿真对比试验，对所研究的模型和方法进行验证。

1 车道变换逻辑架构

通过分析驾驶员的换道过程，建立车辆自动换道逻辑架构，如图1所示。根据换道逻辑架构，需要建立换道意图产生前的跟车模型、驾驶员是否对当前车道满意的换道意图模型、执行换道前的目标车道选择模型和换道可行性检验模型、换道过程中的换道轨迹规划模型和换道轨迹跟踪模型。

图1 车道变换逻辑架构Fig. 1 Logic framework of lane-changing

在跟随前车过程中，采用Gipps安全距离模型[20]进行纵向速度控制。Gipps安全距离模型由两部分组成:加速子模型与减速子模型。通常将两者同时计算出来，跟驰速度取较小者。

加速子模型：

(1)

减速子模型：

(2)

在换道意图方面，使用文献[3]中的驾驶员不满意度pk表示本车对换道的渴望程度。计算公式如下：

(3)

式中：Yu为驾驶员不满意度阈值；kf∈{0,1,2,3}为本车道前方车辆的种类，0,1,2,3分别代表无车、事故车辆或施工造成的静态障碍区、商用车、乘用车；lf为本车距离前车的纵向距离；lsafe为最小跟车安全距离[20]，其大小与实际车速vs(单位：m/s)相关；ax为纵向加速度。根据文献[3]取Yu=500，当pk≥Yu时，无人驾驶汽车产生换道意图，需进行目标车道选择。

lsafe=0.002 9(vS×3.6)2+0.304 9(vS×3.6)。

(4)

使用文献[3]中的最大安全速度V(单位：m/s)进行车道选择。将本车道与左右两车道的最大安全速度对比，最大安全速度值最大的车道即为目标车道，若本车道最大安全车速最大，则继续跟随前车，等待换道时机。

(5)

2 换道可行性检验模型

在三车道高速公路场景中，按照换道车辆所处车道的位置可将换道场景分为中间车道车辆换道场景(如图2)和边缘车道车辆换道场景(如图3)。两类换道车辆的差别在于是否可能存在相间车道的车辆向目标车道换道(如图3中最左侧车辆可以向本车的目标车道换道)。

图2 中间车道车辆换道场景Fig. 2 Lane-changing scene of the vehicle in the middle lane

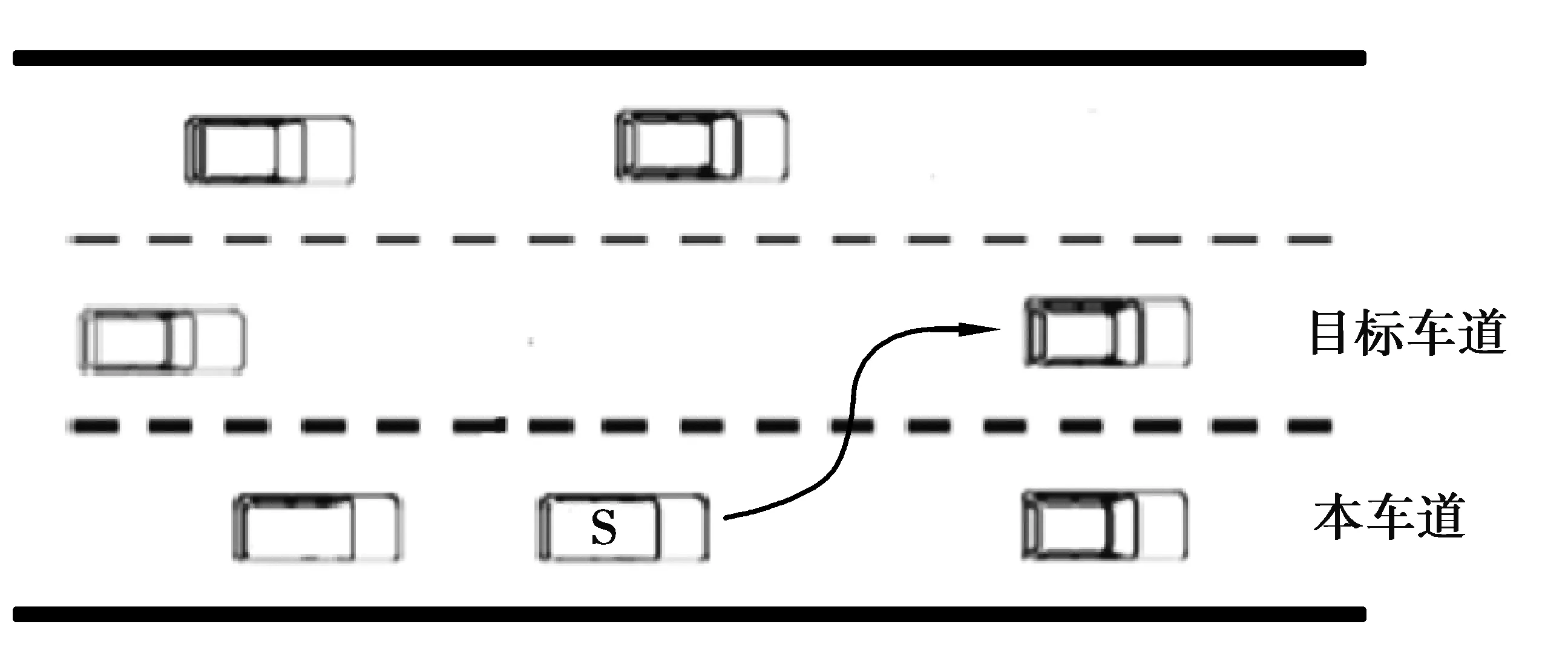
图3 边缘车道车辆换道场景Fig. 3 Lane-changing scene of the vehicle in the edge lane

2.1 中间车道车辆换道可行性检验

对于中间车道车辆换道场景，非目标车道(如图2中的右车道)的车辆如果处于换道状态，其换道前已经对周围车辆进行了换道可行性检验，即其与本车距离较大；且本车换道的横向运动方向与非目标车道相反，所以非目标车道的车辆换道与否不会影响中间车道车辆的换道。同理，不需要考虑本车道前后车辆往非目标车道换道。因此只需要讨论其他情形下本车道前后车辆和目标车道前后车辆对本车换道的影响。

2.1.1 目标车道前车可行性检验

当目标车道前车处于车道保持状态时，假设目标车道前车沿车道中心线行驶。如图4所示，定义本车S的左上角第一次触碰目标车道前车边线LFt时的点为C点，则该点为本车S与目标车道前车Ft的临界碰撞点，定义该时刻为tC。即在本车左上角未到达边线LFt之前(0～tC)，本车不会与目标车道前车发生任何形式的碰撞。在tC～T(设换道结束时刻为T)，如果本车最前点(左前点或者右前点)在目标车道前车最后点之后，本车不会与目标车道前车发生任何形式的碰撞。即：

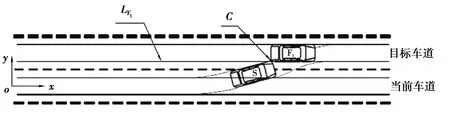
图4 本车与Ft的碰撞示意图Fig. 4 Collision diagram of Ft and S

(6)

式中：xS(t)、xFt(t)分别为t时刻本车和目标车道前车的纵向位置；θ为本车车头方向与水平方向的夹角；lS与lFt分别为本车和目标车道前车长度；wS为本车宽度。下标S、Ft、Rt、Fp、Rp、Fi和Ri分别表示本车、目标车道前车、目标车道后车、本车道前车、本车道后车、相间车道前车和相间车道后车。cos(θ(t))≤1，|sin(θ(t))|≤max|sin(θ(t))|，因此，∀t∈(tC,T)，若满足(7)式，则(6)式成立。

(7)

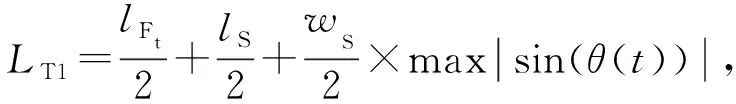
(8)

(9)

若

DFt(0)≥lFt，

(10)

则本车不会与目标车道前车发生任何形式的碰撞。

由于本车在对比本车道和目标车道的速度优势后，选择向目标车道换道，因此目标车道前车只可能向本车道前车前面换道，不可能往本车前换道。当目标车道前车处于车道变换状态时，其离本车道前车有一定的安全距离，离本车的距离更大，所以目标车道前车的换道状态不会影响本车换道的可行性。因此只需满足式(10)，则本车不会与目标车道前车发生碰撞。

2.1.2 目标车道后车可行性检验

本车横向位置处目标车道的最优车速大于本车道，目标车道后车处最优车速更大，所以目标车道后车不会选择往本车后面变道，只需考虑目标车道后车处于车道保持状态。与目标车道前车一样，本车左上角未到达目标车道后车边线LRt前(0～tC)，本车不会与目标车道前车发生任何形式的碰撞。同理定义：

DRt(0)=xS(0)-xRt(0)-LT2，

(11)

(12)

若

DRt(0)≥lRt，

(13)

则本车不会与目标车道后车发生任何形式的碰撞。

2.1.3 本车道前车可行性检验

当本车道前车往本车的目标车道换道时，如果本车继续换道，仍然跟随的是目前的前车，换道完成后驾驶员不满意度仍然很大，因此此时本车不进行换道，等待前车换道完成后再决定是否换道。

当本车道前车处于车道保持状态时，定义本车S的右上角第一次触碰本车道前车右边线LFp的点为C1点(见图5)，则该点为本车S与本车道前车的临界碰撞点，定义该时刻为tC1。即在本车右上角未到达边线LFp之前(0～tC1)，本车可能与本车道前车发生正碰或者角碰。在tC1～T本车不会与本车道前车发生任何形式的碰撞。

图5 本车与Fp的碰撞示意图Fig. 5 Collision diagram of Fp and S

定义

DFp(0)=xFp(0)-xS(0)-LT3。

(14)

(15)

DFp(0)≥lFp，

(16)

则本车不会与本车道前车发生任何形式的碰撞。

因此若本车道前车往本车目标车道变道，则本车放弃变道，等待前车换道完成之后再确定是否变道；其他情形下，只需满足(16)式时，本车道前车不会影响本车换道。

2.1.4 本车道后车可行性检验

当本车道后车处于车道保持状态时，如图6所示，定义本车S的右下角第一次触碰本车道后车右边线LRp时的点为C2点，则该点为本车S与本车道后车的临界碰撞点，定义该时刻为tC2。同理定义：

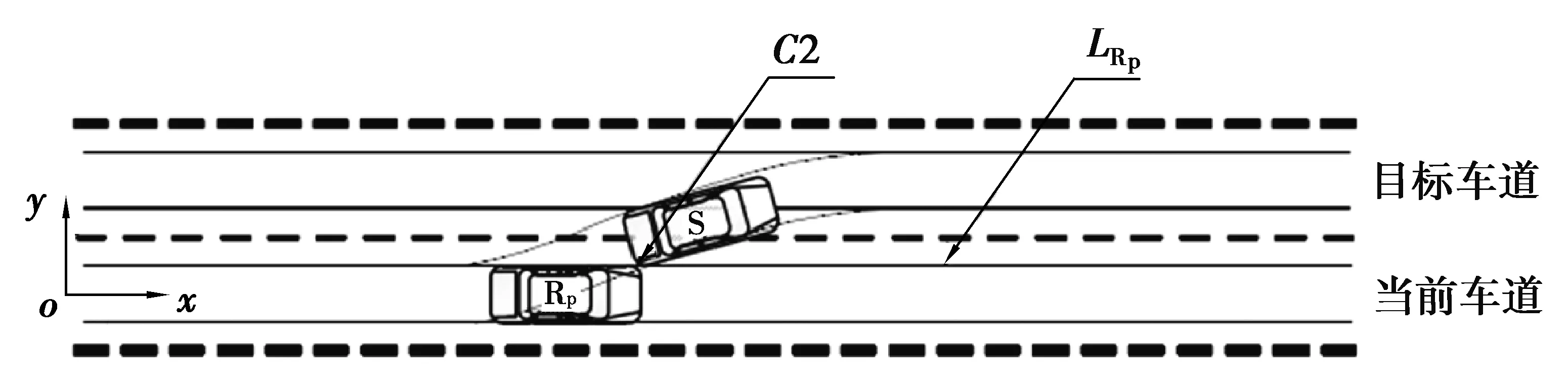
图6 本车与Rp的碰撞示意图Fig. 6 Collision diagram of Rp and S

DRp(0)=xS(0)-xRp(0)-LT4。

(17)

(18)

若

DRp(0)≥lRp，

(19)

则本车不会与本车道后车发生任何形式的碰撞。

当本车道后车往目标车道变道，为了确保换道安全，可使本车的最后点在本车道后车最前点之前，即

(20)

式中：θ1为本车道后车换道过程车头方向与水平方向的夹角；wRp为本车道后车的宽度。

由cos(θ(t))≤1,|sin(θ(t))|≤max|sin(θ(t))|，cos(θ1(t))≤1，|sin(θ1(t))|≤max|sin(θ1(t))|，可使

(21)

定义

DR1p(0)=xS(0)-xRp(0)-LT41。

设(0,T)时间段内本车道后车与本车之间最大相对纵向位移为：

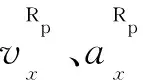
若

DR1p(0)≥lR1p，

(22)

则本车不会与本车道后车发生任何形式的碰撞。

本车可以根据周围车辆转向灯信息判断周围车辆是否想换道，且能判断往哪一方向换道。如果本车处于中间车道，可以根据图7的逻辑判断流程图检验车辆换道可行性。

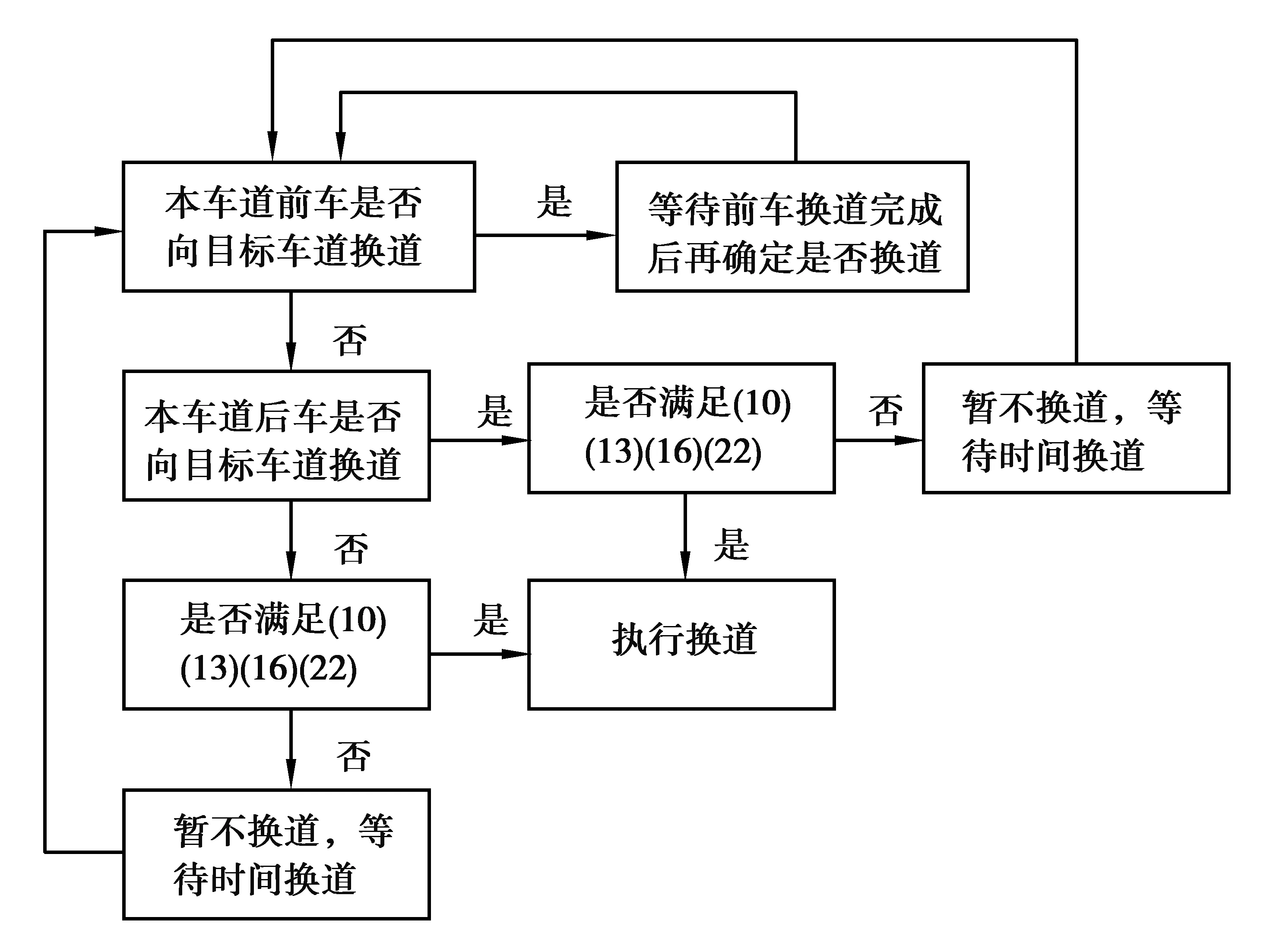
图7 中间车道换道可行性检验流程图Fig. 7 Flow chart of lane-changing feasibility test in the middle lane

2.2 边缘车道车辆换道可行性检验

对于边缘车道的车辆，除了受本车道车辆和目标车道车辆影响外，还会受到相间车道车辆换道的影响。如图3所示，当本车S想要往目标车道换道时，如果相间车道车辆也往目标车道换道，则本车S与相间车道车辆可能在目标车道发生碰撞，因此必须讨论相间车道的车辆对本车换道的影响，确保换道安全。

2.2.1 相间车道前车可行性检验

当相间车道前车向目标车道变道时，本车左上角达到目标车道边界线前(临界点C3)，本车不会与相间车道前车发生碰撞。在tC3～T，为了确保换道安全，只需使本车的最前点在相间车道前车最后点之后，即

DFi(0)≥lFi，

(23)

式中：DFi(0)为换道前本车与相间车道前车的初始纵向距离，lFi为(tC3,T)时间段内本车与相间车道前车之间最大相对纵向位移。

DFi(0)=xFi(0)-xS(0)-LT5；

式中：xFi(0)为换道前相间车道前车纵向位置，wFi相间车道前车宽度，θ2为相间车道前车换道过程车头方向与水平方向的夹角。

(24)

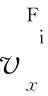
2.2.2 相间车道后车可行性检验

当相间车道后车往本车目标车道变道时，跟相间车道前车一样，为了使本车换道安全，在tC3～T，只需使本车的最后点在相间车道后车最前点之前，即

DRi(0)≥lRi，

(25)

式中：DRi(0)为换道前本车与相间车道后车的初始纵向距离，lRi为(tC3,T)时间段内相间车道前车与本车之间最大相对纵向位移。

DRi(0)=xS(0)-xRi(0)-LT6；

式中：xRi(0)为换道前相间车道后车纵向位置，wRi为相间车道后车宽度，θ3为相间车道后车换道过程车头方向与水平方向的夹角。

(26)

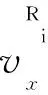
综上所述，当车辆处于边缘车道时，可以根据图8的逻辑判断流程图检验车辆换道可行性。边缘车道的车辆在满足中间车道换道可行性条件的基础上，还需满足相间车道前后车辆可行性检验才能换道。

图8 边缘车道换道可行性检验流程图Fig. 8 Flow chart of lane-changing feasibility test in the edge lane

3 轨迹规划与轨迹跟踪

3.1 轨迹规划

设换道过程中纵向速度不变，横向轨迹为五次多项式，即：

(27)

3.2 基于MPC的轨迹跟踪控制

将车辆简化为三自由度模型(如图9)。根据力学平衡关系，建立如下动力学模型。

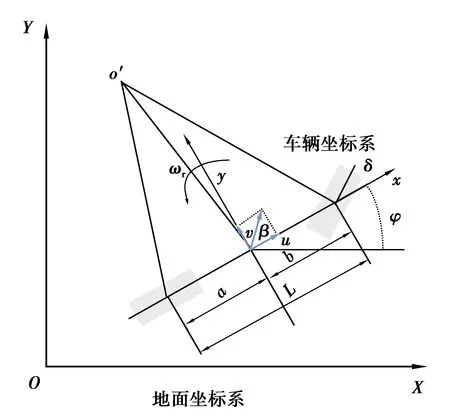
图9 三自由度动力学模型Fig. 9 Three degrees of freedom dynamics model

(28)

(29)

整理可以得到以下微分方程：

(30)

(31)

设车辆坐标与全局坐标的夹角为φ，则全局坐标下的速度和局部坐标下的速度转换关系如下：

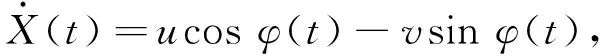
(32)

(33)

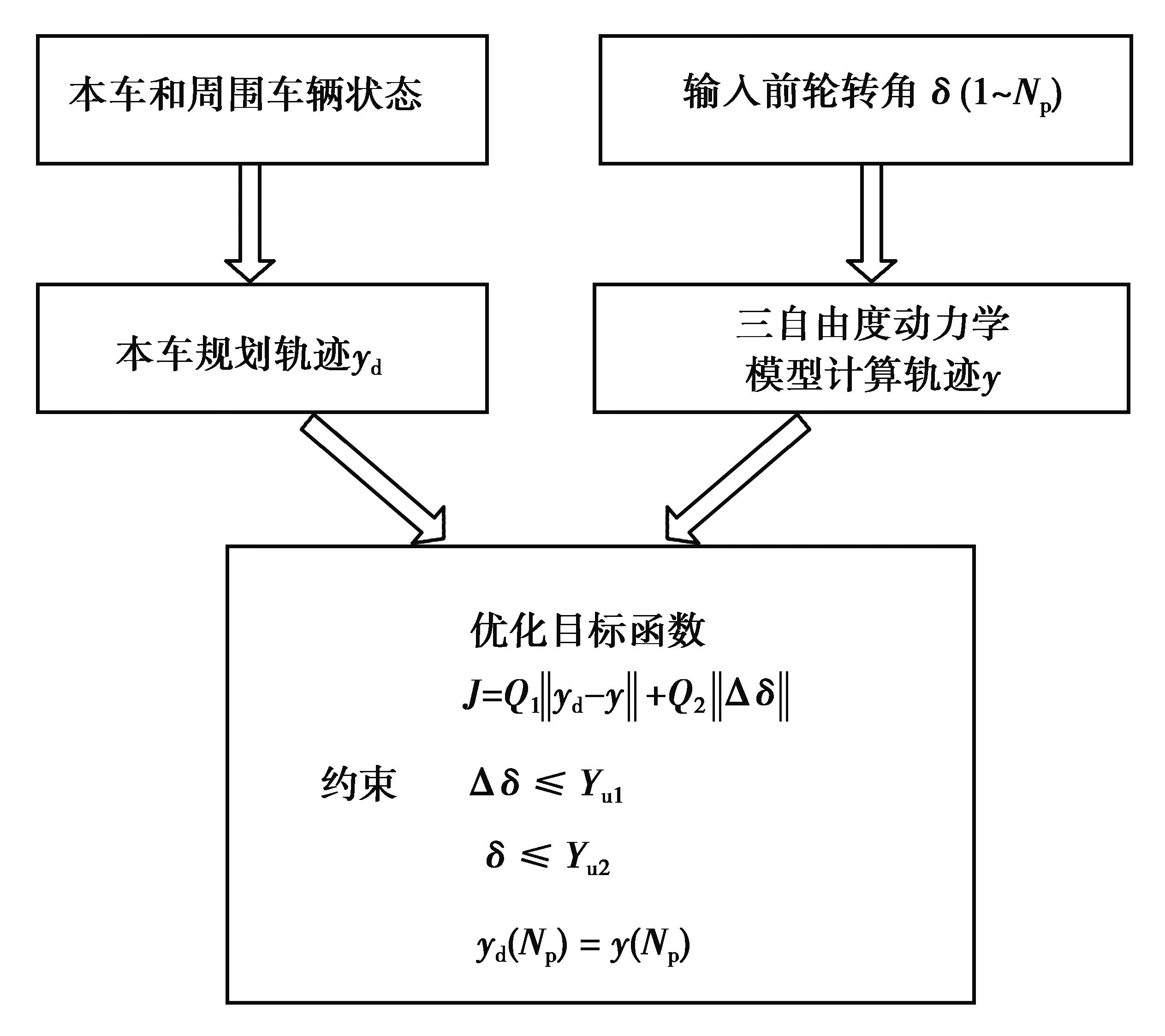
图10 MPC控制方法Fig. 10 Control method of MPC

4 仿真验证和结果分析

4.1 仿真工况

仿真工况1(如图2)，本车处于中间车道，除本车外其他车辆处于车道保持状态，所有车辆纵向初速度和初始位置如表1所示，且假设所有车辆纵向匀速，本车按五次多项式规划的轨迹向目标车道换道。

表1 仿真工况1

仿真工况2(如图11)，本车处于中间车道，1.50 s时刻本车道前车打左转向灯，即往左侧车道变道，其他车辆处于车道保持状态。所有车辆的纵向速度和初始位置如表2所示。

图11 仿真工况2Fig. 11 Simulation condition 2

表2 仿真工况2

仿真工况3(如图12)，本车处于最右侧车道，2.00 s时刻相间车道后车打右转向灯，即往中间车道变道，其他车辆处于车道保持状态。所有车辆的纵向速度和初始位置如表3所示。

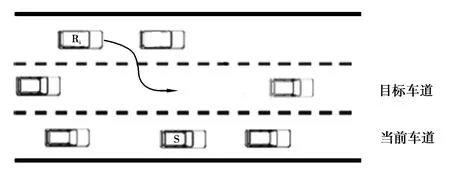
图12 仿真工况3Fig. 12 Simulation condition 3

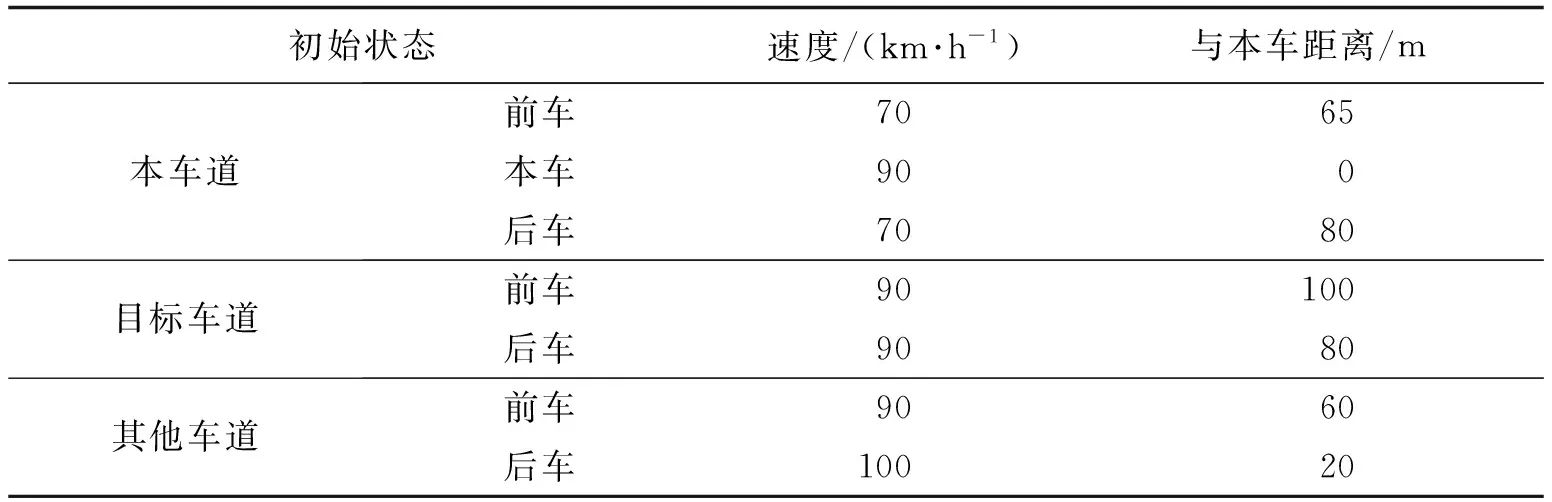
表3 仿真工况3

仿真工况4，本车处于中间车道， 1.40 s时本车道后车打左转向灯，即往左侧车道变道。1.50 s时本车道前车打右转向灯，即往右侧车道变道，其他车辆处于车道保持状态。所有车辆的纵向速度和初始位置如表4所示。

表4 仿真工况4

4.2 换道可行性检验仿真结果

对于仿真工况1，周围车辆均处于车道保持状态，使用改善型换道可行性检验模型和对比模型均能在安全的情况下正常换道。

对于仿真工况2，1.50 s时本车道前车向本车目标车道换道，在1.91s时，本车驾驶员不满意度达到不满意度阈值。在1.91 s时，本车距本车道前后车、目标车道前后车的距离满足对比模型的换道可行性检验条件，因此在1.91 s时向目标车道换道,其换道过程的横向位置和纵向位置如图13和图14所示。在5.91 s时本车换道完成，但本车距离前车的距离比换道前更小(如图13)，驾驶员不满意度仍高于驾驶员不满意度阈值，本车仍然想请求换道，很可能再往原车道换道，因此之前的换道为无效的换道，没有降低驾驶员不满意度。对于改善型换道可行性检验模型，在1.91 s时本车发现前车正在往本车目标车道换道，因此本车继续处于车道保持状态，等待前车换道完成后再决定是否换道，杜绝了向目标车道换道完成后马上又向本车道换道的无效换道过程。因此相对于对比模型，使用改善型换道可行性检验模型更加高效。

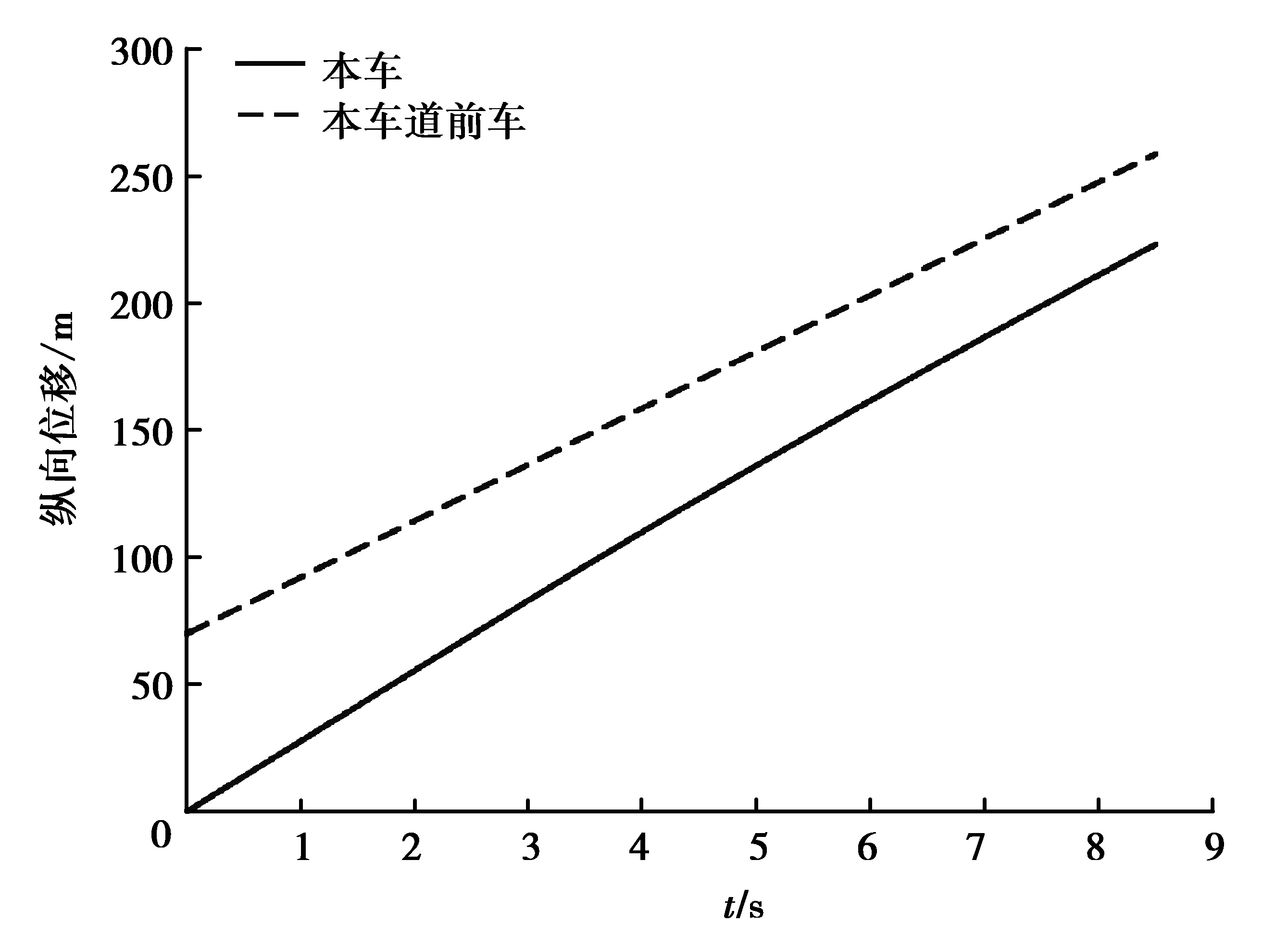
图13 对比模型仿真工况2纵向位移Fig. 13 Longitudinal displacement of the reference model in simulation condition 2

图14 对比模型仿真工况2横向位移Fig. 14 Lateral displacement of the reference model in simulation condition 2

对于仿真工况3，2.00 s时相间车道后车向本车目标车道换道，在2.55 s时，本车驾驶员不满意度达到不满意度阈值。在2.55 s时，本车距本车道前后车、目标车道前后车的距离满足对比模型的换道可行性检验条件，因此在2.55 s时向目标车道换道。对比模型的仿真结果如图15和16，在5.62 s时，本车和相间车道后车纵向位置相同、横向位置很近，所以在5.62 s时两车已经发生碰撞。对于改善型换道可行性检验模型，增加了相间车道车辆的检验，在2.55 s时刻，相间车道后车距本车距离小于最小安全距离，因此不进行换道，从而避免了本车与相间车道后车的碰撞。

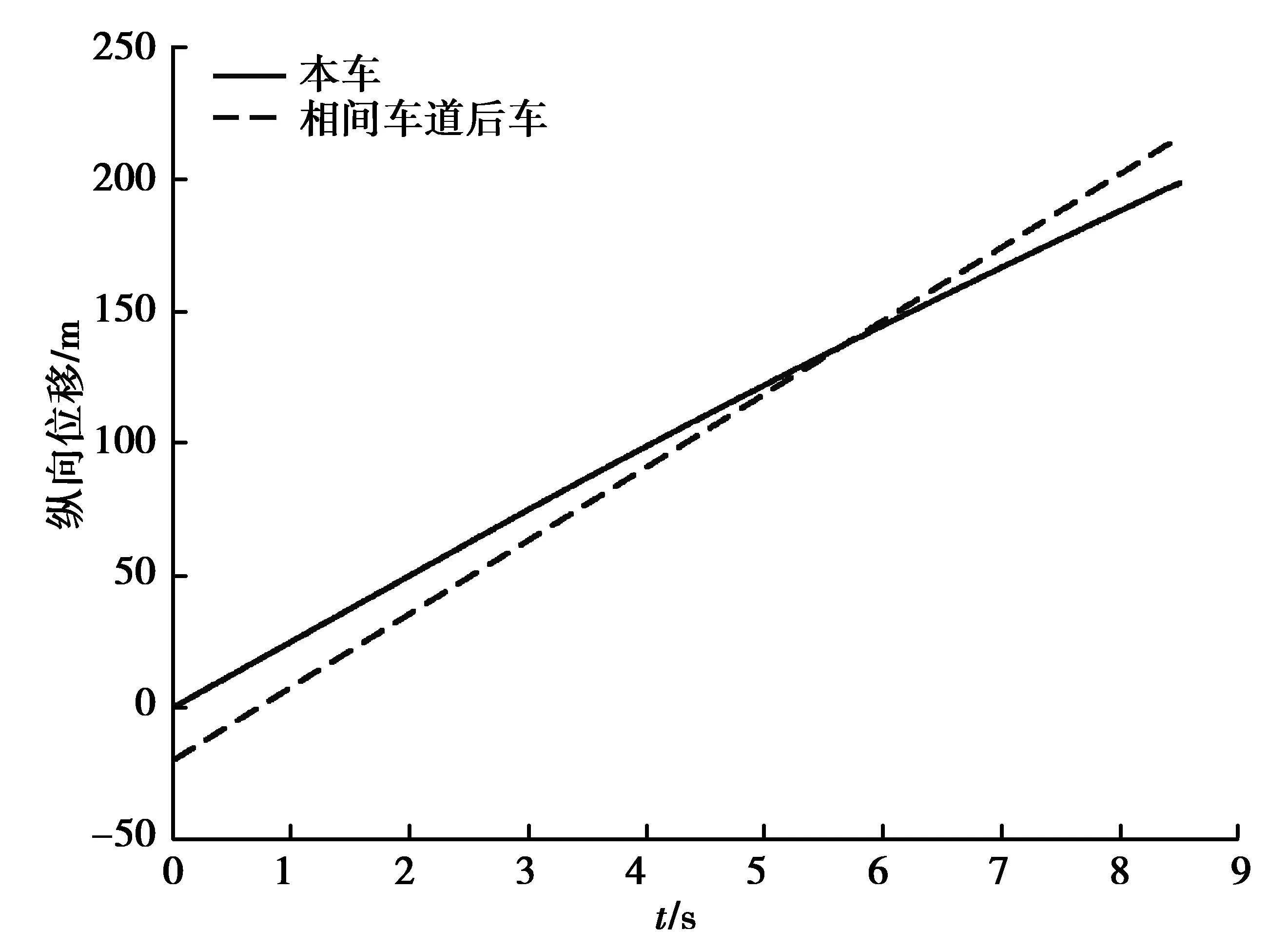
图15 对比模型仿真工况3纵向位移Fig. 15 Longitudinal displacement of the reference model in simulation condition 3

图16 对比模型仿真工况3横向位移Fig. 16 Lateral displacement of the reference model in simulation condition 3

对于仿真工况4，在1.62 s时本车驾驶员不满意度达到不满意度阈值，此时本车与周围车辆的距离和可行性检验阈值如表5所示。由表可知，对比模型的可行性检验结果为通过，而本车距本车道后车的距离不能通过改善型换道可行性检验模型的检验。对比模型的仿真结果如图17～18所示，在4.32 s时，本车和本车道后车纵向位置相同、横向位置相近，所以在4.32 s时两车已经发生碰撞。而对于改善型换道可行性检验模型，在1.62 s时其通不过可行性检验，本车不进行换道，从而避免了本车与本车道后车发生碰撞。因此相对于对比模型，使用改善型换道可行性检验模型更加安全。

表5 本车与周围车辆的距离和可行性检验阈值

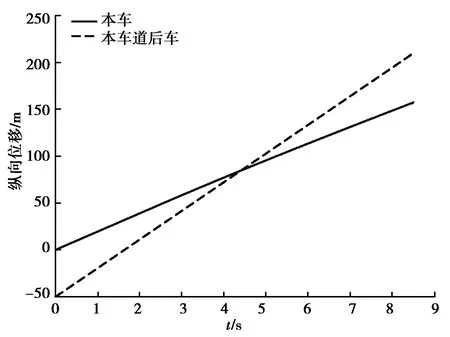
图17 对比模型仿真工况4纵向位移Fig. 17 Longitudinal displacement of the reference model in simulation condition 4

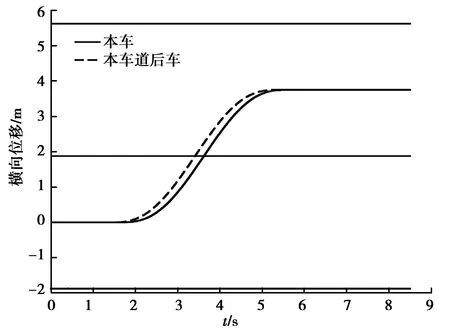
图18 对比模型仿真工况4横向位移Fig. 18 Lateral displacement of the reference model in simulation condition 4

仿真工况2～4中改善型换道可行性检验模型对不同状态的周围车辆和相间车道的换道车辆进行了可行性检验，结果表明该模型比对比模型更加安全高效。

4.3 轨迹跟踪仿真结果

对仿真工况1中的换道轨迹，换道车速为100 km/h，规划横向轨迹如图19所示。MPC控制器的轨迹跟踪结果如图20～21所示。图20中可以看出前轮转角无毛刺，即驾驶过程中方向盘平滑过渡，转向系统能按照输入的方向盘转角响应，最大前轮转角不超过8°，具有很好的驾乘舒适性。由图21可知，最大横向跟踪误差不超过1 cm，具有非常高的跟踪精度。

图19 横向轨迹规划Fig. 19 The lateral trajectory planning

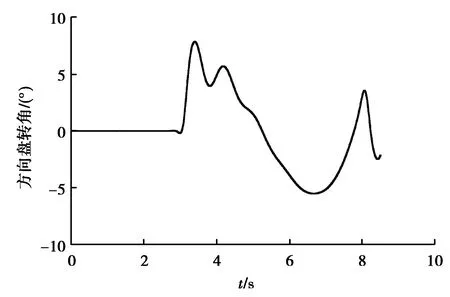
图20 MPC跟踪方向盘转角Fig. 20 The steering angle of the MPC control method

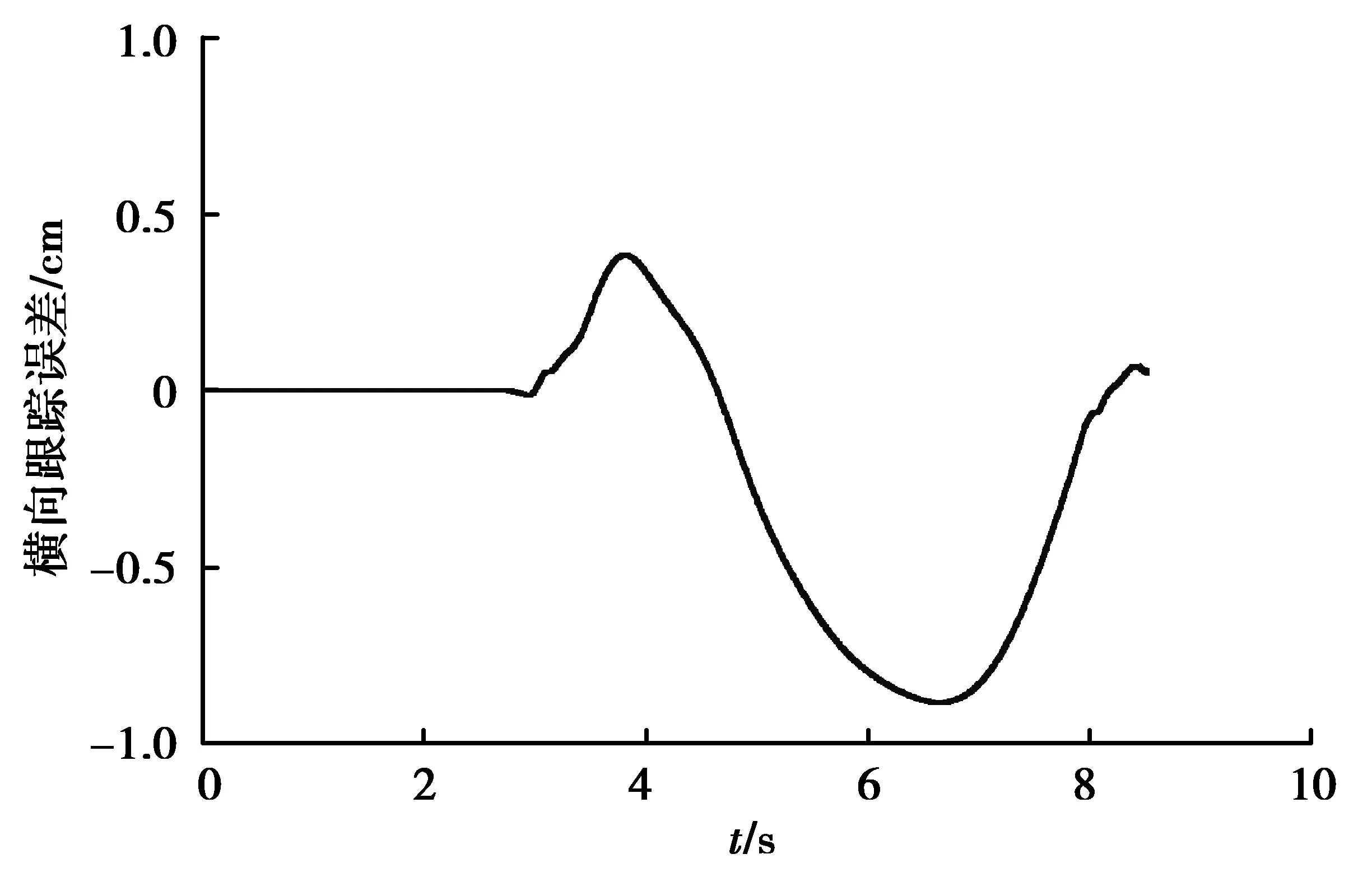
图21 MPC跟踪横向误差Fig. 21 The lateral tracking error of the MPC control method

5 结 论

为实现安全自主换道，建立了车道变换逻辑框架，提出了改善型换道可行性检验模型和基于MPC的轨迹跟踪方法，最后设计了仿真对比试验对所研究的模型和方法进行验证。该研究得到以下结论：

1)提出了中间车道车辆换道可行性检验模型。分析了本车道和相邻车道处于不同状态(车道保持和车道变换)的前后车辆对本车换道的影响，提出了其不影响本车换道的检验要求，确保车辆在不同的驾驶环境下均能安全换道。

2)提出了边缘车道车辆换道可行性检验模型。分析了相间车道处于车道变换的前后车辆对本车换道的影响，提出了其不影响本车换道的检验要求，确保换道过程中本车不与相间车道换道车辆发生碰撞。

3)建立了车道变换逻辑框架，在该框架下融合改善型换道可行性检验模型，使用MPC方法对换道轨迹进行跟踪，然后根据该框架使用Simulink和PreScan建立自主换道模型。仿真结果表明，提出的自主换道模型在安全高效换道的前提下能够对换道轨迹进行精准跟踪。

目前只使用仿真方法对所研究的模型和方法进行了验证，未来需要设计实车实验对所提出的模型进行验证，最终将其用于实际工程中。