基于损伤因子的T形梁桥横向连接构件损伤识别
王立宪, 赵俊豪, 狄生奎, 项长生, 党 聪
(1. 兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2. 浙江中南幕墙科技股份有限公司, 浙江 杭州 310051)
随着我国桥梁建设体量不断增加,桥梁病害问题日益严重.在装配式T形梁桥中,铰缝和横隔板是装配式T形梁共同工作的重要横向连接构件,对其研究至关重要.李国豪等[1]提出了荷载横向分布计算原理,并给出横向连接构件模型,但仅考虑了横向连接构件的剪力.李宏江等[2]通过总结装配式空心板梁铰缝和T形梁横隔板的发展过程,指出横向连接构件的损伤是装配式桥梁承载能力不足的主要原因之一.宋宇峰等[3]基于对国内铰接板设计方法的研究,认为将横向连接构件看作只传递剪力的构件与其实际受力方式存在很大区别,还应考虑传递横向正应力.刘晓春等[4]基于铰缝处的相对位移引入铰缝损伤度,通过静载实验证明了铰缝损伤模型的可靠性.高衡等[5]在装配式T形梁桥与小箱梁结构设计中,将横隔梁的面积均摊到桥面板内.周正茂等[6]为对横向连接构件损伤程度定量描述,提出了考虑铰缝刚度的横向连接构件损伤评价模型,并通过静载试验得出横向连接构件刚度比是识别损伤的有效指标.成琛等[7]将无横隔梁的小跨径钢筋混凝土T形梁视为横向铰接结构,通过遗传算法和损伤铰的横向荷载分布模型进行损伤识别分析.苏明文等[8]利用Midas/Civil建立简支T形梁桥,计算汽车荷载作用下的主梁横向分布系数,通过与传统计算主梁横向分布系数方法对比,验证了二者的计算吻合度.目前横向连接构件损伤识别大多假设横向构件为刚性,以空心板梁铰缝为研究的居多,而以装配式T形梁桥横隔梁和铰缝组合体系的横向连接构件为主要对象的研究相对较少.
本文以装配式T形梁桥为研究对象,考虑装配式T形梁桥的翼缘板变形、横向连接构件的剪力和横向力.将横隔梁截面抗弯惯性矩平均分布于横隔梁的中距作为设想的等刚度桥面板的抗弯惯性矩,提出利用弹簧模拟横向连接构件受力变形的模型,以荷载横向分布计算原理为基础,推导出装配式T形梁桥横向连接构件损伤因子D的计算方法.通过ANSYS模拟、MATLAB理论计算和实验的结果对比,验证计算方法的有效性,更好的对装配式T形梁桥横向连接构件进行损伤识别.
1 横向连接构件损伤计算模型
实际工程中有众多不利因素导致横向连接构件产生损伤,使得相邻两个T形梁间产生竖向相对位移Δ.本文考虑相对位移Δ由横向连接构件竖向剪力g、横向力n、荷载p等共同作用产生,如图1所示.

图1 T形梁受力图Fig.1 T-beam force diagram
对T形梁受力分析,提出采用弹簧a、b的弹簧力Fa、Fb模拟横向力na、nb,铰接杆提供抗剪刚度G,铰接杆剪切变形模拟相邻T形梁间的相对位移Δ,如图2所示.

图2 横向连接构件模型变形图Fig.2 Deformation diagram of transverse connection member model
将横向连接构件模型应用于横向T形梁,如图3所示.图中T形梁编号从左到右依次为T1到Tn,横向连接构件编号从左到右为J1到Jn-1.

图3 装配式T形梁计算示意图
2 横向连接构件损伤因子D计算理论
2.1 基本假定
基于装配式T形梁桥横向计算理论,考虑横向连接构件传递竖向剪力、横向应力,以及横向连接构件的混凝土变形等因素,做以下假定:
1) T形梁上荷载、横向连接构件剪力、横向连接构件混凝土横向力、T形梁相对位移等沿跨径半波正弦分布;
2) 考虑横向连接构件传递的竖向剪力和横向应力,不考虑可能传递的纵向剪力等其他作用;
3) 不考虑材料泊松比ν的影响;
4) T形梁的横隔梁化成等刚度桥面板;
5) 考虑翼缘板的变形.
2.2 考虑相对位移的正则方程建立
根据T形梁桥横向荷载分布理论,横隔梁化成等刚度桥面板的抗弯惯性矩Ir通过下式计算.
Ir=I+Im/lm
(1)
式中:Im为横隔梁抗弯惯性矩;I为主梁的抗扭惯性矩;lm为横隔梁的间距.
等效后的桥面板增加的高度由下式计算:
(2)
由材料力学可知,在横向连接构件宽度一半c内剪切作用产生梁的挠度wt为
(3)
式中:G为横向连接构件混凝的抗剪刚度;h为横向连接构件计算高度;κ为截面剪切系数,矩形截面κ=3/2.
实际工程受各种不利因素影响,抗剪刚度G随时间推移而发生退化.若剪切刚度退化程度为D,则Ji处损伤后的抗剪刚度为(1-Di)Gi.根据式(3)可得Ti与Ti+1的相对位移Δi的近似计算式:
(4)
将相对位移Δi作为Ti与Ti+1的变形协调条件,写出Ji处力法正则方程:
(5)

2.3 计算
当剪力g作用在Ji处,会引起Ji、Ji-1、Ji+1发生变形,单位剪力引起的竖向挠度wg、扭转变形转角θg和悬臂板挠度fg根据下式得出:
(6)
式中:ω和φ分别为单位正弦偏心荷载产生的梁跨中中央挠度和扭转角;l、E、G、Ir、b分别为梁的跨径、弹性模量、抗弯刚度、抗扭惯矩、翼缘板宽度.

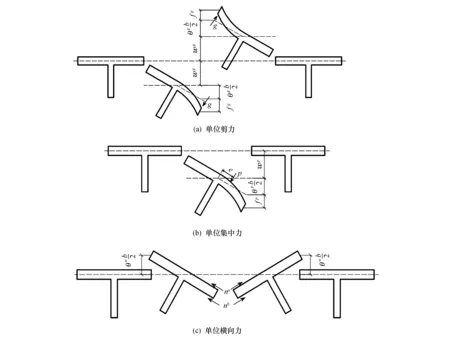
图4 装配式T形梁的变位特征Fig.4 Displacement characteristics of prefabricated T-beam
(7)
当荷载P作用在Ti处,会引起Ji—1、Ji发生变形,单位集中力所引起的竖向挠度wp、扭转变形转角θp和悬臂板挠度fp根据下式得出.
(8)
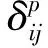
(9)
当横向力n作用在Ji处,会引起Ji、Ji—1、Ji+1发生变形,横向力na=1,nb=-1时,只引起扭转变形,扭转变形转角θn根据下式得出.
(10)

(11)
2.4 计算剪力峰值gj
在装配式T形梁上加载一组纵向分布的正弦荷载pj,通过下式可以得到各T形梁分布的荷载Qj:
(12)
式中:∂j为Ti中心的竖向位移.
由各个T形梁在竖向力的平衡条件可以求得gj:
(13)
2.5 计算横向力nj
利用弹簧力Fa、Fb模拟横向力na、nb,通过胡克定理可知:
(14)

在Ji处的相对转角ψi可由下式求得
(15)
将相对转角ψi作为Ti与Ti+1的变形协调条件,写出Ji处的力法正则方程:
(16)

(17)
(18)
(19)
将式(13)、(17)~(19)带入式(16),再给定pj得到nj.
2.6 计算横向连接构件损伤因子Di
为方便计算,引入扭转位移与主梁挠度之比公式和悬臂板挠度与主梁挠度之比为
γ=(φb/2)/ω
(20)
β=f/ω
(21)
(22)
建立损伤因子Di与T形梁位移之间的方程:
(23)
Di=1-1/μi
(24)
式中:μi为横向链接构件柔度,μi越大,横向链接构件刚度越小.
3 数值分析
3.1 模型建立
以单跨简支T形梁为研究对象,桥梁跨径16 m,梁高1.1 m,翼缘板宽1.6 m,翼缘板厚0.16 m,梁肋宽0.18 m,横隔梁化成等刚度桥面板增加的高度为0.41 m,横向由10片T形梁通过宽度为2 cm横向连接构件的混凝土连接,T形梁和横向连接构件的混凝土强度等级为C40.T形梁编号自左至右为1号至10号,横向连接构件的编号自左至右为1#至9#,如图5所示.

图5 装配式T形梁桥横向布置与构件尺寸(cm)
根据结构尺寸与图3装配式T形梁横向链接构件计算模型,利用ANSYS建立装配式T形梁有限元模型,如图6所示.本模型由T形梁单元(T-beam element,TBE)和横向连接单元(transverse connection element,TCE)组成,TBE用实体单元SOLID65模拟,TCE用弹簧单元COMBIN14模拟.其中TCE中有两种COMBIN14单元设置,一种只模拟轴向力为横向连接弹簧单元(transverse connection spring element,TCSE),建立在悬臂板高的1/4和3/4处;另一种只模拟竖向剪力称为横向连接连杆单元(transverse connection link element,TCLE),建立在悬臂板高的1/2处,模型如图6所示,两种COMBIN14单元的弹簧刚度根据下式可得:

图6 ANSYS模型Fig.6 ANSYS model
(25)
式中:Ec为横向连接构件混凝土弹性模量;Gc为横向连接构件混凝土剪切模量;h为横向连接构件计算深度;c为横向连接构件计算宽度的1/2;le为TCE间距,本模型中le=20 cm.
3.2 损伤工况
为简化计算,将作用在跨中xi=L/2的集中荷载Pi=100 kN根据下式
(26)
转化为峰值为pi=12.5 kN/m的半波正线荷载,如图7所示.各工况见表1设置.

表1 工况设置

图7 集中荷载转化图Fig.7 Conversion diagram of concentrated load
损伤程度通过模型弹簧刚度的折减实现,工况1和工况2为无损伤但荷载作用在不同位置,工况3至工况5为损伤位置和损伤程度相同但荷载作用位置不同,工况3和工况7为荷载作用位置和损伤位置相同但损伤程度不同,工况5和工况6为荷载作用位置和损伤程度相同但损伤位置不同.
3.3 数值模拟与理论计算结果对比
上述7种工况利用ANSYS数值模拟和MATLAB理论计算,分别得到横向连接构件剪力、横向连接构件横向力、相邻T形梁翼缘板的相对竖向位移和损伤因子D的结果,通过对比分析验证计算方法的有效性,分析结果如图8所示.

图8 分析结果对比
理论计算和数值模拟的横向连接构件剪力结果最为接近,最大误差出现在工况3的3#横向连接构件处,如图8a所示,误差为0.476 kN/m.
横向连接构件横向力的理论计算和数值模拟结果的吻合程度较高,最大误差出现在工况5的6#横向连接构件处,如图8b所示,误差为3.794 kN/m.
相邻T形梁横向连接构件处的相对位移结果表明,理论计算和数值模拟的最大误差出现在工况6的6#横向连接构件处,如图8c所示,误差为1.26×10-5mm.
横向连接构件剪力与横向连接构件处相邻T形梁翼缘板相对位移的分布规律大体一致,但在损伤位置处有较大差别,这里列出工况4的计算结果,如图9所示.
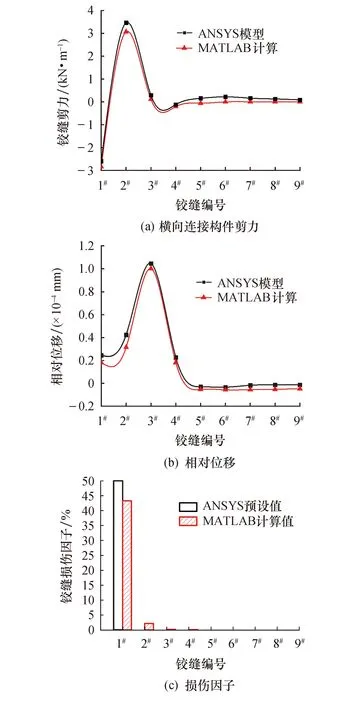
图9 工况4结果对比Fig.9 Operating condition 4 comparison of results
通过图10可知,本文提出的横向连接构件损伤识别方法可以较好的定位损伤位置和识别损伤程度,且荷载作用位置与横向连接构件损伤位置的距离对理论计算的损伤因子D有所影响.工况3至工况5的ANSYS预设损伤因子是50%,工况3理论计算的D是47.18%,而工况4理论计算的D为43.26%,工况5理论计算的D仅为25.81%,误差分别为2.82%、6.74%和24.19%,如图11所示.

图10 损伤因子D计算结果对比Fig.10 Comparison of damage factor calculation results

图11 加载位置对横向连接构件损伤因子D计算的影响
由图11可知,在损伤位置和损伤程度相同的情况下,荷载作用离损伤横向连接构件处越近,损伤因子计算值D越接近预设值,即损伤识别精度越高.
通过对上述7种不同工况的理论计算结果和数值模拟结果对比,得出本文提出的T形梁桥横向连接构件损伤计算理论的有效性.
4 实验验证
为进一步验证装配式T形梁桥计算理论的横向连接损伤识别效果.以一座实体装配式T形梁桥为研究对象,该装配式T形梁桥如图12所示,桥梁共有一跨,跨径为13 m,东西走向,由11个T形梁和10个横向连接组成,每个T形梁宽1.6 m,梁高1 m,横隔梁高0.7 m,梁肋宽0.18 m.桥面铺装采用沥青混凝土整体现浇.T形梁编号由北向南依次编号为1号,2号,…,11号,横向连接由北向南依次编号为1#,2#,…,10#.通过桥梁静载试验,得到桥梁跨中位置T形梁中心竖向挠度,通过装配式T形梁桥的横向连接损伤理论,实现对装配式T形梁桥横向连接整体性能评估.本试验选择能够反应桥梁结构的最不受力状态及最不受力截面进行加载,即桥梁跨中截面作为测试截面加载,现场如图13所示.测试截面共设置11个竖向挠度测点,每个测点设置在T形梁梁肋底中心线位置,位移挠度测点布置图,如图14所示,加载车辆的轴距与轴重如表2所列.

表2 加载车辆的轴距与轴重

图12 桥梁实景Fig.12 Bridge scene

图13 现场实验

图14 位移挠度测点布置图Fig.14 Layout of displacement and deflection measuring points
按照加载车辆的位置,共分为三种工况如表3所列.采用Midas/Civil程序进行结构无损状态分析,并以工况一试验结果进行对比.

表3 加载工况
由图15和图16可知,试验中第3号T形梁和第7号T形梁的竖向位移与数值计算结果相差较大,横向连接损伤因子D的计算结果指出2#、6#和7#横向连接发生损伤.

图15 工况1的T形梁竖向挠度值

图16 工况1的横向连接损伤因子DFig.16 Vertical deflection of T-beam in case 1
5 结论
1) 根据T形梁桥横向荷载计算理论,考虑横向连接构件剪力、横向连接构件横向力和翼缘板变形,将T形梁的横隔梁化成等刚度桥面板,通过折减横向连接构件刚度引入损伤,利用变形协调条件和力法方程,计算出横向连接构件剪力、横向连接构件横向力,得到横向连接构件损伤因子计算式,提出了装配式T形梁桥横向连接构件损伤计算理论.
2)通过7种不同工况对比发现不同的加载位置、损伤位置和损伤程度的不同,理论结果和有限元结果均能较好吻合,通过实桥实验证明本文所提装配式T形梁桥横向连接构件损伤计算理论的有效性,且荷载作用位置越接近横向连接构件损伤位置,损伤识别精度越高.

