基于数字孪生技术的往复式空气压缩机效率预测方法研究

余建平, 胡 爽, 刘兴旺, 田有文, 仇宏伟, AKOTO Emmanuel

(兰州理工大学 石油化工学院, 甘肃 兰州 730050)

往复式空气压缩机在工业系统中有200多年的使用历史.它以适应性强、排气量范围广、高效和高压缩比等不可替代的优势在石油化工、机械和建筑等领域被广泛使用[1-2].

往复式空气压缩机的效率受排气量、排气压力、冷却水量、冷却水温和余隙容积等多种因素影响.若通过工业实验方法寻找最佳参数组合,实现压缩机高效运行,则需要耗费的时间长而且实验成本高.同时,各因素间强耦合、非线性的特性也使得用通过气体热力学、动力学建立起的各变量间理论关联式来预测压缩机效率存在困难[3-6].

若采用机器学习的方法建立往复式空气压缩机输入、输出变量间的数字孪生体模型,并在孪生体模型上进行参数寻优,则有可能弥补实验或理论分析研究方法的不足.王伟等[7]利用BP神经网络(BPNN)对半封闭往复式压缩机进行了性能预测,证明了神经网络作为预测模型的可行性.丁国良等[8]采用人工神经网络与传统理论模型相结合的方法,建立了智能化往复式空气压缩机模型,并利用人工神经网络自学习和泛化功能提升了压缩机的容积效率.刘超[9]将模糊算法用于神经网络,对压缩机性能进行了预测,预测结果与实测结果吻合.已有研究表明,以BP神经网络为基础的数字孪生模型可用来分析预测往复式空气压缩机效率.然而,由于影响压缩机效率的因素众多,各变量相互耦合嵌套,传统BPNN模型的训练工作量大、寻优过程易陷入局部最优解、不易实现全局最优,所以诸多困难限制了BPNN模型在压缩机效率预测中的应用[10].鉴于此,本文提出利用主成分分析法(principal components analysis)[11]精简压缩机效率的关键指标,在传统BPNN模型基础上引入鲸鱼优化算法实现全局参数寻优,最终达到提高计算速度、改进预测精度和实现全局寻优的目的.

1 实验数据采集

实验台以VW-3/7-a水冷、油润滑往复式空气压缩机为基础,根据实验要求生产厂家在压缩机气缸上增设了压力、温度和可调余隙容积等测量接口,安装完检测元器件后用组态软件开发了压缩机操作和实验数据测量系统.实验台结构如图1所示.基本参数包括:公称容积流量为3 m3/min,轴功率为18 kW,额定排气压力为0.7 MPa,可调转速为500～1 450 r/min,外形尺寸为2 580 mm×1 900 mm×1 700 mm,净重为2 065 kg,电动机功率为22 kW,电机型号为Y225M-8三相异步电机.

图1 往复式空气压缩机实验台结构图

2 压缩机效率预测模型的构建方法

CIWOA-BPNN模型训练的步骤包括:

1) 实验数据采集和预处理.采用拉丁超立方抽样法确定数据采集范围,对采集到的360组实验数据(涉及26种影响因素)进行缺失值和异常值分析,保证所得数据均为完整、有效数据.

2) 关键因素分析.应用主成分分析法对影响压缩机效率的主要因素进行分析,寻找关键的指标因素.

3) CIWOA-BPNN模型训练.采用Cubic map混沌映射初始化鲸鱼位置,假定当前最佳候选解是目标猎物或者接近最优解,并且不断地对初始权值和阈值进行寻优,实现全局搜索.

4) 可靠性验证.在360组测试数据中随机选取300组进行模型学习训练,利用剩余的60组数据对模型可靠性进行检验分析.具体流程如图2所示.

图2 CIWOA-BPNN模型训练流程图Fig.2 CIWOA-BPNN model training flow chart

2.1 基于主成分分析的数据处理

压缩机实验测试系统给出了转速、余隙容积(相对)、压缩机排量、冷却水流量、一级环境温度、一级吸气压力、一级排气温度、一级排气压力、二级吸气压力、二级排气压力、二级排气温度、储罐压力、储罐温度、冷却水进口温度、冷却水出口温度、环境湿度、喷嘴温度、油泵压力、电流、电压、喷嘴压力、机器功率、稳态下一级压缩功、稳态下二级压缩功、扭矩和大气温度等26种影响因素的测量数据.由于实验台测量数据齐全,所以通过这些数据可计算出压缩机的理论指示效率、轴效率和内效率等多种效率.为了反映压缩机整体能量的转换情况,本文采用GB 19153—2019标准[12]中规定的空气压缩机输功效率作为评价指标,其物理意义为空气压缩机输出压缩空气中所具备有效能与其生产压缩空气所消耗电能的比值,即

(1)

式中:ηwC为空气压缩机输功效率;p1为机组吸气压力(绝压),MPa;p2为机组排气压力(表压),MPa;ev为机组比功率,kW/(m3·min-1),即

(2)

式中:Pcorr为按GB/T3853测量、修正计算的机组功率,kW;qv,corr为按GB/T3853测量、修正计算的机组容积流量,m3/min;K14为机组比功率吸气温度修正系数,即

(3)

式中:Tx为空气压缩机实测吸气温度,K .

将26种因素直接用于孪生模型的训练会导致计算时间过长且不易收敛.因此,采用主成分分析法对问题进行简化,找出影响压缩机效率的关键指标.对实验数据进行标准化处理后进行主成分分析,得到各因素总方差示意图,如图3所示.分析26种变量特征值的方差百分比可以看出,转速、余隙容积、压缩机排量和冷却水流量共占总方差百分比(贡献率)的83.467%.因此,选择转速、余隙容积、压缩机排量和冷却水流量作为影响效率的主要变量.

图3 总方差图Fig.3 Total variance figure

2.2 CIWOA-BPNN预测模型的建立

虽然BP神经网络成熟并被广泛使用,但是存在反向搜索效率不高、不易收敛等问题.本文将改进后的鲸鱼优化算法CIWOA应用于神经网络反向寻优过程,通过优化种群变量的选取、调整适应度函数等措施实现快速、准确地训练神经网络模型.CIWOA-BPNN模型的寻优流程如图4所示.

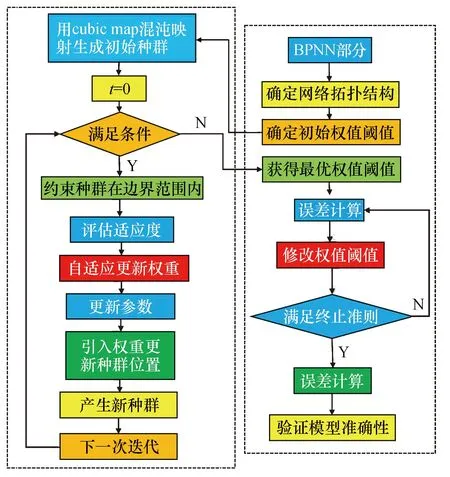
图4 CIWOA优化BP神经网络流程图Fig.4 Flow chart of CIWOA optimized BP neural network

采用Cubic map混沌映射初始化鲸鱼位置[13],设置初始参数.Cubic map混沌映射表达式为

(4)

式中:ρ为控制参数;xk为第k个混沌数.

对各代的每个鲸鱼个体按照其规则进行位置更新时,本文采用自适应权重的方法[14].自适应权重w的表达式为

(5)

式中:wmax、wmin分别为自适应权重的起始值和最终值;m为[0,1]中的随机数;t为当前迭代的次数;maxgen为最大代数.

由于在最初设计时搜索速度的位置是随机的,所以改进后的鲸鱼算法假设当前最佳候选解是目标猎物或者接近最优解.在确定了最佳搜索代理之后,其他搜索代理都会尝试向最佳搜索代理靠近,并更新它们的位置.表达式为

式中:D为个体与目标之间的距离;t为目前迭代次数;A和C为系数向量;X*(t)为第t次迭代中猎物的位置;X(t)为每次迭代更新的位置;w为自适应权重;a为收敛因子,在整个迭代过程中a由2线性降至0;r1和r2为随机向量,其模的取值范围为[0,1];I为方向与r1相同的单位向量.

2.3 模型的参数设置

CIWOA-BPNN模型采用3层网络结构,输入数据包含转速、余隙容积、压缩机排量和冷却水流量,输出数据为压缩机效率.隐含层神经元节点数根据经验公式计算选取[15],即

(10)

式中:b为1～10的常数;l为BPNN隐含层节点数;m为输入层节点数;n为输出层节点数.

按经验公式计算出隐含层节点数的取值范围后,逐个代入神经网络进行训练测试.CIWOA优化算法的初始参数设置为种群规模数30、最大进化代数50、自变量上限3、自变量下限-3. BPNN模型训练次数为1 000,训练目标为0.01,学习速率为0.1.

2.4 预测模型评价指标

为验证BPNN、CIWOA-BPNN模型的实际应用效果,选用决定系数(R)、相对误差(RE)、均方误差(MSE)作为评价模型的预测指标.其中,R最大值为1,最小值为0,R越接近1拟合效果越好,表达式为[16]

(11)

RE、MSE数值越小越好,为0时说明预测值与真实值相等,表达式分别为

3 预测模型可靠性检验

3.1 模型预测结果对比分析

模型训练后测试结果与实际结果的对比分析如图5和图6所示.图中,效率为空气压缩机输功效率.

图5 BPNN模型预测结果图Fig.5 The prediction result of the BPNN model

图6 CIWOA-BPNN模型预测结果图Fig.6 The prediction result of the CIWOA-BPNN model

经对比可以看出,改进后CIWOA-BPNN模型中实际值与预测值的拟合效果优于BPNN模型,同时也突显了改进鲸鱼算法的优良特性.

3.2 模型可靠性验证

分别把BPNN和CIWOA-BPNN模型的预测值与实际值进行相关性分析,结果如图7和图8所示.图中,蓝色为直线y=x,红色为预测结果拟合线.

图7 BPNN模型预测结果线性拟合图Fig.7 Linear fitting diagram of the prediction results of the BPNN model

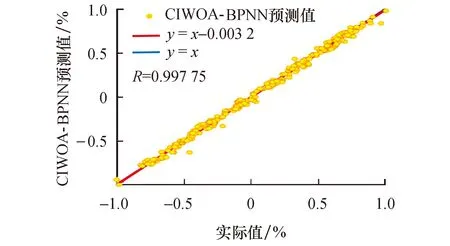
图8 CIWOA-BPNN模型预测结果线性拟合图Fig.8 Linear fitting graph of the CIWOA-BPNN model prediction results

图7中,BPNN 模型拟合方程为y=0.8x+0.17,拟合结果R=0.899 93;图8中,CIWOA-BPNN模型拟合方程为y=x-0.003 2,拟合结果R=0.997 75.可以看出,CIWOA-BPNN模型拟合结果的决定系数R最接近1,拟合效果最优.这是因为改进后的鲸鱼优化算法引入了自适应权重,代数自适应调整权重使得鲸鱼捕食效率逐渐提高,避免陷入局部最优解.同时,还因为改进的鲸鱼优化算法在初始种群时应用了Cubic map混沌映射初始化鲸鱼位置,假设当前的最佳候选解是目标猎物或者接近最优解,增强了全局寻优能力.由此进一步验证了CIWOA-BPNN模型作为预测稳态效率工具的正确性和鲁棒性.

经计算可得BPNN模型稳态效率预测结果包括:REmax为0.089 1,REmin为-0.056 8,对应的MSE为0.002 6;改进后的CIWOA-BPNN模型稳态效率预测结果包括:REmax为0.005 7,REmin为-0.005,对应的MSE为0.000 043.原始BP神经网络的误差分布范围较广泛,且正负值都有.这是因为在开始训练时,初始权值和阈值为随机分布,学习率较大且为恒定值,预测值在真实值左右震荡,并且较难趋近.而改进的鲸鱼算法优化了原始BP神经网络的权值和阈值分布规律,并随着训练的进程自适应减小学习率,使预测值更容易沿固定方向收敛至真实值.

由图9可以看出,CIWOA-BPNN模型的预测值偏离真实值的方向较为统一,大部分相对误差都偏小,说明预测值从负方向不断趋近真实值.因此,改进后的模型预测结果误差均优于改进前的,改进后的模型预测精度得到明显提升.

图9 稳态效率预测结果相对误差折点图Fig.9 Line chart of relative error of steady-state efficiency’s prediction results

4 结论

针对以BP神经网络为基础的往复式空气压缩机数字孪生模型存在训练时间长、工作量大、易陷入局部最优解和不易实现全局最优等问题,本文提出了基于主成分分析并结合鲸鱼优化算法的孪生模型构建方法.通过300组实验数据对模型进行训练和60组实验数据对模型进行检验,得出以下结论:

1) 对影响压缩机效率的26个因素进行主成分分析,转速、余隙容积、压缩机排量和冷却水流量是最主要的影响因素,4个因素的贡献率占总贡献率的83.467%;

2) 改进的鲸鱼优化算法具有较快的计算速度,实现了全局寻优,避免了寻优过程陷入局部最优解;

3) 与传统BPNN模型相比,CIWOA-BPNN模型具有更高的准确度;

4) 实验台为中等规模的工业化测试平台,实验过程与工程实际工况接近,因而可以容易地将基于实验测量建立的孪生模型移植到类似的压缩系统.