考虑附加弯矩后的大直径螺栓承载能力研究

张宏宇，刘晓华，范 刚，王捷冰，李凤全

（1.空间物理重点实验室，北京，100076；2.首都航天机械有限公司，北京，100076）

0 引 言

螺栓连接作为机械、建筑等结构中最常用的连接方式，在工程中起着不可替代的作用。采用工程方法计算螺栓的连接强度时，假设螺栓及连接结构刚度较好，螺栓长度有限，故一般不考虑弯矩效应，往往认为其仅承受拉伸载荷（轴向）和剪切载荷（横向），通过安全系数保证其连接可靠性，未对其承载特性中的弯矩开展深入研究［1-3］。

而相关研究表明，若不满足前提假设要求，工程计算方法存在较大偏差，不能忽略弯矩效应。近年来，国内外学者对此开展了相关研究及试验工作。楼国彪等［4］对于建筑结构中的典型端板连接螺栓开展了详细分析，发现连接端板等相关结构的柔性会导致撬力作用效应，使螺栓承受附加载荷，出现螺栓受弯，而试验表明，高强度螺栓由于撬力作用效应而额外承受的拉力可达10%～50%；暴伟等［5］对铸钢件连接螺栓受拉性能开展了试验和分析，弯曲应力和拉应力比值可达0.6，对螺栓受力不利，设计中应考虑螺栓弯矩影响；董瑾等［6］对火力发电厂汽轮机螺栓由于结构偏差导致的弯曲应力进行了全面的分析，采用平均应力Morrow 修正式对弯曲应力对疲劳特性的曲线的影响进行了研究，得到了不同偏转角下的螺栓低周疲劳特性曲线，偏转角引起的局部附加应力对螺栓强度影响较大，必须采取结构措施降低弯曲应力；文献［7］～文献［11］对端板连接高强螺栓开展了相关分析及试验工作，获得了典型端板连接结构单向载荷状态下螺栓弯矩，结果表明刚度越弱，螺栓弯曲越显著。

大直径螺栓作为一种特定的连接螺栓，广泛应用于导弹分离结构设计中［12］，通常也是按照不考虑弯矩效应开展设计与校核。如徐孝诚［13］对导弹圆截面轴向连接螺栓载荷开展了公式推导，在不考虑螺栓弯矩影响的前提下，提出了普适性公式。

但也有研究成果表明，一些情况下不能忽略弯矩效应的影响。侯传涛等［14］针对某次整流罩倒锥段的联合静力试验中大直径爆炸螺栓在未达到1.5 倍使用载荷作用下出现假品拉断现象开展了分析，得出了附加弯矩会使得大直径螺栓的承载能力降低的结论，初步揭示了大直径螺栓提前破坏的内在机理。杨帆等［15］针对圆形舱段大直径螺栓连接结构，对比了经验公式和有限元分析得出的大直径螺栓载荷，提出了优化后的大直径螺栓载荷计算公式，提出了等效轴力的概念，并建议后续型号应开展有限元分析，考虑附加弯矩作用；但其提出的公式中未考虑材料塑性影响，且未进一步在地面试验中开展验证工作。

本文在此基础上，进一步开展了有限元分析及地面试验验证等工作，获得了大直径螺栓受力过程中的承载特性，提出了大直径螺栓强度评估工程方法。

1 工程方法

根据文献［13］提出的普适性公式开展研究，在截面弯矩作用下，对接面上形成拉伸区和压缩区，拉伸区螺栓承受拉伸载荷，压缩区端框受压，螺栓则有不同程度的卸载，相关示意见图1。

图1 弯矩作用下圆截面连接螺栓受力示意Fig.1 Stress diagram of circular section connecting bolt under the action of bending moment

经过推导，轴弯联合作用下的螺栓载荷计算公式为

式中n为螺栓个数；T为轴力。

某舱体与过渡段通过8 个M24 大直径螺栓连接，位置及编号示意见图2。

将载荷代入式（1），可得大直径螺栓最大轴力为110 kN。

2 数值方法

2.1 试验预示

舱体由蒙皮和盒型件组成，通过8个大直径螺栓与过渡段连接，传力路径复杂。本文采用有限元分析软件开展仿真分析，为了尽可能真实描述舱体受力状态，模拟载荷传递路径，在结构件关系处理上均采用了接触处理方法。

由于载荷和结构具有对称性，取舱体结构的一半并施加对称边界条件进行分析，以减小计算量。大直径螺栓局部连接结构如图3所示。

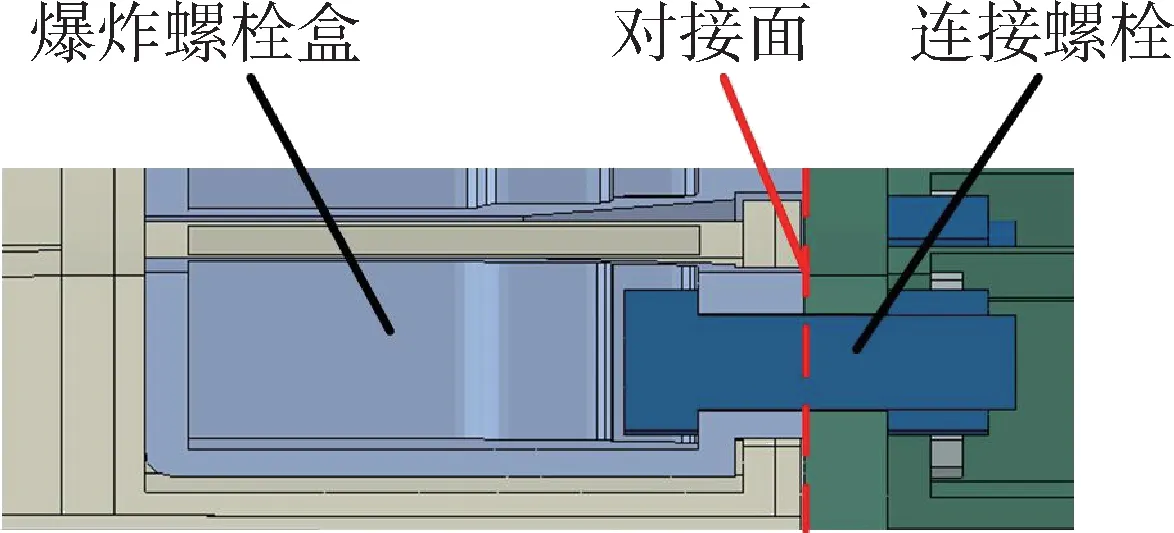
图3 大直径螺栓局部连接结构示意Fig.3 Local deformation of large diameter bolt connection

大直径螺栓载荷提取结果见图4，局部结构变形情况见图5。大直径螺栓最大载荷位于2#（2'#）大直径螺栓，最大轴力93 kN，最大弯矩330 N∙m。由图5可知，载荷传递过程中，局部端框弯曲变形，使得螺栓头和螺母局部与舱体结构接触区域变形不协调，在传递螺栓轴力的同时，对螺栓产生了附加弯矩。

图4 大直径螺栓载荷Fig.4 Finite element analysis results of large diameter bolt load

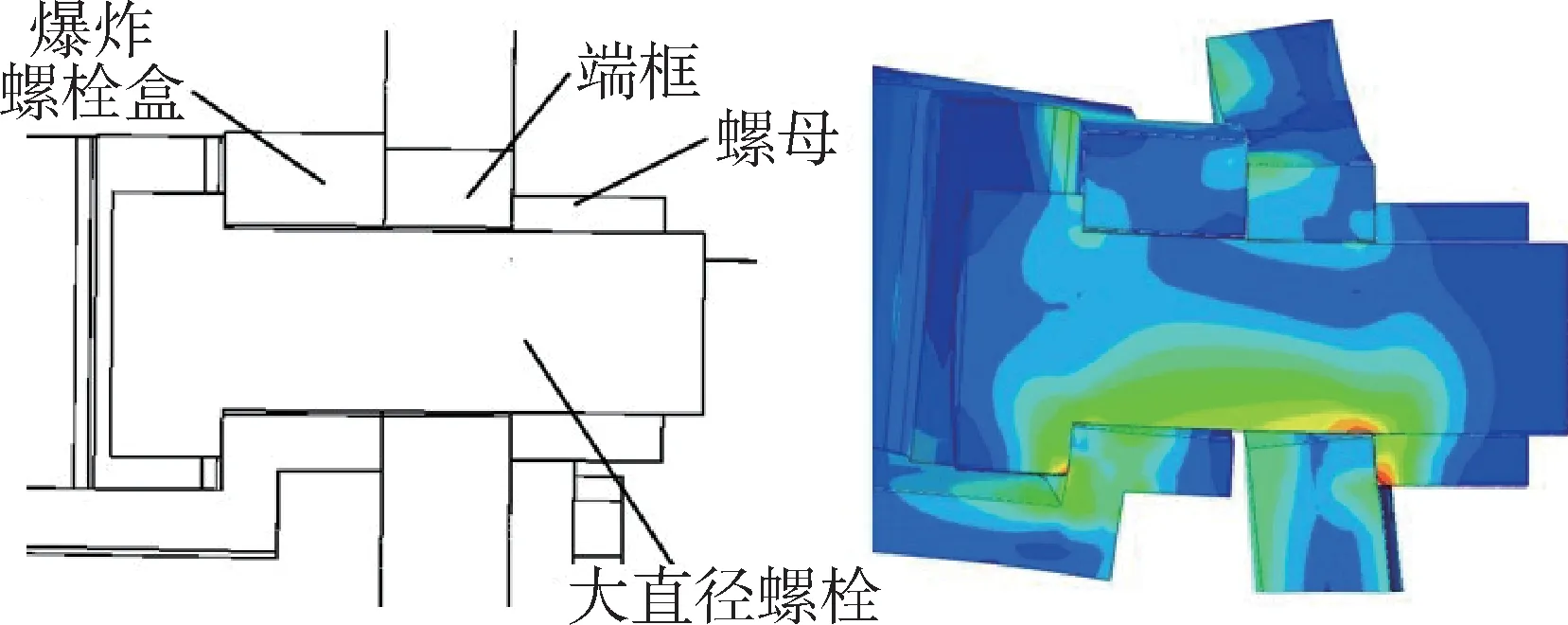
图5 大直径螺栓局部连接结构及变形示意Fig.5 Local deformation of large diameter bolt connection

2.2 降载研究

对于螺栓而言，在结构设计过程中应保证其承受拉伸及剪切载荷，避免承受弯矩，否则将大大削弱螺栓承载能力。由上文分析可知，大直径螺栓附加弯矩是由于传载过程中局部连接结构变形不协调所产生的，因此，如何降低局部变形，进而降低大直径螺栓附加弯矩，提高承载能力，是结构优化的核心所在。

为了提升计算效率，基于简单模型，本文从结构反装、提高刚度、增加球副等方面开展了相关结构优化状态下分析。分析简化模型剖面如图6所示。

图6 大直径螺栓弯矩降载分析简化模型Fig.6 Analysis model of large diameter bolt additional bending moment load reduction

降载方案分别见图7 至图9。反装结构降载方案中，通过大直径螺栓盒结构反装，降低大直径螺栓与结构区域的弯曲变形来降低弯矩；局部加强降载方案中，通过增加盖板提高大直径螺栓盒刚度，以降低大直径螺栓与结构区域的弯曲变形来降低弯矩；关节降载方案中，通过增加球副增加转动自由度释放变形，以降低局部变形不协调情况，从而降低附加弯矩。

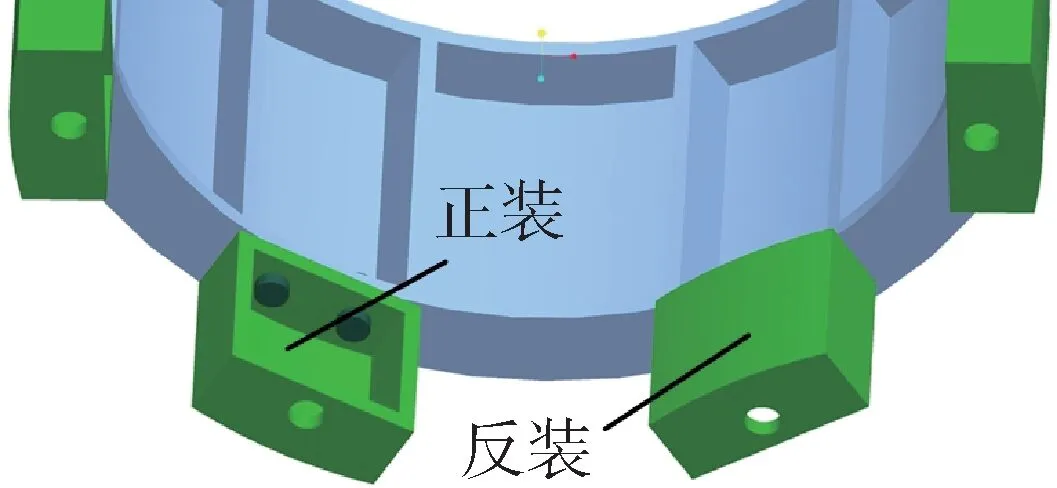
图7 反装结构Fig.7 Reverse installation programme

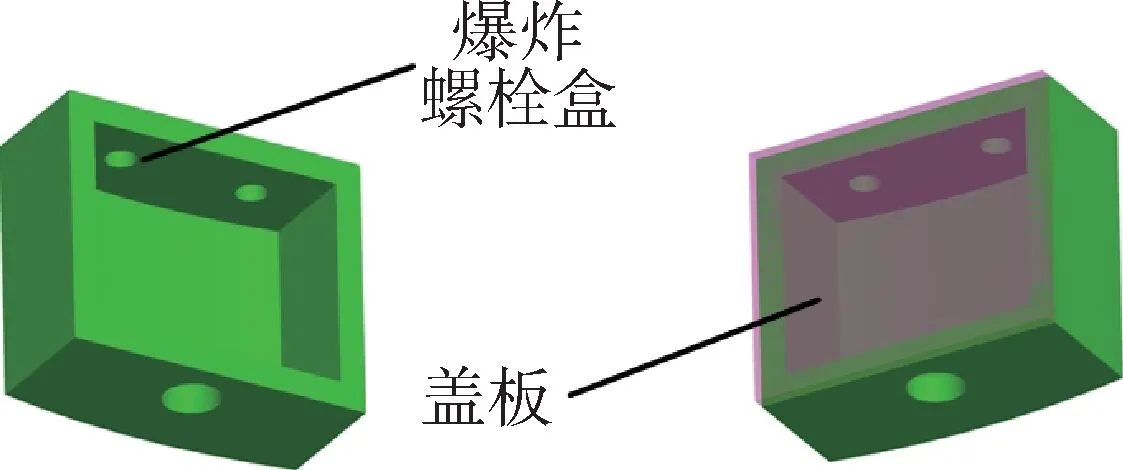
图8 盖板结构Fig.8 Cover-palte programme

图9 大直径螺栓局部连接结构示意Fig.9 Spherical joint programme

4 种状态下大直径螺栓轴力与弯矩见表1。由分析结果对比可知，与基准设计状态相比，3 种降载方案下，大直径螺栓轴力变化不大，但其附加弯矩降低明显，尤其是增加关节降载方案，大直径螺栓附加弯矩降低到正常设计状态的17%，极大地提高了大直径螺栓承载能力。

表1 不同方法下大直径螺栓弯矩降低对比Tab.1 Comparison of large diameter bolt load under different states

3 试验实施

3.1 试验系统

为了获得大直径螺栓真实连接状态下承载特性，开展了静力试验，其中大直径螺栓位于舱体和过渡段之间，如图10所示。

图10 试验加载示意Fig.10 Loading diagram of test

为了测量大直径螺栓上所受的弯矩，大直径螺栓外表面周向铣出四处小平面，粘贴单向应变片，并通过结构设计增加保护罩，防止安装过程及承载过程中应变片和线缆损伤，见图11。

图11 大直径螺栓弯矩测试方案Fig.11 Schematic diagram of strain position on explosion bolt

根据大直径螺栓上的四个应变测点数据（ε1，ε2，ε3，ε4），其轴力和附加弯矩为

式中E为螺栓材料弹性模量；S为螺栓截面积；W为螺栓抗弯截面系数。

上述测试方法并非标准化的测试技术，但可以通过标定试验获得广义弹性模量，以降低相关误差。本次试验中的大直径螺栓已经过弯矩标定试验。

3.2 试验结果

试验实施过程中，进行了三次加载，第1次和第2次均为小量级加载，第3次加载至100%载荷，故大直径螺栓轴力和弯矩曲线呈现出一定的重复性。各大直径螺栓上轴力及附加弯矩变化情况见图12和图13。大直径螺栓最大轴力85 kN，最大弯矩310 N∙m。

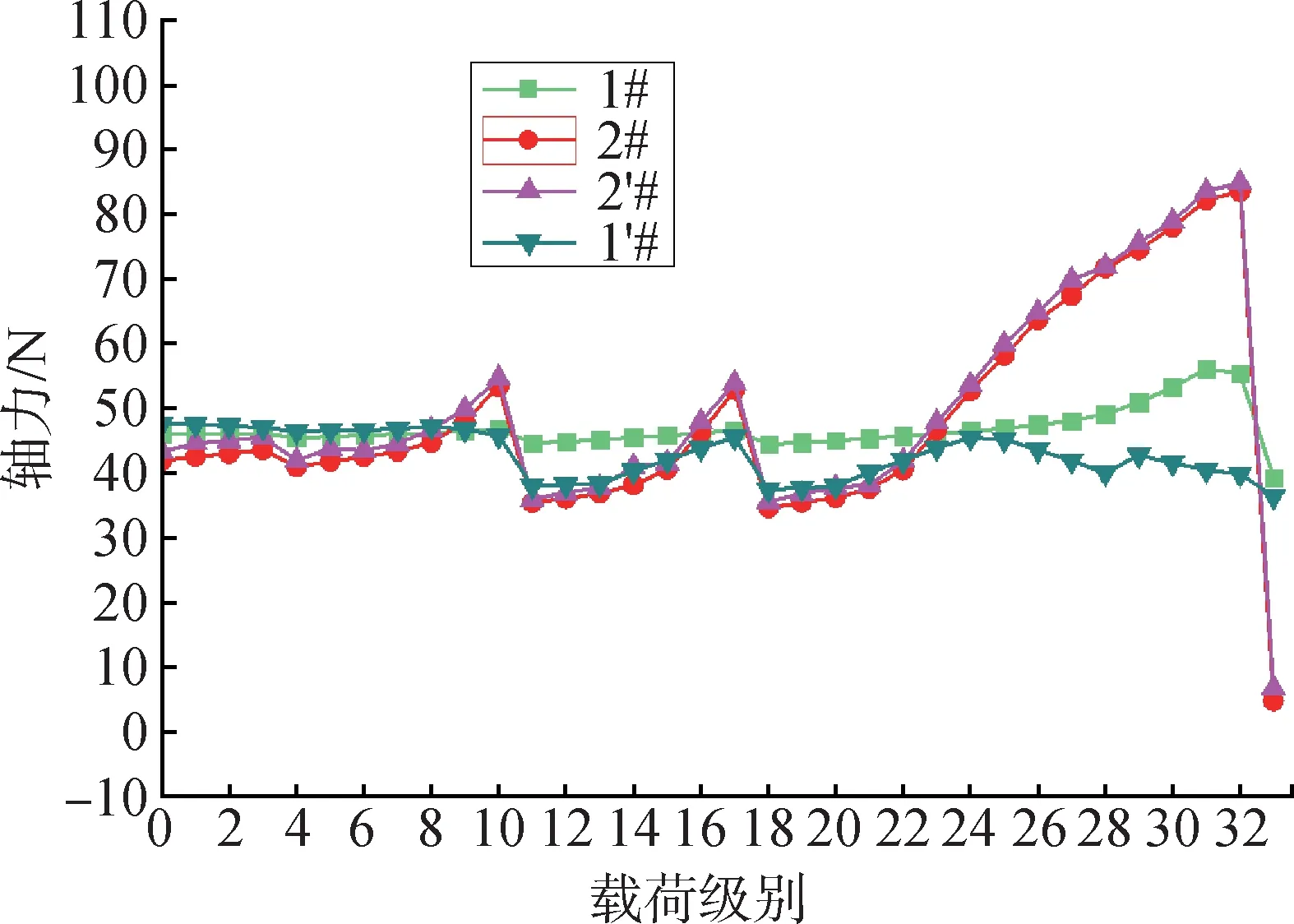
图12 试验加载过程中大直径螺栓轴力变化Fig.12 Change of axial force of large diameter bolt during test loading

图13 试验加载过程中大直径螺栓附加弯矩变化Fig.13 Change of additional bending moment of large diameter bolt during test loading

4 结果分析

4.1 拧入过程中的附加弯矩

理论来说，螺栓拧紧后，没有外部载荷，不会受到弯矩作用。但试验结果表明，施加拧紧力矩后，除轴力外，大直径螺栓也将受到90 N∙m 的弯矩作用，如图14所示。

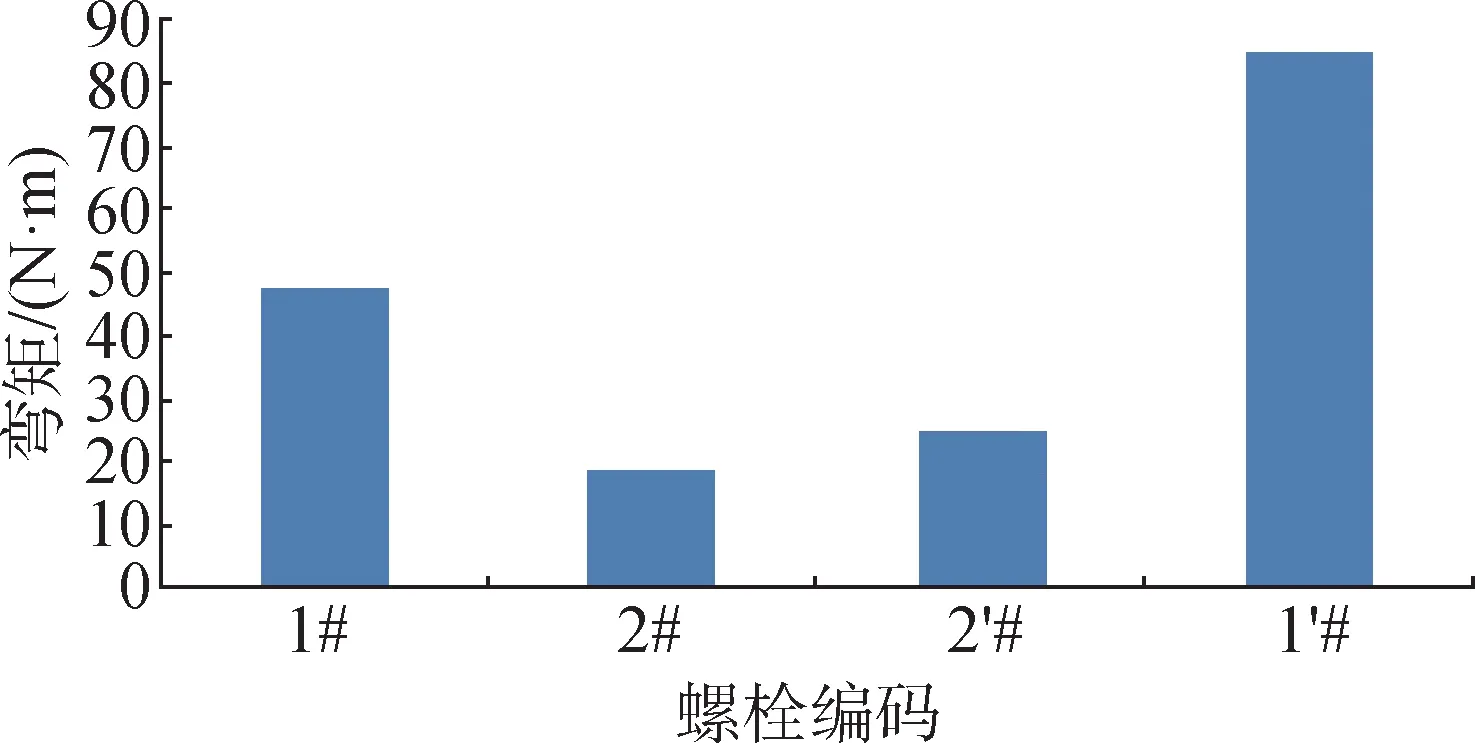
图14 大直径螺栓拧紧到位后的附加弯矩Fig.14 Secondary moments after the large diameter bolt is tightened in place

拧入过程中的附件弯矩是由大直径螺栓与安装面之间存在平行度偏差导致的。螺栓在拧紧过程中，钉头或者螺母局部与舱体结构先接触挤压，对大直径螺栓产生附加弯矩。

相同的拧紧力矩状态下，结构偏差越大，附加弯矩越大。相同的结构状态下，拧紧力矩越大，附加弯矩越大。

在结构设计过程中，对于关键连接部位，必须严格控制结构偏差，如平行度和垂直度等参数，必要时应增加螺栓强度裕度。

4.2 加载过程中的附加弯矩

试验结果表明，螺栓附加弯矩随着外载荷的增大而增大，这说明随着大直径螺栓轴力的不断增大，局部端框在载荷作用下变形逐渐加剧，轴力的不断增大和螺栓与舱体接触面积不断减小，导致螺栓附加弯矩逐渐变大。除非局部结构进入塑性变形，或者螺栓本身可适应一定的转角，降低变形不协调量，否则，随着外载荷的增大，螺栓附加弯矩的增大不可避免。

4.3 附加弯矩对承载能力的影响

按照经典材料力学公式，对于圆形结构，其弯曲应力计算公式为

式中M为圆截面所受弯矩；d为圆截面直径。

线弹性状态下，圆形结构外表面最大应力如图15所示。

图15 圆截面弯曲应力理论分布示意Fig.15 Theoretical distribution of bending stress of circular section

但实际过程中，由于材料塑性影响，结构外表面应力达到材料屈服应力后不再增长，最大应力区域逐渐从外表面向内部扩展，圆截面的实际应力分布如图16所示。

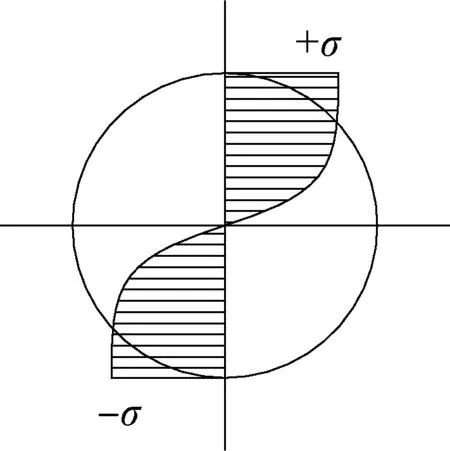
图16 圆截面弯曲应力实际分布示意Fig.16 Actual distribution of bending stress of circular section

文献［13］和文献［15］给出的螺栓强度计算公式中，均未考虑材料塑性带来的影响。文献［16］给出了不同结构在弯矩作用下的塑性修正系数，公式为

式中Sx为半个剖面对于重心（剖面中心线）的静力矩；W为抗弯截面系数；k为弯矩作用下的塑性修正系数，对于圆截面而言，k= 1.7。

故综合上述因素，考虑材料塑性影响修正后的大直径螺栓轴力为

不同状态下，获得的大直径螺栓等效轴力如表2所示。其中，第1类为工程方法分析结果，最大等效轴力为110 kN；第2类为有限元分析结果，考虑弯矩与否差别较大，其中考虑塑性修正系数后的弯矩修正状态最大等效轴力为700 kN；第3类为试验结果，考虑塑性修正系数后的弯矩修正状态最大等效轴力为380 kN。

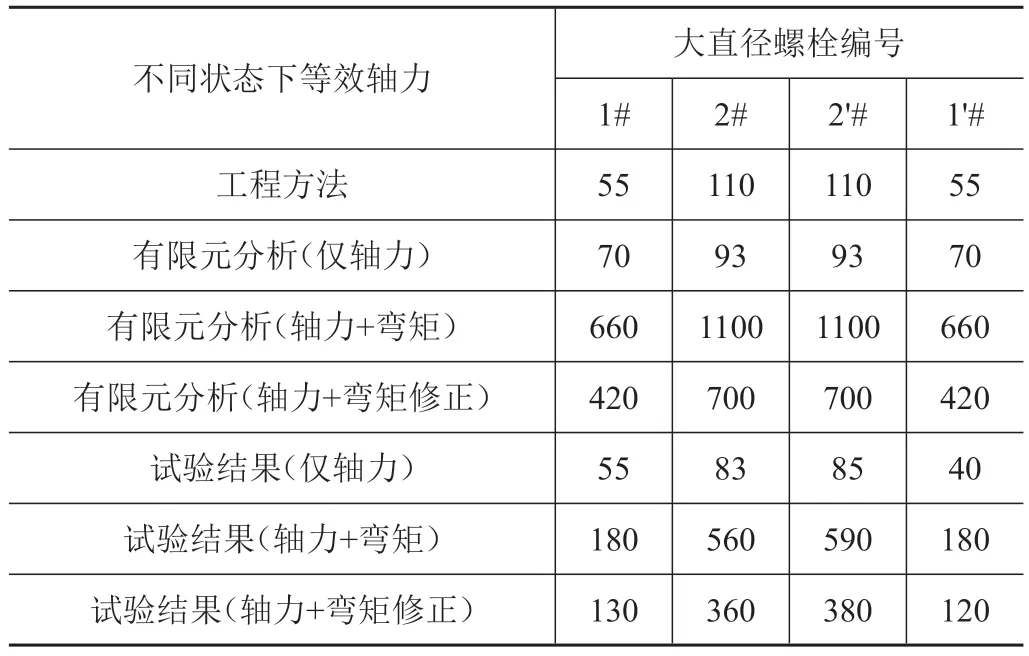
表2 不同状态下大直径螺栓等效轴力对比Tab.2 Equivalent axial force of large diameter bolt under different treatment conditions单位：kN

考虑附加弯矩影响后，其最大等效轴力约是工程方法评估结果的数倍。因此，设计过程中必须关注附加弯矩的影响，否则极有可能导致大直径因螺栓未达到设计载荷状态而提前破坏。

5 结 论

本文对某大直径螺栓典型连接结构承载特性开展了研究及试验，获得了大尺寸舱段连接状态下大直径螺栓承载特性，揭示了大直径螺栓提前破坏的原因和附加弯矩产生机理，并指出了后续优化方向，相关结论如下：

a）由于结构偏差的存在，大直径螺栓在安装过程中，便承受了一定的弯矩作用，因此应从结构设计角度降低大直径螺栓安装初始弯矩。

b）连接结构在承载过程中不可避免地存在变形，导致大直径螺栓受到附加弯矩作用，外部载荷越大，弯矩作用越明显；降低弯矩的核心是降低变形。

c）可通过塑性修正系数考虑附加弯矩对大直径螺栓承载能力的影响，提升其预示准确度和连接可靠性。

d）对比分析结果与试验结果，弯矩修正状态下，有限元分析结果约为试验结果等效轴力的两倍，存在较大偏差，有待进一步分析。

e）大直径螺栓附加弯矩产生的原因是螺栓轴力在传递过程中，局部变形导致螺栓安装面压力不均匀，故应从降低变形或者释放变形的角度降低附加弯矩，提升承载能力。

综上所述，大直径螺栓连接结构设计与分析中，必须关注附加弯矩带来的影响，否则将带来大直径螺栓提前破坏的风险。应开展头体连接联合试验及点火试验考核，按飞行时序充分验证大载荷状态下大直径螺栓结构承载功能和分离功能，避免给后续工作带来重大隐患。