基于粒子群算法的数字控制伺服系统离线参数自寻优方法研究

杨弘枨，刘 山，许文波，张 博，李沛文

（北京精密机电控制设备研究所，北京，100076）

0 引 言

目前，航天伺服领域已经广泛采用了数字控制器和数字控制算法，为提高伺服系统性能提供了便利的手段。当前大多采用以传递函数为基础的经典控制理论对系统性能进行设计和校正。其中，机电伺服系统产品由于采用全数字控制，特性较为一致，控制参数在经过设计阶段调试后一般可固化在控制算法中，生产过程中不需要更改。而电液伺服系统使用的伺服阀受到机加尺寸、装配等环节影响，导致合格产品的静、动态特性存在一定散布，有时需要对软件中的控制参数进行调整，保证系统性能满足控制系统任务书指标要求。

粒子群算法是由Kennedy 和Eberhart 等于1995 年提出的一种演化计算算法［1-2］，该方法对初值选取具有一定的鲁棒性，收敛速度快，全局收敛性较好，是一种适用于工程应用的参数寻优方法［3］。目前粒子群算法已广泛应用于函数优化、神经网络训练和模糊系统控制等领域。本文将其应用于数字伺服系统控制参数的离线寻优，开展了相关理论分析和仿真研究。

1 推力矢量控制伺服系统特性校正原理

某电液伺服系统的控制原理如图1所示，使用PⅠ控制方法，结合滤波环节进行频率特性幅值和相位的调整，其中有多项控制参数需要进行整定。

图1 电液伺服系统控制原理Fig.1 Control principle of electro-hydraulic servo system

由于伺服阀的静、动态特性存在一定散布，为补偿伺服阀的性能差异，确保电液伺服系统的频率特性在满足任务书指标要求的同时具有一定余量，通常由设计人员手动调试数字控制器内的相关参数，不适用于后续大批量生产，因此，需要对伺服系统控制参数自整定方法进行研究，提高调试速度和产品合格率。

2 粒子群算法

粒子群算法通过模拟鸟群觅食过程中的迁徙和聚集，产生不可预测的群体搜索行为。在优化之前首先执行初始化：在给定的解空间内对粒子群赋予一组随机值。给定的解空间决定了优化的速度，对粒子群进行随机赋值的目的是在全局范围内搜寻目标问题的最优解，确保了最优解的求解精度。个体粒子有了初始值等其他属性后，将其代入优化目标函数进行适应度的计算。然后通过迭代寻优。迭代过程即持续更新与寻优的过程。在每一次迭代中，每个粒子通过跟踪个体最优值Pbest（个体粒子本身在迭代过程中找寻到的最优解粒子）和全局最优值Gbest（种群中所有的粒子们在迭代过程中所找寻到的最优解）来更新自己在解空间内的位置与飞行速度。

与人工控制参数整定方法相比，将粒子群算法用于伺服系统控制器参数自整定主要有以下优点：a）可同时对多项控制参数整定，比人工逐个调试各项参数的方法效率更高；b）可对大量控制参数自动进行计算，寻优范围更广，优化度更高；c）可根据实际需求自主设计算法的目标函数；d）可在指定范围内进行参数寻优，使整定结果能够保证系统的稳定性。

3 基于粒子群算法的伺服系统离线参数自寻优方法

本节结合电液伺服系统调试过程，分别确定粒子群算法的适应度函数、粒子编码方式、参数搜索空间、粒子学习速度和算法规模，设计了一种基于粒子群算法的电液伺服系统离线参数自寻优方法。

3.1 适应度函数的设计

首先，根据控制系统任务书和人工调试结果确定寻优目标特性，即适应度函数。

对于同一伺服作动器，如果忽略泄露对其性能的影响，可以认为从伺服阀流量到作动器位移的传递特性GxQ不变，因此影响伺服系统性能的主要因素为控制偏差e到伺服阀流量Q的传递特性GQe。若能得到比较一致的传递特性GQe，即可保证伺服系统总体性能的一致性。由于伺服阀流量特性难以通过测量获取，因此将传递特性GQe按照式（1）进行计算：

式中N为控制网络的传递特性；Gxδ为指令信号到线位移的传递特性；Giδ为阀电流到线位移的传递特性。Gxδ和Giδ均可通过对测试数据进行分析获得。

为得到稳定一致的GQe，则需Gxδ/GiδN在不同性能伺服阀条件下能够保持一致。而对于固定的伺服阀和作动器，阀电流到作动器输出线位移的传递特性通常保持不变，即Gxδ/Giδ频率特性不变，且可通过对测试数据进行分析获得。因此可以结合Gxδ/Giδ测试特性，计算得到需要的目标网络特性N̂，使Gxδ/GiδN特性保持一致。

使用粒子群算法对电液伺服系统进行整定时，需要建立单一的、能反映控制系统综合性能的指标。本文以人工调试完成、性能较好的伺服系统的Gxδ/GiδN特性作为整定目标。参数寻优前，首先进行一次初测，得到待调试系统的阀电流到作动器输出线位移的Gxδ/Giδ频率特性，然后可通过计算解得所需要的控制网络目标特性N̂，将其作为适应度的计算准则。

粒子适应度的计算方法为：粒子当前位置值对应一组控制参数，计算按照该组控制参数设置的控制网络频率特性与目标网络特性N̂在各测试频率点幅值特性的方差并求和取倒数。

适应度F的计算公式为

式中M0(ωi)为控制网络目标频率特性在第i个频率点的幅值；P0(ωi)为控制网络目标频率特性在第i个频率点的相位，共有m个频率点；MN(ωi)为待评估的粒子位置代表的控制参数代入控制网络时在相应频率点的幅值；PN(ωi)为待评估的粒子位置代表的控制参数代入控制网络时在相应频率点的相位；ηM为幅值权值；ηP为相位权值。用粒子适应度描述粒子位置值对应的控制参数与能达到目标特性控制参数的接近程度，可以用该指标反映控制系统综合性能。

3.2 粒子编码方式和参数搜索空间

根据控制器可装订参数确定粒子编码方式和参数搜索空间。伺服系统需要整定的控制参数包括控制器位置增益KP、积分增益KⅠ、陷波频率w0、滤波器wf、滤波器阻尼ξ0及ξf，因此将粒子的解空间维数设为六维，位置编码方式定义为［KP，KⅠ，w0，wf，ξ0，ξf］。为保证参数整定结果的稳定性，需要使粒子群在规定的控制参数范围内进行整定。基于伺服系统稳定性分析结果和批产工艺数据包络，确定参数寻优范围为［0.7，1；0.2，0.25；100，200；0.01，1；100，200；0.01，1］。这是对电液伺服系统进行多次调试后总结出的控制参数范围，并适当进行扩大，尝试找到比历史经验更优的控制参数组合。

3.3 控制参数自整定方法

基于粒子群算法的电液伺服系统控制参数自整定具体步骤如下：

a）初始化粒子群信息。首先设置种群个数为200，迭代次数为100，惯性权重w为0.8，自我学习速度c1为0.5，群体学习速度c2为0.5。随机产生各粒子的初始位置。

b）个体粒子有了初始位置后，计算每个粒子的适应度，适应度F按照式（2）进行计算。

c）分别记录每个粒子的适应度，记录每个粒子个体的历史最佳位置xm和历史最佳适应度fxm，并更新群体最佳位置ym和群体最佳适应度fym。

d）更新每个粒子的速度，其中，每个粒子速度的方向将朝着个体最优值和群体最优值的方向进行跟踪，体现了粒子群算法的进化属性，使得粒子群整体朝着全局最优点逐渐运动。粒子的速度更新公式为

式中 rand1，rand2为0～1之间的随机值。

位置更新公式为

e）根据粒子更新后的位置，重复步骤b，计算新位置的适应度，并更新个体的历史最佳位置xm、历史最佳适应度fxm、群体最佳位置ym和群体最佳适应度fym。

f）达到最大迭代次数时，或多次运算后群体最佳适应度保持不变，或在搜寻到满足要求的最佳位置时，终止计算。

基于粒子群算法的伺服系统控制参数自整定方法流程如图2所示。

图2 基于粒子群算法的伺服系统控制参数自整定流程Fig.2 Self-tuning process of servo system control parameters based on particle swarm optimization algorithm

4 整定实例

使用上述方法，对某电液伺服系统的一套伺服作动器进行参数自整定。

根据对该伺服作动器实测数据的分析，计算得到所需的控制网络目标特性如图3所示。

图3 控制网络目标特性Fig.3 Target characteristics of control network

运行粒子群算法，并改变运算规模进行多次仿真验证，参数自整定结果如表1所示。

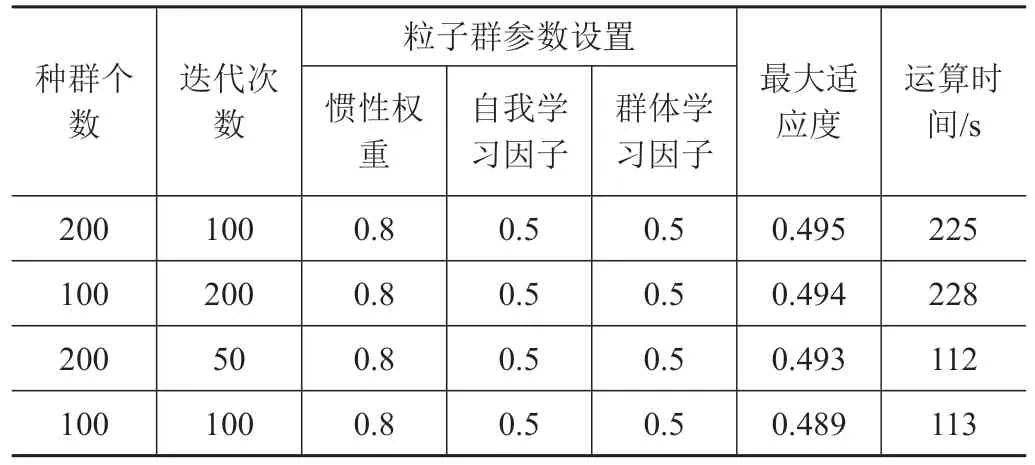
表1 粒子群算法参数自整定结果Tab.1 Parameter self tuning results of particle swarm optimization

由表1可知，基于粒子群算法的控制参数自整定方法可以在225 s 左右找到全局最优值。多次计算结果接近，证明该方法对初值选取具有一定的鲁棒性，全局收敛性较好；且减小运算规模后，运算112 s 即已接近全局最优值，算法收敛较快。

适应度最大时的最优控制参数组合为KP=0.849，KⅠ=0.2，w0=158.047，ζ0=0.120，wf=194.413，ζf=0.311。

将粒子群算法求得的最优参数组合作为控制网络的各项参数，控制网络的频率特性和目标网络特性对比如图4所示。

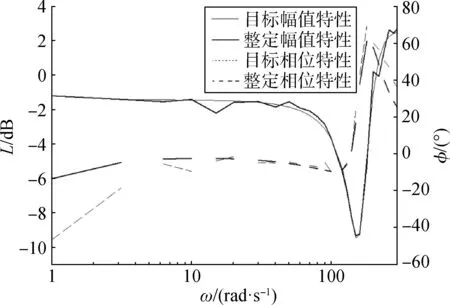
图4 控制网络的频率特性和目标特性对比Fig.4 Comparison of frequency characteristics and target characteristics of control network

整定后伺服系统的闭环频率特性如图5所示。

图5 自整定后伺服系统的闭环频率特性Fig.5 Closed loop frequency characteristics of servo system after self-tuning

由图5可以看出，由粒子群算法整定后伺服系统的闭环频率特性能够满足任务书要求，且余量充足。因此，通过基于粒子群算法的伺服系统控制参数自整定方法整定得到的控制参数组合可以对伺服阀的差异进行补偿，使伺服阀性能具有差异的伺服系统传递特性GQe保持不变，在伺服阀小信号流量特性发生一定散布的情况下，保证伺服系统性能满足任务书指标要求。

5 结束语

根据以上研究可知，将粒子群算法应用于对某电液伺服系统的控制参数自整定，可以实现数字伺服系统控制参数离线寻优的自动化。同时，使用粒子群算法得到的控制网络频率特性与能够补偿伺服阀特性散布的目标特性非常接近。仿真结果表明，该参数自寻优方法能同时对多项控制参数寻优，可大量节省人工调试时间，优化人工整定的繁琐过程，具有更高的调试效率，能够在保证系统稳定性的同时在更广范围内找到最符合实际需求的控制参数。